scipy笔记:scipy.interpolate.interp1d
1 主要使用方法
class scipy.interpolate.interp1d(x, y, kind='linear', axis=-1, copy=True, bounds_error=None, fill_value=nan, assume_sorted=False)2 主要函数
| x | 一维实数值数组,代表插值的自变量 | ||||||||||||||||
| y | N维实数值数组,其中沿着插值轴的 y 长度必须等于 x 的长度 默认的插值轴是 y 的最后一个轴 | ||||||||||||||||
| kind | str or int 指定插值类型的字符串或表示样条插值器阶数的整数 指定的插值类型有:
| ||||||||||||||||
| axis | y 数组中对应于 x 坐标值的轴。默认值为 -1。 | ||||||||||||||||
| copy | 若为 True,则该类会对 x 和 y 进行内部复制。若为 False,则使用 x 和 y 的引用。默认为 True | ||||||||||||||||
| bounds_error | 若为 True,在 x 范围外进行插值尝试时(需要外推)会引发 ValueError。 若为 False,则超出范围的值会被赋予 fill_value。 默认情况下,除非指定 fill_value="extrapolate",否则会引发错误 | ||||||||||||||||
| fill_value | 如果为 ndarray(或浮点数),则在数据范围外的请求点将使用此值填充。 如果未提供,则默认为 NaN。 如果为两元素元组,则第一个元素用于 x_new < x[0],第二个元素用于 x_new > x[-1]。 使用两元素元组或 ndarray 需要 bounds_error=False | ||||||||||||||||
| assume_sorted | 如果为 False,x 的值可以任意排序,并且首先进行排序。 如果为 True,则 x 必须是单调递增的数组 |
3 举例
3.1 导入库&准备数据
# 导入库
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import *# 数据部分
x=np.arange(0,10)
y=np.exp(-x/3.0)3.2 创建interp1d
x_new=np.arange(0,9,0.1)
y_new=f(x_new)
y_new
'''
array([1. , 0.97165313, 0.94330626, 0.91495939, 0.88661252,0.85826566, 0.82991879, 0.80157192, 0.77322505, 0.74487818,0.71653131, 0.69621989, 0.67590847, 0.65559705, 0.63528563,0.61497421, 0.5946628 , 0.57435138, 0.55403996, 0.53372854,0.51341712, 0.49886335, 0.48430958, 0.46975582, 0.45520205,0.44064828, 0.42609451, 0.41154074, 0.39698698, 0.38243321,0.36787944, 0.35745121, 0.34702298, 0.33659475, 0.32616652,0.31573829, 0.30531006, 0.29488183, 0.2844536 , 0.27402537,0.26359714, 0.25612498, 0.24865283, 0.24118068, 0.23370852,0.22623637, 0.21876422, 0.21129206, 0.20381991, 0.19634776,0.1888756 , 0.18352157, 0.17816754, 0.17281351, 0.16745947,0.16210544, 0.15675141, 0.15139738, 0.14604335, 0.14068932,0.13533528, 0.13149895, 0.12766262, 0.12382629, 0.11998996,0.11615363, 0.11231729, 0.10848096, 0.10464463, 0.1008083 ,0.09697197, 0.09422312, 0.09147426, 0.08872541, 0.08597656,0.08322771, 0.08047886, 0.07773001, 0.07498115, 0.0722323 ,0.06948345, 0.06751381, 0.06554417, 0.06357454, 0.0616049 ,0.05963526, 0.05766562, 0.05569598, 0.05372634, 0.05175671])
'''plt.plot(x,y,'o',x_new,y_new,'-')
3.3 不同kind不同结果
f_c=interp1d(x,y,kind='previous')
y_new=f_c(x_new)
plt.plot(x,y,'o',x_new,y_new,'-')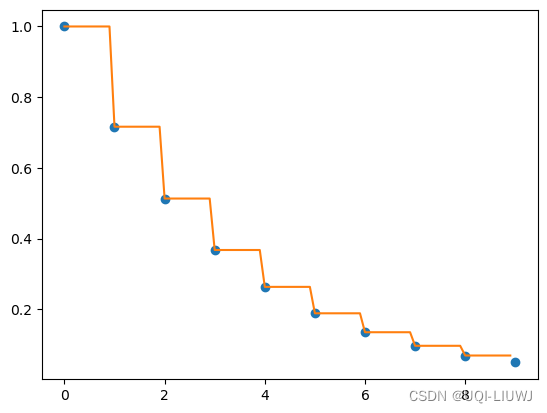
相关文章:

scipy笔记:scipy.interpolate.interp1d
1 主要使用方法 class scipy.interpolate.interp1d(x, y, kindlinear, axis-1, copyTrue, bounds_errorNone, fill_valuenan, assume_sortedFalse) 2 主要函数 x一维实数值数组,代表插值的自变量y N维实数值数组,其中沿着插值轴的 y 长度必须等于 x 的…...

外包干了一个月,技术明显进步。。。。。
先说一下自己的情况,本科生生,19年通过校招进入南京某软件公司,干了接近2年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了2年的功能测试…...

docker安装node及使用
文章目录 一、安装node二、创建node容器三、进入创建的容器如有启发,可点赞收藏哟~ 一、安装node 查看可用版本 docker search node安装最新版本 docker install node:latest二、创建node容器 docker run -itd --name node-test node–name node-test࿱…...

要求CHATGPT高质量回答的艺术:提示工程技术的完整指南—第 18 章:对抗性提示
要求CHATGPT高质量回答的艺术:提示工程技术的完整指南—第 18 章:对抗性提示 对抗性提示是一种允许模型生成能够抵御某些类型的攻击或偏差的文本的技术。这种技术可用于训练更健壮、更能抵御某些类型的攻击或偏差的模型。 要在 ChatGPT 中使用对抗性提…...

若依框架的搭建
若依框架 若依框架的搭建(前后端分离版本)环境要求IDEA拉取Gitee源码Mysql 配置Redis 配置后端启动前端配置问题解决 效果展示 若依框架的搭建(前后端分离版本) 简介 RuoYi-Vue 是一个 Java EE 企业级快速开发平台,基…...
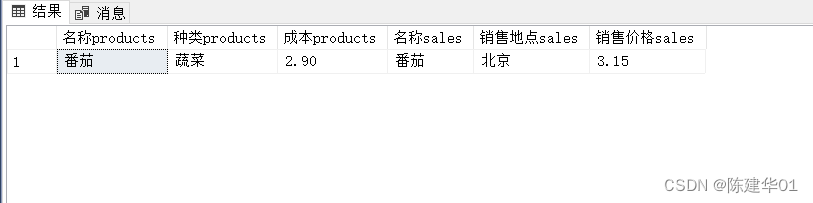
SQL Server 数据库,多表查询
4.2使用T-SQL实现多表查询 前面讲述过的所有查询都是基于单个数据库表的查询,如果一个查询需要对多个表进行操作, 就称为联接查询,联接查询的结果集或结果称为表之间的联接。 联接查询实际上是通过各个表之间共同列的关联性来查询数据的&…...

程序解释与编译
▶1.程序的解释执行方式 程序语言强写的计策机指令序列称为“源程序”,计算机并不能直接执行用高级语言编写的源程序,源程序必须通过“翻译程序”翻译成机器指令的形式,计算机才能项别和执行。源程序的翻译有两种方式:解释执行和编译执行。不…...

聊聊 Jetpack Compose 的 “状态订阅自动刷新” -- mutableStateListOf
Jekpack Compose “状态订阅&自动刷新” 系列: 【 聊聊 Jetpack Compose 的 “状态订阅&自动刷新” - - MutableState/mutableStateOf 】 【 聊聊 Jetpack Compose 的 “状态订阅&自动刷新” - - remember 和重组作用域 】 【 聊聊 Jetpack Compose 的 …...

Dockerfile详解#如何编写自己的Dockerfile
文章目录 前言编写规则指令详解FROM:基础镜像LABEL:镜像描述信息MAINTAINER:添加作者信息COPY:从宿主机复制文件到镜像中ADD:从宿主机复制文件到镜像中WORKDIR:设置工作目录 前言 Dockerfile是编写docker镜…...

Elasticsearch桶聚合和管道聚合
1. 根据名称统计数量 GET order/_search {"_source": false,"aggs": {"aggs_name": { // 自定义查询结果名称"terms": { // 使用的函数"field": "name.keyword"}}} }查询结果例子: "aggregat…...

联想范建平:联想混合AI架构具备两大明显优势
12月7日,首届AI PC创新论坛在北京联想集团总部举办。联想集团副总裁、联想研究院人工智能实验室负责人范建平表示,为提供真正可信、个性化的AI专属服务,联想提出了混合智能(Hybrid AI)概念,并已经显现出更强…...

探索Spring事件监听机制的奇妙世界
文章目录 什么是Spring事件监听机制主要组件内置的事件监听类自定义事件监听类总结 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 什么是Spring事件监听机制 Spring事件监听机制是Spr…...

什么是散列函数
散列函数是一种公开的数学函数。散列函数运算的输入信息也可叫作报文。散列函数运算后所得到的结果叫作散列码或者叫作消息摘要。散列函数具有如下一些特点: (1)不同内容的报文具有不同的散列码,而一旦原始报文有任何改变…...

tomcat反序列化
漏洞介绍: 漏洞名称: Apache Tomcat反序列化漏洞影响范围: Apache Tomcat服务器中使用了自带session同步功能的配置,且没有使用Encrypt Interceptor加密拦截器的情况下。漏洞描述: Apache Tomcat是一个基于Java的Web应用软件容器,用于运行servlet和JSP Web应用。当Tomc…...

flask 请求勾子实现 request_auth认证
from flask import g,request from comment.utils.tokens_pyjwt import verify_tokensdef jwt_request_auth():从请求(request)中获取token,并且验证token,验证成功之后把用户id保存到全局变量g中g.user_idNone #定义变量#前端代码是是把token携带请求头…...

【STM32入门】3.OLED屏幕
1.OLED引脚 OLED屏幕的接线按图所示,本例中用的是4管脚OLED屏幕 2.驱动程序 配套的驱动程序是“OLED.c",主要由以下函数构成:1、初始化;2、清屏;3、显示字符;4、显示字符串;5、显示数字…...

python圣诞树代码编程
以下是一个简单的Python圣诞树代码: def draw_tree(height): for i in range(height): print( * (height - i - 1) * * (2 * i 1)) print( * (height - 1) |)draw_tree(10) 这个函数会绘制一个等腰三角形,其中每一行的星号数量从1开…...
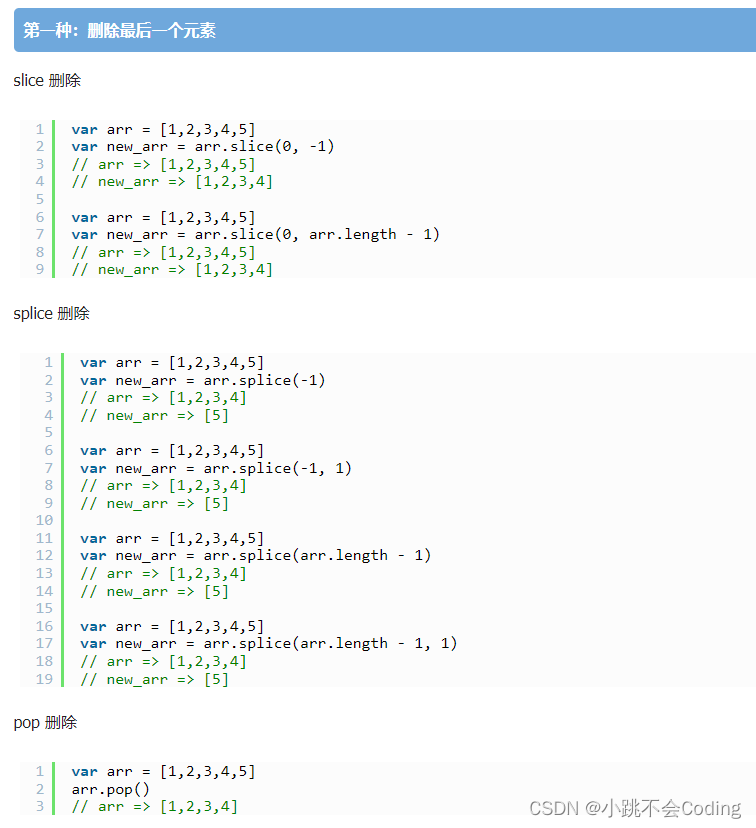
js数组删除某个元素
...
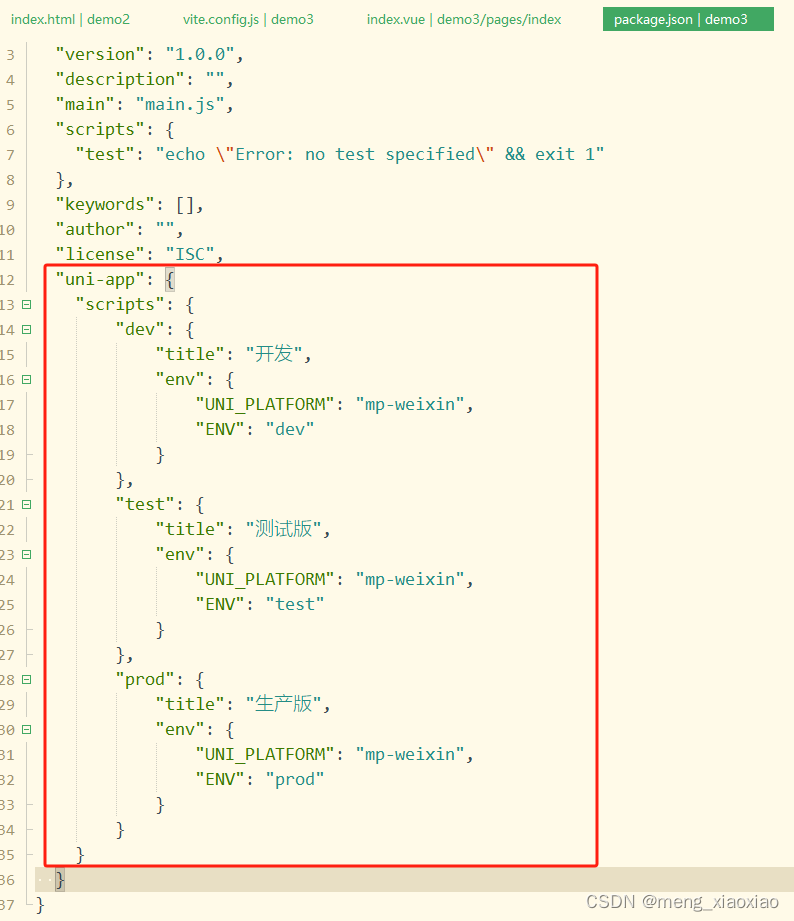
hbuilder + uniapp +vue3 开发微信云小程序
1、创建项目: 2、创建项目完成的默认目录结构: 3、在根目录新建一个文件夹cloudFns(文件名字随便),存放云函数源码: 4、修改manifest.json文件:添加 小程序 appid和cloudfunctionRoot࿰…...

服务器配置免密SSH
在当今互联网时代,远程工作和网络安全已成为信息技术领域的热点话题。无论是管理远程服务器、维护网络设备还是简单地从家中连接到办公室,安全始终是首要考虑的因素。这就是为什么 SSH(Secure Shell)成为了网络专业人士的首选工具…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...
