【CSP】202209-1_如此编码Python实现
文章目录
- @[toc]
- 试题编号
- 试题名称
- 时间限制
- 内存限制
- 题目背景
- 题目描述
- 输入格式
- 输出格式
- 样例1输入
- 样例1输出
- 样例2输入
- 样例2输出
- 样例3输入
- 样例3输出
- 样例3解释
- 子任务
- 提示
- `Python`实现
文章目录
- @[toc]
- 试题编号
- 试题名称
- 时间限制
- 内存限制
- 题目背景
- 题目描述
- 输入格式
- 输出格式
- 样例1输入
- 样例1输出
- 样例2输入
- 样例2输出
- 样例3输入
- 样例3输出
- 样例3解释
- 子任务
- 提示
- `Python`实现
试题编号
试题名称
时间限制
内存限制
题目背景
- 某次测验后,顿顿老师在黑板上留下了一串数字 23333 23333 23333便飘然而去,凝望着这个神秘数字,小 P P P同学不禁陷入了沉思
题目描述
- 已知某次测验包含 n n n道单项选择题,其中第 i i i题 ( 1 ≤ i ≤ n ) (1 \leq i \leq n) (1≤i≤n)有 a i a_{i} ai个选项,正确选项为 b i b_{i} bi,满足 a i ≥ 2 a_{i} \geq 2 ai≥2且 0 ≤ b i < a i 0 \leq b_{i} < a_{i} 0≤bi<ai
- 比如说, a i = 4 a_{i} = 4 ai=4表示第 i i i题有 4 4 4个选项,此时正确选项 b i b_{i} bi的取值一定是 0 0 0、 1 1 1、 2 2 2、 3 3 3其中之一
- 顿顿老师设计了如下方式对正确答案进行编码,使得仅用一个整数 m m m便可表示 b 1 b_{1} b1, b 2 b_{2} b2, ⋯ \cdots ⋯, b n b_{n} bn
- 首先定义一个辅助数组 c i c_{i} ci,表示数组 a i a_{i} ai的前缀乘积,当 1 ≤ i ≤ n 1 \leq i \leq n 1≤i≤n时,满足:
c i = a 1 × a 2 × ⋯ × a i c_{i} = a_{1} \times a_{2} \times \cdots \times a_{i} ci=a1×a2×⋯×ai
- 特别地,定义 c 0 = 1 c_{0} = 1 c0=1
- 于是 m m m便可按照如下公式算出
m = ∑ i = 1 n c i − 1 × b i = c 0 × b 1 + c 1 × b 2 + ⋯ + c n − 1 × b n \begin{aligned} m &= \displaystyle\sum\limits_{i = 1}^{n}{c_{i - 1} \times b_{i}} \\ &= c_{0} \times b_{1} + c_{1} \times b_{2} + \cdots + c_{n - 1} \times b_{n} \end{aligned} m=i=1∑nci−1×bi=c0×b1+c1×b2+⋯+cn−1×bn
- 易知, 0 ≤ m < c n 0 \leq m < c_{n} 0≤m<cn,最小值和最大值分别当 b i b_{i} bi全部为 0 0 0和 b i = a i − 1 b_{i} = a_{i} - 1 bi=ai−1时取得
- 试帮助小 P P P同学,把测验的正确答案 b 1 b_{1} b1, b 2 b_{2} b2, ⋯ \cdots ⋯, b n b_{n} bn从顿顿老师留下的神秘整数 m m m中恢复出来
输入格式
- 从标准输入读入数据
- 输入共两行
- 第一行包含用空格分隔的两个整数 n n n和 m m m,分别表示题目数量和顿顿老师的神秘数字
- 第二行包含用空格分隔的 n n n个整数 a 1 a_{1} a1, a 2 a_{2} a2, ⋯ \cdots ⋯, a n a_{n} an,依次表示每道选择题的选项数目
输出格式
- 输出到标准输出
- 输出仅一行,包含用空格分隔的 n n n个整数 b 1 b_{1} b1, b 2 b_{2} b2, ⋯ \cdots ⋯, b n b_{n} bn,依次表示每道选择题的正确选项
样例1输入
15 32767
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
样例1输出
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
样例2输入
4 0
2 3 2 5
样例2输出
0 0 0 0
样例3输入
7 23333
3 5 20 10 4 3 10
样例3输出
2 2 15 7 3 1 0
样例3解释
| i i i | 1 1 1 | 2 2 2 | 3 3 3 | 4 4 4 | 5 5 5 | 6 6 6 | 7 7 7 |
|---|---|---|---|---|---|---|---|
| a i a_{i} ai | 3 3 3 | 5 5 5 | 20 20 20 | 10 10 10 | 4 4 4 | 3 3 3 | 10 10 10 |
| b i b_{i} bi | 2 2 2 | 2 2 2 | 15 15 15 | 7 7 7 | 3 3 3 | 1 1 1 | 0 0 0 |
| c i − 1 c_{i - 1} ci−1 | 1 1 1 | 3 3 3 | 15 15 15 | 300 300 300 | 3000 3000 3000 | 12000 12000 12000 | 36000 36000 36000 |
子任务
- 50 % 50\% 50%的测试数据满足: a i a_{i} ai全部等于 2 2 2,即每道题均只有两个选项,此时 c i = 2 i c_{i} = 2^{i} ci=2i
- 全部的测试数据满足: 1 ≤ n ≤ 20 1 \leq n \leq 20 1≤n≤20, a i ≥ 2 a_{i} \geq 2 ai≥2且 c n ≤ 1 0 9 c_{n} \leq 10^{9} cn≤109(根据题目描述中的定义 c n c_{n} cn表示全部 a i a_{i} ai的乘积)
提示
- 对任意的 1 ≤ j ≤ n 1 \leq j \leq n 1≤j≤n,因为 c j + 1 c_{j + 1} cj+1, c j + 2 c_{j + 2} cj+2, ⋯ \cdots ⋯均为 c j c_{j} cj的倍数,所以 m m m除以 c j c_{j} cj的余数具有如下性质:
m % c j = ∑ i = 1 j c i − 1 × b i m \% c_{j} = \displaystyle\sum\limits_{i = 1}^{j}{c_{i - 1} \times b_{i}} m%cj=i=1∑jci−1×bi
- 其中 % \% %表示取余运算,令 j j j取不同的值,则有如下等式:
m % c 1 = c 0 × b 1 m % c 2 = c 0 × b 1 + c 1 × b 2 m % c 2 = c 0 × b 1 + c 1 × b 2 + c 2 × b 3 \begin{aligned} m \% c_{1} &= c_{0} \times b_{1} \\ m \% c_{2} &= c_{0} \times b_{1} + c_{1} \times b_{2} \\ m \% c_{2} &= c_{0} \times b_{1} + c_{1} \times b_{2} + c_{2} \times b_{3} \end{aligned} m%c1m%c2m%c2=c0×b1=c0×b1+c1×b2=c0×b1+c1×b2+c2×b3
Python实现
n, m = map(int, input().split())
a = list(map(int, input().split()))b = []
c = 1for i in range(n):temp = cc *= a[i]b.append((m % c) // temp)print(*b)
相关文章:

【CSP】202209-1_如此编码Python实现
文章目录 [toc]试题编号试题名称时间限制内存限制题目背景题目描述输入格式输出格式样例1输入样例1输出样例2输入样例2输出样例3输入样例3输出样例3解释子任务提示Python实现 试题编号 202209-1 试题名称 如此编码 时间限制 1.0s 内存限制 512.0MB 题目背景 某次测验后&#x…...

std::function
通过使用std::function,可以将不同类型的可调用对象封装成统一的格式,从而使用相同的接口进行调用;在设计回掉函数、事件处理 、函数对象等场景中十分有用。 ① 封装函数指针 ② 封装lambda ③ 封装成员函数等 1. 包含头文件 #include<fun…...

SQL Server——权限管理
一。SQL Server的安全机制 SQL Server 的安全性是建立在认证和访问许可两种安全机制之上的。其中.认证用来确定登录Sal Server 的用户的登录账户和密码是否正确.以此来验证其是否具有连接SQL Server 的权限;访问许可用来授予用户或组能够在数据库中执行哪…...
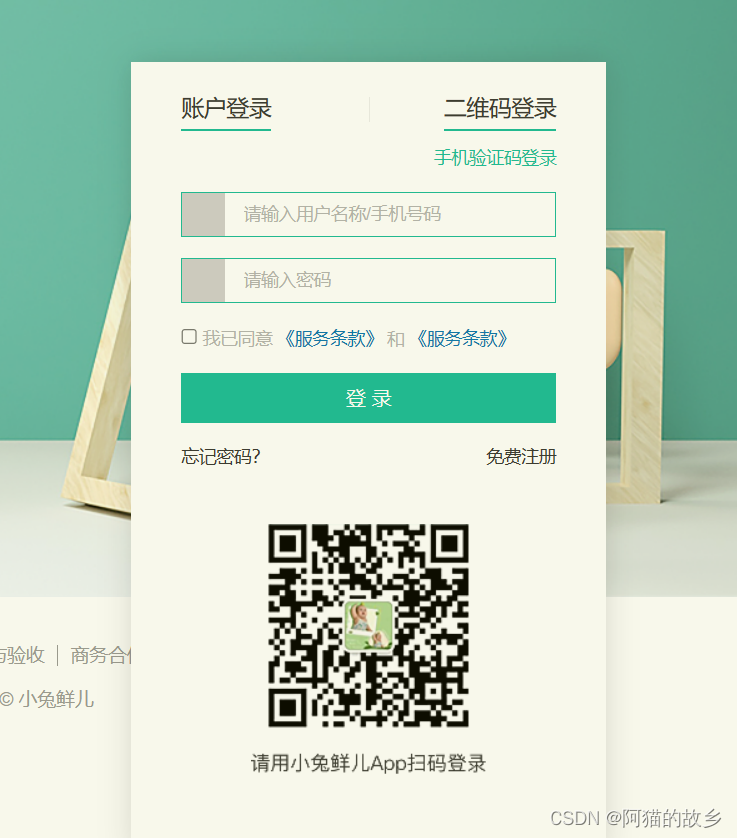
实例解析关于兔鲜登录tab栏切换案例详细讲解!
文章目录 文章目录 效果图展示 整体制作的一个思路 代码展示 技术细节 小结 效果图展示 点击账户登录显示登录的模块,点击二维码登录显示二维码的模块 整体制作的一个思路 点击哪个模块哪个显示,另外一个模块让它隐藏即可! 代码展示 <!…...

制作一个RISC-V的操作系统三-编译与链接
文章目录 GCCGCC简介GCC的命令格式gcc -Egcc -cgcc -Sgcc -ggcc -vGCC的主要执行步骤GCC涉及的文件类型针对多个源文件的处理 ELFELF介绍ELF文件格式ELF文件处理相关工具:Binutils(binary utility)readlelf -hreadelf -S或readelf -SW&#x…...

tmux工具--程序部署在服务器上持久化执行
程序部署在服务器上,想持久化执行 做以下操作: 在服务器上安装 tmux工具 对于 Ubuntu 或 Debian: sudo apt-get install tmux对于 CentOS 或 RHEL: sudo yum install tmux对于 Fedora: sudo dnf install tmux对于…...
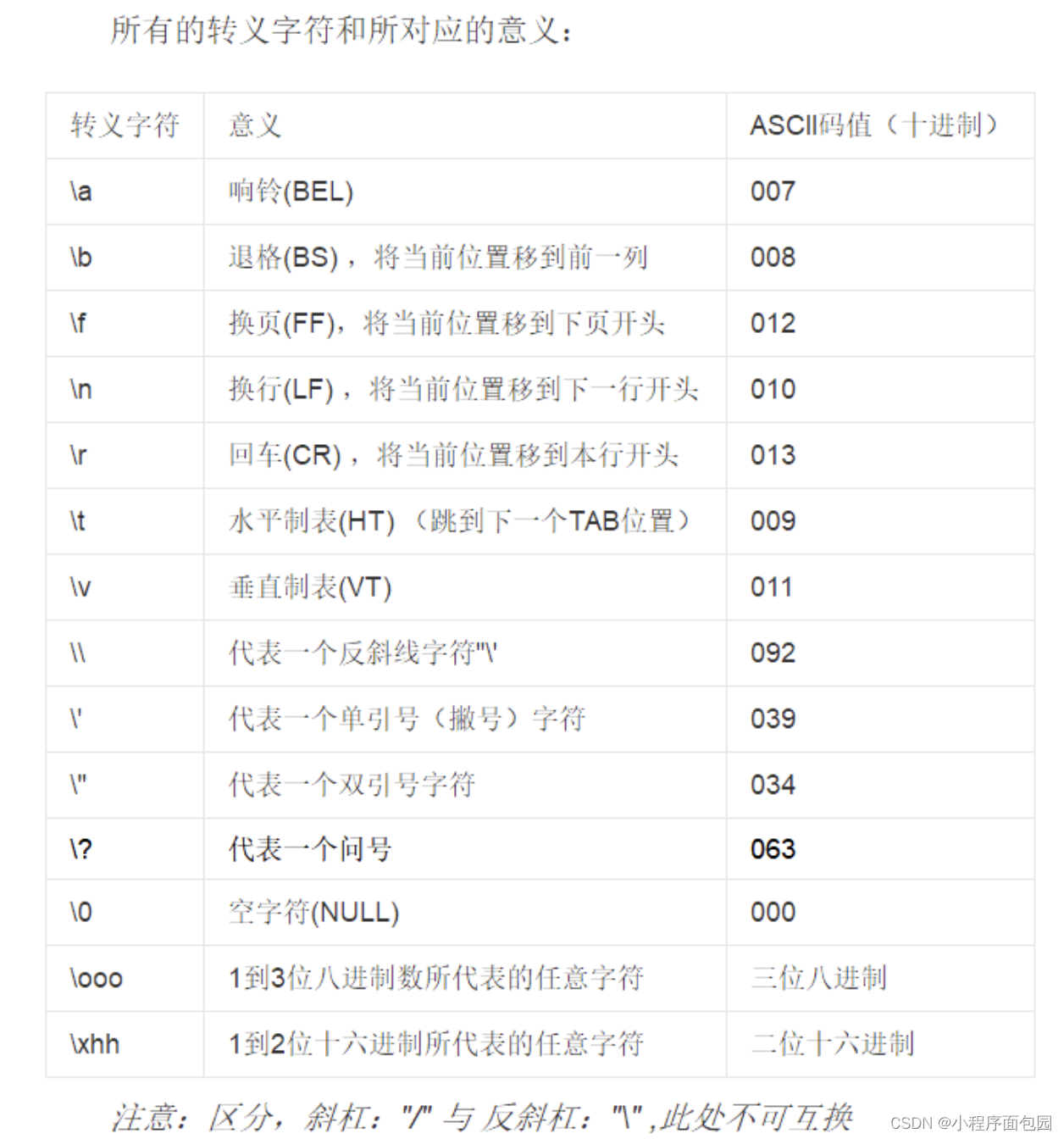
C语言精选——选择题Day39
第一题 1. 有下面的定义,则 sizeof(s) 为多少? char *s "\ta\017bc"; A:9 B:5 C:6 D:7 答案及解析 C 本题涉及到了转义字符 \t 是水平制表符,算一个字节 \017 是表示八进制数&#…...
React 笔记 jsx
严格约定:React 组件必须以大写字母开头,而 HTML 标签则必须是小写字母。 React JSX JSX 是由 React 推广的 JavaScript 语法扩展。 用于表达组件的 特殊语法的 js 函数 要求标签必须闭合;返回的组件必须包裹在一个父标签内; …...

QMenu风格设计qss+阴影
Qt的菜单经常在软件开发中用到,默认的菜单效果都不符合设计师的要求,本篇介绍QMenu菜单的风格设计,包括样式表和阴影。 1.QMenu样式表的设计 首先看一个默认的菜单 void QGraphicsDropShadowEffectDemo::slotShowDialog() {qDebug() <&l…...

temu防窒息警示语贴哪里
防窒息警示语标签的位置选择是确保消费者在购买和使用产品时能够注意到潜在窒息风险的重要一环。本文将为您介绍一些关于防窒息警示语标签贴在哪里的建议,以帮助您选择合适的位置。 先给大家推荐一款拼多多/temu运营工具——多多情报通 多多情报通是拼多多的生意参…...
Maven——坐标和依赖
Maven的一大功能是管理项目依赖。为了能自动化地解析任何一个Java构件,Maven就必须将它们唯一标识,这就依赖管理的底层基础——坐标。将详细分析Maven坐标的作用,解释其每一个元素;在此基础上,再介绍如何配置Maven&…...

Python中事务的常见用法
在Python中,可以使用数据库连接对象来执行事务操作。以下是一些常见的 Python 中事务的用法: 开始事务 要开始一个事务,你需要获取数据库连接对象,并调用其 begin() 或 start_transaction() 方法来开启一个事务。例如࿰…...

蛮力法最大值连续子序问题
概念: 在一个给定的整数数组中找到一个连续的子序列,使得子序列的元素之和最大 思路: 遍历所有可能的子序列,计算它们的和。 在每次计算过程中,记录当前最大的子序列和。 返回最大的子序列和作为结果。 代码: #include <iostream> #…...

多功能智能遥测终端机 5G/4G+北斗多信道 视频采集传输
计讯物联多功能智能遥测终端机,全网通5G/4G无线通信、弱信号地区北斗通信,多信道自动切换保障通信联通,丰富网络接口及行业应用接口,支持水利、环保、工业传感器、控制终端、智能终端接入,模拟量/数字量/信号量采集&am…...
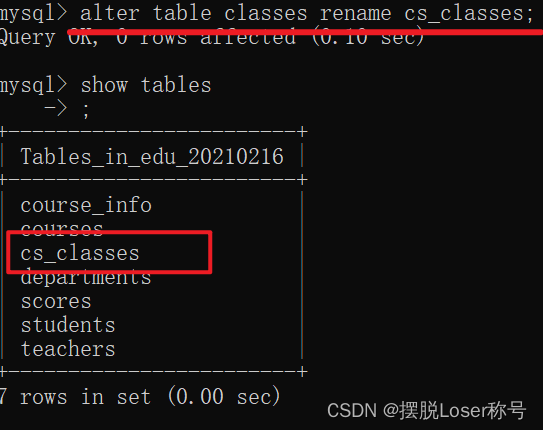
1.查看表的基本结构,表的详细结构和修改表名
查看表的基本结构,表的详细结构和修改表名 1.查看数据表基本结构 有强迫症或健忘症的小伙伴们在建好数据库和表以后,通常会怀疑自己刚才是不是敲错了,怎么办?如果不是使用图形界面是不是就没法查看啦? 不存在的,这就…...

Mybatis实用教程之XML实现动态sql
系列文章目录 1、mybatis简介及数据库连接池 2、mybatis中selectOne的使用 3、mybatis简单使用 4、mybatis中resultMap结果集的使用 Mybatis实用教程之XML实现动态sql 系列文章目录前言1. 动态条件查询2. 动态更新语句3. 动态插入语句4、其他标签的使用 前言 当编写 MyBatis 中…...
)
混合App开发实现页面跳转(更新中)
util.js /*** 这个函数被用来获取 URL 中的查询参数,并将它们以对象(键值对)的形式返回* param {string} url* returns {object} oParams*/ export function getUrlQuery(url null) {let sUrl url || window.location.href;let oParams {…...

【FPGA】Verilog:BCD 加法器的实现
0x00 XOR 运算在 2 的补码加减法中的应用 2 的补码加减法的特点是,当从某个数中减去负数时,将其转换为正数的加法来计算,并将减去正数的情况转换为负数的加法来计算,从而将所有减法运算转换为加法运算。在这种情况下,…...
机器学习第15天:GBDT模型
☁️主页 Nowl 🔥专栏《机器学习实战》 《机器学习》 📑君子坐而论道,少年起而行之 文章目录 GBDT模型介绍 Boosting 残差 GBDT的缺点 python代码实现 代码 模型参数解释 结语 GBDT模型介绍 GBDT(Gradient Boos…...

STM32F407-14.3.9-01输出比较模式
输出比较模式 此功能用于控制输出波形,或指示已经过某一时间段。 当捕获/比较寄存器与计数器之间相匹配时,输出比较功能: ● 将为相应的输出引脚分配一个可编程值,该值由输出比较模式(TIMx_CCMRx 寄存器中的 OCxM⑦…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
