【矩阵论】Chapter 4—特征值和特征向量知识点总结复习
文章目录
- 1 特征值和特征向量
- 2 对角化
- 3 Schur定理和正规矩阵
- 4 Python求解
1 特征值和特征向量
-
定义
设 σ \sigma σ为数域 F F F上线性空间 V V V上的一个线性变换,一个非零向量 v ∈ V v\in V v∈V,如果存在一个 λ ∈ F \lambda \in F λ∈F使得 σ ( v ) = λ v \sigma(v)=\lambda v σ(v)=λv,则 λ \lambda λ称为 σ \sigma σ的特征值。 σ \sigma σ的特征值的集合称为 σ \sigma σ的谱。并称 v v v为 σ \sigma σ的属于(或对应于)特征值 λ \lambda λ的特征向量。
-
特征值和特征向量的求法
设 V V V是数域 F F F上的 n n n维线性空间, v 1 , ⋯ , v n v_1,\cdots,v_n v1,⋯,vn是 V V V的一组基,线性变换 σ \sigma σ在这组基下的矩阵为 A A A,如果 λ \lambda λ是 σ \sigma σ的特征值, α \alpha α是相应的特征向量。则
α = ( v 1 , ⋯ , v n ) ( x 1 ⋮ x n ) \alpha=(v_1,\cdots,v_n)\begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix} α=(v1,⋯,vn) x1⋮xn
将上式代入 σ ( v ) = λ v \sigma(v)=\lambda v σ(v)=λv得到
σ ( α ) = ( v 1 , ⋯ , v n ) A ( x 1 ⋮ x n ) λ α = λ ( v 1 , ⋯ , v n ) ( x 1 ⋮ x n ) \sigma(\alpha)=(v_1,\cdots,v_n)A\begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix}\\ \lambda \alpha=\lambda (v_1,\cdots,v_n)\begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix}\\ σ(α)=(v1,⋯,vn)A x1⋮xn λα=λ(v1,⋯,vn) x1⋮xn
由于 v 1 , ⋯ , v n v_1,\cdots,v_n v1,⋯,vn线性无关,所以
A ( x 1 ⋮ x n ) = λ ( x 1 ⋮ x n ) A\begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix}=\lambda \begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix} A x1⋮xn =λ x1⋮xn
则说明特征向量 α \alpha α的坐标 x = ( x 1 ⋮ x n ) x=\begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix} x= x1⋮xn 满足齐次线性方程组 ( λ I − A ) x = 0 (\lambda I-A)x=0 (λI−A)x=0。因为 α ≠ 0 \alpha\neq 0 α=0,则 x ≠ 0 x\neq 0 x=0,即齐次线性方程组 ( λ I − A ) x = 0 (\lambda I-A)x=0 (λI−A)x=0有非零解。有非零解的充要条件是它的系数矩阵它的系数矩阵行列式 ∣ λ I − A ∣ = 0 |\lambda I-A|=0 ∣λI−A∣=0。
-
相关定义
设 A A A是数域 F F F上的 n n n阶矩阵, λ \lambda λ是一个符号,也是未知的特征值,矩阵 λ I − A \lambda I-A λI−A称为 A A A的特征矩阵,其行列式 ∣ λ I − A ∣ |\lambda I-A| ∣λI−A∣称为 A A A的特征多项式。方程 ∣ λ I − A ∣ = 0 |\lambda I-A|=0 ∣λI−A∣=0称为 A A A的特征方程,它的根(即 λ \lambda λ的值)称为 A A A的特征根(或特征值)。以 A A A的特征值 λ \lambda λ代入 A x = λ x Ax=\lambda x Ax=λx中所得到的非零解 x x x称为 A A A对应于 λ \lambda λ的特征向量。
-
定理
设 A A A为 n × n n\times n n×n矩阵, λ \lambda λ是一个数值,以下命题等价:
- λ \lambda λ是 A A A的特征值
- ( λ I − A ) x = 0 (\lambda I-A)x=0 (λI−A)x=0有一个非平凡的解(即有非零向量的解)
- N ( λ I − A ) ≠ { 0 } N(\lambda I-A)\neq\{0\} N(λI−A)={0}
- λ I − A \lambda I-A λI−A矩阵是奇异矩阵
- det ( λ I − A ) = 0 \det(\lambda I-A)=0 det(λI−A)=0
-
特征多项式的系数
如果
p ( λ ) = det ( λ I − A ) = λ n + ∑ k = 1 n ( − 1 ) k c k λ n − k = λ n − c 1 λ n − 1 + ⋯ + ( − 1 ) n − 1 c n − 1 λ + ( − 1 ) n c n p(\lambda)=\det(\lambda I-A)=\lambda^n+\sum_{\\k=1}^n(-1)^kc_k\lambda^{n-k}\\=\lambda ^n-c_1\lambda^{n-1}+\cdots+(-1)^{n-1}c_{n-1}\lambda+(-1)^nc_n p(λ)=det(λI−A)=λn+k=1∑n(−1)kckλn−k=λn−c1λn−1+⋯+(−1)n−1cn−1λ+(−1)ncn
则 c k ( 1 ≤ k ≤ n ) c_k(1\leq k\leq n) ck(1≤k≤n)是所有 k k k阶主子式(选择 k k k行 k k k列形成的行列式)的和,特别的, c 1 = t r ( A ) , c n = det ( A ) c_1=tr(A),c_n=\det(A) c1=tr(A),cn=det(A)。 -
定理
-
设 A ∈ C n × n A\in C^{n\times n} A∈Cn×n,如果 A A A有特征值 λ 1 , ⋯ , λ n \lambda_1,\cdots,\lambda_n λ1,⋯,λn,则
t r ( A ) = ∑ i = 1 n λ i , det ( A ) = ∏ i = 1 n λ i tr(A)=\sum_{\\i=1}^n\lambda_i,\det(A)=\prod_{i=1}^n\lambda_i tr(A)=i=1∑nλi,det(A)=i=1∏nλi -
如果 A A A相似 B B B,则两个矩阵有相同的特征值和特征多项式。
-
设 A ∈ C m × n A\in C^{m\times n} A∈Cm×n,则 A H A A^HA AHA和 A A H AA^H AAH特征值都是非负实数,且它们都有相同的非零特征值和相同的重数,并且非零特征值(包含重数)的数量等于 r a n k ( A ) rank(A) rank(A)。
-
2 对角化
-
定义
设矩阵 A ∈ F n × n A\in F^{n\times n} A∈Fn×n,如果存在一个非奇异矩阵 P ∈ F n × n P\in F^{n\times n} P∈Fn×n和一个对角矩阵 D ∈ F n × n D\in F^{n\times n} D∈Fn×n,使得 P − 1 A P = D P^{-1}AP=D P−1AP=D,则称 A A A可被对角化。
-
定理
- A A A可以被对角化当且仅当 A A A有 n n n个线性无关的特征向量
- λ 1 , ⋯ , λ k \lambda_1,\cdots,\lambda_k λ1,⋯,λk是 A A A的不同的特征值,则对应的特征向量 x 1 , ⋯ , x k x_1,\cdots,x_k x1,⋯,xk它们是线性无关的
- 由以上两条定理即可推出如果 A A A有 n n n个不同的特征值,则 A A A可被对角化
- 不同特征值对应的特征向量的集合的并集是线性无关的。即取每个特征值的所有特征向量,无论这些向量属于哪个特征值,它们的并集都是线性无关的。
-
代数重数
设 A ∈ F n × n A\in F^{n\times n} A∈Fn×n,如果 det ( λ I − A ) = ( λ − λ i ) r 1 ⋯ ( λ − λ k ) r k \det(\lambda I-A)=(\lambda -\lambda_i)^{r_1}\cdots(\lambda-\lambda_k)^{r_k} det(λI−A)=(λ−λi)r1⋯(λ−λk)rk,其中 λ 1 , ⋯ , λ k \lambda_1,\cdots,\lambda_k λ1,⋯,λk是 A A A的特征值,它们是不同的。则特征值 λ i \lambda_i λi的代数重数是 r i r_i ri,即特征值 λ i \lambda_i λi出现的次数。
-
几何重数
与特征值 λ i \lambda_i λi对应的特征子空间是 N ( λ i I − A ) N(\lambda_i I-A) N(λiI−A),则特征值 λ i \lambda_i λi的几何重数为 dim ( N ( λ i I − A ) ) \dim(N(\lambda_i I-A)) dim(N(λiI−A))。
几何重数$\leq $代数重数
-
几何重数看可对角化
矩阵 A ∈ F n × n A\in F^{n\times n} A∈Fn×n可对角化当且仅当 A A A中不同特征值的几何重数和等于 n n n(即每个特征值的代数重数都要等于几何重数)
3 Schur定理和正规矩阵
-
酉(正交)相似定义
设 A ∈ C n × n ( R n × n ) A\in C^{n\times n}(R^{n\times n}) A∈Cn×n(Rn×n),如果存在一个酉(正交)矩阵 U U U使得 U H A U = B ( U H = U − 1 ) U^HAU=B\space\space\space(U^H=U^{-1}) UHAU=B (UH=U−1),则可称 A A A酉(正交)相似 B B B
-
Schur定理
∀ A ∈ C n × n \forall A\in C^{n\times n} ∀A∈Cn×n, A A A都与上三角矩阵相似,且存在酉矩阵 U U U和上三角矩阵 T T T使得 U H A U = U − 1 A U = T U^HAU=U^{-1}AU=T UHAU=U−1AU=T。
仅适用于复数域,实数域上不一定适用
-
正规矩阵定义
设 A ∈ C n × n A\in C^{n\times n} A∈Cn×n,如果 A A A满足 A H A = A A H A^HA=AA^H AHA=AAH,则称 A A A是正规矩阵。
Hermite矩阵,酉(正交)矩阵都是正规矩阵
-
谱定理
设 A ∈ C n × n A\in C^{n\times n} A∈Cn×n,如果 A A A是Hermite矩阵,则 A A A酉相似于一个实对角矩阵,换句话说,Hermite矩阵的特征值都是实数。
-
引理
设 A ∈ C n × n A\in C^{n\times n} A∈Cn×n, A A A是正规矩阵当且仅当 ∀ λ , x \forall \lambda,x ∀λ,x使得 ∣ ∣ A x − λ x ∣ ∣ = ∣ ∣ A H x − λ ˉ x ∣ ∣ ||Ax-\lambda x||=||A^Hx-\bar{\lambda}x|| ∣∣Ax−λx∣∣=∣∣AHx−λˉx∣∣。
-
同时对角化
设 A , B A,B A,B都是相同阶数的正规矩阵,则存在一个酉矩阵可以同时酉对角化 A , B A,B A,B当且仅当 A B = B A AB=BA AB=BA
4 Python求解
import numpy as np
from sympy import symbols, Matrix
import pprint# 定义符号变量
lambda_ = symbols('lambda')A = np.array([[0, 2, 1], [-2, 0, 3], [-1, -3, 0]])
A = Matrix(A)# 求特征矩阵
characteristic_matrix = A - lambda_ * np.eye(3)
pprint.pprint("关于 lambda 的特征矩阵:")
pprint.pprint(characteristic_matrix)# 计算特征多项式
characteristic_polynomial = A.charpoly(lambda_)
pprint.pprint("关于 lambda 的特征多项式:")
pprint.pprint(characteristic_polynomial)# 求特征值
eigenvalues = A.eigenvals()
# 打印特征值、其代数重数、特征向量和几何重数for k, v in eigenvalues.items():pprint.pprint("特征值 %s 的代数重数为 %s" % (k, v))pprint.pprint("特征值 %s 的几何重数为 %s" % (k, A.eigenvects()[list(eigenvalues.keys()).index(k)][1]))pprint.pprint("特征值 %s 的特征向量为 %s" % (k, A.eigenvects()[list(eigenvalues.keys()).index(k)][2]))# 判断A是否可对角化,如果可以,打印出对角化矩阵
if A.is_diagonalizable():pprint.pprint("A可对角化")pprint.pprint("对角化矩阵为:")pprint.pprint(A.diagonalize()[0])# 求A的行空间、列空间、零空间
pprint.pprint("A的行空间为:")
pprint.pprint(A.rowspace())
pprint.pprint("A的列空间为:")
pprint.pprint(A.columnspace())
pprint.pprint("A的零空间为:")
pprint.pprint(A.nullspace())
相关文章:

【矩阵论】Chapter 4—特征值和特征向量知识点总结复习
文章目录 1 特征值和特征向量2 对角化3 Schur定理和正规矩阵4 Python求解 1 特征值和特征向量 定义 设 σ \sigma σ为数域 F F F上线性空间 V V V上的一个线性变换,一个非零向量 v ∈ V v\in V v∈V,如果存在一个 λ ∈ F \lambda \in F λ∈F使得 σ (…...

Linux 进程地址空间
知识回顾 在 C 语言的学习过程中,我们知道内存是可以被划分为栈区,堆区,全局数据区,字符常量区,代码区的。他的空间排布可能是下面的样子: 其中,全局数据区,可以划分为已初始化全局…...

websocket vue操作
let websocket: WebSocket; /** websocket测试 */ function connectWebsocket() {if (typeof WebSocket "undefined") {console.log("您的浏览器不支持WebSocket");return;}// let ip window.location.hostname ":8080";let ip "10.192…...
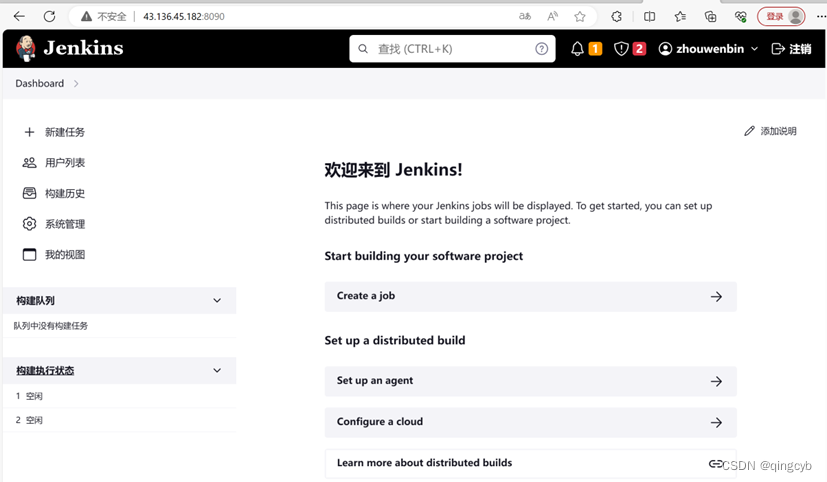
腾讯云CentOS8 jenkins war安装jenkins步骤文档
腾讯云CentOS8 jenkins war安装jenkins步骤文档 一、安装jdk 1.1 上传jdk-11.0.20_linux-x64_bin.tar.gz 1.2 解压jdk安装包文件 tar -zxvf jdk*.tar.gz 1.3 在/usr/local 目录下创建java目录 cd /usr/local mkdir java 1.4 切到java目录,把jdk解压文件改名为jd…...

Linux: glibc: net/if.h vs linux/if.h
最近看到一段代码改动,用net/if.h替换了linux/if.h。仔细看了看这两个的区别: https://stackoverflow.com/questions/20082433/what-is-the-difference-between-linux-if-h-and-net-if-h 从网上搜了一下看到如下的一个编译错误,如果同时使用这两个if.h文件,需要将net/if.h…...
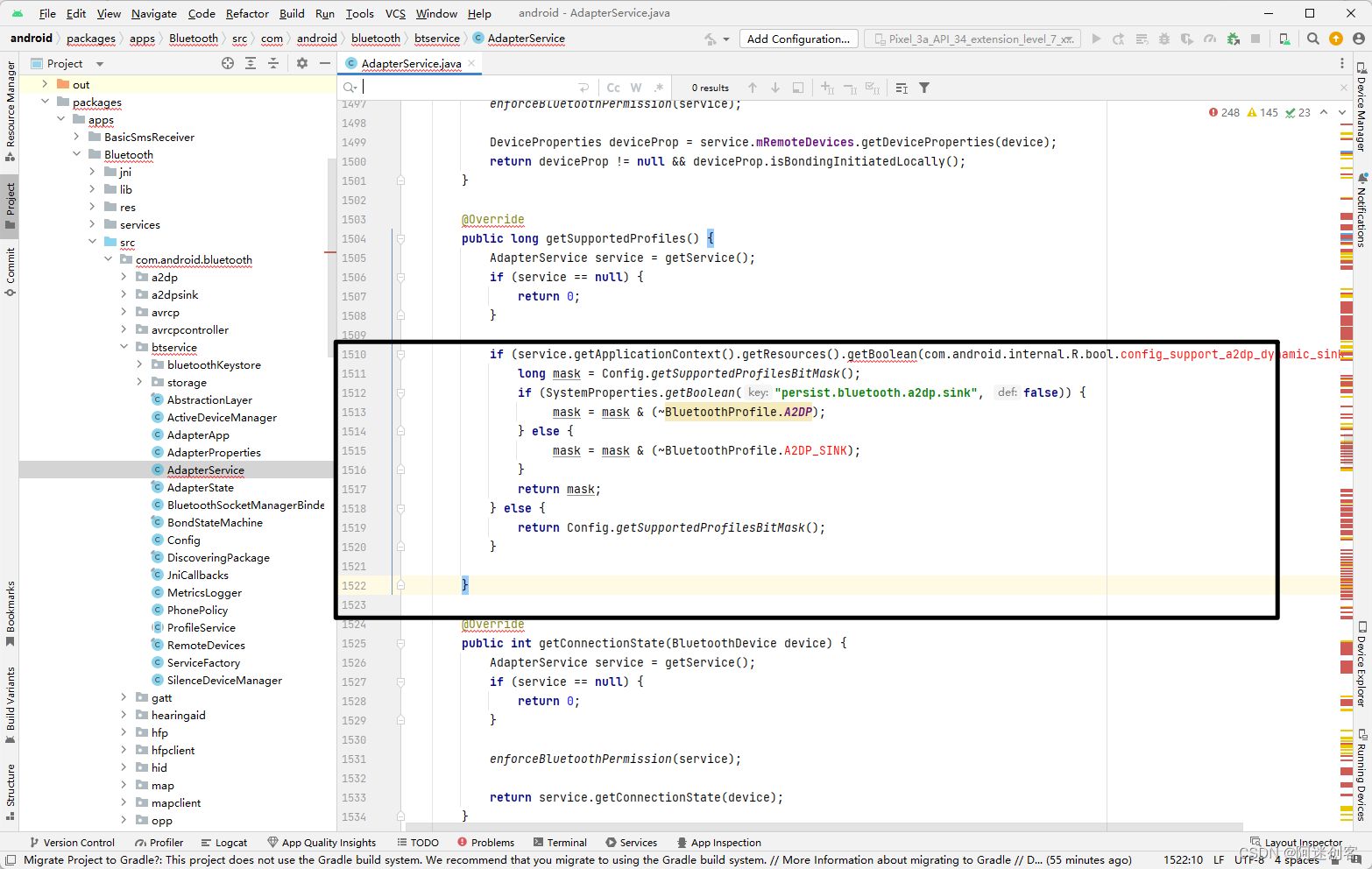
使用Android Studio导入Android源码:基于全志H713 AOSP,方便解决编译、编码问题
文章目录 一、 篇头二、 操作步骤2.1 编译AOSP AS工程文件2.2 将AOSP导入Android Studio2.3 切到Project试图2.4 等待index结束2.5 下载缺失的JDK 1.82.6 导入完成 三、 导入AS的好处3.1 本文案例演示源码编译错误AS对比同文件其余地方的调用AS错误提示依赖AS做错误修正 一、 篇…...

python random详解
文章目录 random简单示例1. 生成随机浮点数:2. 生成指定范围内的随机整数:3. 从序列中随机选择元素:4. 打乱序列顺序: 常用的方法及其解释和例子:1. random():该方法返回一个0到1之间的随机浮点数。例如&am…...
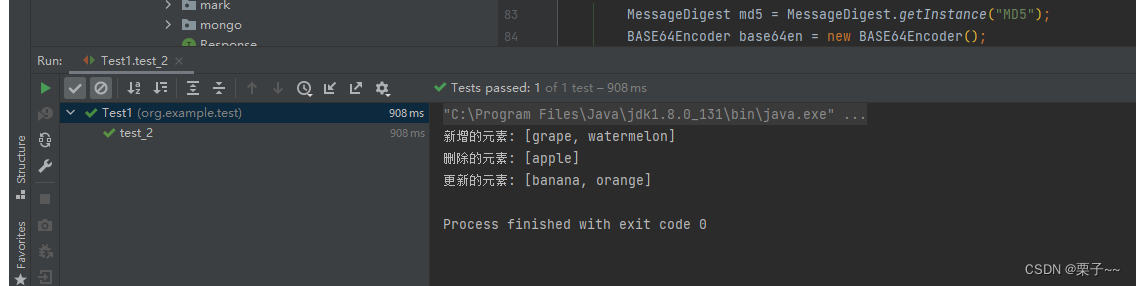
java-两个列表进行比较,判断那些是需要新增的、删除的、和更新的
文章目录 前言两个列表进行比较,判断那些是需要新增的、删除的、和更新的 前言 如果您觉得有用的话,记得给博主点个赞,评论,收藏一键三连啊,写作不易啊^ _ ^。 而且听说点赞的人每天的运气都不会太差,实…...
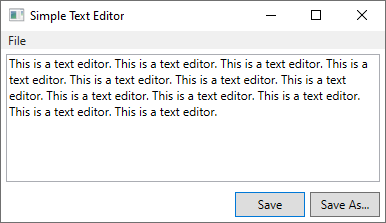
【WPF.NET开发】WPF中的对话框
目录 1、消息框 2、通用对话框 3、自定义对话框 实现对话框 4、打开对话框的 UI 元素 4.1 菜单项 4.2 按钮 5、返回结果 5.1 模式对话框 5.2 处理响应 5.3 非模式对话框 Windows Presentation Foundation (WPF) 为你提供了自行设计对话框的方法。 对话框是窗口&…...

NLP项目实战01之电影评论分类
介绍: 欢迎来到本篇文章!在这里,我们将探讨一个常见而重要的自然语言处理任务——文本分类。具体而言,我们将关注情感分析任务,即通过分析电影评论的情感来判断评论是正面的、负面的。 展示: 训练展示如下…...

一款可无限扩展的软件定时器开源框架项目代码
摘自链接 时间片轮询架构如何稳定高效实现,取代传统的标志位判断方式,更优雅更方便地管理程序的时间触发操作。 可以在STM32单片机上运行。...

GRE与顺丰圆通快递盒子
1. DNS污染 随想: 在输入一串网址后,会发生如下变化如果你在系统中配置了 Hosts 文件,那么电脑会先查询 Hosts 文件如果 Hosts 里面没有这个别名,就通过域名服务器查询域名服务器回应了,那么你的电脑就可以根据域名服…...
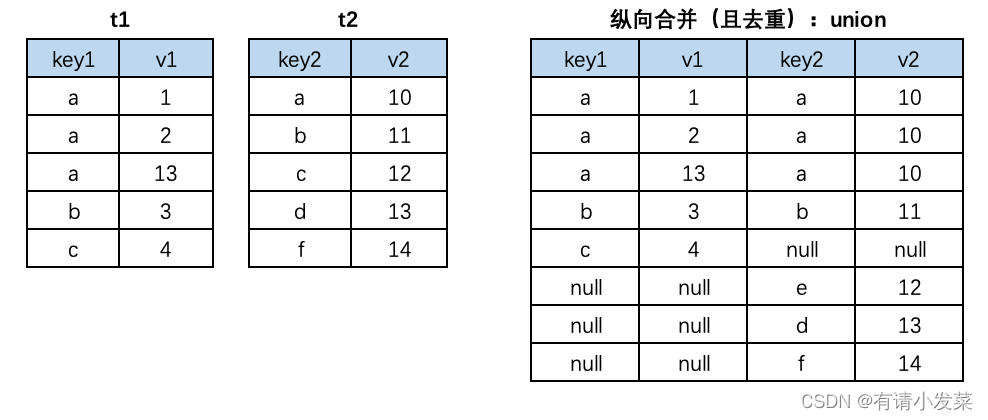
12.Mysql 多表数据横向合并和纵向合并
Mysql 函数参考和扩展:Mysql 常用函数和基础查询、 Mysql 官网 Mysql 语法执行顺序如下,一定要清楚!!!运算符相关,可前往 Mysql 基础语法和执行顺序扩展。 (8) select (9) distinct (11)<columns_name…...

线性回归与逻辑回归:深入解析机器学习的基石模型
目录 一、线性回归 二、逻辑回归 逻辑回归算法和 KNN 算法的区别 分类算法评价维度...

电脑待机怎么设置?让你的电脑更加节能
在日常使用电脑的过程中,合理设置待机模式是一项省电且环保的好习惯。然而,许多用户对于如何设置电脑待机感到困扰。那么电脑待机怎么设置呢?本文将深入探讨三种常用的电脑待机设置方法,通过详细的步骤,帮助用户更好地…...
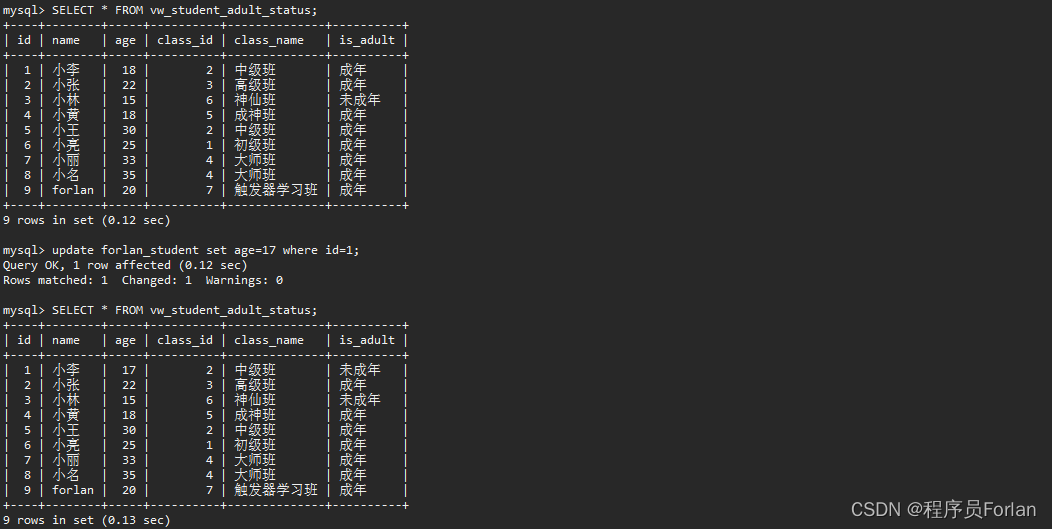
数据库对象介绍与实践:视图、函数、存储过程、触发器和物化视图
文章目录 一、视图(View)1、概念2、基本操作1)创建视图2)修改视图3)删除视图4)使用视图 3、使用场景4、实践 二、函数(Function)1、概念2、基本操作1)创建函数2ÿ…...

arm平台编译so文件回顾
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、几个点二、回顾过程 1.上来就执行Makefile2.编译第三方开源库.a文件 2.1 build.sh脚本2.2 Makefile3.最终编译三、其它知识点总结 前言 提示:这…...
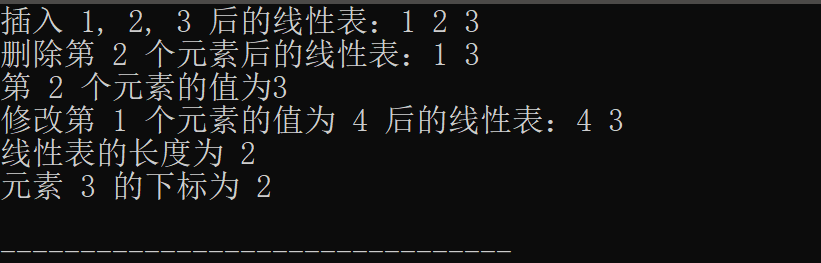
【数据结构】顺序表的定义和运算
目录 1.初始化 2.插入 3.删除 4.查找 5.修改 6.长度 7.遍历 8.完整代码 🌈嗨!我是Filotimo__🌈。很高兴与大家相识,希望我的博客能对你有所帮助。 💡本文由Filotimo__✍️原创,首发于CSDN📚。 &…...
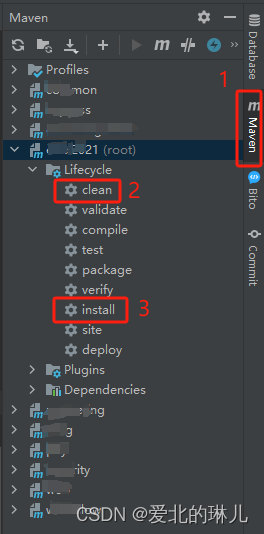
idea使用maven的package打包时提示“找不到符号”或“找不到包”
介绍:由于我们的项目是多模块开发项目,在打包时有些模块内容更新导致其他模块在引用该模块时不能正确引入。 情况一:找不到符号 情况一:找不到包 错误代码部分展示: Failure to find com.xxx.xxxx:xxx:pom:0.5 in …...

MetricBeat监控MySQL
目录 一、安装部署 二、开启mysql监控模块 三、编辑mysql配置文件 四、启动Metricbeat 五、查看监控图表 一、安装部署 metriceat的安装部署参考章节: Metricbeat安装使用,这里不再赘述。 二、开启mysql监控模块 进入metricbeat安装目录 ./metricb…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
