【C++学习手札】基于红黑树封装模拟实现map和set

🎬慕斯主页:修仙—别有洞天
💜本文前置知识: 红黑树
♈️今日夜电波:漂流—菅原纱由理
2:55━━━━━━️💟──────── 4:29
🔄 ◀️ ⏸ ▶️ ☰
💗关注👍点赞🙌收藏您的每一次鼓励都是对我莫大的支持😍
目录
一、前言
map和set的底层原理
二、红黑树的封装
通过模板使得map和set都可复用红黑树
迭代器类
operator++()
operator--()
红黑树类
仿函数
map
set
封装后的红黑树
begin()和end()
通过仿函数来控制要比较的值
完整封装
三、map和set的封装
封装后的set
封装后的map
四、完整代码
RBTree.h
myset.h
mymap.h
一、前言
本文主要叙述基于红黑树对于map和set的封装实现,需要有红黑树的知识前提。由于前面作者对于红黑树主要只是模拟实现了插入的功能。因此本文也只是实现map和set相应的功能,本文的主要要点在于map和set的封装以及迭代器中++和--的实现。
map和set的底层原理
C++中的map和set都是STL中的关联容器,都基于红黑树实现。其中set是K模型的容器,而map是KV模型的容器,本文主要讲述用一棵KV模型的红黑树同时实现map和set。map和set都使用红黑树的基本操作,时间复杂度为O(log n),其中n为元素数量。因此,map和set都是高效的关联容器。
二、红黑树的封装
通过模板使得map和set都可复用红黑树
可以看到我们定义了一个模板参数T,通过T的类型变化来改变红黑树中每一个节点的值,从而控制整颗红黑树的复用。
enum Colour
{RED,BLACK
};template<class T>
struct RBTreeNode
{RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;T _data;Colour _col;RBTreeNode(const T& data):_left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _col(RED){}
};迭代器类
迭代器实际上是对于指针进行操作,因此我们实例化并且重新命名了节点类的指针Node,由于迭代器分为是否常量迭代器,对此我们额外定义了两个模板参数Ref、Ptr用于控制其中重载运算符 T& operator*() 和 T* operator->()。当我们实例化时,区分Ref是const T&还是T&、Ptr是const T*还是T*。后面RBTree中会有所体现。在迭代器中,其中,operator*和operator->返回指向节点的指针,operator++和operator--实现前后缀++/--运算符,operator==和operator!=用来比较两个迭代器是否指向同一个节点。
以下为大致实现的功能:
template<class T, class Ref, class Ptr>
struct __TreeIterator
{typedef RBTreeNode<T> Node;typedef __TreeIterator<T, Ref, Ptr> Self;Node* _node;__TreeIterator(Node* node):_node(node){}Self& operator--();Self& operator++();Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}bool operator!=(const Self& s){return _node != s._node;}bool operator==(const Self& s){return _node == s._node;}};operator++()
对于map和set的遍历我们默认都是中序遍历,也就是左子树 根 右子树。因此对于++操作我们首要的是找到下一个节点,则这个下一个节点便是在这个节点的右子树,也就是而下一个节点的准确位置为:这个节点的右子树的最左节点(为什么呢?因为左 根 右我们将这个节点看作为根,则下一个节点位置为右子树,而右子树的第一个节点则为最左的节点)。 当这个节点的右为空,意味着包括这个节点在内的左 根 右都遍历完了,那么我们就需要向上遍历。则需遵循以下:如果孩子是父亲的左就返回父亲(这就是意味着遍历完了左 接下来要遍历 根),否则就继续向上遍历,如果走到nullptr那就是遍历完成。
总结一下遍历规则:
1、如果_node的右不为空,找右孩子的最左节点
2、如果_node的右为空,如果孩子是父亲的左就返回父亲,否则就继续向上遍历,如果走到nullptr那就是遍历完成
Self& operator++(){if (_node->_right){// 下一个就是右子树的最左节点Node* cur = _node->_right;while (cur->_left){cur = cur->_left;}_node = cur;}else{// 左子树 根 右子树// 右为空,找孩子是父亲左的那个祖先Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_right){cur = parent;parent = parent->_parent;}_node = parent;}return *this;} operator--()
和上面的operator++()相似,但是我们的遍历顺序变为了右子树 根 左子树。
总结一下遍历规则:
1、如果_node的左不为空,找左孩子的最右节点
2、如果_node的左为空,如果孩子是父亲的右就返回父亲,否则就继续向上遍历,如果走到nullptr那就是遍历完成
Self& operator--(){if (_node->_left){Node* cur = _node->_left;while (cur->_right){cur = cur->_right;}_node = cur;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_left){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}红黑树类
从之前我们所学习的红黑树的模拟实现我们可以知道,红黑树的插入等等操作中会用到对于key的比较。对此,set和map的比较要求是不同的,set可以直接用key进行比较,而map中对于pair的比较是先按first比较再比价second,而我们想要的结果是只比较first,因此我们定义了个KeyofT来对map和set进行区分。这个KeyofT则是通过传递仿函数来进行控制对于要比较值的转换。
// set->RBTree<K, K, SetKeyOfT> _t;
// map->RBTree<K, pair<const K, T>, MapKeyOfT> _t;
template<class K, class T, class KeyOfT>
class RBTree
{typedef RBTreeNode<T> Node;
public:typedef __TreeIterator<T, T&, T*> iterator;typedef __TreeIterator<T, const T&, const T*> const_iterator;iterator begin();iterator end();const_iterator begin();const_iterator end();//pair<iterator, bool> Insert(const T& data)pair<Node*, bool> Insert(const T& data);Node * Find(const K & key)private:Node* _root = nullptr;
};仿函数
注意:这里的仿函数是在map和set中定义的,我们在map和set中的迭代器实际上是就是间接的控制了RBTree的迭代器。
map
struct MapKeyOfT{const K& operator()(const pair<K, V>& kv){return kv.first;}};set
struct SetKeyOfT{const K& operator()(const K& key){return key;}};封装后的红黑树
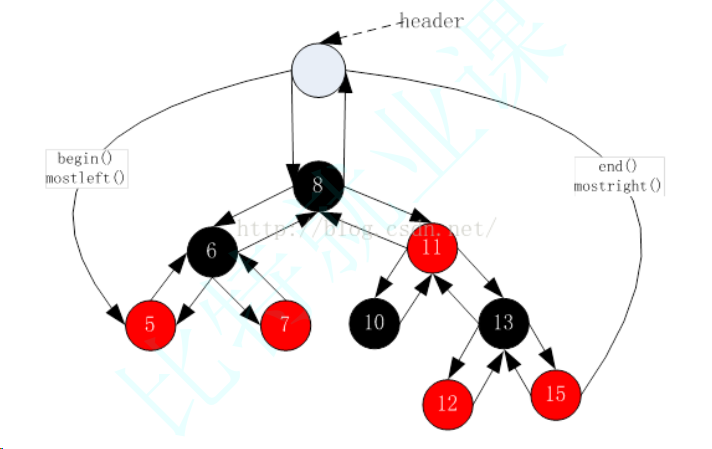
begin()和end()
STL明确规定,begin()与end()代表的是一段前闭后开的区间,而对红黑树进行中序遍历后,可以得到一个有序的序列,因此:begin()可以放在红黑树中最小节点(即最左侧节点)的位置,end()放在最大节点(最右侧节点)的下一个位置,关键是最大节点的下一个位置在哪块?能否给成nullptr呢?答案是行不通的,因为对end()位置的迭代器进行--操作,必须要能找最后一个元素,此处就不行,因此最好的方式是将end()放在头结点的位置:
虽然但是,作者还是将end()给了nullptr,事实上勉强还是可以用的哈哈哈...
iterator begin(){Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return iterator(cur);}iterator end(){return iterator(nullptr);}const_iterator begin() const{Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return const_iterator(cur);}const_iterator end() const{return const_iterator(nullptr);}通过仿函数来控制要比较的值
注意:这里对于insert以及find中都定义了一个KeyOfT kot; 这个就是上面所提到的用于转化用于比较的数据的仿函数的定义。
其中对于insert有点需要注意:我们运用了pair中的特性,用pair<Node*, bool>接收了make_pair(newnode, true)的返回值,用pair构造了一个新的pair而不是拷贝构造了一个pair。后续会提到为什么(在set封装中)
//pair<iterator, bool> Insert(const T& data)pair<Node*, bool> Insert(const T& data){if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return make_pair(_root, true);}Node* parent = nullptr;Node* cur = _root;KeyOfT kot;while (cur){if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return make_pair(cur, false);}}// 新增节点给红色cur = new Node(data);Node* newnode = cur;cur->_col = RED;if (kot(parent->_data) < kot(data)){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){// g// p u// cNode* uncle = grandfather->_right;if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上更新处理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_left){// 单旋// g// p// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// 双旋// g// p// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else // parent == grandfather->_right{// g// u p // c//Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// u p // c//RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return make_pair(newnode, true);}Node * Find(const K & key){Node* cur = _root;KeyOfT kot;while (cur!= nullptr){ if (kot(cur->_data) < key){cur = cur->_left;}else if (kot(cur->_data) > key){cur = cur->_right;}else{return cur;}}return nullptr;}完整封装
// set->RBTree<K, K, SetKeyOfT> _t;
// map->RBTree<K, pair<const K, T>, MapKeyOfT> _t;
template<class K, class T, class KeyOfT>
class RBTree
{typedef RBTreeNode<T> Node;
public:typedef __TreeIterator<T, T&, T*> iterator;typedef __TreeIterator<T, const T&, const T*> const_iterator;iterator begin(){Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return iterator(cur);}iterator end(){return iterator(nullptr);}const_iterator begin() const{Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return const_iterator(cur);}const_iterator end() const{return const_iterator(nullptr);}//pair<iterator, bool> Insert(const T& data)pair<Node*, bool> Insert(const T& data){if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return make_pair(_root, true);}Node* parent = nullptr;Node* cur = _root;KeyOfT kot;while (cur){if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return make_pair(cur, false);}}// 新增节点给红色cur = new Node(data);Node* newnode = cur;cur->_col = RED;if (kot(parent->_data) < kot(data)){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){// g// p u// cNode* uncle = grandfather->_right;if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上更新处理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_left){// 单旋// g// p// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// 双旋// g// p// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else // parent == grandfather->_right{// g// u p // c//Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// u p // c//RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return make_pair(newnode, true);}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* parentParent = parent->_parent;parent->_parent = subR;if (subRL)subRL->_parent = parent;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subR;}else{parentParent->_right = subR;}subR->_parent = parentParent;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* parentParent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subL;}else{parentParent->_right = subL;}subL->_parent = parentParent;}}void InOrder(){_InOrder(_root);cout << endl;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}// 根节点->当前节点这条路径的黑色节点的数量bool Check(Node* root, int blacknum, const int refVal){if (root == nullptr){//cout << balcknum << endl;if (blacknum != refVal){cout << "存在黑色节点数量不相等的路径" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "有连续的红色节点" << endl;return false;}if (root->_col == BLACK){++blacknum;}return Check(root->_left, blacknum, refVal)&& Check(root->_right, blacknum, refVal);}bool IsBalance(){if (_root == nullptr)return true;if (_root->_col == RED)return false;//参考值int refVal = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++refVal;}cur = cur->_left;}int blacknum = 0;return Check(_root, blacknum, refVal);}int Height(){return _Height(_root);}int _Height(Node* root){if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}size_t Size(){return _Size(_root);}size_t _Size(Node* root){if (root == NULL)return 0;return _Size(root->_left)+ _Size(root->_right) + 1;}Node * Find(const K & key){Node* cur = _root;KeyOfT kot;while (cur!= nullptr){ if (kot(cur->_data) < key){cur = cur->_left;}else if (kot(cur->_data) > key){cur = cur->_right;}else{return cur;}}return nullptr;}private:Node* _root = nullptr;
};三、map和set的封装
封装后的set
#pragma once
#include"RBTree.h"namespace bit
{template<class K>class set{public:struct SetKeyOfT{const K& operator()(const K& key){return key;}};typedef typename RBTree<K, K, SetKeyOfT>::const_iterator iterator;typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;iterator begin() const{return _t.begin();}iterator end() const{return _t.end();}pair<iterator, bool> insert(const K& key){return _t.Insert(key);}private:RBTree<K, K, SetKeyOfT> _t;};
}注意这段代码:
typedef typename RBTree<K, K, SetKeyOfT>::const_iterator iterator; typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;其中typenam是告诉编译器这里是类型因为这里是对类模板取内嵌类型。通过set的定义我们知道set不允许被修改数值,因此我们将两个迭代器实际上都定义为const_iterator。但是这样定义其中insert又出问题了,因为其中的返回类型会出现不匹配的情况,即pair<iterator, bool> 和_t.Insert(key)不匹配。因为我们return返回的实际上是iterator,而实际上接受的类型为const_iterator。这时我们上面提到的用pair构造了一个新的pair而不是拷贝构造了一个pair就起到作用了,他使得返回的类型匹配!
当然我们也有其他的解决办法:定义一个迭代器的拷贝构造
STL库中的普通迭代器都可以转换为const迭代器,这是迭代器类的拷贝构造所支持的。
如下:
struct __TreeIterator
{typedef RedBlackTreeNode<T> Node;Node* _node;typedef __TreeIterator<T,Ref,Ptr> Self;typedef __TreeIterator<T, T&, T*> iterator;__TreeIterator(const iterator& it):_node(it._node){}__TreeIterator(Node* node):_node(node){}
}
封装后的map
想较于set,map的key值不可修改,但是value是可以修改的,对于他的迭代器定义按照正常的const和非const就好,但是他主要做文章的地方是在RBTree<K, pair<const K, V>, MapKeyOfT> _t;中,直接将K定义为const K了。
#pragma once
#include"RBTree.h"namespace bit
{template<class K, class V>class map{public:struct MapKeyOfT{const K& operator()(const pair<K, V>& kv){return kv.first;}};// 对类模板取内嵌类型,加typename告诉编译器这里是类型typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::const_iterator const_iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}const_iterator begin() const{return _t.begin();}const_iterator end()const{return _t.end();}V& operator[](const K& key){pair<iterator, bool> ret = insert(make_pair(key, V()));return ret.first->second;}pair<iterator, bool> insert(const pair<K, V>& kv){return _t.Insert(kv);}private:RBTree<K, pair<const K, V>, MapKeyOfT> _t;};
}四、完整代码
RBTree.h
#pragma once// set ->key
// map ->key/valueenum Colour
{RED,BLACK
};template<class T>
struct RBTreeNode
{RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;T _data;Colour _col;RBTreeNode(const T& data):_left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _col(RED){}
};template<class T, class Ref, class Ptr>
struct __TreeIterator
{typedef RBTreeNode<T> Node;typedef __TreeIterator<T, Ref, Ptr> Self;Node* _node;__TreeIterator(Node* node):_node(node){}Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}Self& operator--(){if (_node->_left){Node* cur = _node->_left;while (cur->_right){cur = cur->_right;}_node = cur;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_left){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}Self& operator++(){if (_node->_right){// 下一个就是右子树的最左节点Node* cur = _node->_right;while (cur->_left){cur = cur->_left;}_node = cur;}else{// 左子树 根 右子树// 右为空,找孩子是父亲左的那个祖先Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_right){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}bool operator!=(const Self& s){return _node != s._node;}bool operator==(const Self& s){return _node == s._node;}
};// set->RBTree<K, K, SetKeyOfT> _t;
// map->RBTree<K, pair<const K, T>, MapKeyOfT> _t;
template<class K, class T, class KeyOfT>
class RBTree
{typedef RBTreeNode<T> Node;
public:typedef __TreeIterator<T, T&, T*> iterator;typedef __TreeIterator<T, const T&, const T*> const_iterator;iterator begin(){Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return iterator(cur);}iterator end(){return iterator(nullptr);}const_iterator begin() const{Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return const_iterator(cur);}const_iterator end() const{return const_iterator(nullptr);}//pair<iterator, bool> Insert(const T& data)pair<Node*, bool> Insert(const T& data){if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return make_pair(_root, true);}Node* parent = nullptr;Node* cur = _root;KeyOfT kot;while (cur){if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return make_pair(cur, false);}}// 新增节点给红色cur = new Node(data);Node* newnode = cur;cur->_col = RED;if (kot(parent->_data) < kot(data)){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){// g// p u// cNode* uncle = grandfather->_right;if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上更新处理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_left){// 单旋// g// p// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// 双旋// g// p// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else // parent == grandfather->_right{// g// u p // c//Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续往上处理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// u p // c//RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return make_pair(newnode, true);}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;Node* parentParent = parent->_parent;parent->_parent = subR;if (subRL)subRL->_parent = parent;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subR;}else{parentParent->_right = subR;}subR->_parent = parentParent;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* parentParent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subL;}else{parentParent->_right = subL;}subL->_parent = parentParent;}}void InOrder(){_InOrder(_root);cout << endl;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}// 根节点->当前节点这条路径的黑色节点的数量bool Check(Node* root, int blacknum, const int refVal){if (root == nullptr){//cout << balcknum << endl;if (blacknum != refVal){cout << "存在黑色节点数量不相等的路径" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "有连续的红色节点" << endl;return false;}if (root->_col == BLACK){++blacknum;}return Check(root->_left, blacknum, refVal)&& Check(root->_right, blacknum, refVal);}bool IsBalance(){if (_root == nullptr)return true;if (_root->_col == RED)return false;//参考值int refVal = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++refVal;}cur = cur->_left;}int blacknum = 0;return Check(_root, blacknum, refVal);}int Height(){return _Height(_root);}int _Height(Node* root){if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}size_t Size(){return _Size(_root);}size_t _Size(Node* root){if (root == NULL)return 0;return _Size(root->_left)+ _Size(root->_right) + 1;}Node * Find(const K & key){Node* cur = _root;KeyOfT kot;while (cur!= nullptr){ if (kot(cur->_data) < key){cur = cur->_left;}else if (kot(cur->_data) > key){cur = cur->_right;}else{return cur;}}return nullptr;}private:Node* _root = nullptr;
};myset.h
pragma once
#include"RBTree.h"namespace bit
{template<class K>class set{public:struct SetKeyOfT{const K& operator()(const K& key){return key;}};typedef typename RBTree<K, K, SetKeyOfT>::const_iterator iterator;typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;iterator begin() const{return _t.begin();}iterator end() const{return _t.end();}pair<iterator, bool> insert(const K& key){return _t.Insert(key);}private:RBTree<K, K, SetKeyOfT> _t;};
}mymap.h
#pragma once
#include"RBTree.h"namespace bit
{template<class K, class V>class map{public:struct MapKeyOfT{const K& operator()(const pair<K, V>& kv){return kv.first;}};// 对类模板取内嵌类型,加typename告诉编译器这里是类型typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::const_iterator const_iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}const_iterator begin() const{return _t.begin();}const_iterator end()const{return _t.end();}V& operator[](const K& key){pair<iterator, bool> ret = insert(make_pair(key, V()));return ret.first->second;}pair<iterator, bool> insert(const pair<K, V>& kv){return _t.Insert(kv);}private:RBTree<K, pair<const K, V>, MapKeyOfT> _t;};
}感谢你耐心的看到这里ღ( ´・ᴗ・` )比心,如有哪里有错误请踢一脚作者o(╥﹏╥)o!

给个三连再走嘛~
相关文章:

【C++学习手札】基于红黑树封装模拟实现map和set
🎬慕斯主页:修仙—别有洞天 💜本文前置知识: 红黑树 ♈️今日夜电波:漂流—菅原纱由理 2:55━━━━━━️💟──────── 4:29 …...

linux查看当前路径的所有文件大小;linux查看当前文件夹属于什么文件系统
1:指令查看当前路径所有文件内存空间大小;这样可以方便查询每个文件大小情况,根据需要进行删除 df -h // 根目录 du -ah --max-depth1 // 一级目录 虚拟机 du -ah -d 1 // 一级目录 设备使用 du -ah --max-depth2 // 二…...
PPT插件-好用的插件-超级文本-大珩助手
常用字体 内置了大量的常用字体,方便快捷的一键更换字体,避免系统字体过多卡顿 文字整理 包含删空白行、清理编号、清理格式,便于处理从网络上复制的资料 文本打散与合并 包含文本打散、文本合并,文本打散可实现将一个文本打散…...

Kafka中的Topic
在Kafka中,Topic是消息的逻辑容器,用于组织和分类消息。本文将深入探讨Kafka Topic的各个方面,包括创建、配置、生产者和消费者,以及一些实际应用中的示例代码。 1. 介绍 在Kafka中,Topic是消息的逻辑通道࿰…...
LAMP部署
目录 一、安装apache 二、配置mysql 三、安装php 四、搭建论坛 4、安装另一个网站 一、安装apache 1.关闭防火墙,将安装Apache所需软件包传到/opt目录下 systemctl stop firewalld systemctl disable firewalld setenforce 0 httpd-2.4.29.tar.gz apr-1.6.2.t…...

DouyinAPI接口开发系列丨商品详情数据丨视频详情数据
电商API就是各大电商平台提供给开发者访问平台数据的接口。目前,主流电商平台如淘宝、天猫、京东、苏宁等都有自己的API。 二、电商API的应用价值 1.直接对接原始数据源,数据提取更加准确和完整。 2.查询速度更快,可以快速响应用户请求实现…...
AWS Remote Control ( Wi-Fi ) on i.MX RT1060 EVK - 3 “编译 NXP i.MX RT1060”( 完 )
此章节叙述如何修改、建构 i.MX RT1060 的 Sample Code“aws_remote_control_wifi_nxp” 1. 点击“Import SDK example(s)” 2. 选择“MIMXRT1062xxxxA”>“evkmimxrt1060”,并确认 SDK 版本后,点击“Next>” 3. 选择“aws_examples”>“aw…...

5G - NR物理层解决方案支持6G非地面网络中的高移动性
文章目录 非地面网络场景链路仿真参数实验仿真结果 非地面网络场景 链路仿真参数 实验仿真结果 Figure 5 && Figure 6:不同信噪比下的BER和吞吐量 变量 SISO 2x2MIMO 2x4MIMO 2x8MIMOReyleigh衰落、Rician衰落、多径TDL-A(NLOS) 、TDL-E(LOS)(a)QPSK (b)16…...

python epub文件解析
python epub文件解析 代码BeautifulSoup 介绍解释 代码 import ebooklib from bs4 import BeautifulSoup from ebooklib import epubbook epub.read_epub("逻辑思维训练1200题.epub")# 解析 for item in book.get_items():# 提取书中的文本内容if item.get_type() …...

Visual Studio 2015 中 FFmpeg 开发环境的搭建
Visual Studio 2015 中 FFmpeg 开发环境的搭建 Visual Studio 2015 中 FFmpeg 开发环境的搭建新建控制台工程拷贝并配置 FFmpeg 开发文件测试FFmpeg 开发文件的下载链接 Visual Studio 2015 中 FFmpeg 开发环境的搭建 新建控制台工程 新建 Win32 控制台应用程序。 具体流程&…...

期末速成数据库极简版【存储过程】(5)
目录 【7】系统存储过程 【8】用户存储过程——带输出参数的存储过程 创建存储过程 存储过程调用 【9】用户存储过程——不带输出参数的存储过程 【7】系统存储过程 系统存储我们就不做过程讲解用户存储过程会考察一道大题,所以我们把重点放在用户存储过程。…...

Android Studio的代码笔记--IntentService学习
IntentService学习 IntentService常规用法清单注册服务服务内容开启服务 IntentService 一个 HandlerThread工作线程,通过Handler实现把消息加入消息队列中等待执行,通过传递的intent在onHandleIntent中处理任务。(多次调用会按顺序执行事件…...

C语言 - 字符函数和字符串函数
系列文章目录 文章目录 系列文章目录前言1. 字符分类函数islower 是能够判断参数部分的 c 是否是⼩写字⺟的。 通过返回值来说明是否是⼩写字⺟,如果是⼩写字⺟就返回⾮0的整数,如果不是⼩写字⺟,则返回0。 2. 字符转换函数3. strlen的使⽤和…...
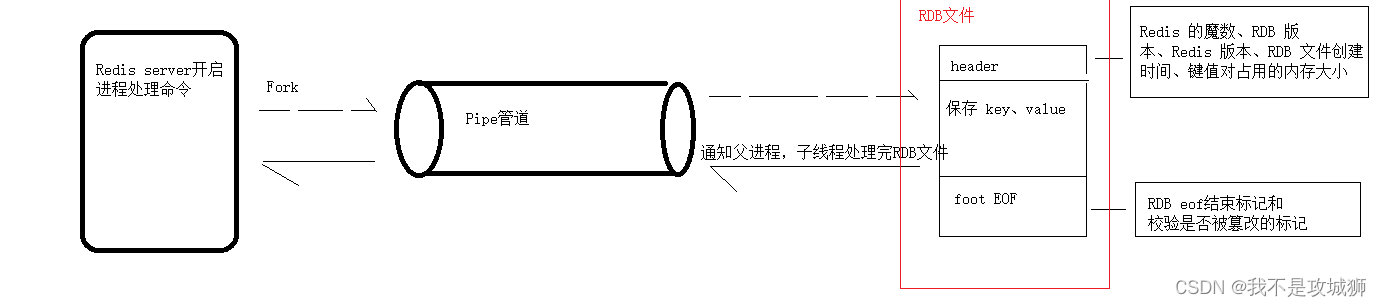
Redis rdb源码解析
前置学习:Redis server启动源码-CSDN博客 1、触发时机 1、执行save命令--->rdbSave函数 2、执行bgsave命令--->rdbSaveBackground函数或者(serverCron->prepareForShutdown) 3,主从复制-->startBgsaveForReplication…...

深入理解CyclicBarrier
文章目录 1. 概念2. CylicBarier使用简单案例3. 源码 1. 概念 CyclicBarrier 字面意思回环栅栏(循环屏障),通过它可以实现让一组线程等待至某个状态(屏障点)之后再全部同时执行。叫做回环是因为当所有等待线程都被释放…...

微信小程序 - 格式化操作 moment.js格式化常用使用方法总结大全
格式化操作使用 1. 首先,下载一个第三方库 moment npm i moment --save 注:在微信小程序中无法直接npm 下载 导入 的(安装一个就需要构建一次) 解决:菜单栏 --> 工具 --> 构建 npm 点击即可(会…...

学习pytorch18 pytorch完整的模型训练流程
pytorch完整的模型训练流程 1. 流程1. 整理训练数据 使用CIFAR10数据集2. 搭建网络结构3. 构建损失函数4. 使用优化器5. 训练模型6. 测试数据 计算模型预测正确率7. 保存模型 2. 代码1. model.py2. train.py 3. 结果tensorboard结果以下图片 颜色较浅的线是真实计算的值&#x…...

电子学会C/C++编程等级考试2021年09月(五级)真题解析
C/C++等级考试(1~8级)全部真题・点这里 第1题:抓牛 农夫知道一头牛的位置,想要抓住它。农夫和牛都位于数轴上,农夫起始位于点N(0<=N<=100000),牛位于点K(0<=K<=100000)。农夫有两种移动方式: 1、从X移动到X-1或X+1,每次移动花费一分钟 2、从X移动到2*X,每…...
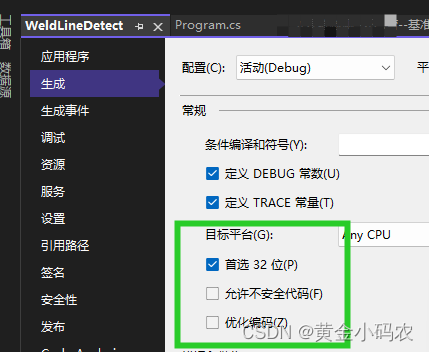
Halcon联合winform显示以及处理
在窗口中添加窗体和按钮,并在解决方案资源管理器中调加了导入Halcon导出的.cs文件,运行出现下图的问题: 问题1:CS0017 程序定义了多个入口点。使用/main(指定包含入口点的类型)进行编译。 解决方案1.: 右…...
【设计模式-4.3】行为型——责任链模式
说明:本文介绍设计模式中行为型设计模式中的,责任链模式; 审批流程 责任链模式属于行为型设计模式,关注于对象的行为。责任链模式非常典型的案例,就是审批流程的实现。如一个报销单的审批流程,根据报销单…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...