当前位置： 首页 > news >正文

深度学习 时间序列回归学习笔记

news 2026/2/11 8:56:00

目录

常用的深度学习时间序列回归模型：

ARIMA模型

ETS模型

效果评估

相关文章：

深度学习 时间序列回归学习笔记

目录 常用的深度学习时间序列回归模型： ARIMA模型 ETS模型 效果评估...

编程日记 2023/12/10 7:59:00

【postgresql】ERROR: INSERT has more expressions than target columns

执行下面sql insert into apply_account_cancellation3 select * from pply_account_cancellation; 返回下面错误信息 insert into apply_account_cancellation3 select * from apply_account_cancellation > ERROR: INSERT has more expressions than target colu…...

编程日记 2023/12/10 7:56:58

Android Kotlin语言下的文件存储

目录 将数据存储到文件中 创建文件和保存数据 读取文件 SharedPreferences存储 存储数据到SharedPreferences中 Context类中的getSharedPreferences()方法 Activity类中的getPreferences()方法 从SharedPreferences中读取数据 SQLite数据库存储 创建数据库 调用数据…...

编程日记 2023/12/10 7:55:57

Verilog 入门（八）（验证）

文章目录 编写测试验证程序波形产生值序列重复模式 测试验证程序实例从文本文件中读取向量实例：时序检测器 测试验证程序用于测试和验证设计方法的正确性。Verilog 提供强有力的结构来说明测试验证程序。 编写测试验证程序 测试验证程序有三个主要目的：…...

编程日记 2023/12/10 7:53:56

vue3 vue-router 导航守卫 （五）

在Vue 3中，导航守卫仍然是一个重要的概念，用于在路由切换时执行一些特定的逻辑。Vue Router提供了多个导航守卫，包括全局守卫、路由独享守卫和组件内守卫。可以在路由切换时执行一些特定的逻辑，例如身份验证、权限控制、数据加载等…...

编程日记 2023/12/10 7:51:53

Git命令---查看远程仓库

介绍 使用git命令查看绑定的远程仓库。 命令 git remote -v...

编程日记 2023/12/10 7:50:52

12.8作业

1. 使用手动连接，将登录框中的取消按钮使用qt4版本的连接到自定义的槽函数中，在自定义的槽函数中调用关闭函数 将登录按钮使用qt5版本的连接到自定义的槽函数中，在槽函数中判断ui界面上输入的账号是否为"admin"，密码是…...

编程日记 2023/12/10 7:49:51

算法：有效的括号（入栈出栈）

时间复杂度 O(n) 空间复杂度 O(n∣Σ∣)，其中 Σ 表示字符集，本题中字符串只包含 6 种括号 /*** param {string} s* return {boolean}*/ var isValid function(s) {const map {"(":")","{":"}","["…...

编程日记 2023/12/10 7:48:51

vxworks常用的指令归纳

目的：方便自己查阅 tftpboot 0x10000000 vxworks bootelf 0x10000000 ifconfig "gem0 dowm" ifconfig "gem0 inet 192.168.0.81" ifconfig "gem0 lladdr 01:02:03:04:05:06:07" ifconfig "gem0 up" ld 0,1,"…...

编程日记 2023/12/10 7:43:46

线性回归实战

3.1 使用正规方程进行求解 3.1.1 简单线性回归 公式 ： y w x b y wx b ywxb 一元一次方程，在机器学习中一元表示一个特征，b表示截距，y表示目标值。 使用代码进行实现： 导入包 import numpy as np import matp…...

编程日记 2023/12/10 7:42:46

stm32 使用18B20 测试温度

用18b20 测试温度是非常常用的，不过18B20的调试不是这么容易的，有些内容网上很多的，不再重复说了，我先把波形说一下，再说程序部分： 整个都温度数据的顺序是： 1.700uS的低电平复位并测试18B20的…...

编程日记 2023/12/10 7:39:43

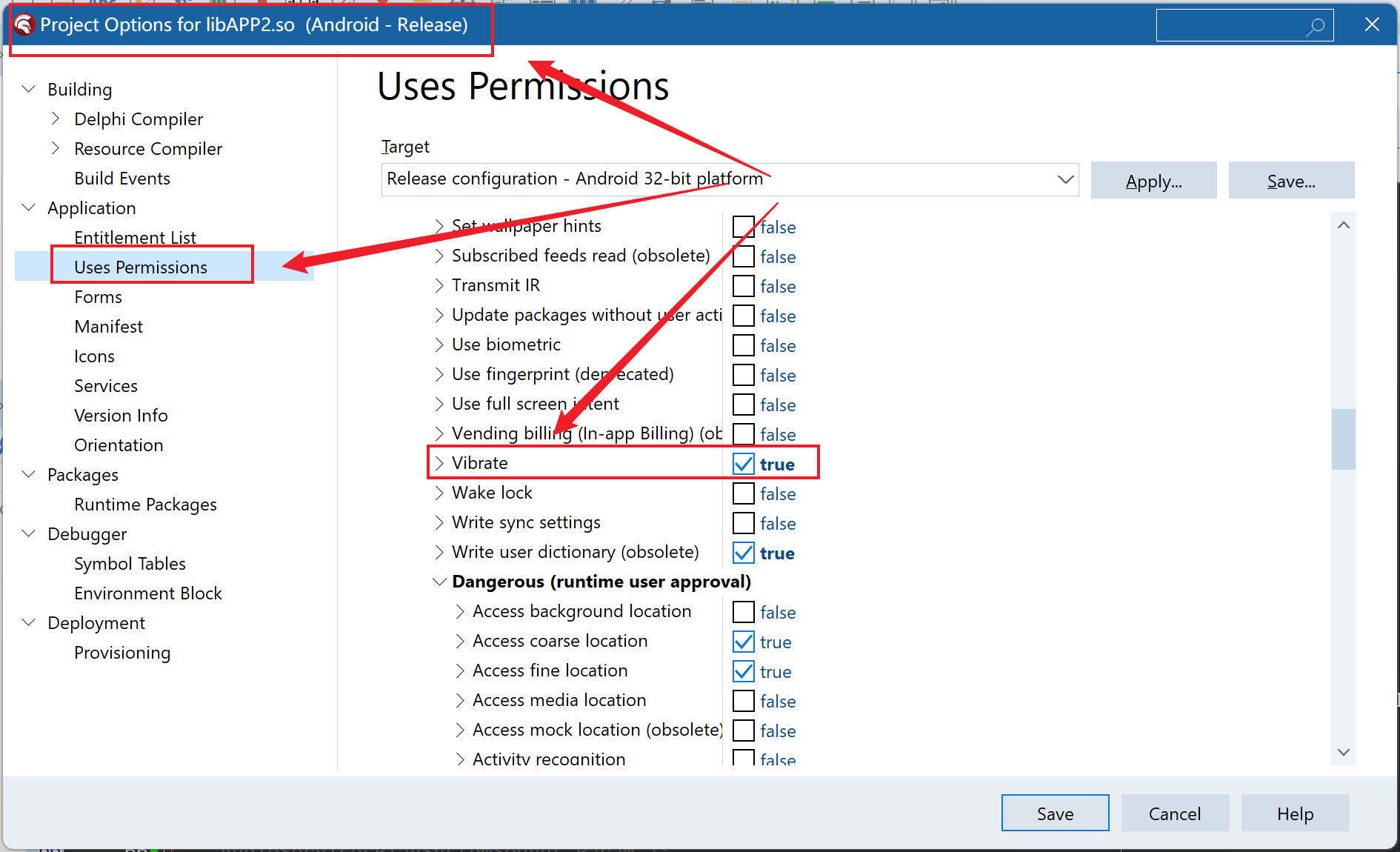
【Delphi】一个函数实现ios，android震动功能 Vibrate（包括3D Touch 中 Peek 震动等）

一、前言 我们在开发移动端APP的时候，有时可能需要APP能够提供震动功能，以便提醒操作者，特别是ios提供的3D Touch触感功能，操作者操作时会有触感震动，给操作者的感觉很友好。那么，在Delphi的移动端FMX开发中…...

编程日记 2023/12/10 7:38:42

国产Type-C PD芯片—接口快充取电芯片

常用USB PDTYPE-C受电端，即设备端协议IC芯片（PD Sink，也叫PD诱骗芯片），诱导取电芯片。 产品介绍 LDR6328: ◇ 采用 SOP-8 封装 ◇ 兼容 USB PD 3.0 规范，支持 USB PD 2.0 ◇ 兼容 QC 3.0 规范&#x…...

编程日记 2023/12/10 7:37:41

pytorch学习6-非线性变换（ReLU和sigmoid）

系列文章目录 pytorch学习1-数据加载以及Tensorboard可视化工具pytorch学习2-Transforms主要方法使用pytorch学习3-torchvisin和Dataloader的使用pytorch学习4-简易卷积实现pytorch学习5-最大池化层的使用pytorch学习6-非线性变换（ReLU和sigmoid）pytorc…...

编程日记 2023/12/10 7:35:40

详解Keras3.0 Models API: Whole model saving loading

1、save方法 Model.save(filepath, overwriteTrue, **kwargs) 将模型另存为.keras文件 参数说明 filepath: 保存模型的路径。必须以.keras结尾overwrite：布尔值，表示是否覆盖已存在的文件。默认为 True，即覆盖已存在的文件。save_format…...

编程日记 2023/12/10 7:32:37

Spring Cloud Gateway 网关的基础使用

1. 什么是网关？网关有什么用？ 在微服务架构中，网关就是一个提供统一访问地址的组件，它解决了内部微服务与外部的交互问题。网关主要负责流量的路由和转发，将外部请求引到对应的微服务实例上。同时提供身份认证、授权、…...

编程日记 2023/12/10 7:27:32

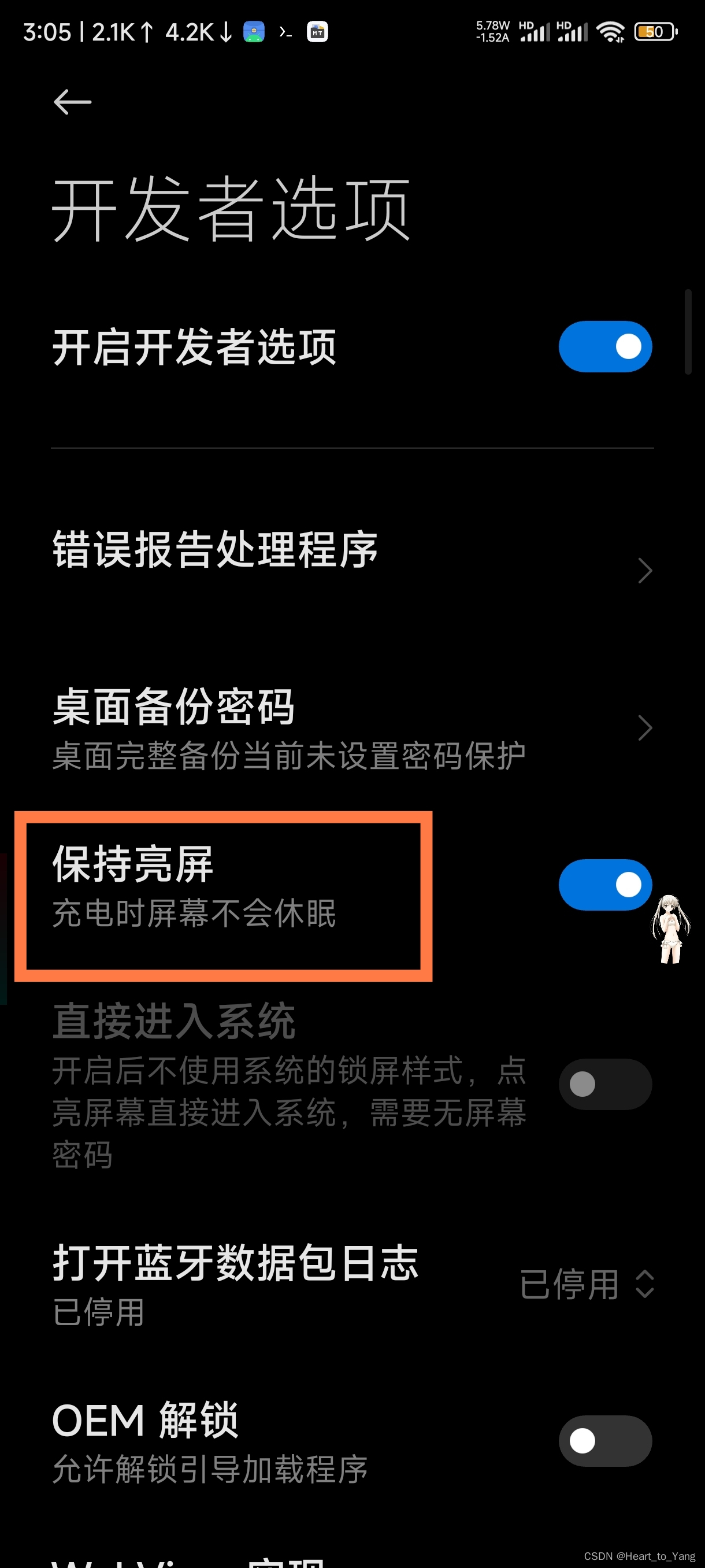
小米手机锁屏时间设置为永不休眠_手机不息屏_保持亮屏

环境：打开手机自带的锁屏时间设置发现没有 永不息屏的选项 原因：采用了三星OLED屏幕，所以根据OLED屏幕特性，这个是为了防止烧屏而特意设计的。非OLED机型支持设置“永不” 解决方案1：原生系统是支持永不锁屏的&#…...

编程日记 2023/12/10 7:26:31

lightdb plorasql集合类型新增可变数组

文章目录 背景集合类型可变数组可变数组示例 背景 在信创适配中，从Oracle迁移过来的存储过程使用到可变数组。因此在LightDB-X 23.4版本中对现有的集合类型进行了增强，添加了可变数组类型。 集合类型 在LightDB-X 23.4版本开始plorasql支持的集合类型…...

编程日记 2023/12/10 7:25:30

算法--最短路

这里写目录标题 xmind单源最短路简介所有边权都是正朴素的Dijkstra算法思想例子题解 堆优化版的Dijkstra算法 存在负数权Bellman-Ford算法思想例子题解 spfa算法思想例子题解 spfa判断负环思想例子题解 多源汇最短路简介弗洛伊德算法思想例子题解 小tips xmind 上述中&#xff…...

编程日记 2023/12/10 7:24:29

Linux 定时任务备份MySQL数据库

Linux 定时任务基本知识 crontab yum install crontabs （安装 crontabs） systemctl enable crond （设为开机启动） systemctl start crond（启动crond服务） systemctl status crond （查看状态&a…...

编程日记 2023/12/10 7:22:27

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造，完美适配AGV和无人叉车。同时，集成以太网与语音合成技术，为各类高级系统（如MES、调度系统、库位管理、立库等）提供高效便捷的语音交互体验。 L…...

编程新知 2026/2/10 23:40:34

idea大量爆红问题解决

问题描述 在学习和工作中，idea是程序员不可缺少的一个工具，但是突然在有些时候就会出现大量爆红的问题，发现无法跳转，无论是关机重启或者是替换root都无法解决 就是如上所展示的问题，但是程序依然可以启动。 问题解决…...

编程新知 2026/2/8 6:37:38

大数据零基础学习day1之环境准备和大数据初步理解

学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 （1）设置网关 打开VMware虚拟机，点击编辑…...

编程新知 2026/1/25 14:43:07

2025盘古石杯决赛【手机取证】

前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来，实在找不到，希望有大佬教一下我。 还有就会议时间，我感觉不是图片时间，因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

编程新知 2026/1/29 17:12:17

Android15默认授权浮窗权限

我们经常有那种需求，客户需要定制的apk集成在ROM中，并且默认授予其【显示在其他应用的上层】权限，也就是我们常说的浮窗权限，那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

编程新知 2026/2/1 4:13:59

智能仓储的未来：自动化、AI与数据分析如何重塑物流中心

当仓库学会“思考”，物流的终极形态正在诞生 想象这样的场景： 凌晨3点，某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径；AI视觉系统在0.1秒内扫描包裹信息；数字孪生平台正模拟次日峰值流量压力…...

编程新知 2026/2/1 2:49:30

代理篇12|深入理解 Vite中的Proxy接口代理配置

在前端开发中，常常会遇到 跨域请求接口 的情况。为了解决这个问题，Vite 和 Webpack 都提供了 proxy 代理功能，用于将本地开发请求转发到后端服务器。 什么是代理（proxy）？ 代理是在开发过程中，前端项目通过开发服务器，将指定的请求“转发”到真实的后端服务器，从而绕…...

编程新知 2025/10/27 20:33:34

算法：模拟

1.替换所有的问号 1576. 替换所有的问号 - 力扣（LeetCode） ​遍历字符串​：通过外层循环逐一检查每个字符。​遇到 ? 时处理​： 内层循环遍历小写字母（a 到 z）。对每个字母检查是否满足： ​与…...

编程新知 2026/2/10 11:15:52

【Go语言基础【12】】指针：声明、取地址、解引用

文章目录 零、概述：指针 vs. 引用（类比其他语言）一、指针基础概念二、指针声明与初始化三、指针操作符1. &：取地址（拿到内存地址）2. *：解引用（拿到值） 四、空指针&am…...

编程新知 2025/6/21 2:18:57

20个超级好用的 CSS 动画库

分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码，而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库，可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画，可以包含在你的网页或应用项目中。 3.An…...

编程新知 2026/2/9 22:04:45