数据结构之归并排序及排序总结
目录
归并排序
归并排序的时间复杂度
排序的稳定性
排序总结
归并排序
归并排序大家只需要掌握其递归方法即可,非递归方法由于在某些特殊场景下边界难控制,我们一般很少使用非递归实现归并排序。那么归并排序的递归方法我们究竟是怎样实现呢?
大家先想象一下这样一种场景,如果现在有两个数,我们要将这两个数排成升序,怎样呢?很简单,我们只需要将两个数进行一次大小的比较即可,比较完之后,小的元素放在前面,大的元素放在后面,其实这就是很简单的一次归并排序,两个素比较之后交换使得两个元素变得有序的场景我们就称作一次归并。
我们再次深入分析,如果有两个元素,这两个元素可以直接比较,且比较之后两个数就变得有序,以此类推,如果们要对4个元素进行归并排序,按照此逻辑,将两两分成一组,然后这两组进行一次比较,比较完成之后,这4个元素应该就变有序了,但是事实真是这样吗?通过示意图为大家讲解:

为什么两个元素互相比较就可以变得有序呢?
这是因为当一个数组中只有一个数时,我们就可以称这个数组是有序的,当数组中有两个元素时,我们可以将这两个数每一个数都看成一个数组,此时这两个数组都是有序的,两个有序的数组,元素之间依次比较,肯定会将最终的整个数组变得有序,所以,我们要使四个数组变得有序,可以将数组分成左右两个数组,当我们使左右两个数组有序时,再将左右两个数组的元素依次进行比较,这样,最终四个数组成的数组就会有序。以此,归并排序的递归思路就出来了:
通过四个元素的数组为大家图示讲解归并排序的思想:
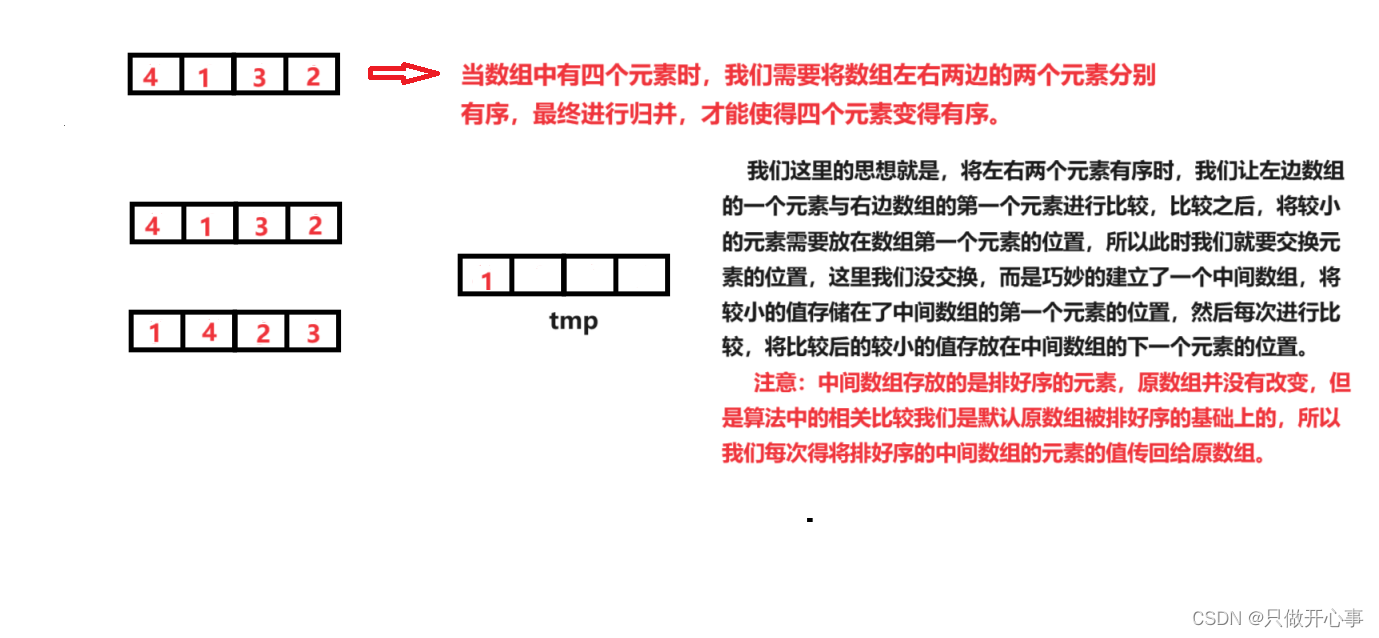
归并排序的思想:我们要对一个数组进行归并排序,使它变得有序,我们就得先将这个数组分成左右两部分,相对左边这部分数组进行归并排序,然后再对右边这部分数组进行归并排序,左右两边的数组排好序之后,对左右两个数组的元素进行一次比较,我们也成对左右两个数组的元素进行归并,然后整个数组的归并排序就完成了。
归并排序的整体代码:
void _MergeSort(int* a, int left, int right, int* tmp)
{if (left >= right)return;int mid = (right + left) / 2;_MergeSort(a, left, mid, tmp);_MergeSort(a, mid + 1, right, tmp);int begin1 = left, begin2 = mid + 1;int end1 = mid, end2 = right;int i = left;//左右数组有序之后,就需要左右数组进行归并while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}//左右两个数组,当一个数组归并完时,一个数组可能还没有归并完,将没有归并完的这个数组的元素依次赋值给中间数组while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin1 <= end1){tmp[i++] = a[begin2++];}for (int j = 0; j < right + 1; j++){a[j] = tmp[j];}
}
void MergeSort(int* a, int size)
{int* tmp = (int*)malloc(sizeof(int) * size);if (tmp == NULL){printf("malloc fail");exit(-1);}_MergeSort(a, 0, size - 1, tmp);free(tmp);tmp = NULL;
}
int main()
{int arr[] = {99,88,66,77,55,44,33,22,11 };MergeSort(arr,sizeof(arr)/sizeof(int));for (int i = 0; i < sizeof(arr) / sizeof(int); i++){printf("%d ", arr[i]);}return 0;
}运行截图:

归并排序的时间复杂度
时间复杂度:O(N*logN)
稳定性:稳定
排序的稳定性
什么是排序的稳定性呢?
其实就是,在未排序之前,数组中有两个相同的元素(有顺序),如果在排序之后这两个元素的顺序没有发生变化,则称这个排序是稳定的,如果排序之后顺序发生了变化,我们就称这个排序算法是不稳定的。
排序总结
直接插入排序:最好的情况下就是一个有序数组,插入的元素只用跟前面数组的最后一个元素比较,最好复杂度为O(N)。最坏的情况就是一个逆序数组,每个要插入的元素都要和前面的数组元素比较一下,就是等差数列求和O(N^2)
希尔排序:时间复杂度不好计算,大概是O(N^1.3)
选择排序:没有最好和最坏,编译器不知道所以,每个元素都和最小的元素比较一次,一趟排序确定了一元素的位置,剩下的元素下一趟继续进行比较,时间复杂度为等差数列求和O(N^2)
堆排序:没有最好和最坏,因为都是从一个大堆或者小堆进行调整,为O(N*logN)
冒泡排序:有序时,我们有优化,一趟比较下来没有发生交换,所以终止后面的排序,但是第一趟的相邻两个元素都发生了比较,比较了N次,所以最好时间复杂度为O(N),最坏,逆序,等差数列求和O(N^2)
快速排序:最好:每次找到的key都在中间,所以刚好是一个满二叉树,高度为logN,每层比较N次,总共比较N*logN次,所以最好为O(N*logN)
最坏:一个有序数组,每次找的key都在最左边,总共N层,比较等差数列求和次,所以最坏为O(N^2)
归并排序:最好最坏都是O(N*logN)只有快速排序和归并排序他们俩才会消耗额外额空间,因为递归要频繁的消耗栈帧,且快排非递归实现时运用了栈的数据结构。
好了,到此常见的排序算法我们已经全部学写完成了,排序算法是面试中的重点,大家一定要掌握。
好了,本期的内容到此结束^_^
相关文章:

数据结构之归并排序及排序总结
目录 归并排序 归并排序的时间复杂度 排序的稳定性 排序总结 归并排序 归并排序大家只需要掌握其递归方法即可,非递归方法由于在某些特殊场景下边界难控制,我们一般很少使用非递归实现归并排序。那么归并排序的递归方法我们究竟是怎样实现呢ÿ…...
仿windows12网盘,私有云盘部署教程,支持多种网盘
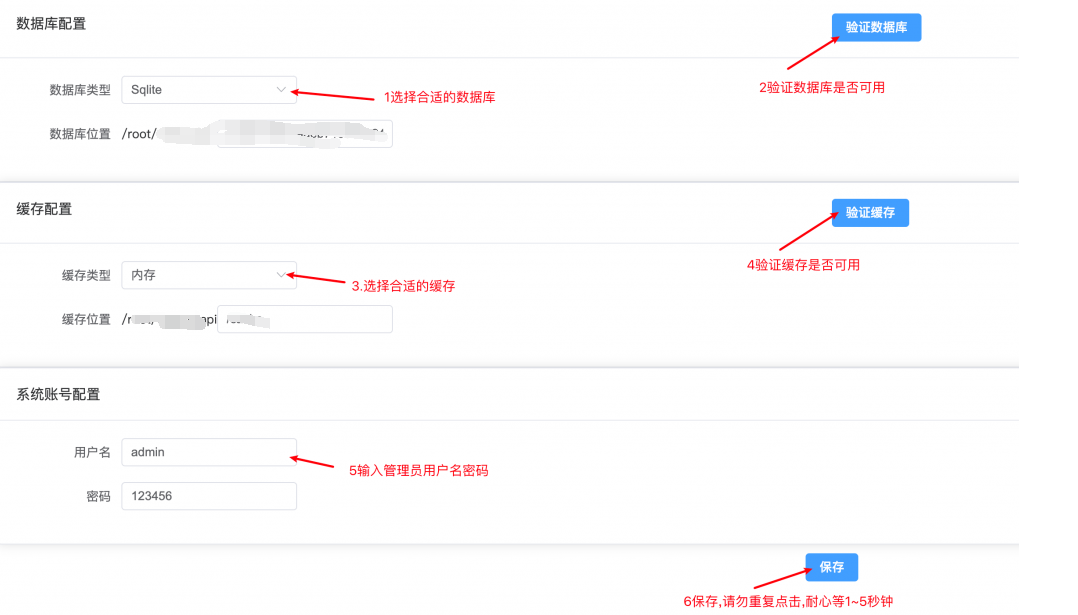
仿windows12网盘,私有云盘部署教程,支持多种网盘 资源宝分享:www.httple.net 视频教程:https://www.bilibili.com/video/BV1m64y1G7Bq/ 宝塔部署方式: 1.验证是否安装jdk,没有安装请看安装教程 推荐安装jdk8(注意您…...

深度学习 时间序列回归学习笔记
目录 常用的深度学习时间序列回归模型: ARIMA模型 ETS模型 效果评估...

【postgresql】ERROR: INSERT has more expressions than target columns
执行下面sql insert into apply_account_cancellation3 select * from pply_account_cancellation; 返回下面错误信息 insert into apply_account_cancellation3 select * from apply_account_cancellation > ERROR: INSERT has more expressions than target colu…...

Android Kotlin语言下的文件存储
目录 将数据存储到文件中 创建文件和保存数据 读取文件 SharedPreferences存储 存储数据到SharedPreferences中 Context类中的getSharedPreferences()方法 Activity类中的getPreferences()方法 从SharedPreferences中读取数据 SQLite数据库存储 创建数据库 调用数据…...

Verilog 入门(八)(验证)
文章目录 编写测试验证程序波形产生值序列重复模式 测试验证程序实例从文本文件中读取向量实例:时序检测器 测试验证程序用于测试和验证设计方法的正确性。Verilog 提供强有力的结构来说明测试验证程序。 编写测试验证程序 测试验证程序有三个主要目的:…...
)
vue3 vue-router 导航守卫 (五)
在Vue 3中,导航守卫仍然是一个重要的概念,用于在路由切换时执行一些特定的逻辑。Vue Router提供了多个导航守卫,包括全局守卫、路由独享守卫和组件内守卫。可以在路由切换时执行一些特定的逻辑,例如身份验证、权限控制、数据加载等…...

Git命令---查看远程仓库
介绍 使用git命令查看绑定的远程仓库。 命令 git remote -v...
12.8作业
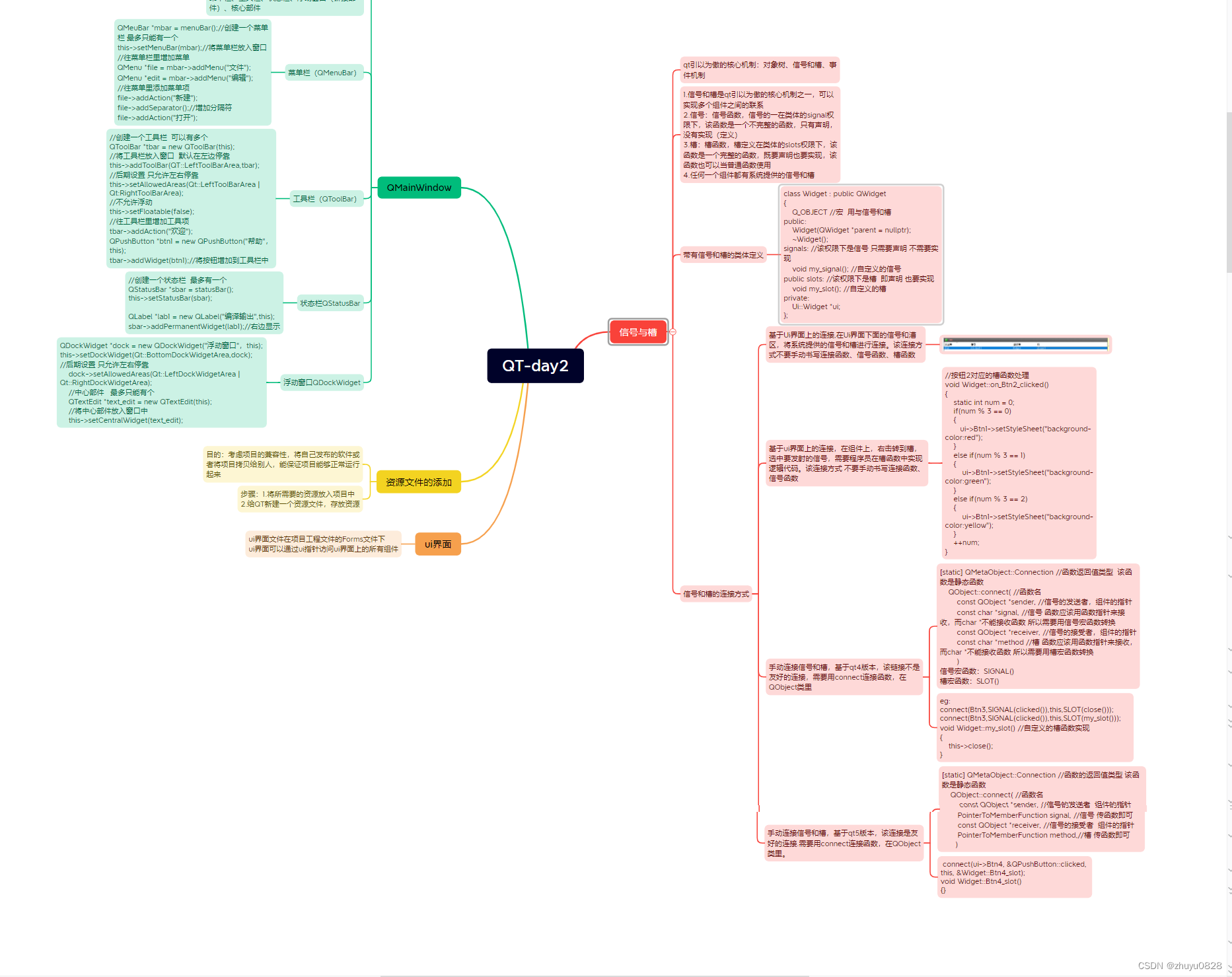
1. 使用手动连接,将登录框中的取消按钮使用qt4版本的连接到自定义的槽函数中,在自定义的槽函数中调用关闭函数 将登录按钮使用qt5版本的连接到自定义的槽函数中,在槽函数中判断ui界面上输入的账号是否为"admin",密码是…...

算法:有效的括号(入栈出栈)
时间复杂度 O(n) 空间复杂度 O(n∣Σ∣),其中 Σ 表示字符集,本题中字符串只包含 6 种括号 /*** param {string} s* return {boolean}*/ var isValid function(s) {const map {"(":")","{":"}","["…...

vxworks常用的指令归纳
目的:方便自己查阅 tftpboot 0x10000000 vxworks bootelf 0x10000000 ifconfig "gem0 dowm" ifconfig "gem0 inet 192.168.0.81" ifconfig "gem0 lladdr 01:02:03:04:05:06:07" ifconfig "gem0 up" ld 0,1,"…...

线性回归实战
3.1 使用正规方程进行求解 3.1.1 简单线性回归 公式 : y w x b y wx b ywxb 一元一次方程,在机器学习中一元表示一个特征,b表示截距,y表示目标值。 使用代码进行实现: 导入包 import numpy as np import matp…...

stm32 使用18B20 测试温度
用18b20 测试温度是非常常用的,不过18B20的调试不是这么容易的,有些内容网上很多的,不再重复说了,我先把波形说一下,再说程序部分: 整个都温度数据的顺序是: 1.700uS的低电平复位并测试18B20的…...
【Delphi】一个函数实现ios,android震动功能 Vibrate(包括3D Touch 中 Peek 震动等)
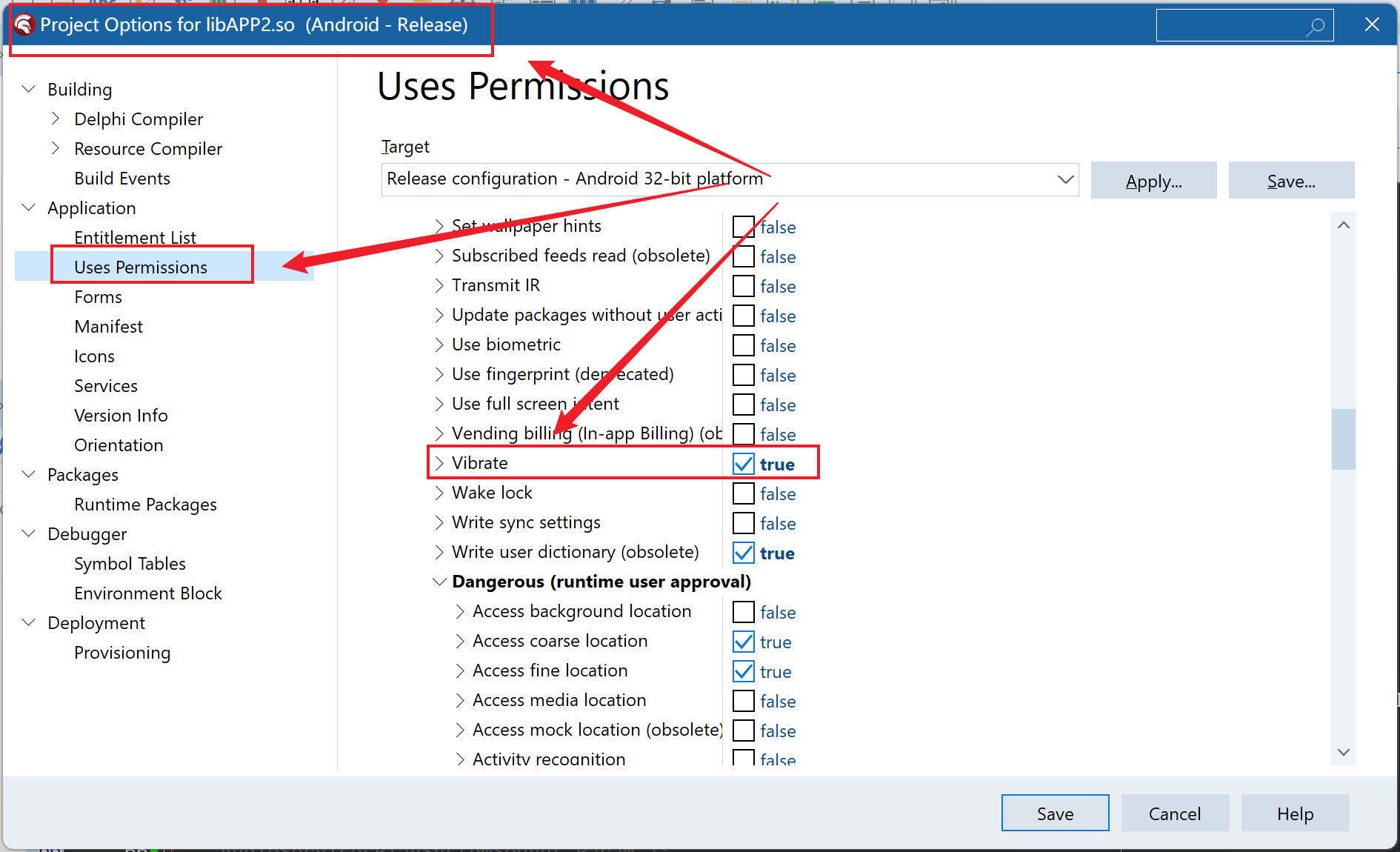
一、前言 我们在开发移动端APP的时候,有时可能需要APP能够提供震动功能,以便提醒操作者,特别是ios提供的3D Touch触感功能,操作者操作时会有触感震动,给操作者的感觉很友好。那么,在Delphi的移动端FMX开发中…...

国产Type-C PD芯片—接口快充取电芯片
常用USB PDTYPE-C受电端,即设备端协议IC芯片(PD Sink,也叫PD诱骗芯片),诱导取电芯片。 产品介绍 LDR6328: ◇ 采用 SOP-8 封装 ◇ 兼容 USB PD 3.0 规范,支持 USB PD 2.0 ◇ 兼容 QC 3.0 规范&#x…...
)
pytorch学习6-非线性变换(ReLU和sigmoid)
系列文章目录 pytorch学习1-数据加载以及Tensorboard可视化工具pytorch学习2-Transforms主要方法使用pytorch学习3-torchvisin和Dataloader的使用pytorch学习4-简易卷积实现pytorch学习5-最大池化层的使用pytorch学习6-非线性变换(ReLU和sigmoid)pytorc…...

详解Keras3.0 Models API: Whole model saving loading
1、save方法 Model.save(filepath, overwriteTrue, **kwargs) 将模型另存为.keras文件 参数说明 filepath: 保存模型的路径。必须以.keras结尾overwrite:布尔值,表示是否覆盖已存在的文件。默认为 True,即覆盖已存在的文件。save_format…...
Spring Cloud Gateway 网关的基础使用
1. 什么是网关?网关有什么用? 在微服务架构中,网关就是一个提供统一访问地址的组件,它解决了内部微服务与外部的交互问题。网关主要负责流量的路由和转发,将外部请求引到对应的微服务实例上。同时提供身份认证、授权、…...
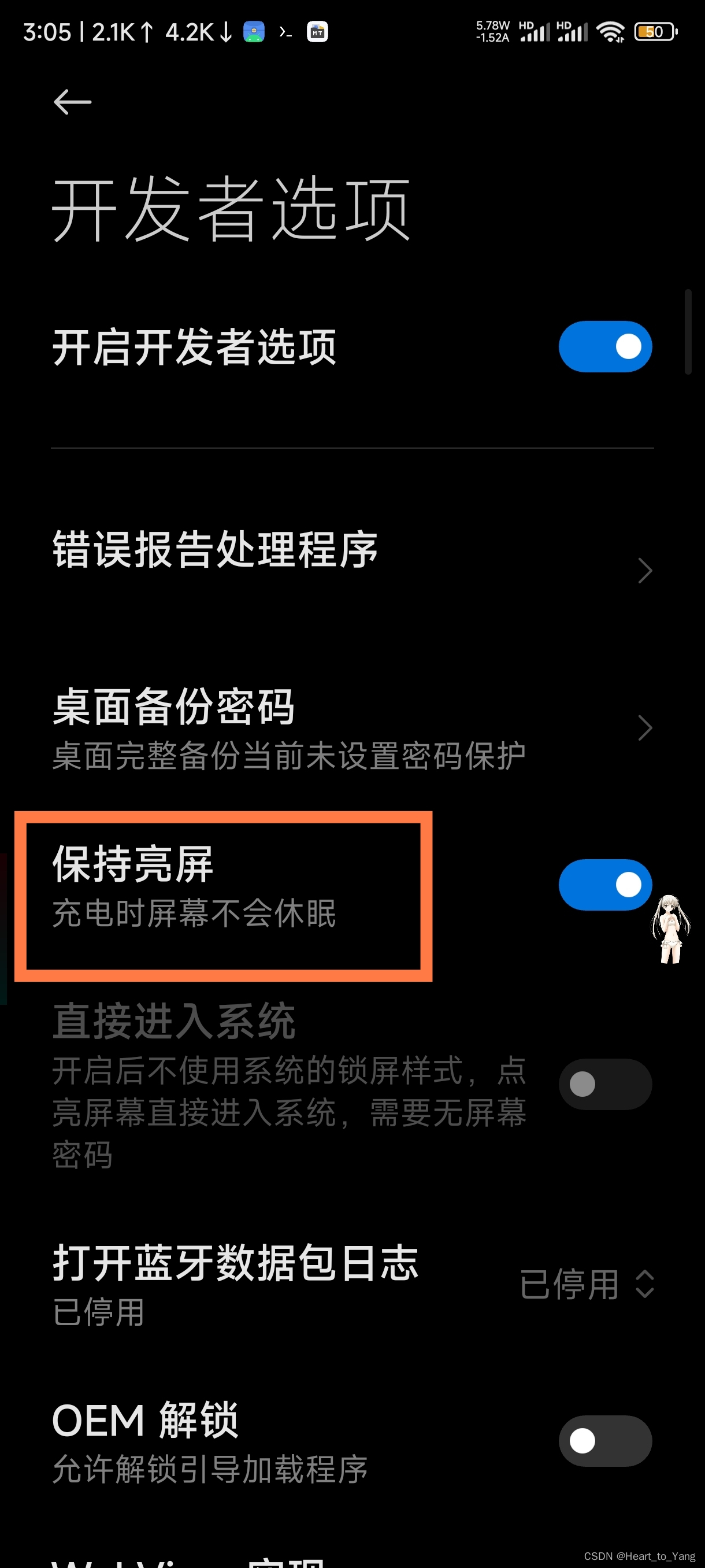
小米手机锁屏时间设置为永不休眠_手机不息屏_保持亮屏
环境:打开手机自带的锁屏时间设置发现没有 永不息屏的选项 原因:采用了三星OLED屏幕,所以根据OLED屏幕特性,这个是为了防止烧屏而特意设计的。非OLED机型支持设置“永不” 解决方案1:原生系统是支持永不锁屏的&#…...

lightdb plorasql集合类型新增可变数组
文章目录 背景集合类型可变数组可变数组示例 背景 在信创适配中,从Oracle迁移过来的存储过程使用到可变数组。因此在LightDB-X 23.4版本中对现有的集合类型进行了增强,添加了可变数组类型。 集合类型 在LightDB-X 23.4版本开始plorasql支持的集合类型…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
