机器学习-逻辑回归
一、引言
逻辑回归(Logistic Regression)是一种广泛应用于分类问题的监督学习算法。尽管名字中含有“回归”二字,但这并不意味着它用于解决回归问题。相反,逻辑回归专注于解决二元或多元分类问题,如邮件是垃圾邮件还是非垃圾邮件,一个交易是欺诈还是合法等。
逻辑回归源于统计学,旨在模拟一个因变量和一个或多个自变量之间的关系。与线性回归不同,逻辑回归并不直接预测数值,而是估计样本属于某一类别的概率。这通常通过Sigmoid函数(或对数几率函数)来实现,该函数能够将任何实数映射到0和1之间。
为了理解这种概率模型的重要性,我们可以考虑一下现代应用的复杂性。从金融风险评估、医疗诊断,到自然语言处理和图像识别,逻辑回归都找到了广泛的应用。它之所以受欢迎,一方面是因为其模型简单,易于理解和解释;另一方面是因为它在处理大量特征或者处理非线性关系时也具有很高的灵活性。
逻辑回归的算法实现通常基于最大似然估计(Maximum Likelihood Estimation, MLE),这是一种针对模型参数进行估计的优化算法。通过优化损失函数,算法试图找到最有可能解释观测数据的模型参数。
虽然逻辑回归在许多方面都很优秀,但它也有其局限性。例如,它假定因变量和自变量之间存在线性关系,这在某些复杂场景下可能不成立。然而,通过特征工程和正则化等手段,这些问题往往可以得到缓解。
总体而言,逻辑回归是机器学习领域中不可或缺的工具,其背后的数学原理和实际应用都值得深入研究。通过本文,我们将深入探讨逻辑回归的各个方面,以期提供一个全面、深入且易于理解的视角。
二、逻辑回归基础
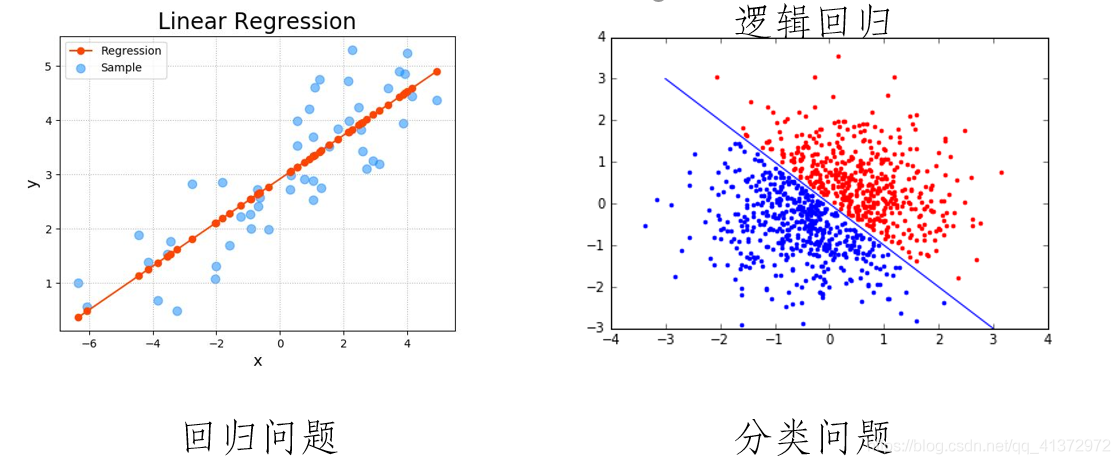
逻辑回归是一种针对分类问题的监督学习模型。它起源于统计学,尤其是当我们希望预测一个二元输出时,逻辑回归成为一个非常实用的工具。
从线性回归到逻辑回归
逻辑回归的思想是基于线性回归的,但有几个关键的不同点。在线性回归中,我们试图拟合一个线性方程来预测一个连续的输出值。然而,在逻辑回归中,我们不是直接预测输出值,而是预测输出值属于某一特定类别的概率。
举例:医学检测
假设我们有一个用于检测某种疾病(如糖尿病)的医学测试。在这种情况下,线性回归可能会预测一个人患疾病的程度或严重性。但逻辑回归更进一步:它会预测一个人患疾病的概率,并根据这个概率进行分类——例如,概率大于0.5则判断为阳性。
Sigmoid 函数
逻辑回归中最关键的组成部分是 Sigmoid(或称为 logistic)函数。这个函数接受任何实数作为输入,并将其映射到0和1之间,使其可以解释为概率。

举例:考试成绩与录取概率
考虑一个学生根据其考试成绩被大学录取的例子。线性回归可能会直接预测录取概率,但数值可能会超过[0,1]的范围。通过使用 Sigmoid 函数,我们可以确保预测值始终在合适的范围内。
损失函数
在逻辑回归中,最常用的损失函数是交叉熵损失(Cross-Entropy Loss)。该损失函数度量模型预测的概率分布与真实概率分布之间的差距。

举例:垃圾邮件分类
假设我们正在构建一个垃圾邮件过滤器。对于每封邮件,模型会预测这封邮件是垃圾邮件的概率。如果一封实际上是垃圾邮件(y=1)的邮件被预测为非垃圾邮件(yhat约等于0),损失函数的值会非常高,反之亦然。
优点与局限性
优点
- 解释性强:逻辑回归模型易于理解和解释。
- 计算效率:模型简单,训练和预测速度快。
- 概率输出:提供预测类别的概率,增加了解释性。
局限性
- 线性边界:逻辑回归假设数据是线性可分的,这在某些复杂场景下可能不成立。
- 特征选择:逻辑回归对于不相关的特征和特征之间的相互作用比较敏感。
通过这个章节,我们可以看到逻辑回归在简洁性和解释性方面有着显著的优点,但同时也存在一定的局限性。
三、数学原理

理解逻辑回归背后的数学原理是掌握这一算法的关键。这部分将深入解析逻辑回归的数学结构,包括概率模型、损失函数优化和特征选择。
概率模型

举例:信用卡交易
想象你正在开发一个用于检测信用卡欺诈交易的模型。在这种情况下,(X) 可能包括交易金额、地点、时间等特征,模型会输出这笔交易是欺诈交易的概率。
损失函数与最大似然估计
最常用于逻辑回归的损失函数是交叉熵损失。这其实是最大似然估计(MLE)在逻辑回归中的具体应用。

举例:电子邮件分类
假设你正在构建一个电子邮件分类器来区分垃圾邮件和正常邮件。使用交叉熵损失函数,你可以通过最大化似然函数来“教”模型如何更准确地进行分类。
梯度下降优化

举例:股票价格预测
虽然逻辑回归通常不用于回归问题,但梯度下降的优化算法在很多其他类型的问题中也是通用的。例如,在预测股票价格时,同样可以使用梯度下降来优化模型参数。
特征选择与正则化
特征选择在逻辑回归中非常重要,因为不相关或冗余的特征可能会导致模型性能下降。正则化是一种用于防止过拟合的技术,常见的正则化方法包括 L1 正则化和 L2 正则化。

举例:房价预测
在房价预测模型中,可能有很多相关和不相关的特征,如面积、地段、周围学校数量等。通过使用正则化,你可以确保模型在拟合这些特征时不会过于复杂,从而提高模型的泛化能力。
通过本章的讨论,我们不仅深入了解了逻辑回归的数学基础,还通过具体的例子和应用场景,让这些看似复杂的数学概念更加贴近实际,易于理解。这有助于我们在实际应用中更加灵活地使用逻辑回归,以解决各种分类问题。
四、实战案例

实战是学习逻辑回归的最佳方式。在这一部分,我们将使用Python和PyTorch库来实现一个完整的逻辑回归模型。我们将使用经典的鸢尾花(Iris)数据集,该数据集包括四个特征:萼片长度、萼片宽度、花瓣长度、花瓣宽度,以及一个标签,用于区分三种不同类型的鸢尾花。
数据准备
首先,我们需要加载和准备数据。
# 导入所需库
import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split# 加载数据
iris = load_iris()
X, y = iris.data, iris.target# 由于逻辑回归是二分类模型,我们只取其中两类数据
X, y = X[y != 2], y[y != 2]# 数据分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 转换为PyTorch张量
X_train = torch.FloatTensor(X_train)
X_test = torch.FloatTensor(X_test)
y_train = torch.LongTensor(y_train)
y_test = torch.LongTensor(y_test)
模型构建
接下来,我们定义逻辑回归模型。
class LogisticRegression(nn.Module):def __init__(self, input_dim):super(LogisticRegression, self).__init__()self.linear = nn.Linear(input_dim, 1)self.sigmoid = nn.Sigmoid()def forward(self, x):return self.sigmoid(self.linear(x))
模型训练
现在我们可以开始训练模型。
# 初始化模型、损失函数和优化器
model = LogisticRegression(X_train.shape[1])
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)# 训练模型
for epoch in range(1000):model.train()optimizer.zero_grad()# 前向传播outputs = model(X_train).squeeze()loss = criterion(outputs, y_train.float())# 反向传播和优化loss.backward()optimizer.step()if (epoch + 1) % 100 == 0:print(f'Epoch [{epoch+1}/1000], Loss: {loss.item()}')
模型评估
最后,我们用测试集来评估模型的性能。
# 测试模型
model.eval()
with torch.no_grad():test_outputs = model(X_test).squeeze()test_outputs = (test_outputs > 0.5).long()accuracy = (test_outputs == y_test).float().mean()print(f'Accuracy: {accuracy.item()}')相关文章:

机器学习-逻辑回归
一、引言 逻辑回归(Logistic Regression)是一种广泛应用于分类问题的监督学习算法。尽管名字中含有“回归”二字,但这并不意味着它用于解决回归问题。相反,逻辑回归专注于解决二元或多元分类问题,如邮件是垃圾邮件还是…...

Edge调用Aria2下载
一、准备工作 1、Edge浏览器:Windows系统自带或点击下载; 2、Aria2 gui:点击github下载或自行搜索下载其他版本; 二、启动Aria2 gui 解压下载的Aria2 gui到任意目录,点击“Aria2c启动器”或“AriaNg启动器”皆可。…...

解密QQ号——C语言
题目: 有一串已加密的数字“6 3 1 7 5 8 9 2 4”解密规则:首先将第1个数字删除,紧接着将第2个数字放到这串数字的末尾,再将第3个数字删除并将第4个数字放到这串数字的末尾,再将第5个数删除 代码实现: #inc…...
三、jvm中的对象及引用
一、对象在jvm的创建过程 检查加载-->分配内存-->内存空间初始化-->设置-->对象初始化 1) 检查加载 首先检查这个指令的参数是否能在常量池中定位到一个类的符号引用,并且检查类是否已经被加载、解析和初始化过。 虚拟机遇到一条 new 指令时…...
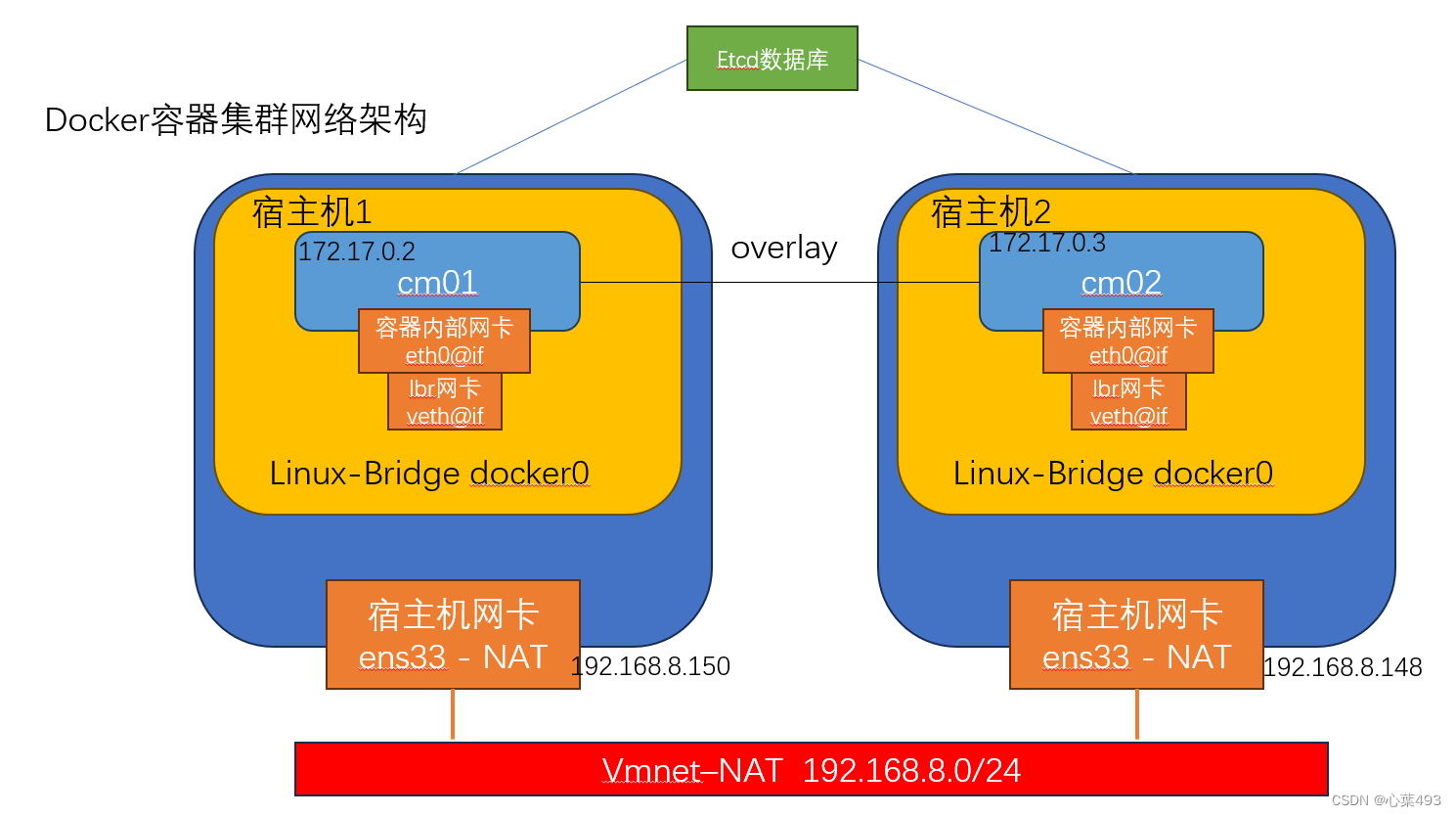
Docker网络架构介绍
本文主要介绍了Docker容器的单机网络架构与集群网络架构,辅以演示,并简单介绍了网络管理中的命令。 前文: Docker的安装与简单操作命令-CSDN博客 docker网络原理介绍 与ovs类似,docker容器采用veth-pair linux bridge (虚拟交…...

Android studio新版本aar包导入项目中配置
目录 1、so、aar导入在项目build.gradle中配置 2、新版本迁移到setting.grade配置 1、so、aar导入在项目build.gradle中配置 repositories {flatDir {dirs libs} }2、新版本迁移到setting.grade配置 flatDir {dirs libs } 如下图所示 pluginManagement {repositories {gra…...
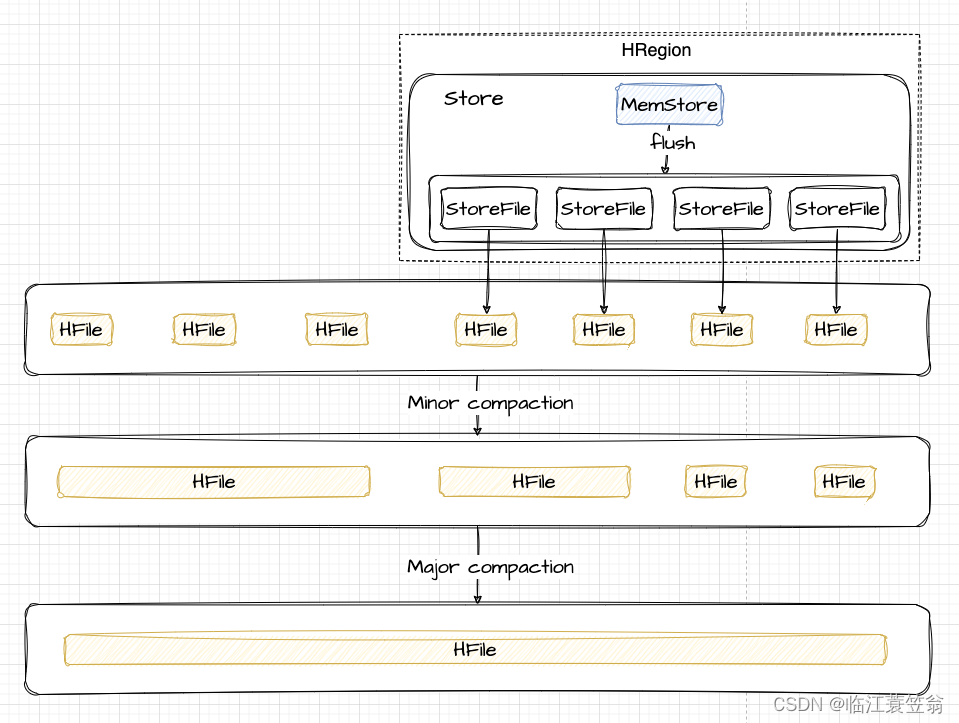
HBase-架构与设计
HBase架构与设计 一、背景二、HBase概述1.设计特点2.适用场景2.1 海量数据2.2 稀疏数据2.3 多版本数据2.4 半结构或者非结构化数据 三、数据模型1.表逻辑结构2.RowKey3.Column Family4.TimeStamp5.存储结构 四、HBase架构图1.Client2.Zookeeper3.HMaster4.HRegionServer5.HRegi…...

SpringBoot基础系列:工具类使用
断言 Assert // 要求参数 object 必须为非空(Not Null),否则抛出异常,不予放行 // 参数 message 参数用于定制异常信息。 void notNull(Object object, String message) // 要求参数必须空(Null)ÿ…...

使用 nohup java - jar 不输出日志
要在使用nohup java -jar命令时不输出日志,可以将标准输出和标准错误输出重定向到特殊设备文件/dev/null。这样做将会丢弃所有的输出。 以下是在Linux中使用nohup java -jar命令并禁止输出日志的示例: 复制代码 nohup java -jar your-application.jar …...
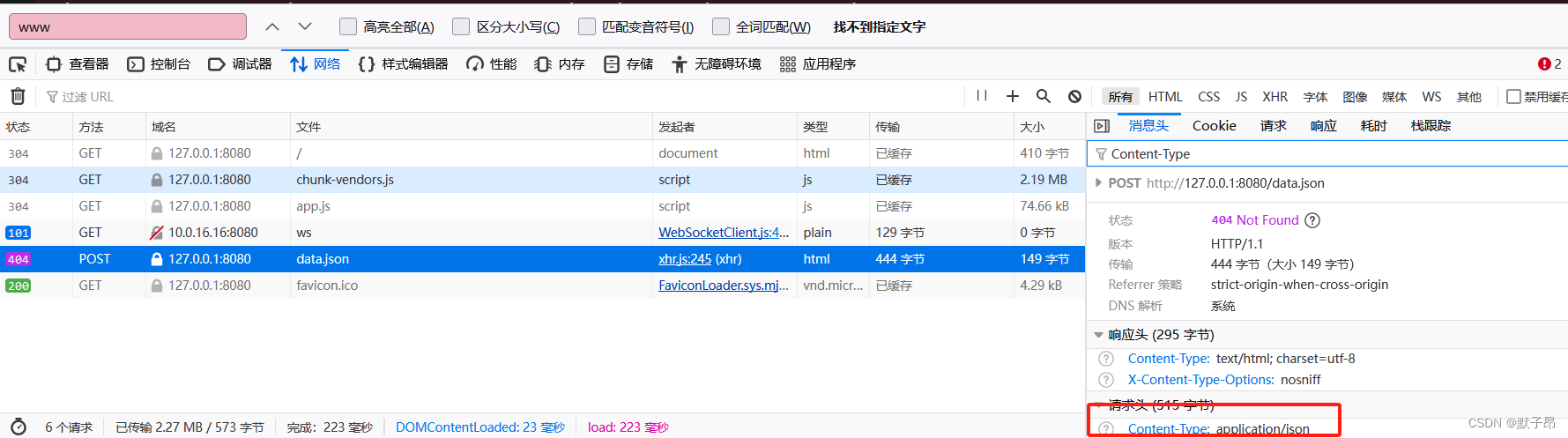
前端开发学习 (五) 生命周期函数、Ajax请求
关于vue实例的声明周期,从Vue实例创建、运行、到销毁期间,总是伴随着各种各样的事件,这些事件,统称为生命周期 (https://cn.vuejs.org/v2/guide/instance.html#实例生命周期 ) 而声明周期勾子就是生命周期…...
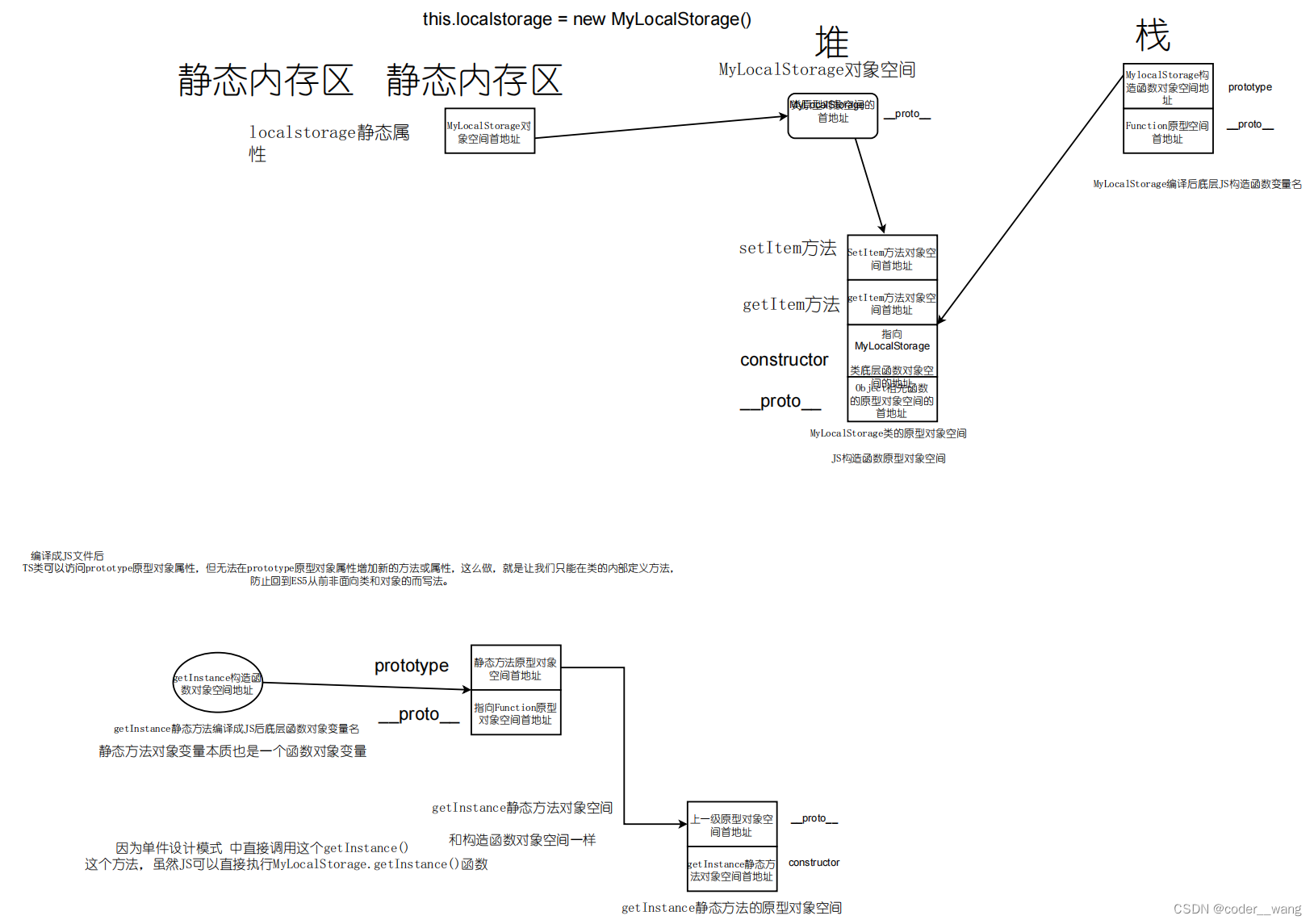
TypeScript中的单件设计模式
基本概念 (1) 了解设计模式 设计模式通俗的讲,就是一种更好的编写代码方案,打个比喻:从上海到武汉,你可以选择做飞机,做轮船,开车,骑摩托车多种方式,把出行…...

【无标题】安装环境
这里写目录标题 清华镜像加速 安装cuda11.3 PyTorch 1.10.1https://pytorch.org/get-started/previous-versions/[如果没有可以点Previous pyTorch Versions,这里面有更多的更早的版本](https://pytorch.org/get-started/locally/) 复制非空文件夹cp: -r not specif…...

一. 初识数据结构和算法
数据结构与算法是一个达到高级程序员的敲门砖。当你脱离了语言的应用层面,去思考他的设计层面时,你就依旧已经开始初识数据结构与算法了 数据结构 什么是数据结构 对于数据结构的定义官方并没有统一的解释,在各个百科以及算法的书中…...

qt 使用百度在线地图 方法1
在使用Qt和百度在线地图时,你需要从百度地图开放平台获取API密钥,并使用该密钥在Qt应用程序中集成百度地图。以下是一个简单的示例,演示了如何在Qt中使用百度在线地图: 1,首先,从百度地图开放平台获取API密…...
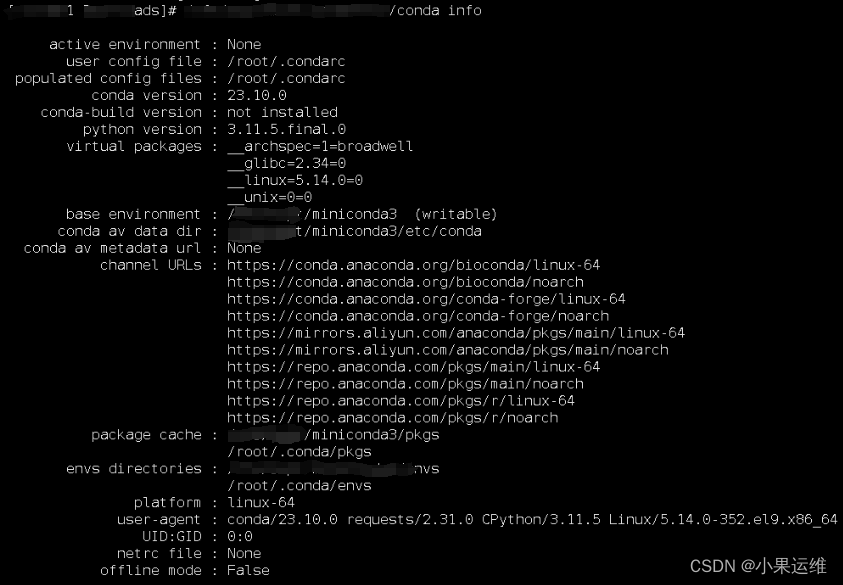
轻快小miniconda3在linux下的安装配置-centos9stream-Miniconda3 Linux 64-bit
miniconda与anaconda的区别: Miniconda 和 Anaconda 是用于管理环境和安装软件包的 Python 发行版。它们之间的主要区别在于以下几点: 1. 安装内容和大小: Anaconda: Anaconda 是一个完整的 Python 数据科学平台,包含…...
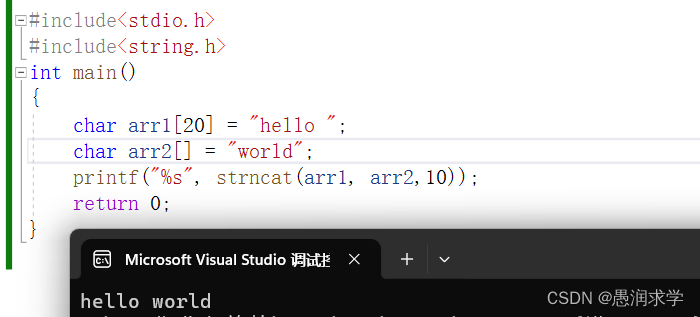
C语言——字符函数和字符串函数(一)
📝前言: 这篇文章对我最近学习的有关字符串的函数做一个总结和整理,主要讲解字符函数和字符串函数(strlen,strcpy和strncpy,strcat和strncat)的使用方法,使用场景和一些注意事项&…...
15.Java程序设计-基于SSM框架的微信小程序校园求职系统的设计与实现
摘要: 本研究旨在设计并实现一款基于SSM框架的微信小程序校园求职系统,以提升校园求职流程的效率和便捷性。通过整合微信小程序平台和SSM框架的优势,本系统涵盖了用户管理、职位发布与搜索、简历管理、消息通知等多个功能模块,为…...
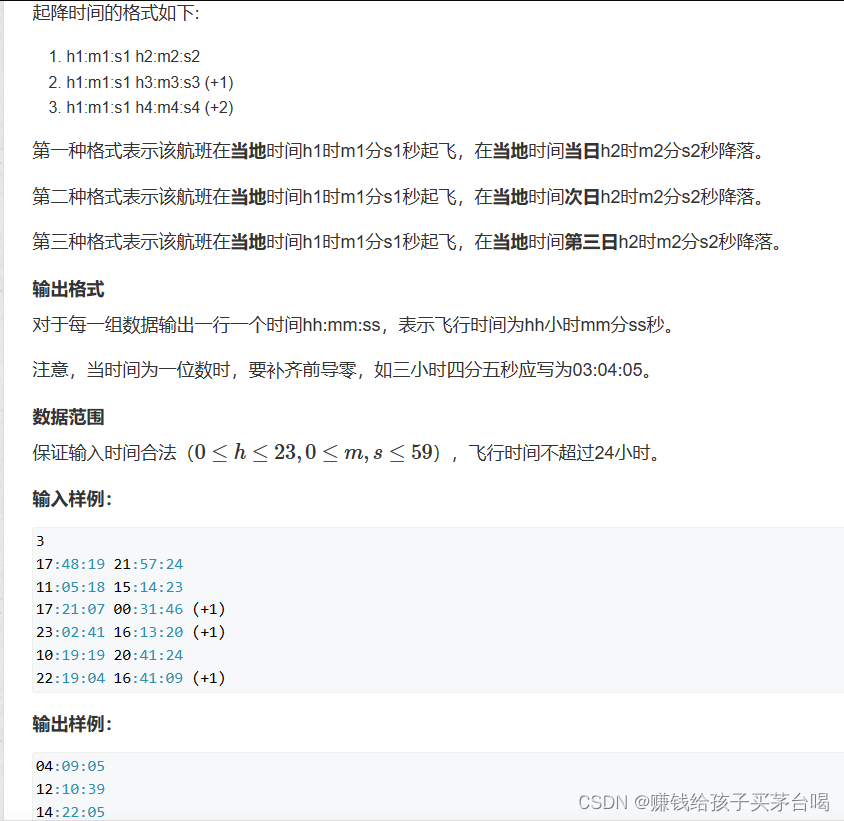
蓝桥杯航班时间
蓝桥杯其他真题点这里👈 //飞行时间 - 时差 已过去的时间1 //飞行时间 时差 已过去的时间2 //两个式子相加会发现 飞行时间 两段时间差的和 >> 1import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader;public cl…...

openEuler学习05-kernel升级
周末没事,尝试下openEuler的kernel升级 [rootlocalhost ~]# more /etc/os-release NAME"openEuler" VERSION"20.03 (LTS-SP3)" ID"openEuler" VERSION_ID"20.03" PRETTY_NAME"openEuler 20.03 (LTS-SP3)" ANSI_…...

Linux-centos上如何配置管理NFS服务器?
Linux/centos上如何配置管理NFS服务器? 1 NFS基础了解 NFS(Network File System)即文件操作系统;NFS允许网络中不同计算机相互之间共享资源。 1.1 NFS概述 1980年由SUN发展出来的在UNIX&Linux系统间实现文件共享的一种方法…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...
