【数据挖掘】国科大苏桂平老师数据库新技术课程作业 —— 第二次作业
1
设 F = { A B → C , B → D , C D → E , C E → G H , G → A } F=\{AB\rightarrow C,B\rightarrow D, CD\rightarrow E, CE\rightarrow GH, G\rightarrow A \} F={AB→C,B→D,CD→E,CE→GH,G→A},用推理的方法证明 F ∣ = A B → G F\;|=AB\rightarrow G F∣=AB→G。
① 已知 B → D B\rightarrow D B→D,则 A B → A D AB\rightarrow AD AB→AD(增广律)
② 已知 A B → A D AB\rightarrow AD AB→AD,则 A B → D AB\rightarrow D AB→D (分解规则)
③ 已知 A B → C AB\rightarrow C AB→C, A B → D AB\rightarrow D AB→D,则 A B → C D AB\rightarrow CD AB→CD (合成规则)
④ 已知 A B → C D AB\rightarrow CD AB→CD, C D → E CD\rightarrow E CD→E,则 A B → E AB\rightarrow E AB→E (传递律)
⑤ 已知 A B → E AB\rightarrow E AB→E, A B → C AB\rightarrow C AB→C,则 A B → C E AB\rightarrow CE AB→CE (合成规则)
⑥ 已知 C E → G H CE\rightarrow GH CE→GH,则 C E → G CE\rightarrow G CE→G (分解规则)
⑦ 已知 A B → C E AB\rightarrow CE AB→CE, C E → G CE\rightarrow G CE→G,则 A B → G AB\rightarrow G AB→G (传递律)
注意区别”传递律“与”传递函数依赖“。
2
设关系模式 R ( A , B , C , D ) R(A,B,C,D) R(A,B,C,D),其函数依赖集为 F = { A → B , B → C , A → D , D → C } F=\{A\rightarrow B, B\rightarrow C, A\rightarrow D, D\rightarrow C\} F={A→B,B→C,A→D,D→C}, R R R 的一个分解 ρ = { R 1 ( A , B ) , R 2 ( A , C ) , R 3 ( A , D ) } \rho = \{R_1(A,B), R_2(A,C), R_3(A,D)\} ρ={R1(A,B),R2(A,C),R3(A,D)}。
(1)求 F F F 在 ρ \rho ρ 的每个模式上的投影
F F F 在关系模式 R 1 ( A , B ) R_1(A,B) R1(A,B) 上的投影为 { A → B } \{A\rightarrow B\} {A→B}; F F F 在关系模式 R 2 ( A , C ) R_2(A,C) R2(A,C) 上的投影为 { A → C } \{A\rightarrow C\} {A→C}; F F F 在关系模式 R 3 ( A , D ) R_3(A,D) R3(A,D) 上的投影为 { A → D } \{A\rightarrow D\} {A→D}。
(2) ρ \rho ρ 相对于 F F F 是无损连接吗?
| A | B | C | D |
| a1 | a2 | b13→a3 | b14→a4 |
| a1 | b22→a2 | a3 | b24→a4 |
| a1 | b32→a2 | b33→a3 | a4 |
其中,红色对应 F F F 中的 A → B A\rightarrow B A→B,蓝色对应 F F F 中的 B → C B\rightarrow C B→C,绿色对应 F F F 中的 A → D A\rightarrow D A→D,此时 F F F 中的 D → C D\rightarrow C D→C 不影响表格。
由于存在某一行全为 a a a,所以 ρ \rho ρ 相对于 F F F 是无损连接。
当分解只包括两个关系模式时,可以使用定理”分解 ρ = { R 1 , R 2 } \rho=\{R_1, R_2\} ρ={R1,R2},若 F ∣ = ( R 1 ∩ R 2 ) → ( R 1 − R 2 ) F|=(R_1\cap R_2)\rightarrow (R_1-R_2) F∣=(R1∩R2)→(R1−R2) 或者 F ∣ = ( R 1 ∩ R 2 ) → ( R 2 − R 1 ) F|=(R_1\cap R_2)\rightarrow (R_2-R_1) F∣=(R1∩R2)→(R2−R1),则 ρ \rho ρ 具有无损连接性“判断是否为无损连接。
(3) ρ \rho ρ 保持函数依赖吗?
A + = A B C D A^+=ABCD A+=ABCD, B + = B C B^+=BC B+=BC, C + = C C^+=C C+=C, D + = C D D^+=CD D+=CD。
考察 A → B A\rightarrow B A→B, A ⊂ R 1 A\subset R_1 A⊂R1, A + ∩ R 1 − A = { B } A^+ \cap R_1-A=\{B\} A+∩R1−A={B}, G = { A → B } G = \{A\rightarrow B\} G={A→B};同理 A ⊂ R 2 A\subset R_2 A⊂R2, G = G ∪ { A → C } G = G\cup \{A\rightarrow C\} G=G∪{A→C}, A ⊂ R 3 A\subset R_3 A⊂R3, G = G ∪ { A → D } G = G\cup \{A\rightarrow D\} G=G∪{A→D}。 G = { A → B , A → C , A → D } G = \{A\rightarrow B,A\rightarrow C,A\rightarrow D\} G={A→B,A→C,A→D}。
考察 B → C B\rightarrow C B→C, B ⊂ R 1 B\subset R_1 B⊂R1, B + ∩ R 1 − B = ϕ B^+\cap R_1 - B = \phi B+∩R1−B=ϕ, G G G 不变。
考察 A → D A\rightarrow D A→D 类似于 A → B A\rightarrow B A→B, G = G ∪ { A → B , A → C , A → D } G = G\cup \{A\rightarrow B,A\rightarrow C,A\rightarrow D\} G=G∪{A→B,A→C,A→D}, G G G 不变。
考察 D → C D\rightarrow C D→C, D ⊂ R 3 D\subset R_3 D⊂R3, D + ∩ R 1 − D = ϕ D^+\cap R_1 - D = \phi D+∩R1−D=ϕ, G G G 不变。
最终 G = { A → B , A → C , A → D } G = \{A\rightarrow B,A\rightarrow C,A\rightarrow D\} G={A→B,A→C,A→D}。
显然 G G G 不蕴含 F F F 中的函数依赖 B → C B\rightarrow C B→C 和 D → C D\rightarrow C D→C,所以 ρ \rho ρ 没有保持函数依赖。
3
1NF、2NF、3NF 和 BCNF 的定义:
1NF:如果一个关系模式 R R R 中的每个属性 A A A 的域值都是原子的,即属性值是不可再分的,则关系模式 R R R 属于第一范式,简记为 R ∈ 1 N F R\in {\rm 1NF} R∈1NF。
2NF:如果 R ∈ 1 N F R∈{\rm 1NF} R∈1NF 且所有的非主属性完全依赖于 R R R 的每个键,则 R ∈ 2 N F R∈{\rm 2NF} R∈2NF。
3NF:如果 R ∈ 1 N F R\in {\rm 1NF} R∈1NF 且在 R R R 中没有非主属性传递依赖于 R R R 的键,则 R ∈ 3 N F R∈\rm 3NF R∈3NF。
BCNF:如果 R ∈ 1 N F R∈\rm 1NF R∈1NF 且 R R R 中没有任何属性传递依赖于 R R R 的任何一个键,则 R ∈ B o y c e − C o d d R∈\rm Boyce-Codd R∈Boyce−Codd 范式(BCNF)。
注意,传递依赖的定义:设关系模式 R R R, X X X、 Y Y Y、 Z Z Z 是 R R R 的属性子集,若函数依赖 X → Y X\rightarrow Y X→Y, Y ↛ X Y\nrightarrow X Y↛X, Y → z Y\rightarrow z Y→z,则有 X → Z X\rightarrow Z X→Z。
指出下列关系模式是第几范式,并说明理由。
(1) R ( A , B , C ) R(A,B,C) R(A,B,C),其函数依赖集为 F = { B → C , A C → B } F=\{B\rightarrow C, AC\rightarrow B\} F={B→C,AC→B}
确定 R R R 的键, A + = A A^+ = A A+=A, B + = B C B^+ = BC B+=BC, C + = C C^+=C C+=C; ( A B ) + = A B C (AB)^+=ABC (AB)+=ABC, ( A C ) + = A B C (AC)^+=ABC (AC)+=ABC,所以键为 A B AB AB 和 A C AC AC。关系模式 R R R 无非主属性,因此 R ∈ 2 N F R\in \rm 2NF R∈2NF, R ∈ 3 N F R\in 3\rm NF R∈3NF。但是由于 A C → B AC\rightarrow B AC→B, B ↛ A C B\nrightarrow AC B↛AC, B → C B\rightarrow C B→C ,存在传递依赖,故 R ∉ B C N F R\notin \rm BCNF R∈/BCNF。
(2) R ( A , B , C ) R(A,B, C) R(A,B,C),其函数依赖集为 F = { A B → C } F=\{AB\rightarrow C\} F={AB→C}
( A B ) + = A B C (AB)^+ = ABC (AB)+=ABC,显然 R R R 的键为 A B AB AB,即 A A A 和 B B B 为主属性, C C C 为非主属性。 A B → C AB\rightarrow C AB→C, C C C 完全依赖于键 A B AB AB, R ∈ 2 N F R\in 2\rm NF R∈2NF。不存在传递依赖, R ∈ 3 N F R\in 3\rm NF R∈3NF, R ∈ B C N F R\in \rm BCNF R∈BCNF。
(3) R ( A , B , C ) R(A,B,C) R(A,B,C),其函数依赖集为 F = { A → B , A → C } F=\{A\rightarrow B, A\rightarrow C\} F={A→B,A→C}
R R R 的键为 A A A, A A A 为主属性, B B B 和 C C C 为非主属性。 B B B 和 C C C 完全依赖于 A A A, R ∈ 2 N F R\in \rm 2NF R∈2NF。不存在传递依赖,, R ∈ 3 N F R\in 3\rm NF R∈3NF, R ∈ B C N F R\in \rm BCNF R∈BCNF。
(4) R ( A , B , C , D ) R(A,B,C,D) R(A,B,C,D),其函数依赖集为 F = { A → C , A D → B } F=\{A\rightarrow C, AD\rightarrow B\} F={A→C,AD→B}
R R R 的键为 A D AD AD, A A A 和 D D D 为主属性, B B B 和 C C C 为非主属性。 B B B 完全依赖于键 A D AD AD,但是 C C C 部分依赖于键 A D AD AD,所以 R ∉ 2 N F R\notin 2\rm NF R∈/2NF。
(5) R ( A , B , C ) R(A,B,C) R(A,B,C),其函数依赖集为 F = { B → C , B → A , A → B C } F=\{B\rightarrow C, B\rightarrow A, A\rightarrow BC\} F={B→C,B→A,A→BC}
A + = B + = A B C A^+=B^+=ABC A+=B+=ABC,所以键为 A A A 和 B B B, C C C 为非主属性。根据分解规则可知 A → C A\rightarrow C A→C, C C C 完全依赖于 A A A,又 B → C B\rightarrow C B→C, C C C 完全依赖于 B B B,所以 R ∈ 2 N F R\in 2\rm NF R∈2NF。因为 A → B A\rightarrow B A→B, B → A B\rightarrow A B→A,尽管 A → C A\rightarrow C A→C(或 B → C B\rightarrow C B→C),但是不满足传递依赖的定义,所以不存在传递依赖,故 R ∈ 3 N F R\in 3\rm NF R∈3NF, R ∈ B C N F R\in \rm BCNF R∈BCNF。
相关文章:

【数据挖掘】国科大苏桂平老师数据库新技术课程作业 —— 第二次作业
1 设 F { A B → C , B → D , C D → E , C E → G H , G → A } F\{AB\rightarrow C,B\rightarrow D, CD\rightarrow E, CE\rightarrow GH, G\rightarrow A \} F{AB→C,B→D,CD→E,CE→GH,G→A},用推理的方法证明 F ∣ A B → G F\;|AB\rightarrow G F∣AB→…...
Qt + MySQL(简单的增删改查)
Qt编译MySql插件教程 帮助: SQL Programming QSqlDatabase 静态函数 1.drivers(),得到可以使用的数据库驱动名字的集合 [static] QStringList QSqlDatabase::drivers();2.addDatabase(),添加一个数据库实例 [static] QSqlDatabase QSql…...

postgresql设置免密登录
您提供的步骤描述了在 PostgreSQL 数据库环境中配置服务器间的 SSH 无密码登录和数据库用户认证的过程。这些步骤主要用于设置一个高可用性、负载平衡的数据库集群环境。让我们逐一解释这些步骤的目的和应用场景: 1. 启动 PostgreSQL 服务 systemctl start postgr…...
视频汇聚/音视频流媒体视频平台/视频监控EasyCVR分享页面无法播放,该如何解决?
国标GB28181安防视频监控/视频集中存储/云存储EasyCVR平台可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。平台既具备传统…...

机器学习-逻辑回归
一、引言 逻辑回归(Logistic Regression)是一种广泛应用于分类问题的监督学习算法。尽管名字中含有“回归”二字,但这并不意味着它用于解决回归问题。相反,逻辑回归专注于解决二元或多元分类问题,如邮件是垃圾邮件还是…...

Edge调用Aria2下载
一、准备工作 1、Edge浏览器:Windows系统自带或点击下载; 2、Aria2 gui:点击github下载或自行搜索下载其他版本; 二、启动Aria2 gui 解压下载的Aria2 gui到任意目录,点击“Aria2c启动器”或“AriaNg启动器”皆可。…...

解密QQ号——C语言
题目: 有一串已加密的数字“6 3 1 7 5 8 9 2 4”解密规则:首先将第1个数字删除,紧接着将第2个数字放到这串数字的末尾,再将第3个数字删除并将第4个数字放到这串数字的末尾,再将第5个数删除 代码实现: #inc…...
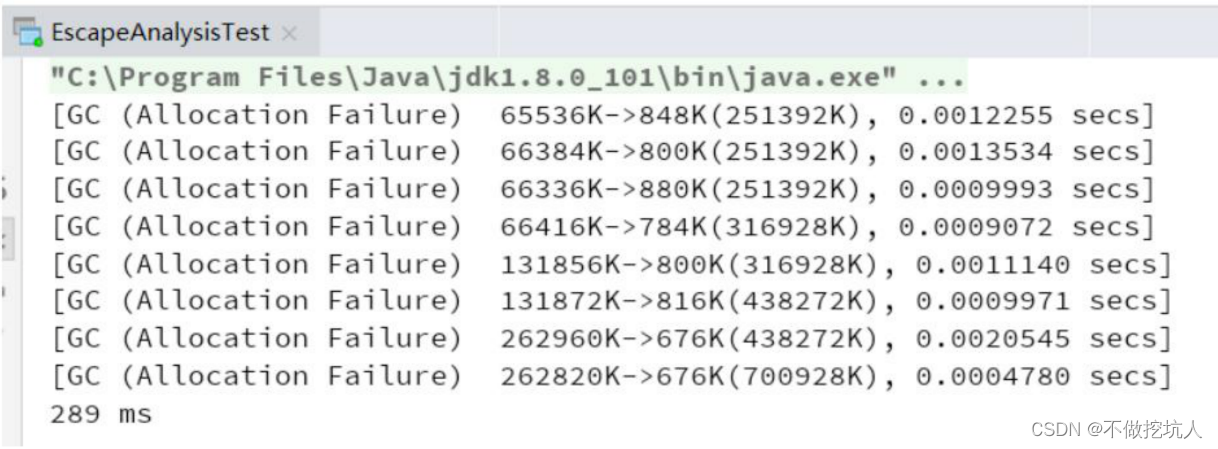
三、jvm中的对象及引用
一、对象在jvm的创建过程 检查加载-->分配内存-->内存空间初始化-->设置-->对象初始化 1) 检查加载 首先检查这个指令的参数是否能在常量池中定位到一个类的符号引用,并且检查类是否已经被加载、解析和初始化过。 虚拟机遇到一条 new 指令时…...
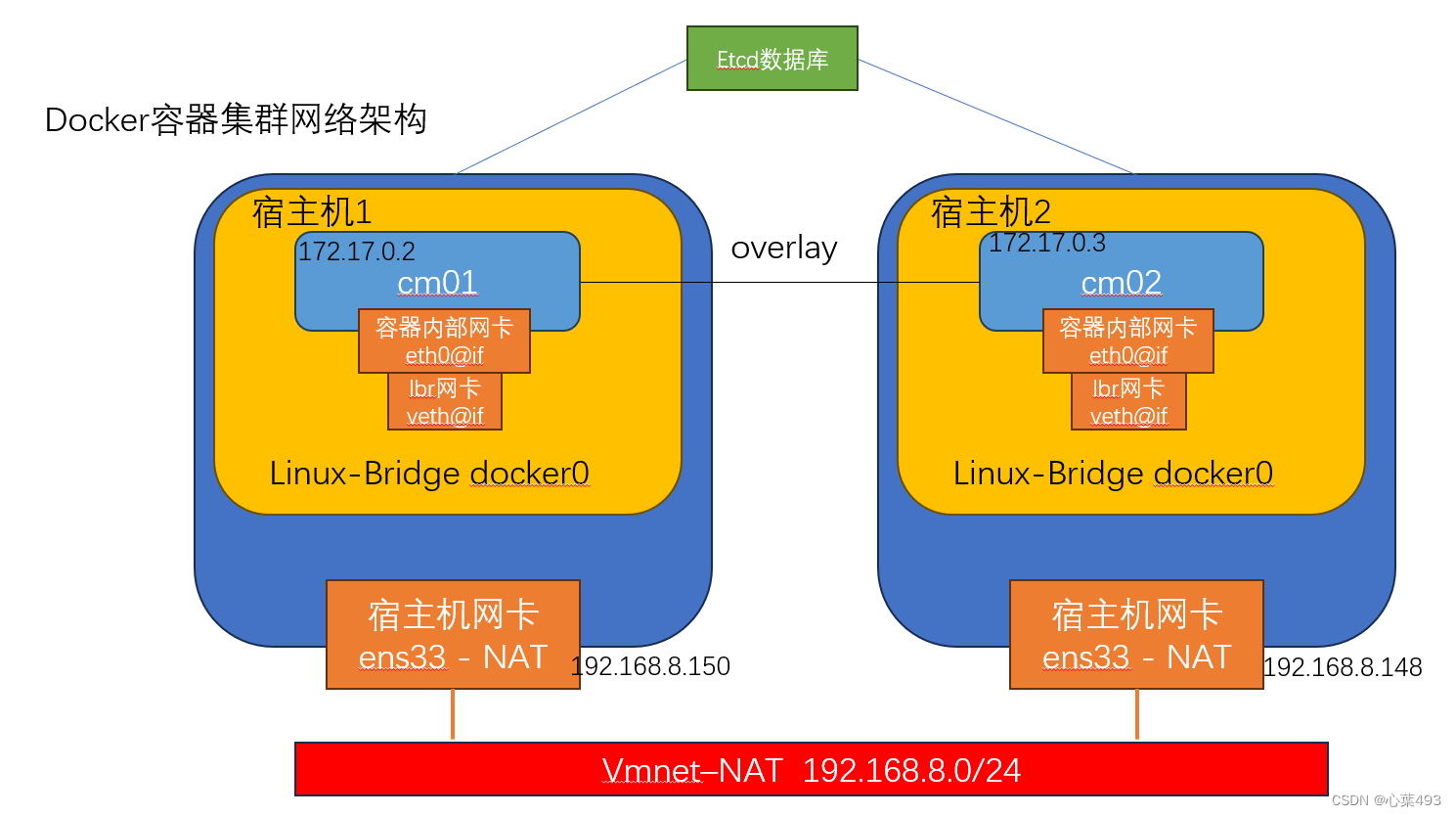
Docker网络架构介绍
本文主要介绍了Docker容器的单机网络架构与集群网络架构,辅以演示,并简单介绍了网络管理中的命令。 前文: Docker的安装与简单操作命令-CSDN博客 docker网络原理介绍 与ovs类似,docker容器采用veth-pair linux bridge (虚拟交…...

Android studio新版本aar包导入项目中配置
目录 1、so、aar导入在项目build.gradle中配置 2、新版本迁移到setting.grade配置 1、so、aar导入在项目build.gradle中配置 repositories {flatDir {dirs libs} }2、新版本迁移到setting.grade配置 flatDir {dirs libs } 如下图所示 pluginManagement {repositories {gra…...
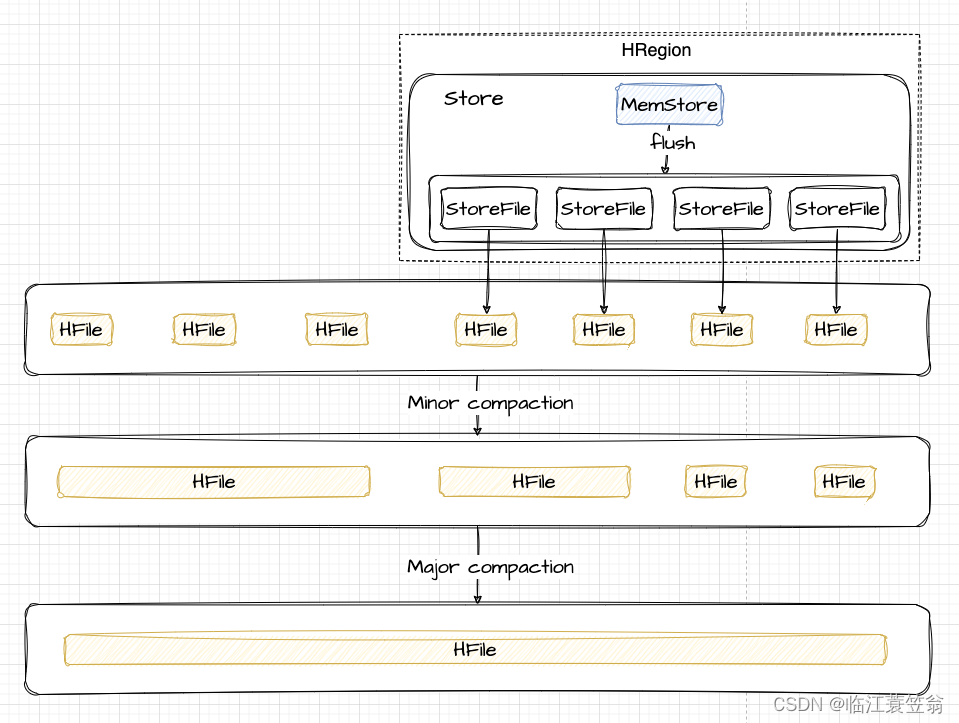
HBase-架构与设计
HBase架构与设计 一、背景二、HBase概述1.设计特点2.适用场景2.1 海量数据2.2 稀疏数据2.3 多版本数据2.4 半结构或者非结构化数据 三、数据模型1.表逻辑结构2.RowKey3.Column Family4.TimeStamp5.存储结构 四、HBase架构图1.Client2.Zookeeper3.HMaster4.HRegionServer5.HRegi…...

SpringBoot基础系列:工具类使用
断言 Assert // 要求参数 object 必须为非空(Not Null),否则抛出异常,不予放行 // 参数 message 参数用于定制异常信息。 void notNull(Object object, String message) // 要求参数必须空(Null)ÿ…...

使用 nohup java - jar 不输出日志
要在使用nohup java -jar命令时不输出日志,可以将标准输出和标准错误输出重定向到特殊设备文件/dev/null。这样做将会丢弃所有的输出。 以下是在Linux中使用nohup java -jar命令并禁止输出日志的示例: 复制代码 nohup java -jar your-application.jar …...
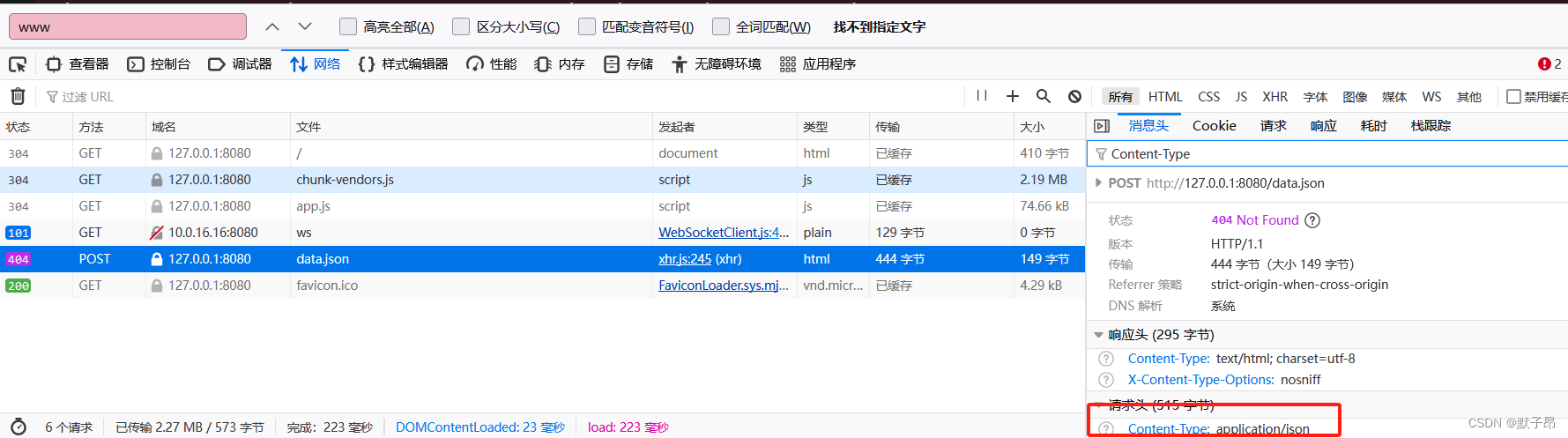
前端开发学习 (五) 生命周期函数、Ajax请求
关于vue实例的声明周期,从Vue实例创建、运行、到销毁期间,总是伴随着各种各样的事件,这些事件,统称为生命周期 (https://cn.vuejs.org/v2/guide/instance.html#实例生命周期 ) 而声明周期勾子就是生命周期…...
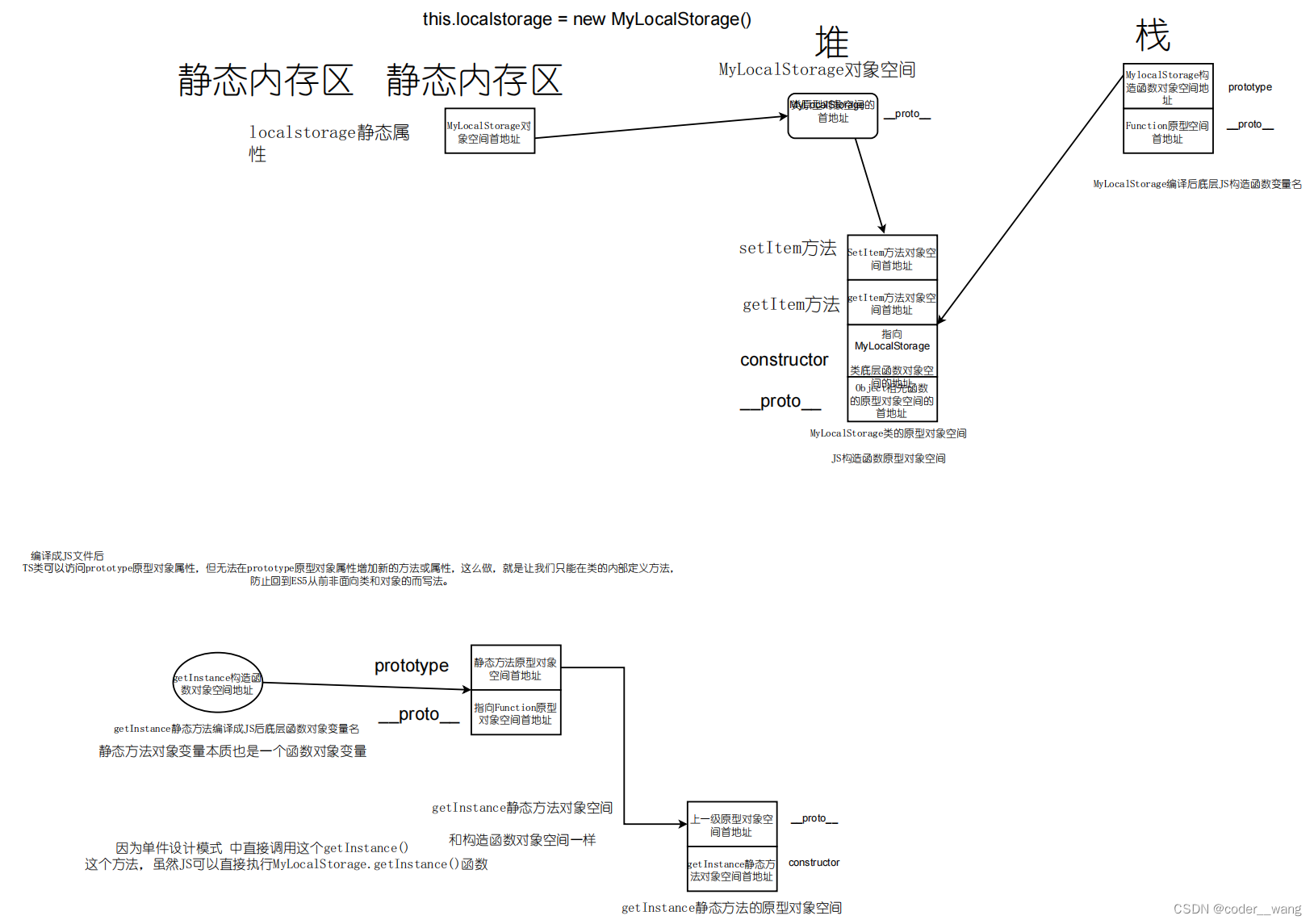
TypeScript中的单件设计模式
基本概念 (1) 了解设计模式 设计模式通俗的讲,就是一种更好的编写代码方案,打个比喻:从上海到武汉,你可以选择做飞机,做轮船,开车,骑摩托车多种方式,把出行…...

【无标题】安装环境
这里写目录标题 清华镜像加速 安装cuda11.3 PyTorch 1.10.1https://pytorch.org/get-started/previous-versions/[如果没有可以点Previous pyTorch Versions,这里面有更多的更早的版本](https://pytorch.org/get-started/locally/) 复制非空文件夹cp: -r not specif…...

一. 初识数据结构和算法
数据结构与算法是一个达到高级程序员的敲门砖。当你脱离了语言的应用层面,去思考他的设计层面时,你就依旧已经开始初识数据结构与算法了 数据结构 什么是数据结构 对于数据结构的定义官方并没有统一的解释,在各个百科以及算法的书中…...

qt 使用百度在线地图 方法1
在使用Qt和百度在线地图时,你需要从百度地图开放平台获取API密钥,并使用该密钥在Qt应用程序中集成百度地图。以下是一个简单的示例,演示了如何在Qt中使用百度在线地图: 1,首先,从百度地图开放平台获取API密…...
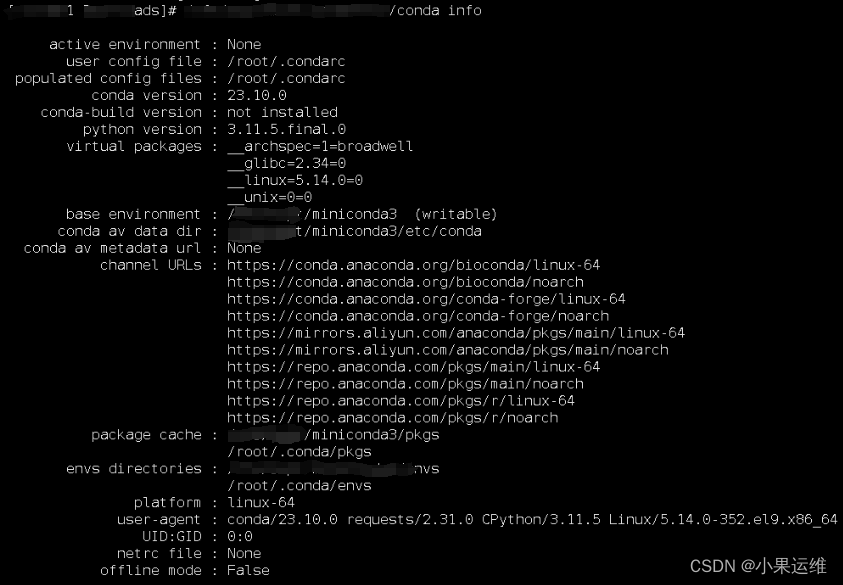
轻快小miniconda3在linux下的安装配置-centos9stream-Miniconda3 Linux 64-bit
miniconda与anaconda的区别: Miniconda 和 Anaconda 是用于管理环境和安装软件包的 Python 发行版。它们之间的主要区别在于以下几点: 1. 安装内容和大小: Anaconda: Anaconda 是一个完整的 Python 数据科学平台,包含…...
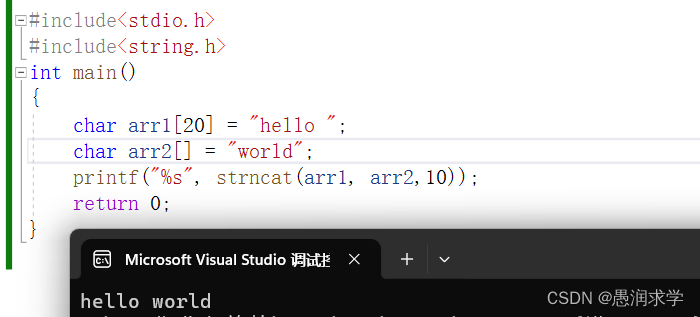
C语言——字符函数和字符串函数(一)
📝前言: 这篇文章对我最近学习的有关字符串的函数做一个总结和整理,主要讲解字符函数和字符串函数(strlen,strcpy和strncpy,strcat和strncat)的使用方法,使用场景和一些注意事项&…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...
动态规划-1035.不相交的线-力扣(LeetCode)
一、题目解析 光看题目要求和例图,感觉这题好麻烦,直线不能相交啊,每个数字只属于一条连线啊等等,但我们结合题目所给的信息和例图的内容,这不就是最长公共子序列吗?,我们把最长公共子序列连线起…...
