05. 函数式编程
目录
1、前言
2、什么是函数式编程
2.1、函数是一等公民
2.2、避免状态和可变数据
3、函数式编程的核心概念
3.1、高阶函数
3.2、Lambda(匿名函数)
3.3、递归 & 尾递归优化
3.4、functools模块
3.4.1、partial
3.4.2、reduce
3.4.3、lru_cache
3.4.4、wraps
4、函数式编程的实际应用
4.1、函数式编程风格的代码
4.2、不可变性和线程安全性
5、小结
1、前言
在《04.函数》一文中介绍了Python中的函数,以及函数的基础使用。函数是Python内建支持的一种封装,我们通过把大段代码拆成函数,通过一层一层的函数调用,就可以把复杂任务分解成简单的任务,这种分解可以称之为面向过程的程序设计。函数就是面向过程的程序设计的基本单元。而函数式编程(Functional Programming),是一种抽象程度很高的编程规范。
2、什么是函数式编程
函数式编程是一种编程范式,它将计算视为数学函数的评估,并避免改变状态和可变数据。它是一种抽象程度很高的编程范式,纯粹的函数式编程语言编写的函数没有变量,因此,任意一个函数,只要输入是确定的,输出就是确定的,这种纯函数我们称之为没有副作用。而允许使用变量的程序设计语言,由于函数内部的变量状态不确定,同样的输入,可能得到不同的输出,因此,这种函数是有副作用的。
函数式编程的一个特点就是,允许把函数本身作为参数传入另一个函数,还允许返回一个函数!在函数式编程中,函数是一等公民,允许其作为参数传递、赋值给变量,以及作为函数的返回值。
2.1、函数是一等公民
在Python中,函数是一等公民,这意味着函数可以被赋值给变量,作为参数传递给其他函数,以及作为函数的返回值。
def square(x):return x ** 2# 函数赋值给变量
f = square# 函数作为参数传递
def apply_func(func, x):return func(x)result = apply_func(f, 5) # 结果为25
2.2、避免状态和可变数据
函数式编程鼓励使用不可变数据和避免副作用。这有助于减少程序的复杂性和提高代码的可维护性。
# 不可变数据
immutable_list = (1, 2, 3)# 避免副作用
def add_to_list(element, lst):return lst + [element]original_list = [1, 2, 3]
new_list = add_to_list(4, original_list) # new_list为[1, 2, 3, 4]
3、函数式编程的核心概念
从上面的例子可以看出,编写高阶函数,就是让函数的参数能够接收别的函数。把函数作为参数传入,这样的函数称为高阶函数,函数式编程就是指这种高度抽象的编程范式。
3.1、高阶函数
高阶函数是函数式编程的基石,它们可以接受一个或多个函数作为参数,并/或返回一个新的函数。Python中内置了很多高阶函数,如map/reduce、filter、sorted等。
- map函数是一个高阶函数,将函数应用于可迭代对象的每个元素。
if __name__ == '__main__':numbers = [1, 2, 3, 4]squared = map(lambda x: x ** 2, numbers) # 结果为[1, 4, 9, 16]print(list(squared))- reduce函数用于累积可迭代对象的元素,把一个函数作用在一个序列[x1, x2, x3, ...]上,这个函数必须接收两个参数,reduce把结果继续和序列的下一个元素做累积计算。
from functools import reduceif __name__ == '__main__':numbers = [1, 2, 3, 4]total = reduce(lambda x, y: x + y, numbers) # 结果为1+2+3+4=10print(total)- filter函数用于过滤可迭代对象的元素。
if __name__ == '__main__':numbers = [1, 2, 3, 4, 5, 6]even_numbers = filter(lambda x: x % 2 == 0, numbers) # 结果为[2, 4, 6]print(list(even_numbers))3.2、Lambda(匿名函数)
Lambda函数是一种简洁的函数定义方式,通常用于临时需要一个简单函数的情况。当我们在传入函数时,有些时候,不需要显式地定义函数,直接传入匿名函数更方便。在Python中,对匿名函数提供了有限支持。就像前面filter函数中的lambda x: x % 2 == 0,该匿名函数实际上是:
def func(x):return x % 2 == 0其中关键字lambda表示匿名函数,冒号前面的x表示函数参数。匿名函数有个限制,就是只能有一个表达式,不用写return,返回值就是该表达式的结果。用匿名函数有个好处,因为函数没有名字,不必担心函数名冲突。此外,匿名函数也是一个函数对象,也可以把匿名函数赋值给一个变量,再利用变量来调用该函数。如:
if __name__ == '__main__':# 使用lambda定义匿名函数multiply = lambda x, y: x * yresult = multiply(3, 4) # 结果为12print(result)3.3、递归 & 尾递归优化
函数式编程中,递归是一种强大的技术,可以通过函数调用自身来解决问题。
# 阶乘的递归实现
def factorial(n):if n == 0 or n == 1:return 1else:return n * factorial(n - 1)
在Python并不是尾递归优化的语言,但你可以使用一些技巧来模拟尾递归优化,如使用尾递归优化装饰器。
class TailRecursive:def __init__(self, func):self.func = funcself.args = Noneself.kwargs = Nonedef __call__(self, *args, **kwargs):self.args = argsself.kwargs = kwargswhile self.args is not None:result = self.func(*self.args, **self.kwargs)if callable(result):result()else:self.args = Noneself.kwargs = Nonereturn result# 使用尾递归优化装饰器
@TailRecursive
def factorial_tail_recursive(n, acc=1):if n == 0:return accelse:return factorial_tail_recursive(n - 1, n * acc)result = factorial_tail_recursive(5) # 结果为120
3.4、functools模块
functools 是 Python 标准库中的一个模块,提供了一些与函数相关的高阶功能。它包含了一些用于函数操作的工具,其中一些特别有用于函数式编程。上面介绍reduce方法时,就已经有引入了该模块了。下面详细介绍几个常用方法,更多具体的可以详细查看API。
3.4.1、partial
该函数用于部分应用(partial application)一个函数,即固定函数的一些参数,返回一个新的函数。
from functools import partialdef power(base, exponent):return base ** exponentsquare = partial(power, exponent=2)
result = square(4) # 结果为16
3.4.2、reduce
该函数通常用于对可迭代对象的所有元素进行累积操作。
from functools import reducenumbers = [1, 2, 3, 4]
product = reduce(lambda x, y: x * y, numbers) # 结果为24
3.4.3、lru_cache
该函数用于实现缓存机制,可以缓存函数的结果,以避免重复计算。
from functools import lru_cache@lru_cache(maxsize=None)
def fibonacci(n):if n <= 1:return nreturn fibonacci(n-1) + fibonacci(n-2)
3.4.4、wraps
该函数用于在装饰器中正确处理被装饰函数的元信息,如文档字符串和函数名。
from functools import wrapsdef my_decorator(f):@wraps(f)def wrapper(*args, **kwds):print('Calling decorated function')return f(*args, **kwds)return wrapper@my_decorator
def example():"""Docstring"""print('Called example function')
这些功能使得 functools 成为编写更加灵活和可维护的代码的有用工具。在函数式编程、装饰器和缓存等方面,functools 提供了一些实用的功能。
4、函数式编程的实际应用
4.1、函数式编程风格的代码
函数式编程风格的代码通常更简洁、清晰,具有更好的可读性。
# 命令式编程
result = []
for number in numbers:result.append(number * 2)# 函数式编程
result = map(lambda x: x * 2, numbers)4.2、不可变性和线程安全性
函数式编程中的不可变性使得代码更容易在多线程环境中工作,因为不需要担心共享状态的问题。
# 命令式编程
shared_state = 0def increment_state():global shared_stateshared_state += 1# 函数式编程
immutable_state = 0def increment_state(state):return state + 15、小结
本文Python中函数式编程的基础概念、语法和实际应用。通过深入理解和应用函数式编程,你可以写出更具表达力、模块化和可维护性的代码。在实际项目中,根据需要灵活选择编程范式,将函数式编程的思想融入到你的Python代码中,发挥Python强大而灵活的特性。
相关文章:

05. 函数式编程
目录 1、前言 2、什么是函数式编程 2.1、函数是一等公民 2.2、避免状态和可变数据 3、函数式编程的核心概念 3.1、高阶函数 3.2、Lambda(匿名函数) 3.3、递归 & 尾递归优化 3.4、functools模块 3.4.1、partial 3.4.2、reduce 3.4.3、lru_…...
Linux权限(用户角色+文件权限属性)
Linux权限 文章目录 Linux权限一.文件权限1.快速掌握修改权限的方法(修改文件权限属性)2.对比权限的有无,以及具体的体现3.修改权限的第二套方法(修改用户角色)4.文件类型(Linux下一切皆文件) 二…...

短波红外相机的原理及应用场景
短波红外 (简称SWIR,通常指0.9~1.7μm波长的光线) 是一种比可见光波长更长的光。这些光不能通过“肉眼”看到,也不能用“普通相机”检测到。由于被检测物体的材料特性,一些在可见光下无法看到的特性,却能在近红外光下呈现出来&…...
【PyTorch】softmax回归
文章目录 1.理论介绍2. 代码实现2.1. 主要代码2.2. 完整代码2.3. 输出结果 3. Q&A3.1. 运行过程中出现以下警告:3.2. 定义的神经网络中的nn.Flatten()的作用是什么?3.3. num_workers有什么作用?它的值怎么确定? 1.理论介绍 背…...
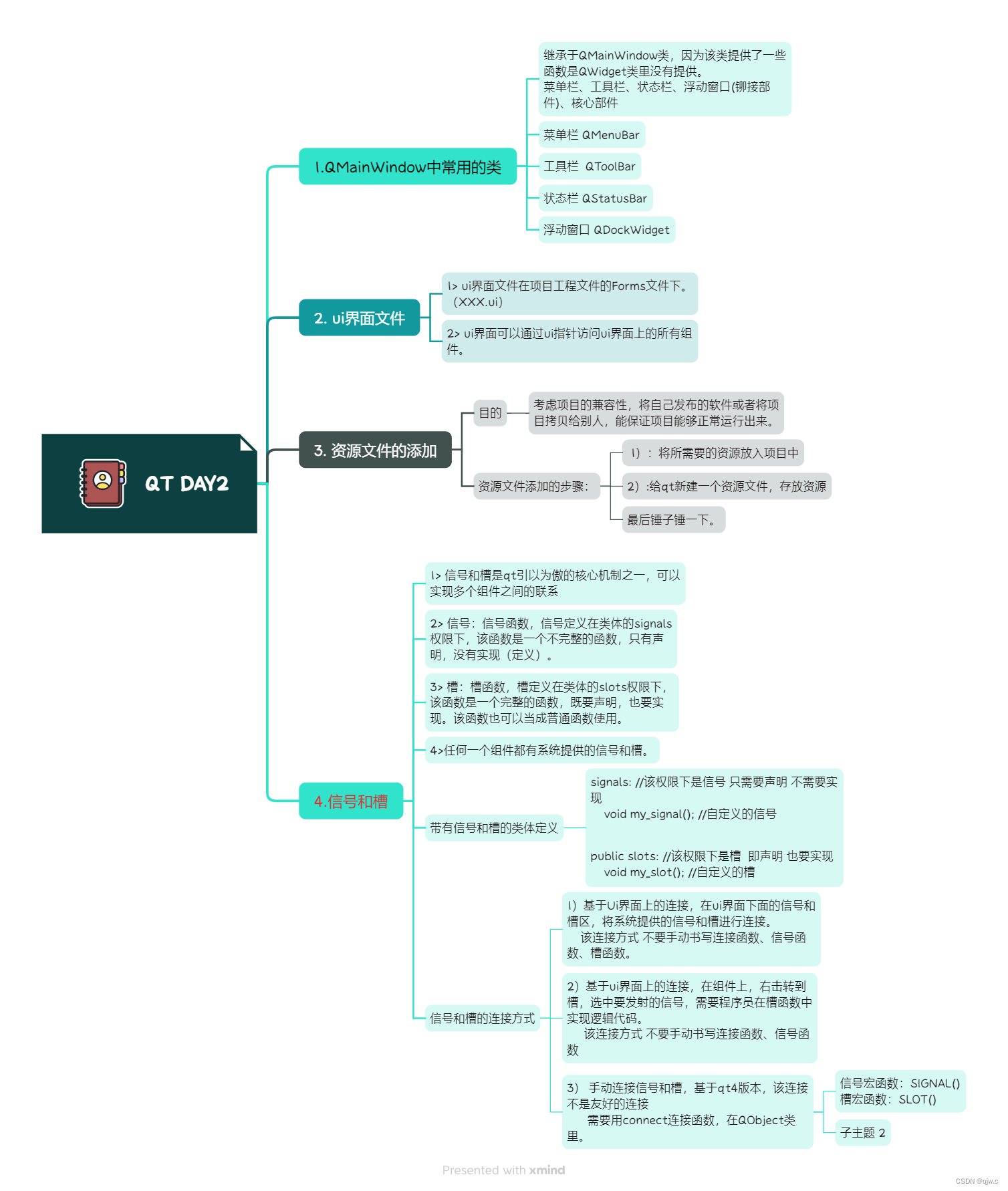
12.8 作业 C++
使用手动连接,将登录框中的取消按钮使用qt4版本的连接到自定义的槽函数中,在自定义的槽函数中调用关闭函数 将登录按钮使用qt5版本的连接到自定义的槽函数中,在槽函数中判断ui界面上输入的账号是否为"admin",密码是否为…...

10.机器人系统仿真(urdf集成gazebo、rviz)
目录 1 机器人系统仿真的必要性与本篇学习目的 1.1 机器人系统仿真的必要性 1.2 一些概念 URDF是 Unified Robot Description Format 的首字母缩写,直译为统一(标准化)机器人描述格式,可以以一种 XML 的方式描述机器人的部分结构,比如底盘…...

城市基础设施智慧路灯改造的特点
智慧城市建设稳步有序推进。作为智慧城市的基础设施,智能照明是智慧城市的重要组成部分,而叁仟智慧路灯是智慧城市理念下的新产品。随着物联网和智能控制技术的飞速发展,路灯被赋予了新的任务和角色。除了使道路照明智能化和节能化外…...
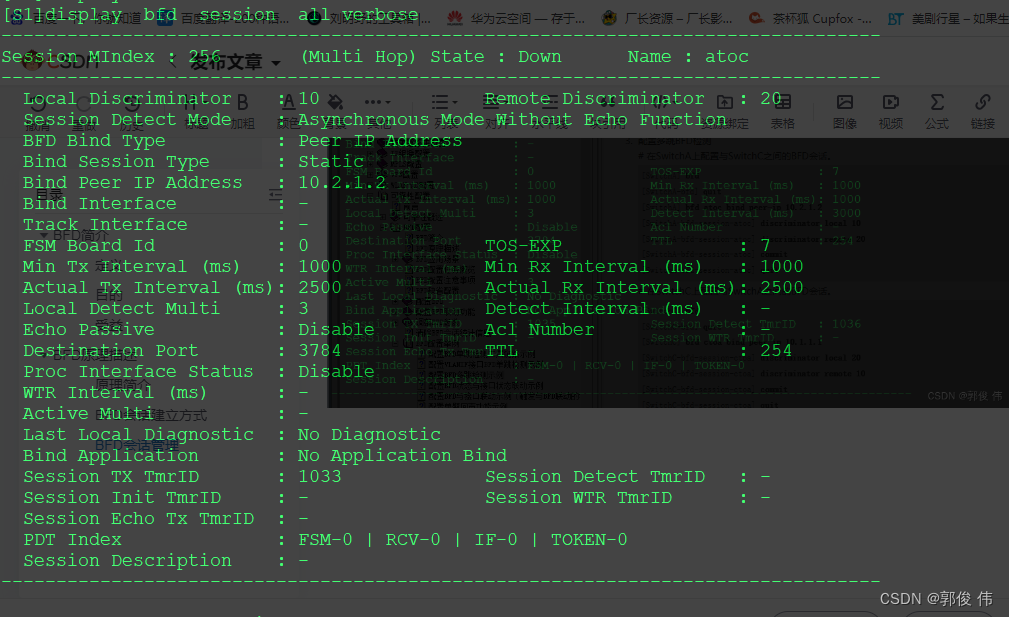
配置BFD多跳检测示例
BFD简介 定义 双向转发检测BFD(Bidirectional Forwarding Detection)是一种全网统一的检测机制,用于快速检测、监控网络中链路或者IP路由的转发连通状况。 目的 为了减小设备故障对业务的影响,提高网络的可靠性,网…...
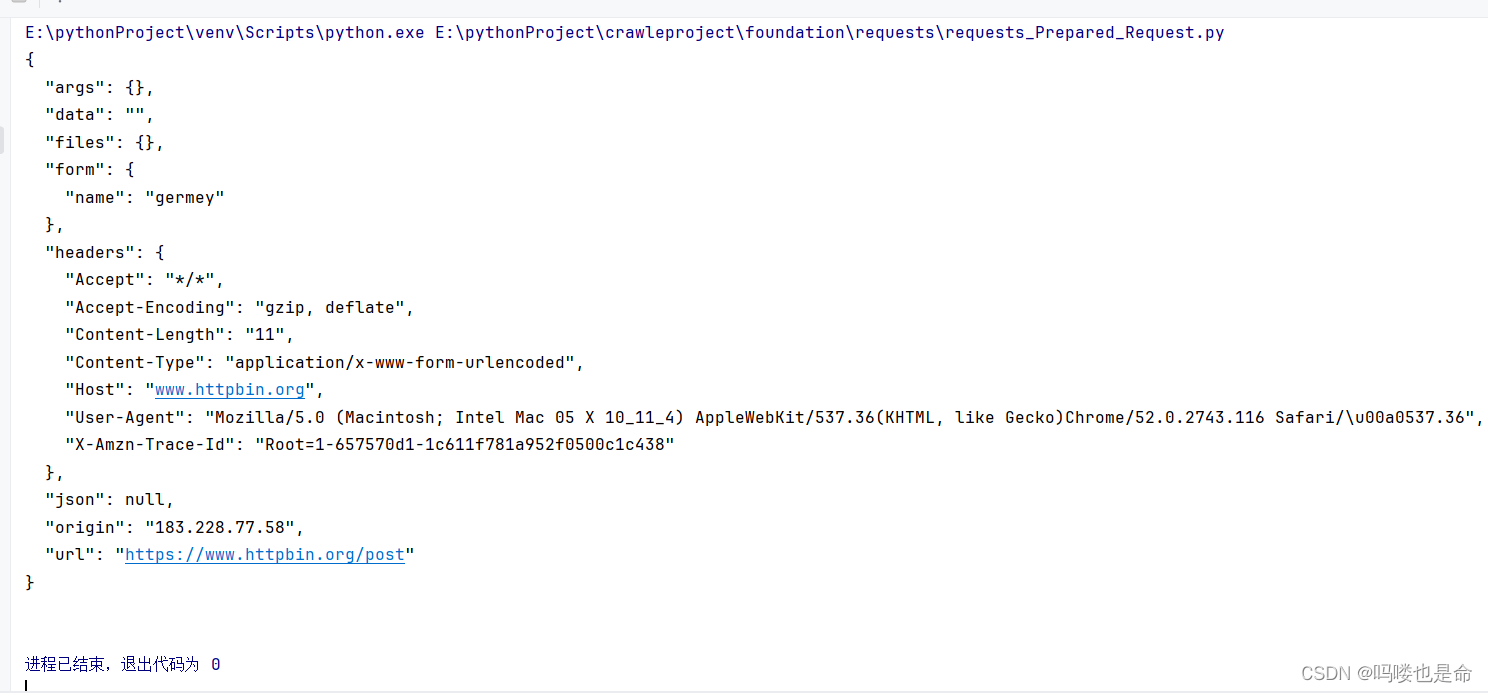
爬虫学习-基础库的使用(requests)
目录 一、安装以及实例引入 (1)requests库下载 (2)实例测试 二、GET请求 (1)基本实例 (2)抓取网页 (3)抓取二进制数据 (4)添…...
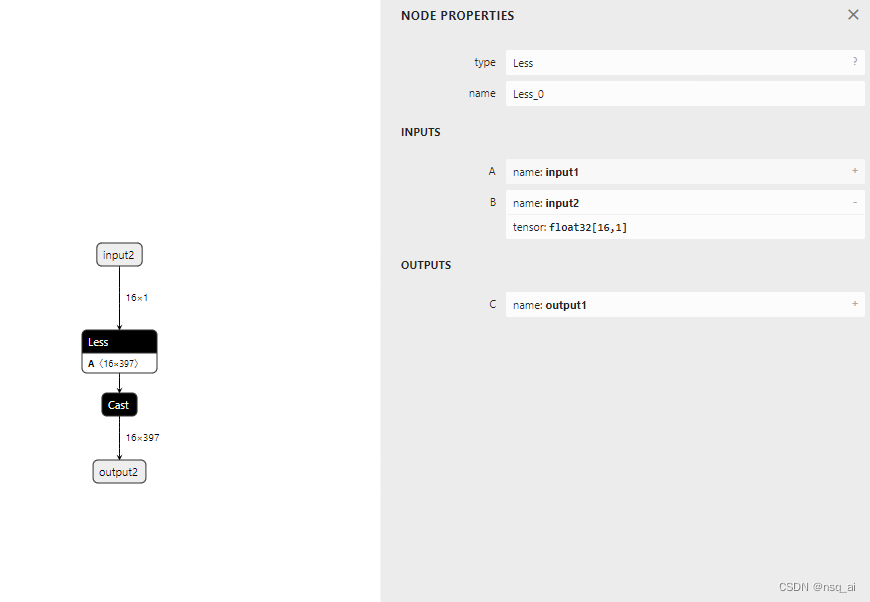
4.8 构建onnx结构模型-Less
前言 构建onnx方式通常有两种: 1、通过代码转换成onnx结构,比如pytorch —> onnx 2、通过onnx 自定义结点,图,生成onnx结构 本文主要是简单学习和使用两种不同onnx结构, 下面以 Less 结点进行分析 方式 方法一&a…...

Java调试技巧之垃圾回收机制解析
Java作为一种高级编程语言,以其跨平台、面向对象、自动内存管理等特性而广受开发者的喜爱。其中,自动内存管理是Java的一大亮点,通过垃圾回收机制实现对内存的自动分配和释放,极大地简化了开发者的工作。本文将深入探讨Java的垃圾…...
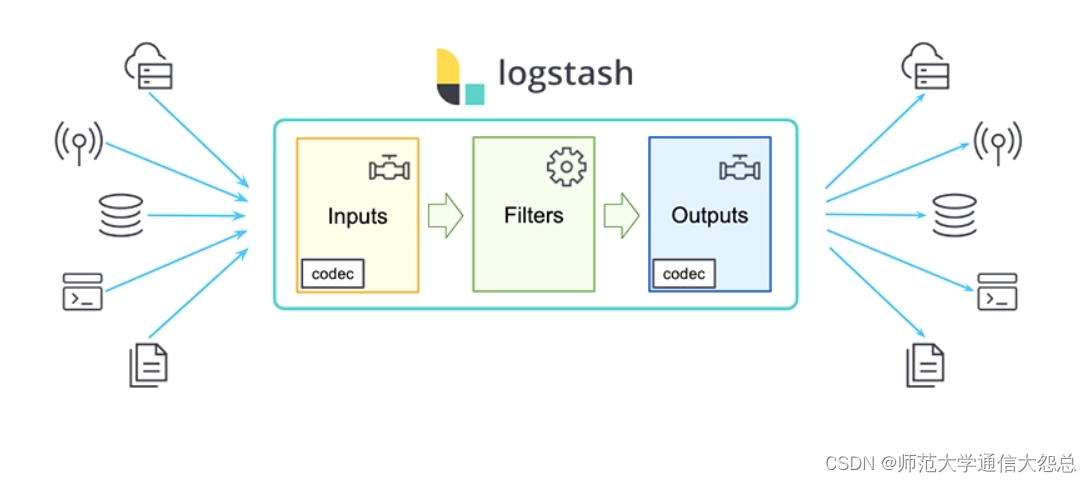
logstash插件简单介绍
logstash插件 输入插件(input) Input:输入插件。 Input plugins | Logstash Reference [8.11] | Elastic 所有输入插件都支持的配置选项 SettingInput typeRequiredDefaultDescriptionadd_fieldhashNo{}添加一个字段到一个事件codeccodecNoplain用于输入数据的…...
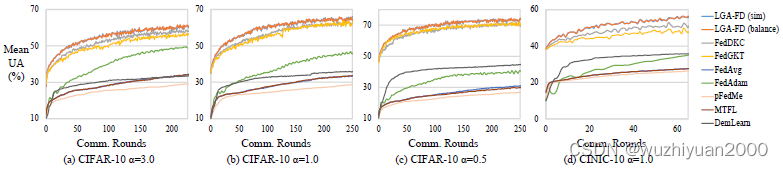
联邦多任务蒸馏助力多接入边缘计算下的个性化服务 | TPDS 2023
联邦多任务蒸馏助力多接入边缘计算下的个性化服务 | TPDS 2023 随着移动智能设备的普及和人工智能技术的发展,越来越多的分布式数据在终端被产生与收集,并以多接入边缘计算(MEC)的形式进行处理和分析。但是由于用户的行为模式与服务需求的多样,不同设备上的数据分布…...

【python爬虫】设计自己的爬虫 3. 文件数据保存封装
考虑到爬取的多媒体文件要保存到本地,因此封装了一个类来专门处理这样的问题,下面看代码: class FileStore:def __init__(self, file_path, read_file_moder,write_file_modewb):"""初始化 FileStore 实例Parameters:- file_…...
pta模拟题——7-34 刮刮彩票
“刮刮彩票”是一款网络游戏里面的一个小游戏。如图所示: 每次游戏玩家会拿到一张彩票,上面会有 9 个数字,分别为数字 1 到数字 9,数字各不重复,并以 33 的“九宫格”形式排布在彩票上。 在游戏开始时能看见一个位置上…...

【补题】 1
蓝桥杯小白赛 3.小蓝的金牌梦【算法赛】 - 蓝桥云课 (lanqiao.cn) 数组长度为质数,最大的子数组和 素数 前缀和 #include "bits/stdc.h" using namespace std; #define int long long #define N 100010 int ans[N];int s[N];vector&l…...

IP地址定位技术为网络安全建设提供全新方案
随着互联网的普及和数字化进程的加速,网络安全问题日益引人关注。网络攻击、数据泄露、欺诈行为等安全威胁层出不穷,对个人隐私、企业机密和社会稳定构成严重威胁。在这样的背景下,IP地址定位技术应运而生,为网络安全建设提供了一…...
Redis中HyperLogLog的使用
目录 前言 HyperLogLog 前言 在学习HyperLogLog之前,我们需要先学习两个概念 UV:全称Unique Visitor,也叫独立访客量,是指通过互联网访问、浏览这个网页的自然人。1天内同一个用户多次访问该网站,只记录1次。PV&am…...

新版Spring Security6.2架构 (一)
Spring Security 新版springboot 3.2已经集成Spring Security 6.2,和以前会有一些变化,本文主要针对官网的文档进行一些个人翻译和个人理解,不对地方请指正。 整体架构 Spring Security的Servlet 支持是基于Servelet过滤器,如下…...

名字的漂亮度
给出一个字符串,该字符串仅由小写字母组成,定义这个字符串的“漂亮度”是其所有字母“漂亮度”的总和。 每个字母都有一个“漂亮度”,范围在1到26之间。没有任何两个不同字母拥有相同的“漂亮度”。字母忽略大小写。给出多个字符串࿰…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...
