卷积详解和并行卷积
ps:在 TensorFlow Keras 中,构建 Sequential 模型的正确方式是将层作为列表传递,而不是作为一系列单独的参数。
model=models.Sequential([layers,layers])
而不是model=models.Sequential(layers,layers)
文章目录
- 卷积操作及其计算过程的详细解释
- 卷积的基本操作
- 1. 卷积核(Convolution Kernel)
- 卷积核如何提取特征
- 2. 卷积过程
- 卷积的数学表示
- 简单例子
- 输出尺寸的计算
- 3.卷积矩阵在深度训练中的改变过程
- 卷积核的调整过程
- 1. 初始化
- 2. 前向传播
- 3. 反向传播和卷积核的更新
- 4. 迭代过程
- 卷积核的角色
- 并行卷积结构和深度可分离卷积的详细数学解释
- 并行卷积结构:Inception 模块
- 概念
- 数学表示
- 简单例子
- 输出尺寸的计算
- 为什么不同的卷积大小产生相同的尺寸输出
- 代码
卷积操作及其计算过程的详细解释
卷积是深度学习中用于图像和信号处理的一种基本数学操作。它通过应用卷积核(或过滤器)到输入数据上,来提取重要特征。
卷积的基本操作
1. 卷积核(Convolution Kernel)
- 卷积核是一个小的矩阵(通常是2D),用于通过滤过输入数据来提取特定特征。
卷积核如何提取特征
-
边缘检测:例如,卷积核 K = [ − 1 0 1 − 1 0 1 − 1 0 1 ] K = \begin{bmatrix}-1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1\end{bmatrix} K= −1−1−1000111 被用于边缘检测。这个特定的卷积核可以突出水平方向的边缘。它通过计算左侧像素与右侧像素的差异来工作,这种差异在边缘处最大。
-
纹理和模式识别:不同的卷积核可以识别不同的纹理和模式。例如,对于识别特定方向的纹理,卷积核会有特定的方向性。
在实际应用中,通常不是手动设计这些卷积核,而是通过训练过程让神经网络自行学习最优的卷积核,以适应特定的任务和数据。
2. 卷积过程
- 将卷积核放在输入数据的左上角。
- 将卷积核的每个元素与其覆盖的输入数据元素相乘,然后将结果求和,得到输出特征图的一个元素。
- 将卷积核向右滑动一个步长(Stride),重复上述过程,直到覆盖整个输入数据。
卷积的数学表示
卷积操作可以表示为:
S ( i , j ) = ( I ∗ K ) ( i , j ) = ∑ m ∑ n I ( m , n ) K ( i − m , j − n ) S(i, j) = (I \ast K)(i, j) = \sum_m \sum_n I(m, n) K(i-m, j-n) S(i,j)=(I∗K)(i,j)=m∑n∑I(m,n)K(i−m,j−n)
其中, I I I 是输入图像, K K K 是卷积核, S S S 是输出特征图, i i i 和 j j j 表示特征图上的位置。
-
以一个 3 × 3 3 \times 3 3×3 的卷积核为例,应用于一个二维输入数据(如图像):
S ( i , j ) = ∑ m = 0 2 ∑ n = 0 2 I ( i + m , j + n ) K ( m , n ) S(i, j) = \sum_{m=0}^{2} \sum_{n=0}^{2} I(i+m, j+n) K(m, n) S(i,j)=m=0∑2n=0∑2I(i+m,j+n)K(m,n)
其中 I I I 是输入数据, K K K 是卷积核, S S S 是输出特征图, i i i 和 j j j 是特征图上的位置。
简单例子
假设输入数据是一个 4 × 4 4 \times 4 4×4 的矩阵,卷积核是一个 3 × 3 3 \times 3 3×3 的矩阵,如下所示:
输入数据 I:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
卷积核 K:
-1 0 1
-1 0 1
-1 0 1
- 将卷积核放在输入数据的左上角,计算卷积(不考虑步长和填充):
S(0, 0) = (1*-1 + 20 + 31) + (5*-1 + 60 + 71) + (9*-1 + 100 + 111)
= -1 + 0 + 3 - 5 + 0 + 7 - 9 + 0 + 11
= 7
- 将卷积核向右滑动一个步长,并重复计算。
输出尺寸的计算
输出尺寸取决于输入尺寸、卷积核尺寸、步长和填充:
Output Size = Input Size − Filter Size + 2 × Padding Stride + 1 \text{Output Size} = \frac{\text{Input Size} - \text{Filter Size} + 2 \times \text{Padding}}{\text{Stride}} + 1 Output Size=StrideInput Size−Filter Size+2×Padding+1
在不使用填充且步长为1的情况下,上述例子中的输出尺寸将是 2 × 2 2 \times 2 2×2。
3.卷积矩阵在深度训练中的改变过程
在深度学习中,卷积矩阵(或称为卷积核、过滤器)是通过训练过程逐渐调整以优化特征提取的。这个调整过程是通过反向传播算法和梯度下降方法实现的。
卷积核的调整过程
1. 初始化
- 初始化:开始训练时,卷积核的权重通常被初始化为随机小数值。
2. 前向传播
- 提取特征:在训练过程中,卷积核在前向传播阶段通过卷积操作提取输入数据的特征。
前向传播是数据通过神经网络的过程,其中的每一步如下:- 数据输入:原始数据输入网络。
- 卷积操作:数据通过卷积层,卷积核应用于数据。
- 激活函数:卷积的结果通过激活函数,如ReLU。
- 池化:可选步骤,应用池化(如最大池化)降低维度。
- 输出生成:通过全连接层生成最终输出。
3. 反向传播和卷积核的更新
卷积核的更新发生在反向传播过程中,该过程如下:
- 损失计算:计算预测输出和实际输出之间的差异(损失)。
-
损失函数衡量模型预测与实际标签之间的差距。常用的损失函数包括均方误差(MSE)和交叉熵损失。
-
假设有实际值 y y y 和预测值 y ^ \hat{y} y^,MSE 计算公式为:
MSE = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 MSE=n1i=1∑n(yi−y^i)2
其中 n n n 是样本数量。
- 梯度计算:通过反向传播算法计算损失函数相对于卷积核权重的梯度。
-
对于每个权重 W W W,损失函数的梯度计算为:
∂ Loss ∂ W = ∂ Loss ∂ y ^ × ∂ y ^ ∂ W \frac{\partial \text{Loss}}{\partial W} = \frac{\partial \text{Loss}}{\partial \hat{y}} \times \frac{\partial \hat{y}}{\partial W} ∂W∂Loss=∂y^∂Loss×∂W∂y^
- 权重更新:根据梯度和学习率更新卷积核的权重。更新公式为:
W new = W old − η × ∂ Loss ∂ W W_{\text{new}} = W_{\text{old}} - \eta \times \frac{\partial \text{Loss}}{\partial W} Wnew=Wold−η×∂W∂Loss
其中 W W W 是卷积核权重, η \eta η 是学习率, ∂ Loss ∂ W \frac{\partial \text{Loss}}{\partial W} ∂W∂Loss 是损失函数相对于 W W W 的梯度。
示例:单层神经网络
-
假设有一个单层网络,输出 y ^ = W x + b \hat{y} = Wx + b y^=Wx+b,损失函数是 MSE。
-
损失对 W W W 的梯度为:
∂ Loss ∂ W = 2 n ∑ ( y − y ^ ) × ( − x ) \frac{\partial \text{Loss}}{\partial W} = \frac{2}{n} \sum (y - \hat{y}) \times (-x) ∂W∂Loss=n2∑(y−y^)×(−x)
-
在反向传播中,这个梯度用于更新 W W W。
4. 迭代过程
- 重复迭代:这个过程在多个训练周期(epoch)中重复进行,直到模型性能达到预定的标准或者停止改进。
卷积核的角色
- 在训练过程中,卷积核逐渐学习到如何有效地提取输入数据的关键特征,这些特征对于完成特定的深度学习任务(如图像分类、物体检测等)至关重要。
并行卷积结构和深度可分离卷积的详细数学解释
并行卷积结构:Inception 模块
概念
- Inception 模块是一种在同一网络层上并行应用多种不同尺寸卷积核的结构。
- 它允许网络在单一层级上捕获多尺度特征。
数学表示
假设输入特征图为 X X X,Inception 模块中的不同分支可以表示如下:
-
1 × 1 1 \times 1 1×1 卷积分支:
Y 1 = Conv 1 × 1 ( X ) Y_1 = \text{Conv}_{1 \times 1}(X) Y1=Conv1×1(X)
这里, Conv 1 × 1 \text{Conv}_{1 \times 1} Conv1×1 表示 1 × 1 1 \times 1 1×1 卷积,用于捕获局部特征。 -
3 × 3 3 \times 3 3×3 卷积分支:
Y 2 = Conv 3 × 3 ( X ) Y_2 = \text{Conv}_{3 \times 3}(X) Y2=Conv3×3(X)
3 × 3 3 \times 3 3×3 卷积能捕获更广泛的空间特征。 -
5 × 5 5 \times 5 5×5 卷积分支:
Y 3 = Conv 5 × 5 ( X ) Y_3 = \text{Conv}_{5 \times 5}(X) Y3=Conv5×5(X)
5 × 5 5 \times 5 5×5 卷积提供了更大范围的感受野。
这些分支的输出被沿深度方向合并,生成综合特征映射 Y Y Y:
Y = [ Y 1 , Y 2 , Y 3 ] Y = [Y_1, Y_2, Y_3] Y=[Y1,Y2,Y3]
简单例子
考虑一个 224 × 224 × 3 224 \times 224 \times 3 224×224×3 的图像作为输入 X X X。Inception 模块中的 1 × 1 1 \times 1 1×1 卷积可能产生 224 × 224 × 64 224 \times 224 \times 64 224×224×64 的输出 Y 1 Y_1 Y1, 3 × 3 3 \times 3 3×3 卷积产生相同尺寸的输出 Y 2 Y_2 Y2,而 5 × 5 5 \times 5 5×5 卷积也产生相同尺寸的输出 Y 3 Y_3 Y3。合并这些输出,我们得到一个 224 × 224 × 192 224 \times 224 \times 192 224×224×192 的特征映射 Y Y Y。
输出尺寸的计算
输出特征图的尺寸取决于几个因素:
- 输入尺寸:输入图像的尺寸。
- 卷积核尺寸:卷积核的大小。
- 步长(Stride):卷积核在输入上滑动的步长。
- 填充(Padding):在输入周围添加的零的层数。
输出尺寸的计算公式为:
Output Size = Input Size − Filter Size + 2 × Padding Stride + 1 \text{Output Size} = \frac{\text{Input Size} - \text{Filter Size} + 2 \times \text{Padding}}{\text{Stride}} + 1 Output Size=StrideInput Size−Filter Size+2×Padding+1
为什么不同的卷积大小产生相同的尺寸输出
在前面的例子中, 1 × 1 1 \times 1 1×1, 3 × 3 3 \times 3 3×3 和 5 × 5 5 \times 5 5×5 的卷积产生了相同尺寸的输出,这是因为:
-
步长和填充的调整:通过调整步长和填充,可以使不同大小的卷积核产生相同尺寸的输出。通常,较大的卷积核会使用更多的填充来保持输出尺寸不变。
-
保持特征图空间分辨率:这种做法使得并行的卷积分支可以在深度方向上直接合并,因为它们具有相同的空间维度。
所以假设输入尺寸为 224 × 224 224 \times 224 224×224,卷积核尺寸分别为 1 × 1 1 \times 1 1×1, 3 × 3 3 \times 3 3×3 和 5 × 5 5 \times 5 5×5,步长为 1,并且对于 3 × 3 3 \times 3 3×3 和 5 × 5 5 \times 5 5×5 卷积使用适当的填充(分别为 1 和 2)来保持输出尺寸不变。根据上述公式,所有这些卷积操作将产生 224 × 224 224 \times 224 224×224 的输出特征图。
代码
import tensorflow as tf
from tensorflow.keras.layers import Input, Conv2D, Concatenate
from tensorflow.keras.models import Model# 定义一个函数来创建并行卷积层
def parallel_convolution(input_tensor):# 1x1 卷积conv_1x1 = Conv2D(filters=64, kernel_size=(1, 1), padding='same', activation='relu')(input_tensor)# 3x3 卷积conv_3x3 = Conv2D(filters=64, kernel_size=(3, 3), padding='same', activation='relu')(input_tensor)# 5x5 卷积conv_5x5 = Conv2D(filters=64, kernel_size=(5, 5), padding='same', activation='relu')(input_tensor)# 合并不同尺寸卷积的结果output = Concatenate()([conv_1x1, conv_3x3, conv_5x5])return output# 输入层
input_layer = Input(shape=(224, 224, 3))# 应用并行卷积层
output_layer = parallel_convolution(input_layer)# 创建模型
model = Model(inputs=input_layer, outputs=output_layer)# 查看模型概况
model.summary()
相关文章:

卷积详解和并行卷积
ps:在 TensorFlow Keras 中,构建 Sequential 模型的正确方式是将层作为列表传递,而不是作为一系列单独的参数。 modelmodels.Sequential([layers,layers]) 而不是modelmodels.Sequential(layers,layers) 文章目录 卷积…...
c#生成二维码二维码中间添加定制LoGo
🚀介绍 🍀QRCoder是一个开源的.NET库,用于生成QR码(Quick Response Code)。这个库是用C#编写的,并且可以在.NET框架的各种版本上使用,包括.NET Framework, .NET Core, Mono, Xamarin等。QRCode…...
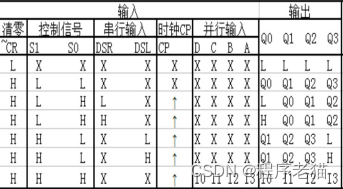
设计CPU功能的数字电路
实验目的(1)熟悉Multisim 电路仿真软件的操作界面和功能; (2)掌握逻辑电路综合设计,并采用仿真软件进行仿真。 实验内容1.试设计一个简易CPU功能的数字电路,实验至少要求采用4个74HC/HCT194作为4个存储单元(可以预先对存储单元存储数据),74HC283作为计算单元。请实现…...
在windows下编译libiconv库
libiconv是一个基于GNU协议的开源库,主要用于解决多语言编码处理转换等应用问题。在linux系统使用比较方便,但是windows下使用需要进行源码编译。这里我是使用libiconv的1.15版本源码和VS2019默认工具集配置进行编译。 首先需要用VS2019创建一个空项目,根目录为libiconv。 在…...

html,css,开发知识,调试知识
nget 方式提交 n使用 get 方式提交数据时,表单数据会附加在 URL 之后,由用户端直接发送至服务器,所以速度比 post 快,但缺点是数据长度不能太长。 npost 方式提交 n使用 post 时,表单数据是与 URL 分开发送的&#…...

Vulnerability: File Upload(Medium)--MYSQL注入
选择难度: 1.打开DVWA,并登录账户 2.选择模式,这里我们选择 文件上载的中级模式(Medium) 准备工作 1.在vsc里面写个一句话木马 2.下载BurpSuiteCommunit软件:百度搜索“burp suite官网” 下载地址www…...
短视频账号剪辑矩阵+无人直播系统源头开发
抖去推爆款视频生成器,通过短视频矩阵、无人直播,文案引流等,打造实体商家员工矩阵、用户矩阵、直播矩阵,辅助商家品牌曝光,团购转化等多功能赋能商家拓客引流。 短视频矩阵通俗来讲就是批量剪辑视频和批量发布视频&am…...

Python traceback模块:获取异常信息
异常对象提供了一个 with_traceback 用于处理异常的传播轨迹,查看异常的传播轨迹可追踪异常触发的源头,也可看到异常一路触发的轨迹。 下面示例显示了如何显示异常传播轨迹: class SelfException(Exception): passdef main():firstMethod() …...
单点登录方案调研与实现
作用 在一个系统登录后,其他系统也能共享该登录状态,无需重新登录。 演进 cookie → session → token →单点登录 Cookie 可以实现浏览器和服务器状态的记录,但Cookie会出现存储体积过大和可以在前后端修改的问题 Session 为了解决Co…...

HarmonyOS应用开发者基础认证考试(稳过)
判断题 1. Web组件对于所有的网页都可以使用zoom(factor: number)方法进行缩放。错误(False) 2. 每一个自定义组件都有自己的生命周期正确(True) 3. 每调用一次router.pushUrl()方法,默认情况下,页面栈数量会加1,页面栈支持的…...

日常开发日志
目录 1、idea开发服务启动的网页地址不显示前端样式: 2、java Date 与myibits 的空判断: 1、idea开发服务启动的网页地址不显示前端样式: idea开发时,tomcat启动的后端弹出的网页地址,呈现的网页没有样式࿰…...

【FMCW毫米波雷达设计 】 — FMCW波形
原书:FMCW Radar Design 1 引言 本章研究驱动FMCW雷达的主要波形:线性调频(LFM)波形。我们研究信号的行为及其性质。随后,本章讨论了匹配滤波理论,并研究了压缩这种波形的技术,特别是所谓的拉伸处理,它赋予FMCW雷达极…...

力扣labuladong一刷day35天
力扣labuladong一刷day35天 文章目录 力扣labuladong一刷day35天一、98. 验证二叉搜索树二、700. 二叉搜索树中的搜索三、701. 二叉搜索树中的插入操作四、450. 删除二叉搜索树中的节点 一、98. 验证二叉搜索树 题目链接:https://leetcode.cn/problems/validate-bi…...
Matlab 曲线动态绘制
axes(handles.axes1); % 选定所画坐标轴 figure也可 h1 animatedline; h1.Color b; h1.LineWidth 2; h1.LineStyle -; % 线属性设置 for i 1 : length(x)addpoints(h1,x(i),y(i)); % x/y为待绘制曲线数据drawnow;pause(0.01); % 画点间停顿 end 示例: figure…...

Spark DataFrame和Dataset使用例子
文章目录 1、基本操作1.1、创建SparkSession1.2、创建DataFrames1.3、创建Dataset操作1.4、运行sql查询1.5、创建全局临时视图1.6、创建Datasets1.7、与rdd进行互操作1.7.1、使用反射推断模式1.7.2、以编程方式指定模式 2、完整的测试例子 1、基本操作 1.1、创建SparkSession …...

CSS彩色发光液体玻璃
效果展示 CSS 知识点 animation 综合运用animation-delay 综合运用filter 的 hue-rotate 属性运用 页面整体布局 <section><div class"glass" style"--i: 1"><div class"inner"><div class"liquid"></d…...

OpenGLES:glReadPixels()获取相机GLSurfaceView预览数据并保存
Android现行的Camera API2机制可以通过onImageAvailable(ImageReader reader)回调从底层获取到Jpeg、Yuv和Raw三种格式的Image,然后通过保存Image实现拍照功能,但是却并没有Api能直接在上层直接拿到实时预览的数据。 Android Camera预览的实现是上层下发…...

小红书蒲公英平台开通后,有哪些注意的地方,以及如何进行报价?
今天来给大家聊聊当小红书账号过1000粉后,开通蒲公英需要注意的事项。 蒲公英平台是小红书APP中的一个专为内容创作者设计的平台。它为品牌和创作者提供了一个完整的服务流程,包括内容的创作、推广、互动以及转换等多个方面。 2.蒲公英平台的主要功能 &…...
持续集成交付CICD:Jenkins配置Nexus制品上传流水线
目录 一、实验 1.Jenkins配置制品上传流水线 二、问题 1.上传制品显示名称有误 一、实验 1.Jenkins配置制品上传流水线 (1) 新建流水线项目 (2)描述 (3)添加参数 (4)查看构建首页 (5&…...

C语言笔试例题_指针专练30题(附答案解析)
C语言笔试例题_指针专练30题(附答案解析) 指针一直是C语言的灵魂所在,是掌握C语言的必经之路,收集30道C语言指针题目分享给大家,测试环境位64位ubuntu18.04环境,如有错误,恳请指出,文明讨论!&am…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...
