Python高级算法——动态规划
Python中的动态规划:高级算法解析
动态规划是一种解决多阶段决策问题的数学方法,常用于优化问题。它通过将问题分解为子问题,并在解决这些子问题的基础上构建全局最优解。在本文中,我们将深入讲解Python中的动态规划,包括基本概念、状态转移方程、Memoization和Tabulation等技术,并使用代码示例演示动态规划在实际问题中的应用。
基本概念
1. 动态规划的定义
动态规划问题通常具有最优子结构和重叠子问题的特性。最优子结构意味着问题的最优解可以由子问题的最优解推导而来,而重叠子问题表示在解决问题时会多次重复计算相同的子问题。
状态转移方程
2. 动态规划的状态转移方程
动态规划问题的核心是找到递推关系,即状态转移方程。状态转移方程描述了当前状态与之前状态之间的关系,它是解决动态规划问题的关键。
Memoization
3. Memoization技术
Memoization是一种通过保存子问题的解来避免重复计算的技术。在Python中,我们通常使用字典(dictionary)来存储已经计算过的子问题的解,以提高算法的效率。
# Memoization示例
memo = {}def fib(n):if n in memo:return memo[n]if n <= 2:return 1result = fib(n - 1) + fib(n - 2)memo[n] = resultreturn result
Tabulation
4. Tabulation技术
Tabulation是一种自底向上的动态规划方法,它通过填充表格来存储子问题的解,从而构建全局最优解。
# Tabulation示例
def fib(n):if n <= 1:return ntable = [0] * (n + 1)table[1] = 1for i in range(2, n + 1):table[i] = table[i - 1] + table[i - 2]return table[n]
应用场景
动态规划广泛应用于解决各种优化问题,例如最长递增子序列、最短路径、背包问题等。它在算法设计中起到了重要的作用,能够有效解决具有最优子结构和重叠子问题性质的问题。
总结
动态规划是一种解决多阶段决策问题的强大算法,通过分解问题、建立状态转移方程,以及利用Memoization和Tabulation等技术,能够高效地求解问题。在Python中,我们可以利用递归、迭代等方式实现动态规划算法,并根据具体问题选择Memoization或Tabulation来优化算法。理解动态规划的基本概念和技术,将有助于更好地应用它解决实际问题,提高算法的效率。
相关文章:

Python高级算法——动态规划
Python中的动态规划:高级算法解析 动态规划是一种解决多阶段决策问题的数学方法,常用于优化问题。它通过将问题分解为子问题,并在解决这些子问题的基础上构建全局最优解。在本文中,我们将深入讲解Python中的动态规划,…...

MySQL在Centos7环境安装
说明: • 安装与卸载中,⽤⼾全部切换成为root,⼀旦 安装,普通⽤⼾能使⽤的 1. 卸载不要的环境 [roothcss-ecs-1036 ~]# ps ajx |grep mariadb # 先检查是否有mariadb存在 13134 14844 14843 13134 pts/0 14843 S 1005 0:00 gr…...

halcon视觉缺陷检测常用的6种方法
一、缺陷检测综述 缺陷检测是视觉需求中难度最大一类需求,主要是其稳定性和精度的保证。首先常见缺陷:凹凸、污点瑕疵、划痕、裂缝、探伤等。常用的手法有六大金刚(在halcon中的ocv和印刷检测是针对印刷行业的检测,有对应算子封装): 1.blob+特征 2.blob+差分+特征 3.光度…...

openGauss学习笔记-151 openGauss 数据库运维-备份与恢复-物理备份与恢复之gs_basebackup
文章目录 openGauss学习笔记-151 openGauss 数据库运维-备份与恢复-物理备份与恢复之gs_basebackup151.1 背景信息151.2 前提条件151.3 语法151.4 示例151.5 从备份文件恢复数据 openGauss学习笔记-151 openGauss 数据库运维-备份与恢复-物理备份与恢复之gs_basebackup 151.1 …...

报错:Uncaught ReferenceError: Cannot access ‘l‘ before initialization
在文件 .babelrc 或 babel.config.js ,webpack.config.js 下配置 .babel 或 babel.config.js "plugins": ["babel/plugin-transform-runtime" ] webpack.config.js,详见 Webpack target module.exports {target: [web, es5], }...

计算机视觉-机器学习-人工智能顶会 会议地址
计算机视觉-机器学习-人工智能顶会 会议地址 最近应该要整理中文资料的参考文献,很多会议文献都需要补全会议地点(新国标要求)。四处百度感觉也挺麻烦的,而且没有比较齐全的网站可以搜索。因此自己整理了一下计算机视觉-机器学习…...
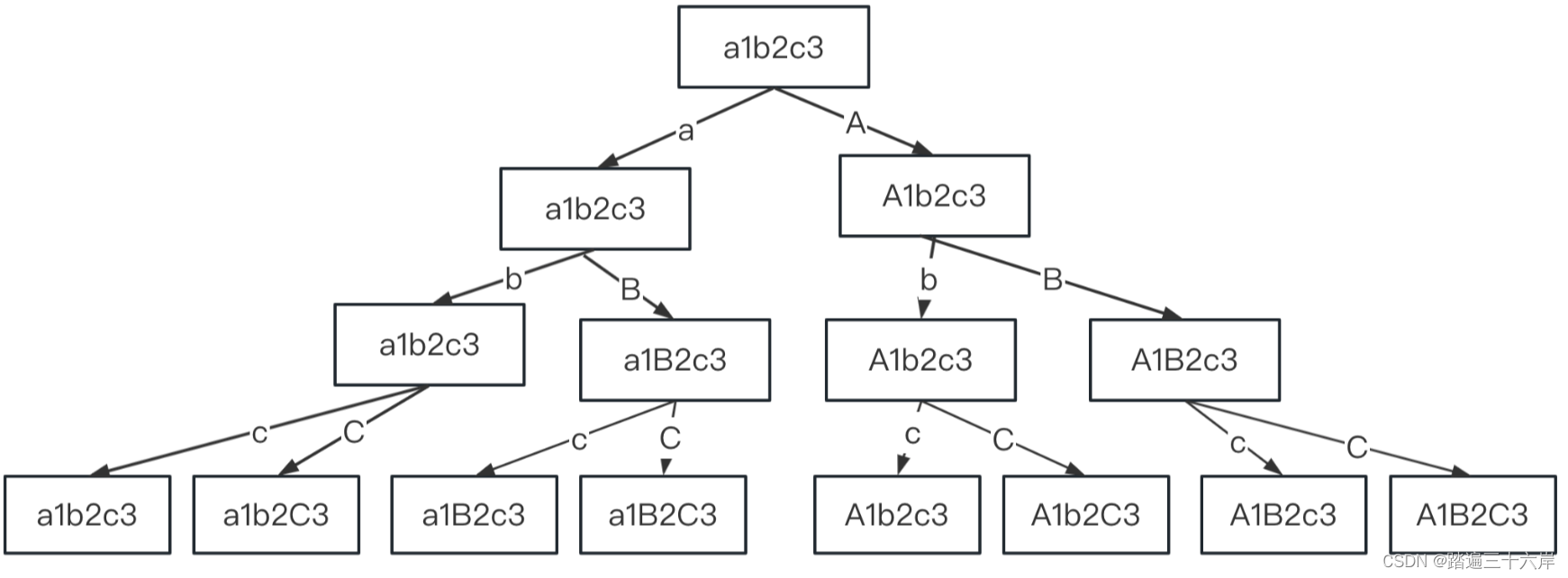
784. 字母大小写全排列
字母大小写全排列 描述 : 给定一个字符串 s ,通过将字符串 s 中的每个字母转变大小写,我们可以获得一个新的字符串。 返回 所有可能得到的字符串集合 。以 任意顺序 返回输出。 题目 : LeetCode 784.字母大小写全排列 : 784. 字母大小写全排列 分析…...
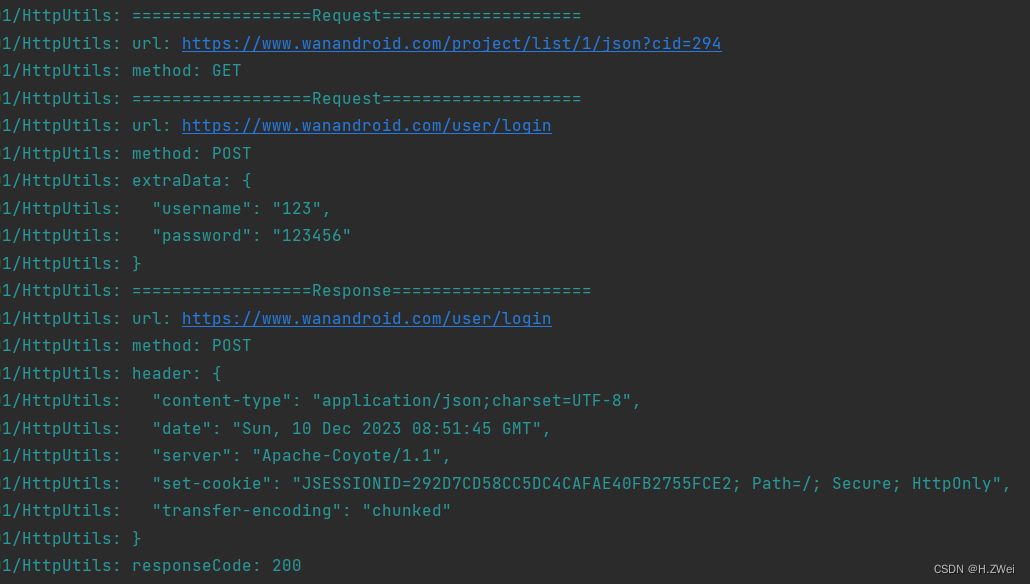
HarmonyOS鸿蒙应用开发——HTTP网络访问与封装
文章目录 基本使用封装参考 基本使用 鸿蒙应用发起HTTP请求的基本使用,如下: 导入http模块创建httpRequest对象发起http请求,并处理响应结果 第一、导入http模块: import http from ohos.net.http第二、创建httpRequest对象&a…...

vscode 编写爬虫爬取王者荣耀壁纸
网上关于爬虫大部分教程和编辑器用的都不是vscode ,此教程用到了vscode、Python、bs4、requests。 vscode配置Python安装环境可以看看这个大佬的教程 03-vscode安装和配置_哔哩哔哩_bilibili vscode配置爬虫环境可以参考这个大佬的教程【用Vscode实现简单的python…...

spring boot + uniapp 微信公众号 jsapi 支付
后端支付类 package com.ruoyi.coupon.payment;import com.google.gson.Gson; import com.ruoyi.coupon.payment.dto.PayParamJsapiDto; import com.ruoyi.coupon.payment.dto.RefundParam; import com.ruoyi.coupon.service.ICouponConfigService; import com.wechat.pay.jav…...

【数学建模】《实战数学建模:例题与讲解》第九讲-时间序列分析(含Matlab代码)
【数学建模】《实战数学建模:例题与讲解》第九讲-时间序列分析(含Matlab代码) 基本概念确定性时间序列分析方法平稳时间序列模型ARIMA模型季节性序列 习题8.11. 题目要求2.解题过程3.程序4.结果 习题8.21. 题目要求2.解题过程3.程序4.结果 习…...
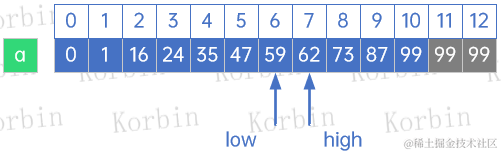
大话数据结构-查找-有序表查找
注:本文同步发布于稀土掘金。 3 有序表查找 3.1 折半查找 折半查找(Binary Search)技术,又称为二分查找,它的前提是线性表中的记录必须是关键码有序(通常从小到大有序),线性表必须…...

Qt实现二维码生成和识别
一、简介 QZxing开源库: 生成和识别条码和二维码 下载地址:https://gitcode.com/mirrors/ftylitak/qzxing/tree/master 二、编译与使用 1.下载并解压,解压之后如图所示 2.编译 打开src目录下的QZXing.pro,选择合适的编译器进行编译 最后生…...
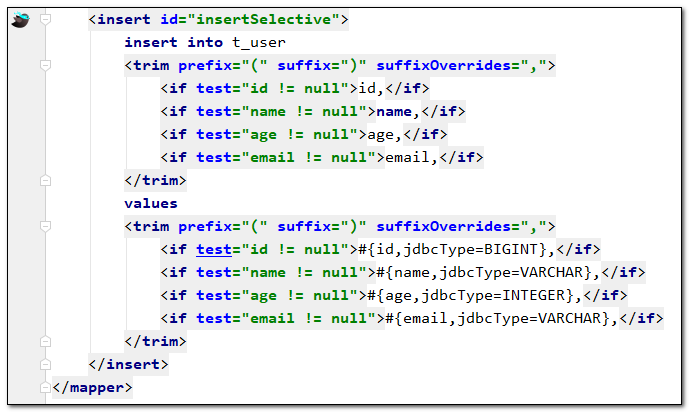
MyBatisX插件
MyBatisX插件 MyBatis-Plus为我们提供了强大的mapper和service模板,能够大大的提高开发效率。 但是在真正开发过程中,MyBatis-Plus并不能为我们解决所有问题,例如一些复杂的SQL,多表联查,我们就需要自己去编写代码和SQ…...

《C++20设计模式》学习笔记---原型模式
C20设计模式 第 4 章 原型模式4.1 对象构建4.2 普通拷贝4.3 通过拷贝构造函数进行拷贝4.4 “虚”构造函数4.5 序列化4.6 原型工厂4.7 总结4.8 代码 第 4 章 原型模式 考虑一下我们日常使用的东西,比如汽车或手机。它们并不是从零开始设计的,相反&#x…...

SpringBootAdmin设置邮件通知
如果你想要在Spring Boot Admin中配置邮件通知,可以按照以下步骤进行操作: 添加邮件通知的依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-mail</artifactId> </dep…...

深度解析IP应用场景API:提升风险控制与反欺诈能力
前言 在当今数字化时代,网络安全和用户数据保护成为企业日益关注的焦点。IP应用场景API作为一种强大的工具,不仅能够在线调用接口获取IP场景属性,而且具备识别IP真人度的能力,为企业提供了卓越的风险控制和反欺诈业务能力。本文将…...
Java连接数据库增删改查-MyBatis
准备工作: 1.创建一个springboot项目,并添加四个依赖 分别是,MyBatis的启动依赖和安装依赖,SQL的依赖,测试依赖,如下: 2.然后创建一张至少两条数据的表 (表可以用各种图形化工具创…...
在国内,现在月薪1万是什么水平?
看到网友发帖问:现在月薪1W是什么水平? 在现如今的情况下,似乎月薪过万这个标准已经成为衡量个人能力的一个标准了,尤其是现在互联网横行的时代,好像年入百万,年入千万就应该是属于大众的平均水平。 我不是…...

【Python网络爬虫入门教程1】成为“Spider Man”的第一课:HTML、Request库、Beautiful Soup库
Python 网络爬虫入门:Spider man的第一课 写在最前面背景知识介绍蛛丝发射器——Request库智能眼镜——Beautiful Soup库 第一课总结 写在最前面 有位粉丝希望学习网络爬虫的实战技巧,想尝试搭建自己的爬虫环境,从网上抓取数据。 前面有写一…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...
