辨析旅行商问题(TSP)与车辆路径问题(VRP)
目录
- 前言
- 旅行商问题 (TSP)
- 问题介绍
- 数学模型
- 符号定义
- 问题输入
- 约束条件
- 目标函数
- 问题输出
- 解的空间
- 解空间大小计算
- 解释
- 车辆路径问题 (VRP)
- 问题介绍
- TSP到VRP的过渡
- 数学模型
- 符号定义
- 问题输入
- 约束条件
- 优化目标
- 问题输出
- 解空间
- 特殊情况
- 一般情况
- TSP 与 VRP 对比
前言
计划是通过本文的撰写,捋清楚TSP和VRP的本质不同。(什么是本质❔)
| 对比 | TSP(旅行商问题) | VRP(车辆路径问题) |
|---|---|---|
| 描述 | 给定一个城市列表以及每对城市之间的距离,访问每个城市一次并返回出发城市的最短路线是什么 | 车队需要向给定的一组客户家中取货,需要遍历的最佳路线集是什么? |
| 输入 | 城市数量,距离矩阵 | 城市数量,距离矩阵,任务量,卡车容量 |
| 约束 | 每个城市仅访问一次 | 每个城市仅访问一次,满足容量要求 |
| 目标 | 最小化总旅行距离 | 最小化总旅行距离 |
| 输出 | 一个旅行商访问城市的顺序 | 多个车辆的行驶路线 |
| 空间 | 城市序列: ( n − 1 ) ! (n-1)! (n−1)! | 城市序列加上车辆任务分配: n ! < S < P ( n , m ) k n! < S < P(n,m)^k n!<S<P(n,m)k |
以 n = 13 , m = 5 , k = 3 n=13,m=5,k=3 n=13,m=5,k=3为例,对比解空间:
- TSP解空间: ( n − 1 ) ! = ( 13 − 1 ) ! = 12 ! = 4.79 × 1 0 8 (n-1)! = (13-1)! = 12!=4.79 × 10^8 (n−1)!=(13−1)!=12!=4.79×108
- VRP解空间:
- 下限: n ! = 13 ! = 12 ! = 6.23 × 1 0 9 n! = 13! = 12!= 6.23 × 10^9 n!=13!=12!=6.23×109
- 上限: P ( n , m ) k = P ( 15 , 5 ) 3 = 3.68 × 1 0 15 P(n,m)^k=P(15,5)^3= 3.68 × 10^{15} P(n,m)k=P(15,5)3=3.68×1015
旅行商问题 (TSP)
问题介绍
旅行商问题(英语:Travelling salesman problem, TSP)在1930年被首次提出,是优化领域研究最深入的问题之一。问题的表述是:“给定一个城市列表以及每对城市之间的距离,访问每个城市一次并返回出发城市的最短路线是什么?”
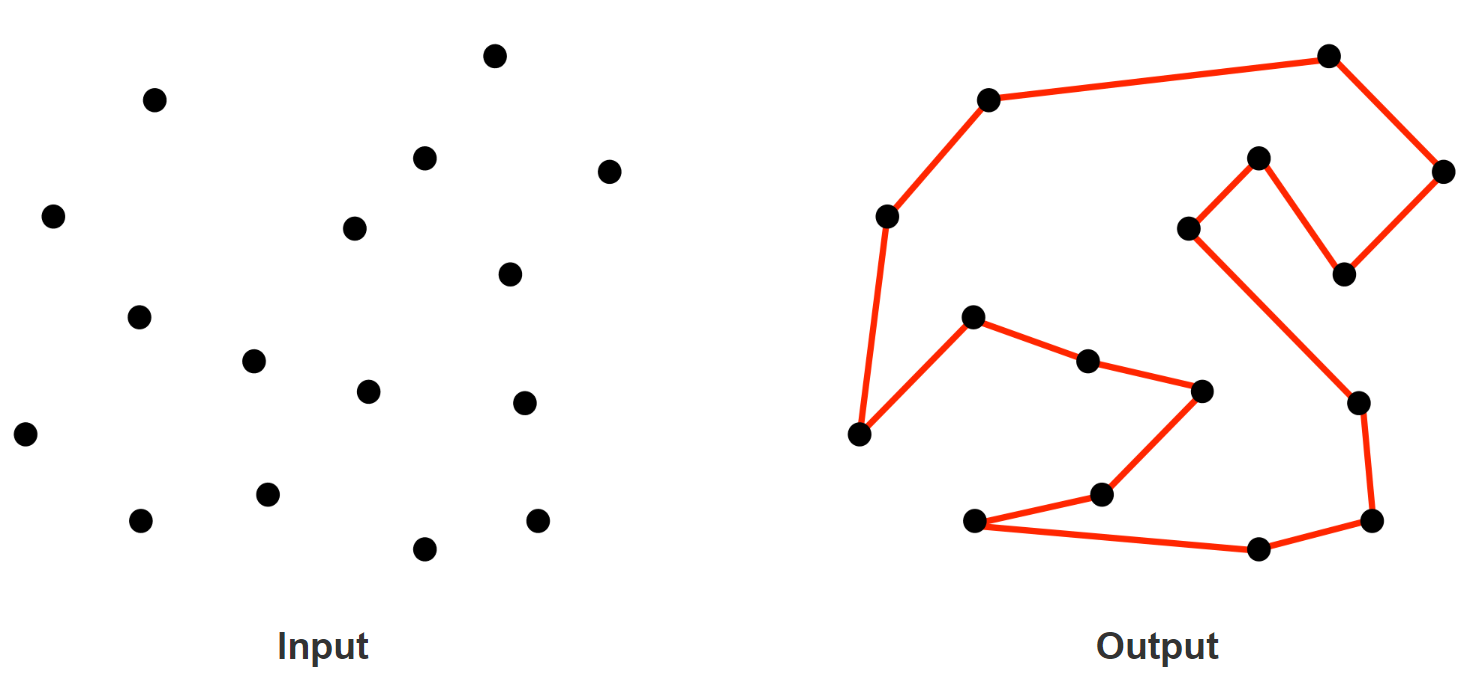
图片来源:algorist.com
数学模型
符号定义
- n n n: 城市的数量。
- c i j c_{ij} cij: 从城市 i i i 到城市 j j j 的距离或成本。
- x i j x_{ij} xij: 决策变量。如果旅行商从城市 i i i 直接前往城市 j j j,则为 1,否则为 0。
问题输入
- 城市数量: n n n
- 距离矩阵: c i j c_{ij} cij,表示从城市 i i i 到城市 j j j 的距离或成本(对所有 i , j = 1 , 2 , . . . , n i, j = 1, 2, ..., n i,j=1,2,...,n 且 i ≠ j i \neq j i=j)。
约束条件
每个城市只访问一次:
∑ j = 1 , j ≠ i n x i j = 1 ∀ i = 1 , 2 , … , n \sum_{j=1, j \neq i}^{n} x_{ij} = 1 \quad \forall i = 1, 2, \ldots, n j=1,j=i∑nxij=1∀i=1,2,…,n
∑ i = 1 , i ≠ j n x i j = 1 ∀ j = 1 , 2 , … , n \sum_{i=1, i \neq j}^{n} x_{ij} = 1 \quad \forall j = 1, 2, \ldots, n i=1,i=j∑nxij=1∀j=1,2,…,n
$$
\sum_{j=1, j \neq i}^{n} x_{ij} = 1 \quad \forall i = 1, 2, \ldots, n
$$
$$
\sum_{i=1, i \neq j}^{n} x_{ij} = 1 \quad \forall j = 1, 2, \ldots, n
$$
目标函数
最小化总旅行距离或成本:
min ∑ i = 1 n ∑ j = 1 , j ≠ i n c i j x i j \min \sum_{i=1}^{n}\sum_{j=1, j \neq i}^{n} c_{ij} x_{ij} mini=1∑nj=1,j=i∑ncijxij
$$
\min \sum_{i=1}^{n}\sum_{j=1, j \neq i}^{n} c_{ij} x_{ij}
$$
问题输出
- 访问城市的顺序。
解的空间
旅行商问题的解空间是指所有可能的路径组合数量。
解空间大小计算
- 对于 n n n 个城市的 TSP,旅行商从一个城市出发,并有 ( n − 1 ) (n - 1) (n−1) 个城市可以选择作为第一站。
- 在访问了第一个城市后,剩下 ( n − 2 ) (n - 2) (n−2) 个城市可以选择作为下一站,以此类推。
- 最后,旅行商将从最后一个未访问的城市返回起始城市。
因此,TSP 的解空间大小为所有可能路径的数量,计算公式为:
( n − 1 ) ! (n - 1)! (n−1)!
其中, ( n − 1 ) ! (n - 1)! (n−1)! 表示 ( n − 1 ) (n - 1) (n−1) 的阶乘,即 1 × 2 × 3 × … × ( n − 2 ) × ( n − 1 ) 1 \times 2 \times 3 \times \ldots \times (n - 2) \times (n - 1) 1×2×3×…×(n−2)×(n−1)。
解释
旅行商可以从任何城市开始,但是不同的起点并不会影响各城市在解中的相对顺序。每个路径都可以通过循环移位变换为从特定城市(比如第一个城市)开始的路径,所以实际上只需考虑从一个固定城市出发的路径。
车辆路径问题 (VRP)
问题介绍
车辆路径问题(英语:Vehicle Routing Problem,VRP)在1959年被首次提出,是TSP的泛化形式,包含TSP问题。问题描述:车队需要向给定的一组客户家中取货或是送货,需要遍历的最佳路线集是什么?
值得一提的是,在1959年被提出时,论文名称是’The truck dispatching problem’,并没有使用Vehicle Routing Problem的表述。在随后十多年的相关研究中,也一直没有直接使用VRP这一名词的论文。直到Christofides, N.的论文’The vehicle routing problem’于1976年发表后,后续研究普遍采用了VRP的表述。
TSP到VRP的过渡
我们把TSP问题或一个场景表述为一辆空载的卡车从车库或是车场(出发城市)出发需要到多位客户的家中(其它城市)取货物,待取完所有货物后需要返回车库。这里有一个潜在的假定,不管所有客户家中的货物累加和究竟有多大,这一辆卡车总能全部纳入到自己的车厢中并继续正常行驶。也就是,车辆的运输能力 C C C 大于等于所有的货物量:
C ≥ ∑ i q i C \ge \sum\limits_i {{q_i}} C≥i∑qi
其中 q i q_i qi 表述第 i i i 个客户家中的货物量。
但是,当面临一辆卡车完不成所有的任务量时,也就是:
C < ∑ i q i C < \sum\limits_i {{q_i}} C<i∑qi
就需要多辆车去完成,或者是一辆车多次往返。
按照论文The truck dispatching problem. Management science 6, 80–91 (1959)里面的介绍,把该条件描述为:
C ≪ ∑ i q i C \ll \sum\limits_i {{q_i}} C≪i∑qi
并且,文章提出假定一辆车最多只能访问 m m m 个点,只有当 m m m 比较大时,有研究意义,否则的话,求解比较容易,如下:
If m m m is small, optimal sets of m m m points may often be determined by inspection of a map which contains the points and the arcs connecting them. One would look for “clusters of points” and determine by trial and error the order in which they should be traversed, taking care that no loop crosses itself. However, when clusters are not present in sufficient numbers or when m m m is large, this procedure becomes inapplicable. In this case near-best solutions may be obtained by the algorithm in this paper.
如果 m m m 很小,最优的 m m m 个点的集合通常可以通过检查包含这些点和连接它们的弧的地图来确定。人们会寻找"点的簇集",并通过试验和错误来确定它们应该按照什么顺序遍历,确保没有回路交叉。然而,当簇集数量不足或者 m m m 很大时,这种方法就不适用了。在这种情况下,可以通过本文中的算法获得近似最优解。
数学模型
符号定义
- n n n: 任务点的数量。
- P i P_i Pi: 第 i i i 个任务点的位置,( i = 1 , 2 , … , n i=1,2,\ldots,n i=1,2,…,n)。
- [ D ] = [ d i j ] [D]=[d_{ij}] [D]=[dij]: 任务点间的距离邻接矩阵,( i , j = 0 , 1 , … , n i,j=0,1,\ldots,n i,j=0,1,…,n)。
- ( Q ) = ( q i ) (Q) = (q_i) (Q)=(qi): 各任务点的任务量,( i = 1 , 2 , … , n i=1,2,\ldots,n i=1,2,…,n)。
- C C C: 卡车的容量,满足 C > max ( q i ) C > \max(q_i) C>max(qi)。
- x i j x_{ij} xij: 决策变量。如果任务点 P i P_i Pi 和 P j P_j Pj 被同一辆车辆访问,则 x i j = x j i = 1 x_{ij} = x_{ji} = 1 xij=xji=1;如果不被同一辆车辆访问,则 x i j = x j i = 0 x_{ij} = x_{ji} = 0 xij=xji=0;对于所有 i i i, x i i = 0 x_{ii} = 0 xii=0。
问题输入
- 给定 n n n 个任务点的位置 P i P_i Pi。
- 给定任务点间的距离邻接矩阵 [ D ] [D] [D]。
- 给定任务点的任务量 ( Q ) (Q) (Q)。
- 给定卡车的容量 $C。
约束条件
- 车辆的起点和终点均是车库 P 0 P_0 P0。
- 每个任务点 P i P_i Pi 除了与车库 P 0 P_0 P0 外,最多与另一个任务点 P j P_j Pj 被同一个车辆访问一次。对于所有 i = 1 , 2 , … , n i = 1, 2, \ldots, n i=1,2,…,n,有 ∑ j = 0 n x i j = 1 \sum_{j = 0}^{n} x_{ij} = 1 ∑j=0nxij=1。
- 每辆车辆在任何时候的载荷不得超过其容量 C C C。对于车辆在访问任务点 P i P_i Pi 时的载荷量,满足以下条件:
∑ i = 1 n q i x i j ≤ C ∀ j = 1 , 2 , … , n \sum_{i=1}^{n} q_i x_{ij} \le C \quad \forall j = 1, 2, \ldots, n i=1∑nqixij≤C∀j=1,2,…,n
其中, q i q_i qi 表示任务点 P i P_i Pi 的任务量, x i j x_{ij} xij 表示车辆是否访问了任务点 P i P_i Pi。
$$\sum_{i=1}^{n} q_i x_{ij} \le C \quad \forall j = 1, 2, \ldots, n$$
优化目标
最小化总行驶距离 D D D:
min D = ∑ i , j = 0 n d i j x i j \min D = \sum_{i,j=0}^n d_{ij} x_{ij} minD=i,j=0∑ndijxij
$$\min D = \sum_{i,j=0}^n d_{ij} x_{ij}$$
问题输出
- 各车辆的行驶路线。
解空间
在车辆路径问题(VRP)中,我们考虑除起点和终点外的所有车辆行驶路线。这些路线可以排列成一个由 n n n 个点组成的一维序列 S S S,拥有 n ! n! n! 种可能性。
特殊情况
假设 n n n 是 m m m 的整数倍,且每辆车必须经过 m m m 个点才能返回车库。此时,序列 S S S 只需平均分配给各车辆,解空间仍为 n ! n! n! 种。
一般情况
如果每辆车经过的点数在 1 到 m m m 之间,解空间的计算变得复杂。
目前尚没有发现计算精确解空间大小的文献, AI 也无法给出确切数字,下面是一个粗略的估算方法。
- 单辆车的最大访问点数为 m m m,可能的访问序列数量为排列数 P ( n , m ) P(n,m) P(n,m)。
- 对于 k k k 辆车,考虑所有可能的序列组合。
- 考虑到车辆间访问点的重叠,实际解空间小于 P ( n , m ) k P(n,m)^k P(n,m)k。
因此,解空间的上限估算为 P ( n , m ) k P(n,m)^k P(n,m)k。
TSP 与 VRP 对比
| 对比条目 | TSP(旅行商问题) | VRP(车辆路径问题) |
|---|---|---|
| 问题描述 | 给定一个城市列表以及每对城市之间的距离,访问每个城市一次并返回出发城市的最短路线是什么 | 车队需要向给定的一组客户家中取货,需要遍历的最佳路线集是什么? |
| 问题输入 | 城市数量,距离矩阵 | 城市数量,距离矩阵,任务量,卡车容量 |
| 约束条件 | 每个城市仅访问一次 | 每个城市仅访问一次,满足容量要求 |
| 优化目标 | 最小化总旅行距离 | 最小化总旅行距离 |
| 问题输出 | 一个旅行商访问城市的顺序 | 多个车辆的行驶路线 |
| 求解空间 | 城市序列: ( n − 1 ) ! (n-1)! (n−1)! | 城市序列加上车辆任务分配: n ! < S < P ( n , m ) k n! < S < P(n,m)^k n!<S<P(n,m)k |
以n=13,m=5,k=3为例
- TSP解空间: ( n − 1 ) ! = ( 13 − 1 ) ! = 12 ! = 4.79 × 1 0 8 (n-1)! = (13-1)! = 12!=4.79 × 10^8 (n−1)!=(13−1)!=12!=4.79×108
- VRP解空间:
- 下限: n ! = 13 ! = 12 ! = 6.23 × 1 0 9 n! = 13! = 12!= 6.23 × 10^9 n!=13!=12!=6.23×109
- 上限: P ( n , m ) k = P ( 15 , 5 ) 3 = 3.68 × 1 0 15 P(n,m)^k=P(15,5)^3= 3.68 × 10^{15} P(n,m)k=P(15,5)3=3.68×1015
- 理解本质区别了吗?
- 啥是本质,还是迷迷糊糊的😶🌫️,似乎是还差点,又似乎是还差许多💫。下雪了,开心👻

- 啥是本质,还是迷迷糊糊的😶🌫️,似乎是还差点,又似乎是还差许多💫。下雪了,开心👻
相关文章:

辨析旅行商问题(TSP)与车辆路径问题(VRP)
目录 前言旅行商问题 (TSP)问题介绍数学模型符号定义问题输入约束条件目标函数问题输出 解的空间解空间大小计算解释 车辆路径问题 (VRP)问题介绍TSP到VRP的过渡数学模型符号定义问题输入约束条件优化目标问题输出 解空间特殊情况一般情况 TSP 与 VRP 对比 前言 计划是通过本文…...

2024年JAVA招聘行情如何?
大家都在说Java求职不好找,是真的吗?我们来看看数据。 数据支持:根据TIOBE 5月份的编程语言排行榜,Java仍然是前三名之一。这意味着,Java在开发领域仍然占据重要地位。 而在中国的IT市场中,Java仍然是主要…...
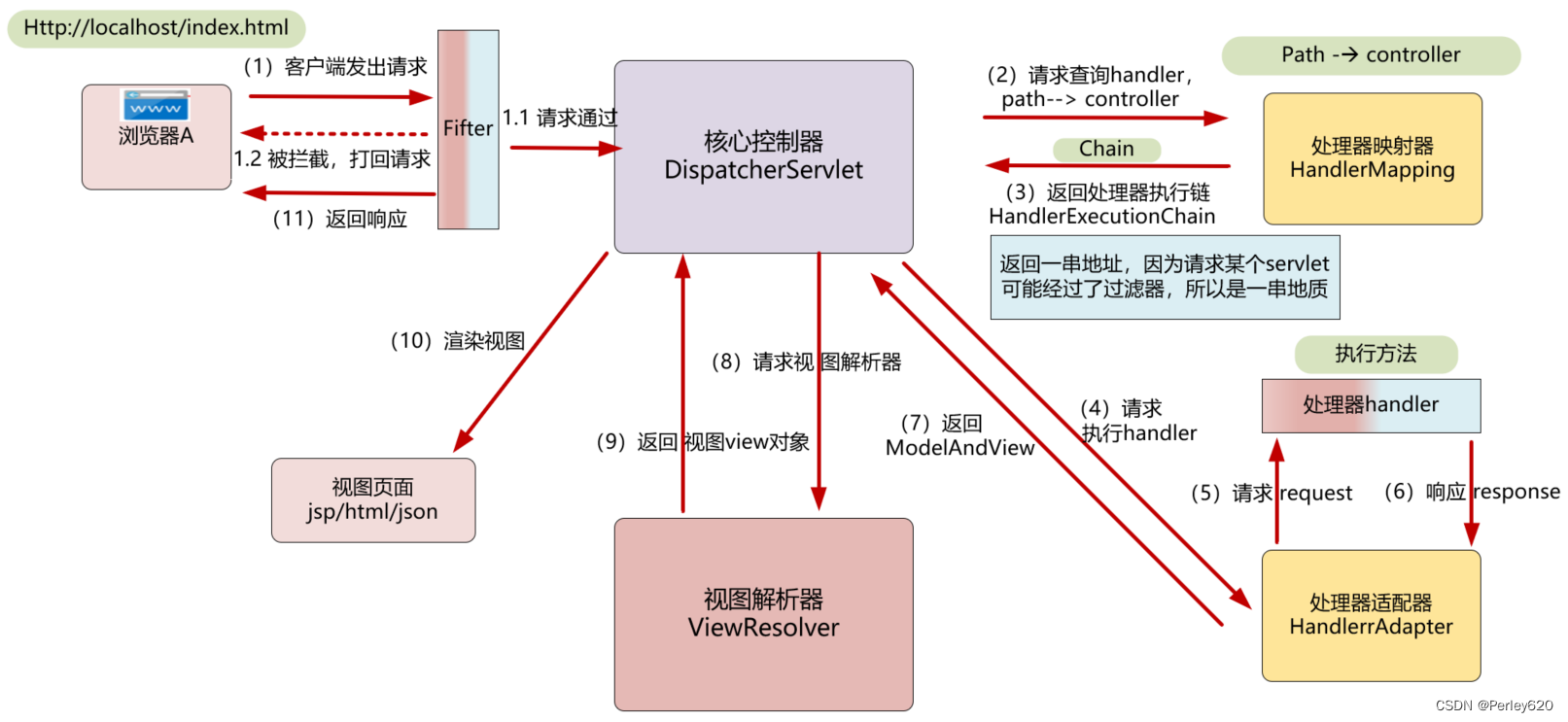
【合集】SpringBoot——Spring,SpringBoot,SpringCloud相关的博客文章合集
前言 本篇博客是spring相关的博客文章合集,内容涵盖Spring,SpringBoot,SpringCloud相关的知识,包括了基础的内容,比如核心容器,springMVC,Data Access;也包括Spring进阶的相关知识&…...

yolov5 获取漏检图片脚本
yolov5 获取漏检图片脚本 获取样本分数在0.05到0.38直接的样本。 # YOLOv5 by Ultralytics, GPL-3.0 licenseimport argparse import json import os import sys import time from pathlib import Pathimport cv2 import numpy as np import torch import torch.backends.cud…...
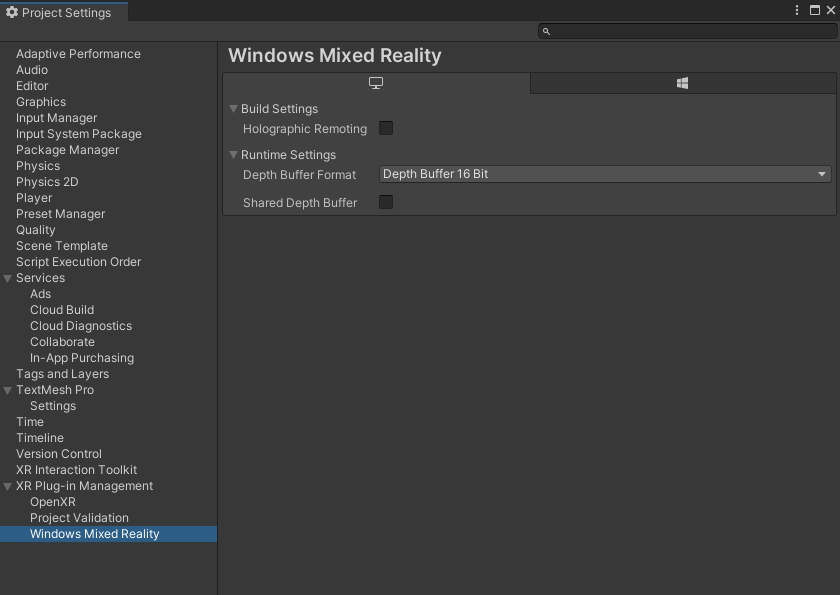
Unity之OpenXR+XR Interaction Toolkit接入微软VR设备Windows Mixed Reality
前言 Windows Mixed Reality 是 Microsoft 用于增强和虚拟现实体验的VR设备,如下图所示: 在国内,它的使用率很低,一把都是国外使用,所以适配起来是相当费劲。 这台VR设备只能用于串流Windows,启动后,会自动连接Window的Mixed Reality程序,然后打开微软的增强现实门户…...

【小聆送书第二期】人工智能时代AIGC重塑教育
🌈个人主页:聆风吟 🔥系列专栏:网络奇遇记、数据结构 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋正文📝活动参与规则 参与活动方式文末详见。 📋正文 AI正迅猛地…...

中国移动公网IP申请过程
一、动机 由于从事互联网行业10年,一直从事移动端(前端)开发工作,未曾深入了解过后端技术,以至于工作10年也不算进入互联网的门。 所以准备在自己家用设备上搭建各种场景的服务器(云服务对个人来说成本偏…...
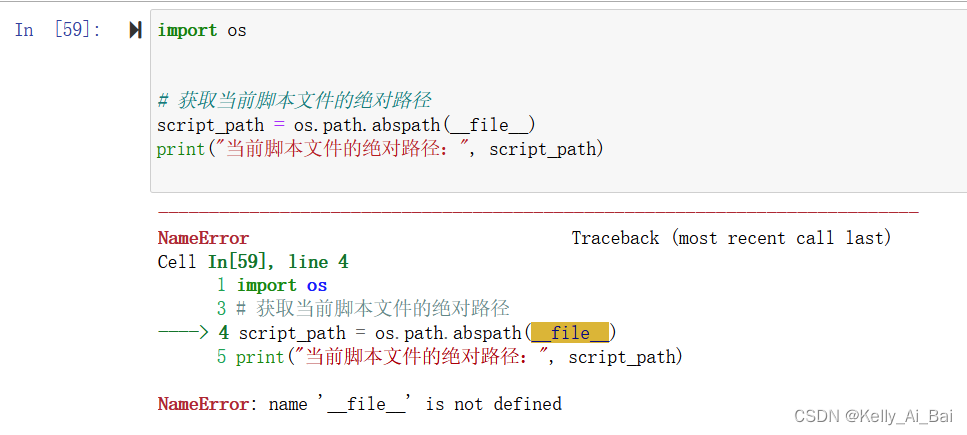
动态获取绝对路径
在Python中,可以使用 os模块 来获取当前工作目录的路径,并使用 os.path.join()函数 将相对路径与当前工作目录结合起来,形成一个动态获取的绝对路径 以下是一个简单的例子: import os# 获取当前工作目录的路径 current_director…...

pytorch中的归一化:BatchNorm、LayerNorm 和 GroupNorm
1 归一化概述 训练深度神经网络是一项具有挑战性的任务。 多年来,研究人员提出了不同的方法来加速和稳定学习过程。 归一化是一种被证明在这方面非常有效的技术。 1.1 为什么要归一化 数据的归一化操作是数据处理的一项基础性工作,在一些实际问题中&am…...
--顺序消息)
RocketMq源码分析(九)--顺序消息
文章目录 一、顺序消息二、顺序消息消费过程1、消息队列负载2、消息拉取3、消息消费4、消息进度存储 三、总结 一、顺序消息 RocketMq在同一个队列中可以保证消息被顺序消费,所以如果要做到消息顺序消费,可以将消费主题(topic)设置…...
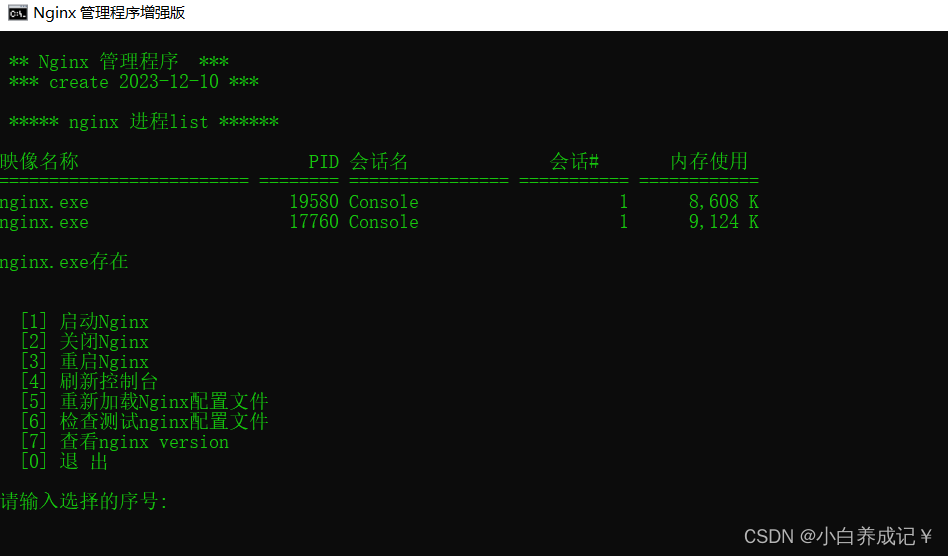
Windows下nginx的启动,重启,关闭等功能bat脚本
echo off rem 提供Windows下nginx的启动,重启,关闭功能echo begincls ::ngxin 所在的盘符 set NGINX_PATHG:::nginx 所在目录 set NGINX_DIRG:\projects\nginx-1.24.0\ color 0a TITLE Nginx 管理程序增强版CLSecho. echo. ** Nginx 管理程序 *** echo.…...
之间的区别)
Python 字典:dic = {} 和 dic = defaultdict(list)之间的区别
d defaultdict(list) 和 d {} 在Python中代表了两种不同类型的字典初始化方式,它们之间有几个关键的区别: 1、类型 d defaultdict(list):这里使用的是 collections 模块中的 defaultdict 类。它是一个字典的子类,提供了一个默…...
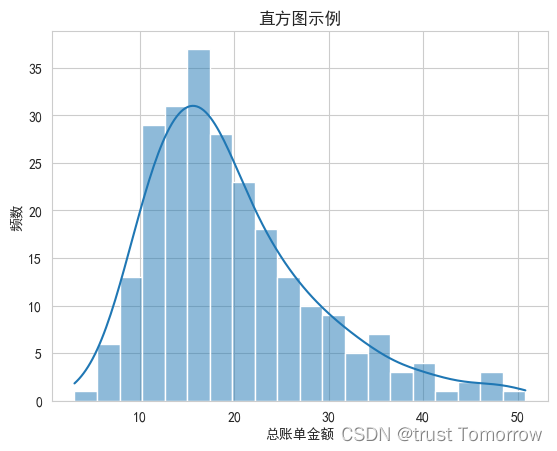
绘图 Seaborn 10个示例
绘图 Seaborn 是什么安装使用显示中文及负号散点图箱线图小提琴图堆叠柱状图分面绘图分类散点图热力图成对关系图线图直方图 是什么 Seaborn 是一个Python数据可视化库,它基于Matplotlib。Seaborn提供了高级的绘图接口,可以用来绘制各种统计图形…...
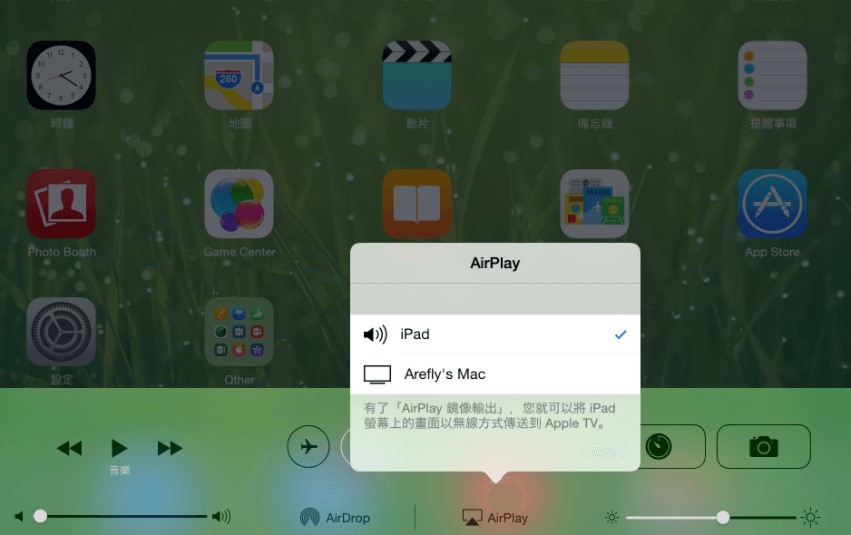
airserver mac 7.27官方破解版2024最新安装激活图文教程
airserver mac 7.27官方破解版是一款好用的airplay投屏工具,可以轻松将ios荧幕镜像(airplay)至mac上,在mac平台上实现视频、音频、幻灯片等文件资源的接收及投放演示操作,解决iphone或ipad的屏幕录像问题,满…...
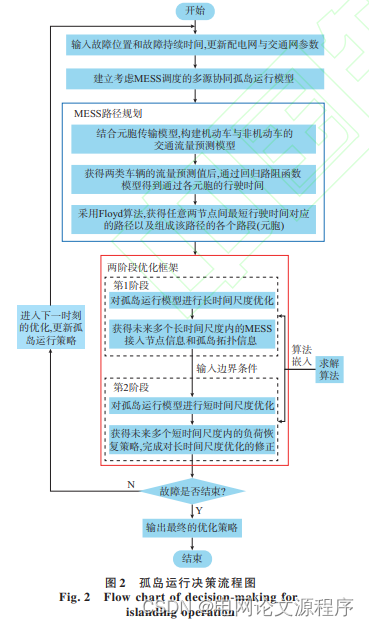
文章解读与仿真程序复现思路——电力系统自动化EI\CSCD\北大核心《考虑移动式储能调度的配电网灾后多源协同孤岛运行策略》
这篇文章的标题表明研究的主题是在配电网发生灾害后,采用一种策略来实现多源协同孤岛运行,并在这个过程中特别考虑了移动式储能的调度。 让我们逐步解读标题的关键词: 考虑移动式储能调度: 文章关注的焦点之一是移动式储能系统的…...

Spring Boot 优雅地处理重复请求
前 言 对于一些用户请求,在某些情况下是可能重复发送的,如果是查询类操作并无大碍,但其中有些是涉及写入操作的,一旦重复了,可能会导致很严重的后果,例如交易的接口如果重复请求可能会重复下单。 重复的场…...

TailwindCSS 多主题色配置
TailwindCSS 多主题色配置 现在大多数网站都支持主题色变换,比如切换深色模式。那么我们该如何进行主题色配置呢? tailwind dark tailwind 包含一个 dark变体,当启用深色模式时,可以为网站设置不同样式 <div class"bg-whi…...
Vue3:表格单元格内容由:图标+具体内容 构成
一、背景 在Vue3项目中,想让单元格的内容是由 :图标具体内容组成的,类似以下效果: 二、图标 Element-Plus 可以在Element-Plus里面找是否有符合需求的图标iconfont 如果Element-Plus里面没有符合需求的,也可以在这…...

【项目日记(一)】高并发内存池项目介绍
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:项目日记-高并发内存池⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习C 🔝🔝 项目日记 1. 前言2. 什么是高并发内存池…...

4-Docker命令之docker commit
1.docker commit介绍 docker commit命令是用于根据docker容器的改变创建一个新的docker镜像 2.docker commit用法 docker commit [参数] container [repository[:tag]] [rootcentos79 ~]# docker commit --helpUsage: docker commit [OPTIONS] CONTAINER [REPOSITORY[:TAG…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
