java面试-Dubbo和zookeeper运行原理
远离八股文，面试大白话，通俗且易懂
看完后试着用自己的话复述出来。有问题请指出，有需要帮助理解的或者遇到的真实面试题不知道怎么总结的也请评论中写出来，大家一起解决。
java面试题汇总-目录-持续更新中
分布式注册中心和服务调用的原理大多如此：
1.Dubbo和zookeeper运行原理
1.首先搞懂zookeeper和dubbo框架中的角色
Provider: 暴露服务的服务提供方【服务提供方】
Consumer: 调用远程服务的服务消费方【服务消费方】
Registry: 服务注册与发现的注册中心。
Monitor: 统计服务的调用次调和调用时间的监控中心。
Container: 服务运行容器
2. 运行原理逻辑
1.首先容器负责启动、加载、运行服务提供者
2.服务提供者在启动时，向注册中心注册自己提供的服务接口
3.服务消费者在启动时，向注册中心订阅自己需要的服务接口
4.注册中心将消费者所需的接口地址列表返回给消费者，如果有变更，则基于长连接将变更数据更新给消费者。
5.消费者从提供者列表中国，基于负载均衡算法，选择一台提供者进行调用，如果失败会重试另外一台（提供者列表是指zookeeper分布式集群部署）
6.服务消费者和提供者，会在本地内存中累计调用次数和调用时间，然后定时每分钟会发送到监控中心
相关文章：
java面试-Dubbo和zookeeper运行原理
远离八股文，面试大白话，通俗且易懂 看完后试着用自己的话复述出来。有问题请指出，有需要帮助理解的或者遇到的真实面试题不知道怎么总结的也请评论中写出来，大家一起解决。 java面试题汇总-目录-持续更新中 分布式注册中心和服务调…...
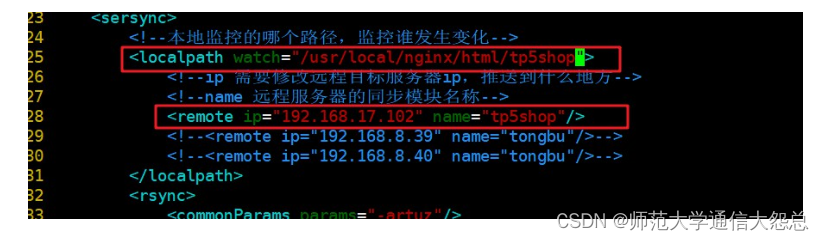
Rsync+Sersync
服务器相关参数 源服务器 192.168.17.101 目标服务器（同步到的服务器） 192.168.17.103 ##目标服务器配置 ###1、配置rsync服务 1、安装rsync yum -y install rsync 2、配置rsync vim /etc/rsyncd.conf 配置文件内容 uid root gid root use c…...
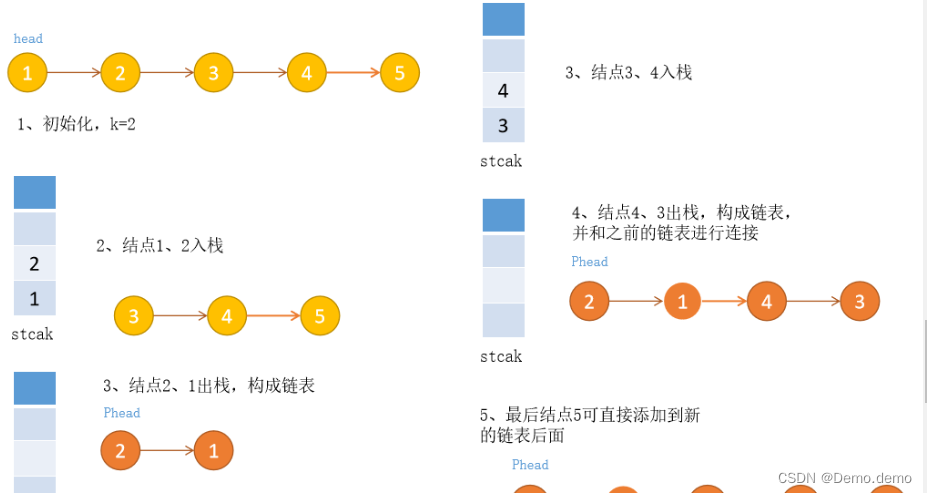
Leetcode刷题笔记题解（C++）：25. K 个一组翻转链表
思路：利用栈的特性，K个节点压入栈中依次弹出组成新的链表，不够K个节点则保持不变 /*** struct ListNode {* int val;* struct ListNode *next;* ListNode(int x) : val(x), next(nullptr) {}* };*/ #include <stack> class Solution { …...
从线性回归到神经网络
目录 一、线性回归关键思想 1、线性模型 2、基础优化算法 二、线性回归的从零开始实现 1、生成数据集 2、读取数据集 3、初始化模型参数 4、定义模型 5、定义损失函数 6、定义优化算法 7、训练 三、线性回归的简洁实现 1、生成数据集 2、读取数据集 3、定义模型…...
LANDSAT_7/02/T1/RAW的Landsat7_C2_RAW类数据集
Landsat7_C2_RAW是指Landsat 7卫星的数据集，采用的是Collection 2级别的数据处理方法，对应的是Tier 1级别的原始数据（RAW）。该数据集包括了Landsat 7卫星从1999年4月15日开始的所有数据，共涵盖了全球范围内的陆地和海洋…...
绕过360给目标机器添加账户
CS BOF是什么？ Beacon 对象文件 (BOF) 是一个已编译的 C 程序，按照约定编写，允许其在 Beacon 进程内执行并使用内部 Beacon API。BOF 是一种通过新的利用后功能快速扩展 Beacon 代理的方法。 BOF 的占地面积较小。它们在 Beacon 进程内部运…...
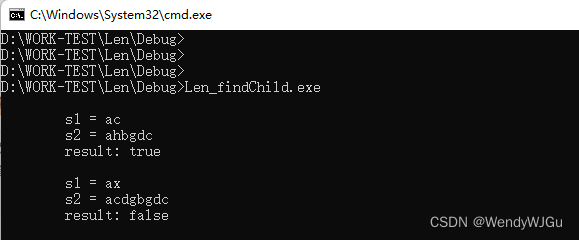
C/C++ 题目：给定字符串s1和s2，判断s1是否是s2的子序列
判断子序列一个字符串是否是另一个字符串的子序列 解释：字符串的一个子序列是原始字符串删除一些（也可以不删除）字符，不改变剩余字符相对位置形成的新字符串。 如，"ace"是"abcde"的一个子序…...
Nginx的stream配置
一、stream模块概要。 stream模块一般用于tcp/UDP数据流的代理和负载均衡，可以通过stream模块代理转发TCP消息。 ngx_stream_core_module模块由1.9.0版提供。 默认情况下，没有构建此模块。 -必须使用-with stream配置参数启用。 也就是说，必…...
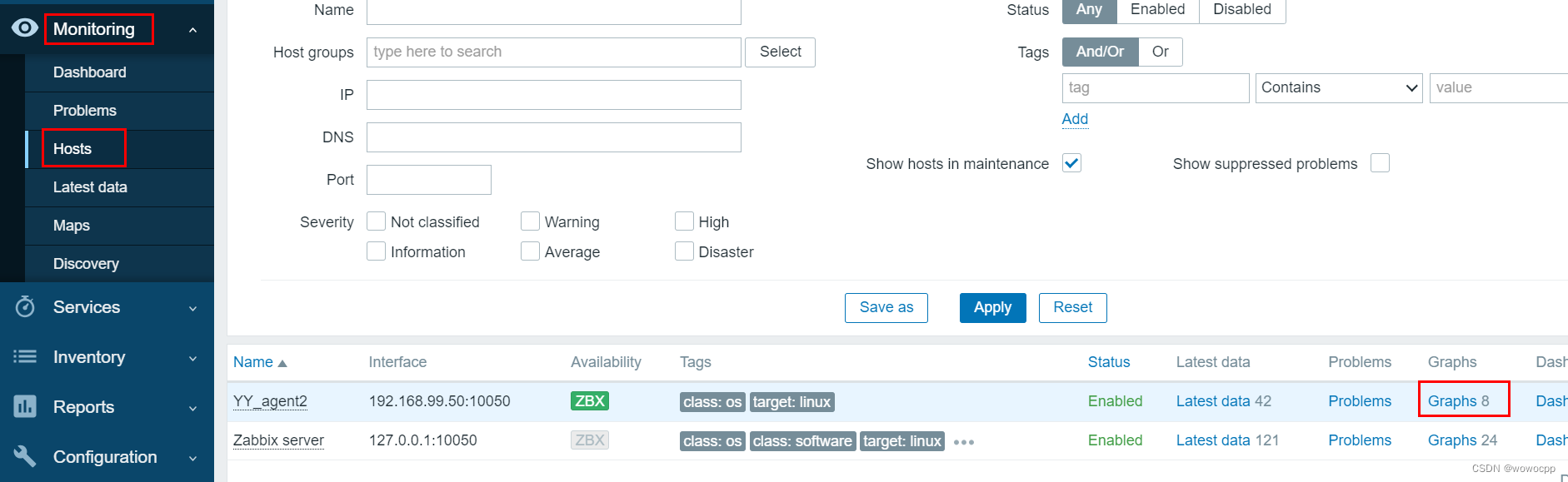
ubuntu 20.04 server 安装 zabbix
ubuntu 20.04 server 安装 zabbix 参考文档 zabbix没用过，用过prometheus， 因为现在很多应用都支持直接接入prometheus监控， 而且大部分语言都都有sdk支持， 可以直接接入自己的业务数据监控。 https://www.zabbix.com/cn/downlo…...
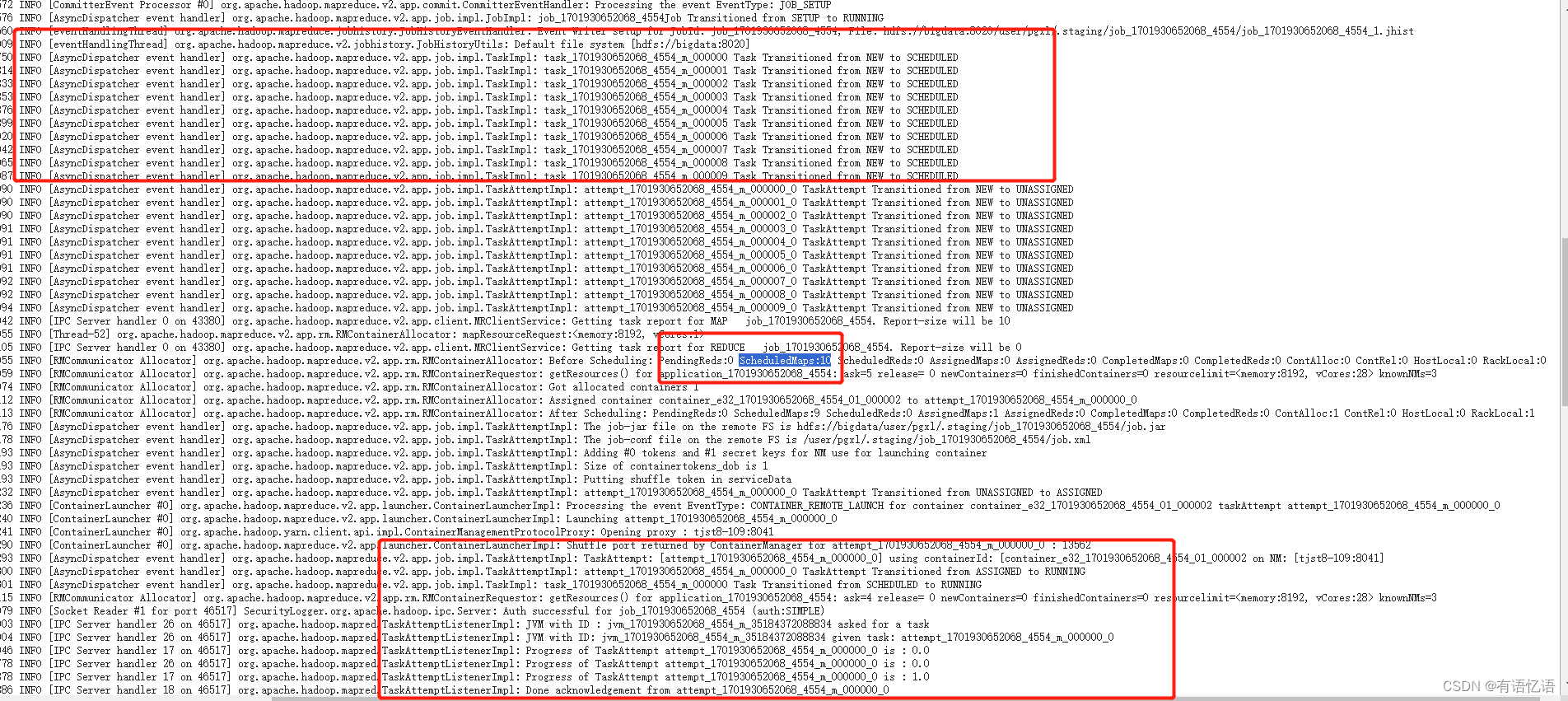
hive映射es表任务失败，无错误日志一直报Task Transitioned from NEW to SCHEDULED
一、背景 要利用gpt产生的存放在es种的日志表做统计分析，通过hive建es的映射表，将es的数据拉到hive里面。 在最初的时候同事写的是全量拉取，某一天突然任务报错，但是没有错误日志一直报：Task Transitioned from NEW t…...
手眼标定 - 最终精度和误差优化心得
手眼标定 - 标定误差优化项 一、TCP标定误差优化1、注意标定针摆放范围2、TCP标定时的点次态与工作姿态尽可能保持相近 二、深度相机对齐矩阵误差1、手动计算对齐矩阵 三、手眼标定拍照姿态1、TCP标定姿态优先2、水平放置棋盘格优先 为减少最终手眼标定的误差，可做或…...
pytorch一致数据增强
分割任务对 image 做（某些）transform 时，要对 label（segmentation mask）也做对应的 transform，如 Resize、RandomRotation 等。如果对 image、label 分别用 transform 处理一遍，则涉及随机操作的…...
MapReduce
1. MapReduce是什么？请简要说明它的工作原理。 MapReduce是一种编程模型，主要用于处理大规模数据集的并行运算，特别是非结构化数据。这个模型的核心思想是将大数据处理任务分解为两个主要步骤：Map和Reduce。用户只需实现map()和r…...
Spring Boot 快速入门
Spring Boot 快速入门 什么是Spring Boot Spring Boot是一个用于简化Spring应用开发的框架，它基于Spring框架，提供了自动配置、快速开发等特性，使得开发者可以更加便捷地构建独立的、生产级别的Spring应用。 开始使用Spring Boot 步骤一&a…...
什么是神经网络的非线性
大家好啊，我是董董灿。 最近在写《计算机视觉入门与调优》（右键，在新窗口中打开链接）的小册，其中一部分说到激活函数的时候，谈到了神经网络的非线性问题。 今天就一起来看看，为什么神经网络需…...
前端知识（十四）——浅谈用户体验测试的主要功能
用户体验(User Experience，简称UX)在现代软件和产品开发中变得愈发重要。为了确保产品能够满足用户期望，提高用户满意度，用户体验测试成为不可或缺的环节。本文将详细探讨用户体验测试的主要功能，以及它在产品开发过程中的重要性 …...
解决前端跨域问题，后端解决方法
Spring CloudVue前后端分离项目报错：Network Error；net::ERR_FAILED（请求跨越）-CSDN博客记录自用...
【网络奇缘系列】计算机网络|数据通信方式|数据传输方式
🌈个人主页: Aileen_0v0🔥系列专栏: 一见倾心,再见倾城 --- 计算机网络~💫个人格言:"没有罗马,那就自己创造罗马~" 这篇文章是关于计算机网络中数据通信的基础知识点， 从模型，术语再到数据通信方式&#…...
数组 注意事项
1.一维数组的初始化 int a[5]{1,2,3,4,5}; 合法 int a[5]{1,2,3}; 合法 int a[]{1,2,3,4,5}; 合法，后面决定前面的大小 int a[5]{1,2,3,4,5,6}; 不合法！ 2.一维数组的定义 int a[5] 合法 int a[11] 合法 int a[1/24] 合法 int x5,a[x…...
day11 滑动窗口中的最大值
class MyQueue { //单调队列（从大到小）public:deque<int> que; // 使用deque来实现单调队列// 每次弹出的时候，比较当前要弹出的数值是否等于队列出口元素的数值，如果相等则弹出。// 同时pop之前判断队列当前是否为空。void…...
XML Group端口详解
在XML数据映射过程中，经常需要对数据进行分组聚合操作。例如，当处理包含多个物料明细的XML文件时，可能需要将相同物料号的明细归为一组，或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码，增加了开…...
国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制，因此这个了16进制的数据既可以翻译成为这个机器码，也可以翻译成为这个国标码，所以这个时候很容易会出现这个歧义的情况； 因此，我们的这个国…...
FastAPI 教程：从入门到实践
FastAPI 是一个现代、快速（高性能）的 Web 框架，用于构建 API，支持 Python 3.6。它基于标准 Python 类型提示，易于学习且功能强大。以下是一个完整的 FastAPI 入门教程，涵盖从环境搭建到创建并运行一个简单的…...
【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装；只需暴露 19530（gRPC）与 9091（HTTP/WebUI）两个端口，即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...
STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA（Direct Memory Access）直接存储器存取 DMA可以提供外设…...
零基础设计模式——行为型模式 - 责任链模式
第四部分：行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习！行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想：使多个对象都有机会处…...
10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI，使用客户端或是内部自己搭建集成大模型的终端，加速与大型语言模型（LLM）的结合，同时使用检索增强生成（Retrieval Augmented Generation &#…...
STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程（限时至2025/5/15） Oracle AI Vector Search 1Z0-184-25考试，都顺利拿到certified了没。 各行各业的AI 大模型的到来，传统的数据库中的SQL还能不能打，结构化和非结构的话数据如何和…...
多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式，给定一个隐函数关系： F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标： 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...