什么是神经网络的非线性
大家好啊,我是董董灿。
最近在写《计算机视觉入门与调优》(右键,在新窗口中打开链接)的小册,其中一部分说到激活函数的时候,谈到了神经网络的非线性问题。
今天就一起来看看,为什么神经网络需要非线性,或者说为什么它是一个非线性系统。
1、线性系统是什么样的
先看一个基础知识:线性函数,这是我们在初中就学过的知识点。
假设有一个线性函数:y = kx + b, 这个函数画出来是下面的样子,也就是说, y 和 x 是线性关系。
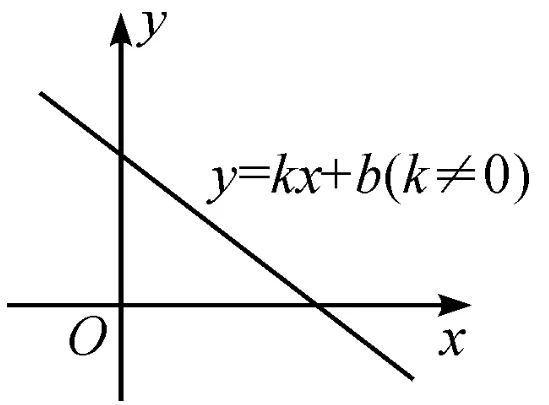
而这个时候如果又有一个线性函数 z = hy + d,那么,我们可以推断出,变量 z 和 x 同样也是线性关系。
为什么呢? 可以通过下面的变换得到。
z = hy + d
= z(kx + b) + d
= zk x + zb + d
= zk(x) + (zb + d)
令 zk = K, zb + d = B,那么 z 和 x 的关系就可以写出 z = Kx + B
所以,z 和 x 同样是线性关系。
这里想说的一个原理是:多个线性系统的叠加,最终还会是线性系统。
2、神经网络是什么系统呢?
回到神经网络,我们知道卷积的算法公式是 y = x * w,,其中 x 是输入数据,w 是权值,中间的 * 代表卷积计算。关于卷积可以查看:5分钟搞懂卷积。
那么x * w 是线性关系还是非线性关系呢?不好意思,就是线性关系。
这是因为卷积的核心计算是乘累加运算,所以,卷积算法也是线性的。
假设神经网络是由大量的卷积算法一层接着一层组成。如果没有非线性因素的引入,那么在数学模型上,这个大的卷积堆砌的模型就会退化成一个简单的线性模型,这就使得多层卷积失去了意义。
层数再多也没用,因为数学上等价于一个卷积,看下图解释的更清楚一些。

这就是原因所在。
所以在很多神经网络模型中,都需要引入非线性因素,从而使得神经网络模型可以拟合成更加复杂多变的非线性系统。
这样模型就可以处理复杂的任务,而不用担心模型在数学上仅仅是一个简单的线性模型了。
怎么引入非线性因素呢?
最常见的方法就是在卷积层后面增加一层非线性的激活层,这也是为什么在很多卷积算法后面,都能看到 relu 函数的原因。
延伸阅读,请参考:神经网络的非线性思想,真的神了。
相关文章:

什么是神经网络的非线性
大家好啊,我是董董灿。 最近在写《计算机视觉入门与调优》(右键,在新窗口中打开链接)的小册,其中一部分说到激活函数的时候,谈到了神经网络的非线性问题。 今天就一起来看看,为什么神经网络需…...
——浅谈用户体验测试的主要功能)
前端知识(十四)——浅谈用户体验测试的主要功能
用户体验(User Experience,简称UX)在现代软件和产品开发中变得愈发重要。为了确保产品能够满足用户期望,提高用户满意度,用户体验测试成为不可或缺的环节。本文将详细探讨用户体验测试的主要功能,以及它在产品开发过程中的重要性 …...

解决前端跨域问题,后端解决方法
Spring CloudVue前后端分离项目报错:Network Error;net::ERR_FAILED(请求跨越)-CSDN博客记录自用...

【网络奇缘系列】计算机网络|数据通信方式|数据传输方式
🌈个人主页: Aileen_0v0🔥系列专栏: 一见倾心,再见倾城 --- 计算机网络~💫个人格言:"没有罗马,那就自己创造罗马~" 这篇文章是关于计算机网络中数据通信的基础知识点, 从模型,术语再到数据通信方式&#…...

数组 注意事项
1.一维数组的初始化 int a[5]{1,2,3,4,5}; 合法 int a[5]{1,2,3}; 合法 int a[]{1,2,3,4,5}; 合法,后面决定前面的大小 int a[5]{1,2,3,4,5,6}; 不合法! 2.一维数组的定义 int a[5] 合法 int a[11] 合法 int a[1/24] 合法 int x5,a[x…...

day11 滑动窗口中的最大值
class MyQueue { //单调队列(从大到小)public:deque<int> que; // 使用deque来实现单调队列// 每次弹出的时候,比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。// 同时pop之前判断队列当前是否为空。void…...
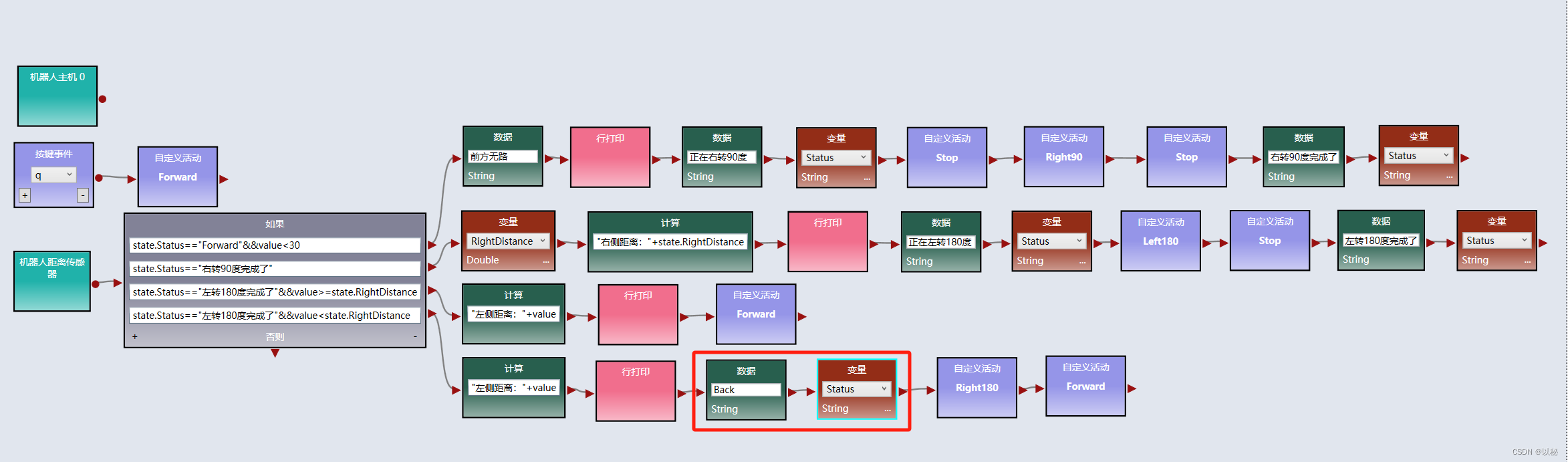
viple模拟器使用(五):Web 2D模拟器中实现两距离局部最优迷宫算法
关于两距离局部最优迷宫算法的原理本文不再赘述,详情请参考:viple模拟器使用(四),归纳总结为: 前方有路,则直行; 前方无路,则右转90度,标记右转完成ÿ…...
)
每日一道算法题 3(2023-12-11)
题目描述: VLAN是一种对局域网设备进行逻辑划分的技术,为了标识不同的VLAN,引入VLAN ID(1-4094之间的整数)的概念。 定义一个VLAN ID的资源池(下称VLAN资源池),资源池中连续的VLAN用开始VLAN-结束VLAN表示,不连续的用单…...
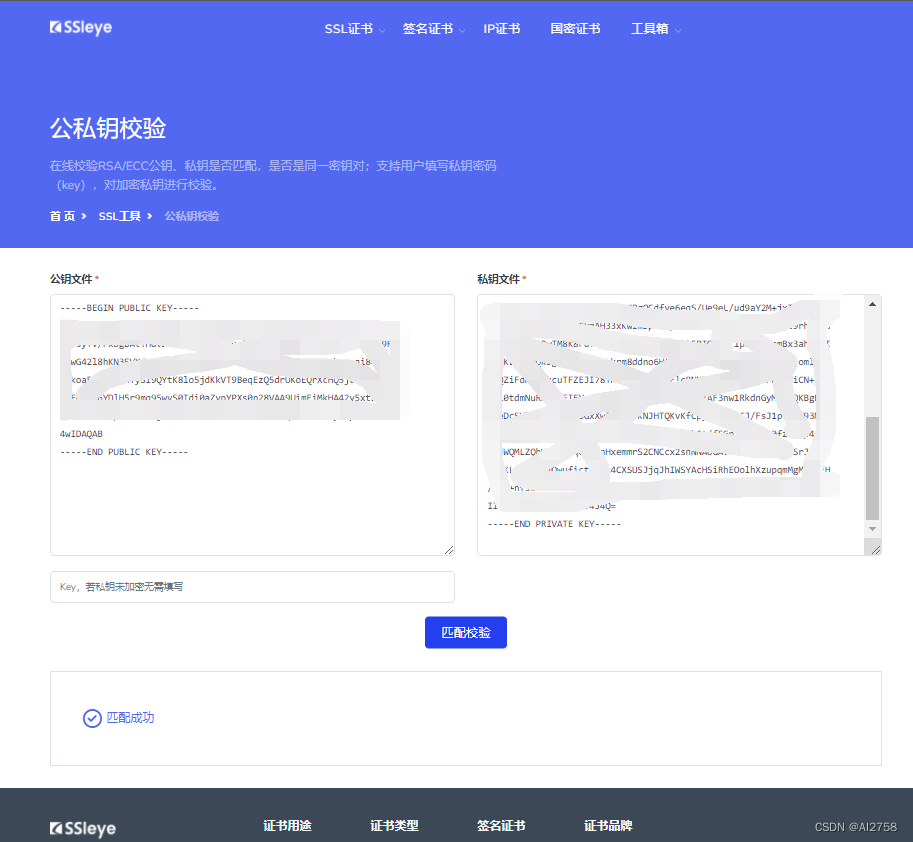
【Android】查看keystore的公钥和私钥
前言: 查看前准备好.keystore文件,安装并配置openssl、keytool。文件路径中不要有中文。 一、查看keystore的公钥: 1.从keystore中获取MD5证书 keytool -list -v -keystore gamekeyold.keystore 2.导出公钥文件 keytool -export -alias …...

ChatGPT的常识
什么是ChatGPT? ChatGPT是一个基于GPT模型的聊天机器人,GPT即“Generative Pre-training Transformer”,是一种预训练的语言模型。ChatGPT使用GPT-2和GPT-3两种模型来生成自然语言响应,从而与人类进行真实的对话。 ChatGPT的设计…...

Spring Boot中的事务是如何实现的?懂吗?
SpringBoot中的事务管理,用得好,能确保数据的一致性和完整性;用得不好,可能会给性能带来不小的影响哦。 基本使用 在SpringBoot中,事务的使用非常简洁。首先,得感谢Spring框架提供的Transactional注解&am…...

应用安全:JAVA反序列化漏洞之殇
应用安全:JAVA反序列化漏洞之殇 概述 序列化是让Java对象脱离Java运行环境的一种手段,可以有效的实现多平台之间的通信、对象持久化存储。Java 序列化是指把 Java 对象转换为字节序列的过程便于保存在内存、文件、数据库中,ObjectOutputStream类的 wri…...
)
基于以太坊的智能合约开发Solidity(函数继承篇)
参考教程:【实战篇】1、函数重载_哔哩哔哩_bilibili 1、函数重载: pragma solidity ^0.5.17;contract overLoadTest {//不带参数function test() public{}//带一个参数function test(address account) public{}//参数类型不同,虽然uint160可…...

【论文极速读】LVM,视觉大模型的GPT时刻?
【论文极速读】LVM,视觉大模型的GPT时刻? FesianXu 20231210 at Baidu Search Team 前言 这一周,LVM在arxiv上刚挂出不久,就被众多自媒体宣传为『视觉大模型的GPT时刻』,笔者抱着强烈的好奇心,在繁忙工作之…...

TS基础语法
前言: 因为在写前端的时候,发现很多UI组件的语法都已经开始使用TS语法,不学习TS根本看不到懂,所以简单的学一下TS语法。为了看UI组件的简单代码,不至于一脸懵。 一、安装node 对于windows来讲,node版本高…...

【基于NLP的微博情感分析:从数据爬取到情感洞察】
基于NLP的微博情感分析:从数据爬取到情感洞察 背景数据集技术选型功能实现创新点 今天我将分享一个基于NLP的微博情感分析项目,通过Python技术、NLP模型和Flask框架,对微博数据进行清洗、分词、可视化,并利用NLP和贝叶斯进行情感分…...

Ubuntu 18.04使用Qemu和GDB搭建运行内核的环境
安装busybox 参考博客: 使用GDBQEMU调试Linux内核环境搭建 一文教你如何使用GDBQemu调试Linux内核 ubuntu22.04搭建qemu环境测试内核 交叉编译busybox 编译busybox出现Library m is needed, can’t exclude it (yet)的解释 S3C2440 制作最新busybox文件系统 https:…...

GEE——利用Landsat系列数据集进行1984-2023EVI指数趋势分析
简介: 利用Landsat系列数据集进行1984-2023EVI指数趋势分析其主要目的是进行长时序的分析,这里我们选用EVI指数,然后进行了4个月的分析,查看其最后的线性趋势以及分布状况。 EVI指数: EVI指数(Enhanced Vegetation Index,增强型植被指数)是一种反映植被生长状态的遥…...
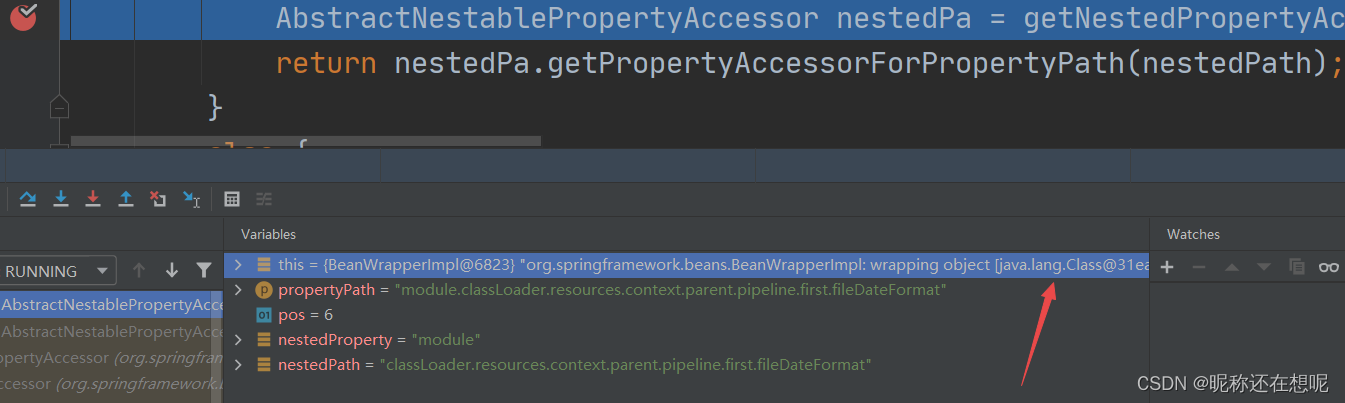
JAVA安全之Spring参数绑定漏洞CVE-2022-22965
前言 在介绍这个漏洞前,介绍下在spring下的参数绑定 在Spring框架中,参数绑定是一种常见的操作,用于将HTTP请求的参数值绑定到Controller方法的参数上。下面是一些示例,展示了如何在Spring中进行参数绑定: 示例1&am…...

辨析旅行商问题(TSP)与车辆路径问题(VRP)
目录 前言旅行商问题 (TSP)问题介绍数学模型符号定义问题输入约束条件目标函数问题输出 解的空间解空间大小计算解释 车辆路径问题 (VRP)问题介绍TSP到VRP的过渡数学模型符号定义问题输入约束条件优化目标问题输出 解空间特殊情况一般情况 TSP 与 VRP 对比 前言 计划是通过本文…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...
