【高数:3 无穷小与无穷大】
【高数:3 无穷小与无穷大】
- 1 无穷小与无穷大
- 2 极限运算法则
- 3 极限存在原则
- 4 趋于无穷小的比较
参考书籍:毕文斌, 毛悦悦. Python漫游数学王国[M]. 北京:清华大学出版社,2022.
1 无穷小与无穷大
无穷大在sympy中用两个字母o表示无穷大,正无穷大为sy.oo,负无穷大为-sy.oo
import sympy as sy
x=sy.oo
print(1/x)
>>>0
lim x → 0 − 1 x \lim_{x \to 0^-} \frac{1}{x} limx→0−x1
x=sy.symbols('x')
print(sy.limit(1/x,x,0,dir='-'))
>>>-oo
2 极限运算法则
lim x → 3 x − 3 x 2 − 9 \lim_{x \to 3} \frac{x-3}{x^2-9} limx→3x2−9x−3
import sympy as sy
x=sy.symbols('x')
print(sy.limit((x-3)/(x**2-9),x,3,dir='+-'))
lim x → 1 2 x − 3 x 2 − 5 x + 4 \lim_{x \to 1} \frac{2x-3}{x^2-5x+4} limx→1x2−5x+42x−3
x=sy.symbols('x')
print(sy.limit((2*x-3)/(x**2-5*x+4),x,1,dir='-'))
print(sy.limit((2*x-3)/(x**2-5*x+4),x,1))
>>>-oo, oo 故趋于无穷时极限为无穷oo
lim x → ∞ 3 x 3 + 4 X 2 + 2 7 x 3 + 5 x 2 − 3 \lim_{x \to \infty} \frac{3x^3+4X^2+2}{7x^3+5x^2-3} limx→∞7x3+5x2−33x3+4X2+2
x=sy.symbols('x')
print(sy.limit((3*x**3+4*x**2+2)/(7*x**3+5*x**2-3),x,sy.oo,dir='-'))
print(sy.limit((3*x**3+4*x**2+2)/(7*x**3+5*x**2-3),x,-sy.oo,dir='+'))
>>>3/7,3/7 故趋于无穷时极限为3/7
当分子分母极限都不存在时, lim x → ∞ sin x x \lim_{x \to \infty} \frac{\sin x}{x} limx→∞xsinx
x=sy.symbols('x')
y=sy.sin(x)/x
print(sy.limit(y,x,sy.oo,dir='+'))
print(sy.limit(y,x,-sy.oo,dir='+'))
>>>0 , 0 故趋于无穷时极限为0
3 极限存在原则
eg1: lim x → 0 sin x x \lim_{x \to 0} \frac{\sin x}{x} limx→0xsinx
import sympy as sy
x=sy.symbols('x')
lim=sy.limit(sy.sin(x)/x,x,0,dir='+-')
print(lim)
>>>1
eg2: lim x → 0 arcsin x tan x \lim_{x \to 0} \frac{\arcsin x}{\tan x} limx→0tanxarcsinx
x=sy.symbols('x')
print(sy.limit(sy.asin(x)/sy.tan(x),x,0,dir='+-')) #sy.asin()指arcsin函数
>>>1
eg3: lim x → 0 1 − cos x x 2 \lim_{x \to 0} \frac{1- \cos x}{x^2} limx→0x21−cosx
x=sy.symbols('x')
print(sy.limit((1-sy.cos(x))/(x**2),x,0,dir='+-'))
>>>1/2
eg4: lim x → 0 ( 1 + x ) 1 x \lim_{x \to 0} (1+x)^{\frac{1}{x}} limx→0(1+x)x1
x=sy.symbols('x')
lim=sy.limit((1+x)**(1/x),x,0,dir='+-')
print(lim)
>>>E
eg5: lim x → ∞ ( 1 + 1 x ) x \lim_{x \to \infty} (1+\frac{1}{x})^x limx→∞(1+x1)x
x=sy.symbols('x')
lim=sy.limit((1+1/x)**x,x,sy.oo,dir='-')
print(lim)
print(lim.round(3))
print(sy.limit((1+1/x)**x,x,-sy.oo))
>>>E, 2.718, E
eg6: 说明数列 2 , 2 + 2 , 2 + 2 + 2 \sqrt{2} , \sqrt{2+\sqrt{2}},\sqrt{2+\sqrt{2+\sqrt{2}}} 2,2+2,2+2+2,···的极限存在
#用函数的递归机制定义数列
def a_complex_series(n):#退出条件if n<=0:return 2**0.5#一个函数如果调用自身,则这个函数就是一个递归函数return (2.0+a_complex_series(n-1))**0.5
#绘制前20个数的散点图
import matplotlib.pyplot as plt
import numpy as np
x=[]
y=[]
for i in range(20):x.append(i)y.append(a_complex_series(i))
print(np.array(y))
plt.scatter(x,y)
plt.show()
>>>[1.41421356 1.84775907 1.96157056 1.99036945 1.99759091 1.99939764
1.9998494 1.99996235 1.99999059 1.99999765 1.99999941 1.999999851.99999996 1.99999999 2. 2. 2. 2.
2. 2. ]

故极限为2
4 趋于无穷小的比较
eg1: lim x → 0 tan 2 x sin 5 x \lim_{x \to 0} \frac{\tan 2x}{\sin 5x} limx→0sin5xtan2x
from sympy import limit,sin,cos,tan,symbols #从sympy中仅导入这几个函数
x=symbols('x')
example_1=tan(2*x)/sin(5*x)
result=limit(example_1,x,0,dir='+-')
print(result)
>>>2/5
eg2: lim x → 0 sin x x 3 + 3 x \lim_{x \to 0} \frac{\sin x}{x^3+3x} limx→0x3+3xsinx
x=symbols('x')
example_2=sin(x)/(x**3+3*x)
result=limit(example_2,x,0,dir='+-')
print(result)
>>>1/3
eg3: lim x → 0 ( 1 + x 2 ) 1 / 3 − 1 cos x − 1 \lim_{x \to 0} \frac{(1+x^2)^{1/3}-1}{\cos x-1} limx→0cosx−1(1+x2)1/3−1
x=symbols('x')
example_3=((1+x**2)**(1/3)-1)/(cos(x)-1)
result=limit(example_3,x,0,dir='+-')
print(result)
>>>-2/3
相关文章:

【高数:3 无穷小与无穷大】
【高数:3 无穷小与无穷大】 1 无穷小与无穷大2 极限运算法则3 极限存在原则4 趋于无穷小的比较 参考书籍:毕文斌, 毛悦悦. Python漫游数学王国[M]. 北京:清华大学出版社,2022. 1 无穷小与无穷大 无穷大在sympy中用两个字母o表示无…...

C语言预读取技术 __builtin_prefetch
__builtin_prefetch 是一个编译器内置函数,用于在编译时向编译器发出指令,要求在执行期间预取内存数据。它通常用于提高程序的性能,特别是对于那些需要频繁访问内存的情况。 __builtin_prefetch 函数的语法如下:c __builtin_prefe…...
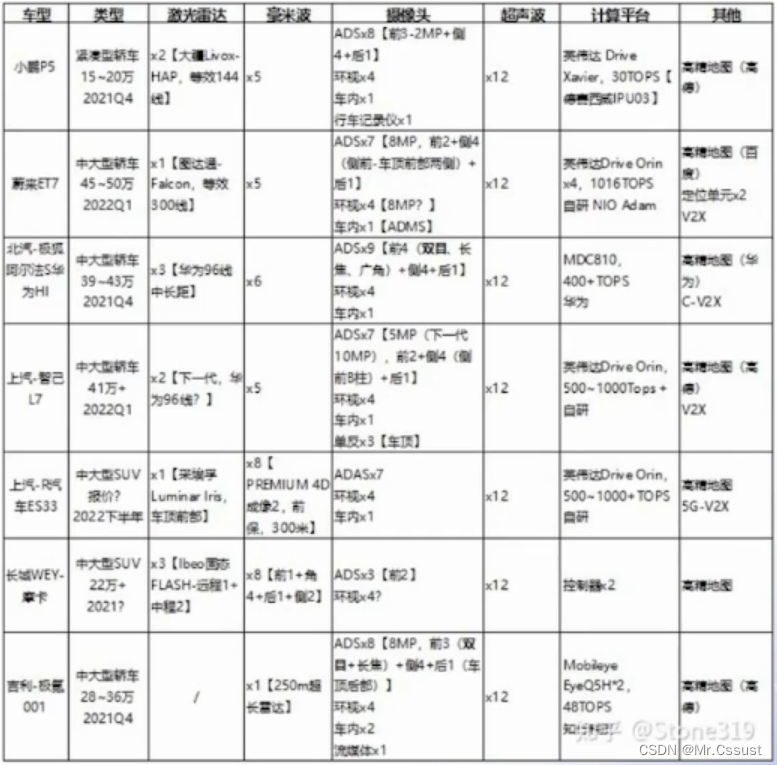
自动驾驶学习笔记(十三)——感知基础
#Apollo开发者# 学习课程的传送门如下,当您也准备学习自动驾驶时,可以和我一同前往: 《自动驾驶新人之旅》免费课程—> 传送门 《Apollo Beta宣讲和线下沙龙》免费报名—>传送门 文章目录 前言 传感器 测距原理 坐标系 标定 同…...
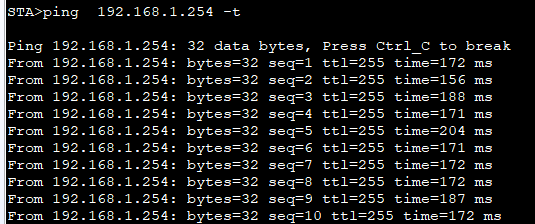
WLAN配置实验
本文记录了WLAN配置实践的过程,该操作在华为HCIA中属于相对较复杂的实验,记录过程备忘。这里不就WLAN原理解释,仅进行配置实践,可以作为学习原理时候的参考。本文使用华为ENSP进行仿真。实验拓扑图如下: 1.WLAN工作流程…...

java_web接收前端传的excel文件读取数据
#本次做一个将患者数据导入到某个模块的功能,前期集成的代码时不时出现异常,本次进行修改记录 //controller层/*** 导入患者数据*/RejectReplayRequestPostMapping("/importData")public Result<?> importData(HttpServletRequest req…...

在Vue开发中v-if指令和v-show指令的使用介绍和区别及使用场景
一、条件渲染 v-if v-if 指令用于条件性地渲染一块内容。这块内容只会在指令的表达式返回真值时才被渲染。 <h1 v-if"awesome">Vue is awesome!</h1>v-else 你也可以使用 v-else 为 v-if 添加一个“else 区块”。 <h1 v-if"awesome"&g…...

Power Query是啥
Power Query是一种用于数据获取、转换和整理的功能强大的工具,它是Microsoft Excel和Power BI中的一个组件。Power Query可以帮助用户从各种数据源中获取数据,并进行数据清洗、转换和整理,以便进一步分析和可视化。 使用Power Query…...

在k8s中部署nfs-client-provisioner
1、部署过程 1.1、环境依赖 在部署nfs-client-provisioner之前,需要先部署nfs服务。 因为,nfs-client-provisioner创建的pv都是要在nfs服务器中搭建的。 本示例中的nfs server的地址如下: [rootnode1 /]# showmount -e Export list for …...
23.12.10日总结
周总结 这周三的晚自习,学姐讲了一下git的合作开发,还有懒加载,防抖,节流 答辩的时候问了几个问题: 为什么在js中0.10.2!0.3? 在js中进行属性运算时,会出现0.10.20.300000000000000004js遵循IEEE754标…...
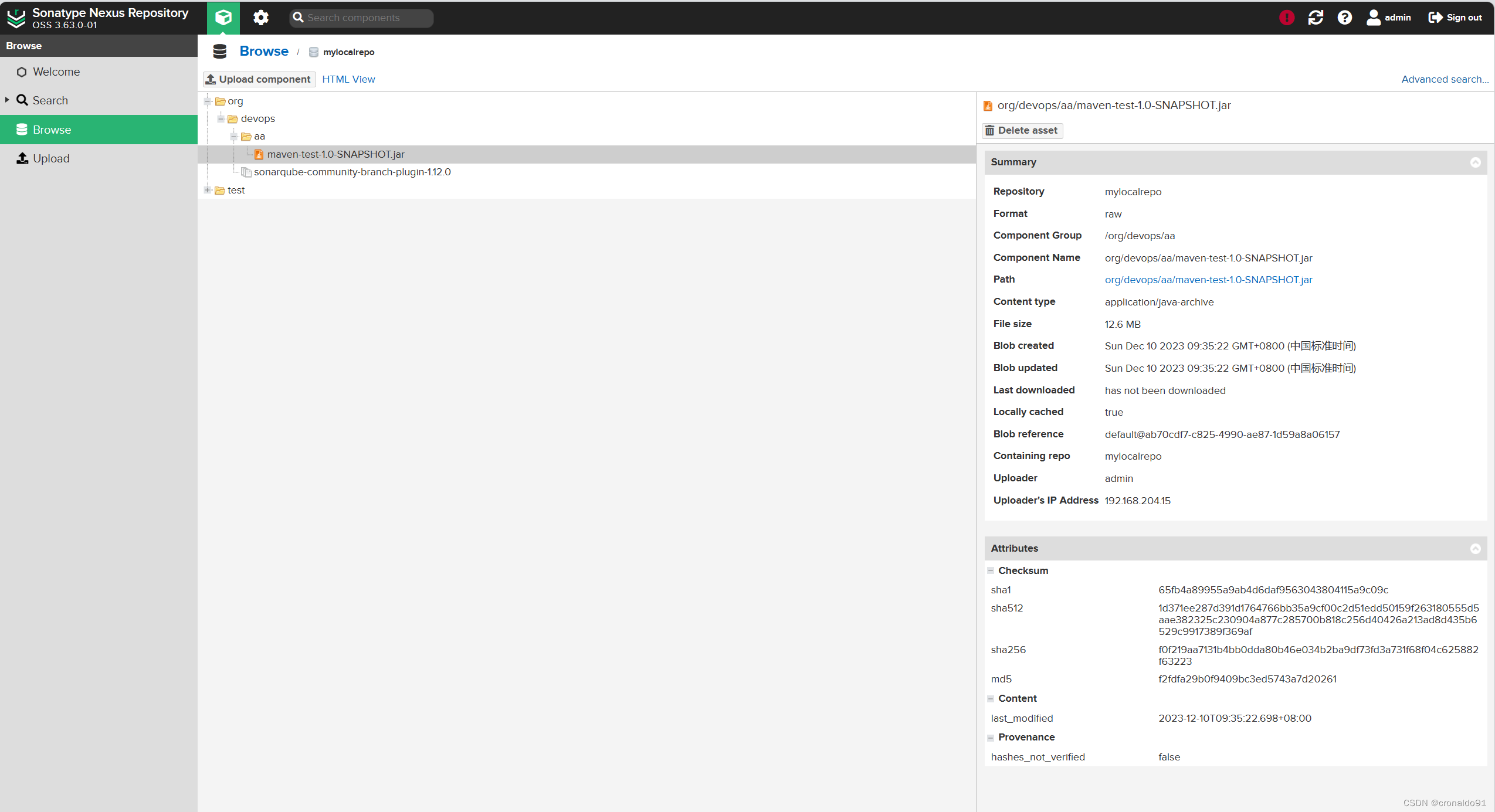
持续集成交付CICD:通过API方式上传Nexus制品
目录 一、实验 1.通过API方式上传Nexus制品 二、问题 1.如何通过API方式上传PNG图片 2.如何通过API方式上传tar.gz 与 ZIP文件 3.如何通过API方式上传Jar file文件 4.如何通过API方式上传制品(maven类型的制品)文件 5.如何下载制品 一、实验 1.通…...

Hadoop学习笔记(HDP)-Part.14 安装YARN+MR
目录 Part.01 关于HDP Part.02 核心组件原理 Part.03 资源规划 Part.04 基础环境配置 Part.05 Yum源配置 Part.06 安装OracleJDK Part.07 安装MySQL Part.08 部署Ambari集群 Part.09 安装OpenLDAP Part.10 创建集群 Part.11 安装Kerberos Part.12 安装HDFS Part.13 安装Ranger …...
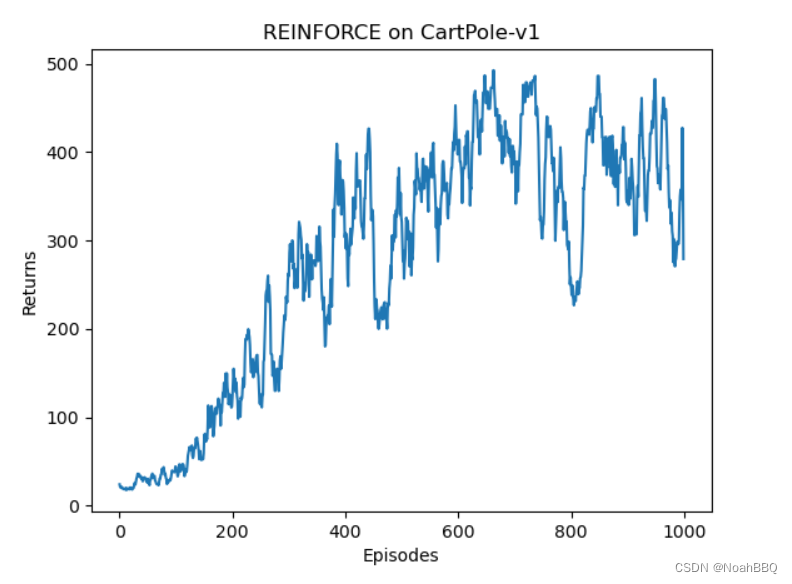
reinforce 跑 CartPole-v1
gym版本是0.26.1 CartPole-v1的详细信息,点链接里看就行了。 修改了下动手深度强化学习对应的代码。 然后这里 J ( θ ) J(\theta) J(θ)梯度上升更新的公式是用的不严谨的,这个和王树森书里讲的严谨公式有点区别。 代码 import gym import torch from …...
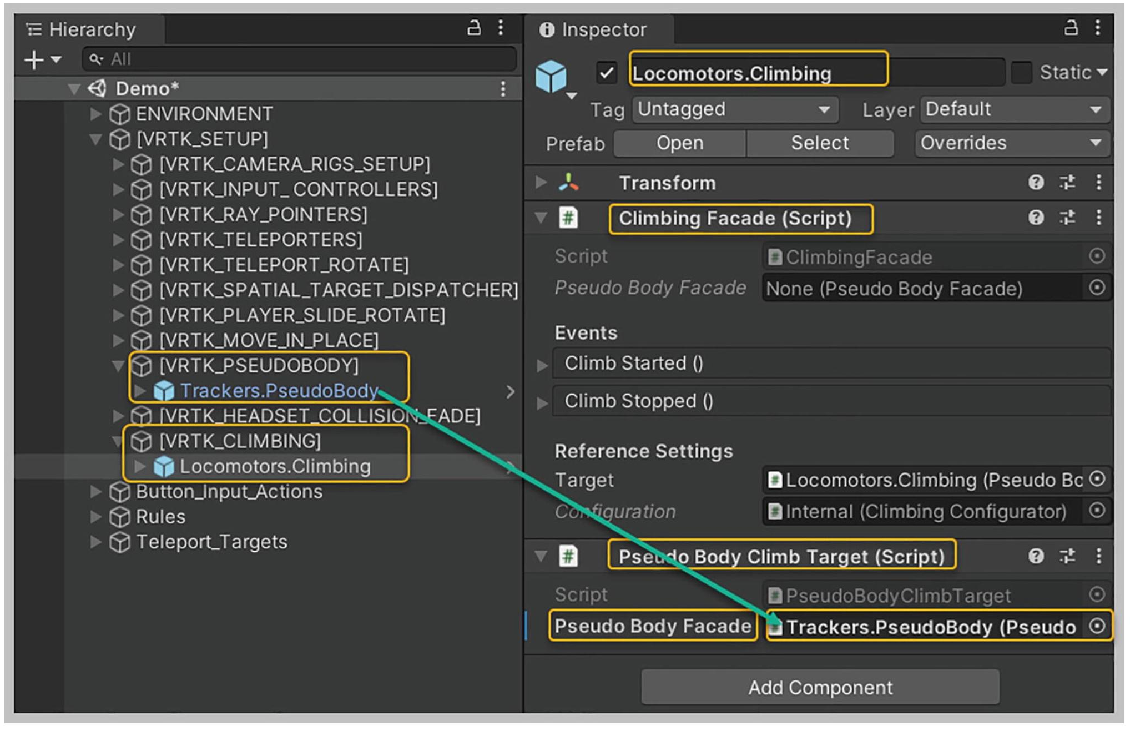
【VRTK】【VR开发】【Unity】13-攀爬
课程配套学习资源下载 https://download.csdn.net/download/weixin_41697242/88485426?spm=1001.2014.3001.5503 【概述】 VRTK提供两个预制件实现攀爬 Climbing Controller,用于控制Player的物理义体Climbable Interactable,用于设置可攀爬对象【设置Climbing Controller…...
)
华为OD机试真题-求幸存数之和-2023年OD统一考试(C卷)
题目描述: 给一个正整数列 nums,一个跳数 jump,及幸存数量 left。运算过程为:从索引为0的位置开始向后跳,中间跳过 J 个数字,命中索引为J1的数字,该数被敲出,并从该点起跳ÿ…...
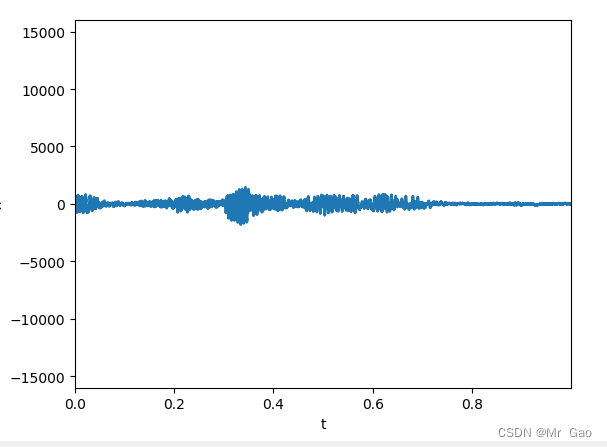
python pyaudio实时读取音频数据并展示波形图
python pyaudio实时读取音频数据并展示波形图 下面代码可以驱动电脑接受声音数据,并实时展示音波图: import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation import pyaudio import wave import os import op…...
【算法系列篇】递归、搜索和回溯(二)
文章目录 前言1. 两两交换链表中的节点1.1 题目要求1.2 做题思路1.3 代码实现 2. Pow(X,N)2.1 题目要求2.2 做题思路2.3 代码实现 3. 计算布尔二叉树的值3.1 题目要求3.2 做题思路3.3 代码实现 4. 求根节点到叶结点数字之和4.1 题目要求4.2 做题思路4.3 代码实现 前言 前面为大…...

Ubuntu下安装SDL
源码下载地址(SDL version 2.0.14):https://www.libsdl.org/release/SDL2-2.0.14.tar.gz 将源码包拷贝到系统里 使用命令解压 tar -zxvf SDL2-2.0.14.tar.gz 解压得到文件夹 SDL2-2.0.14 进入文件夹 执行命令 ./configure 执行命令 make…...

创建vue项目:vue脚手架安装、vue-cli安装,vue ui界面创建vue工程(vue2/vue3),安装vue、搭建vue项目开发环境(保姆级教程二)
今天讲解 Windows 如何利用脚手架创建 vue 工程,以及 vue ui 图形化界面搭建 vue 开发环境,这是这个系列的第二章,有什么问题请留言,请点赞收藏!!! 文章目录 1、安装vue-cli脚手架2、vue ui创建…...
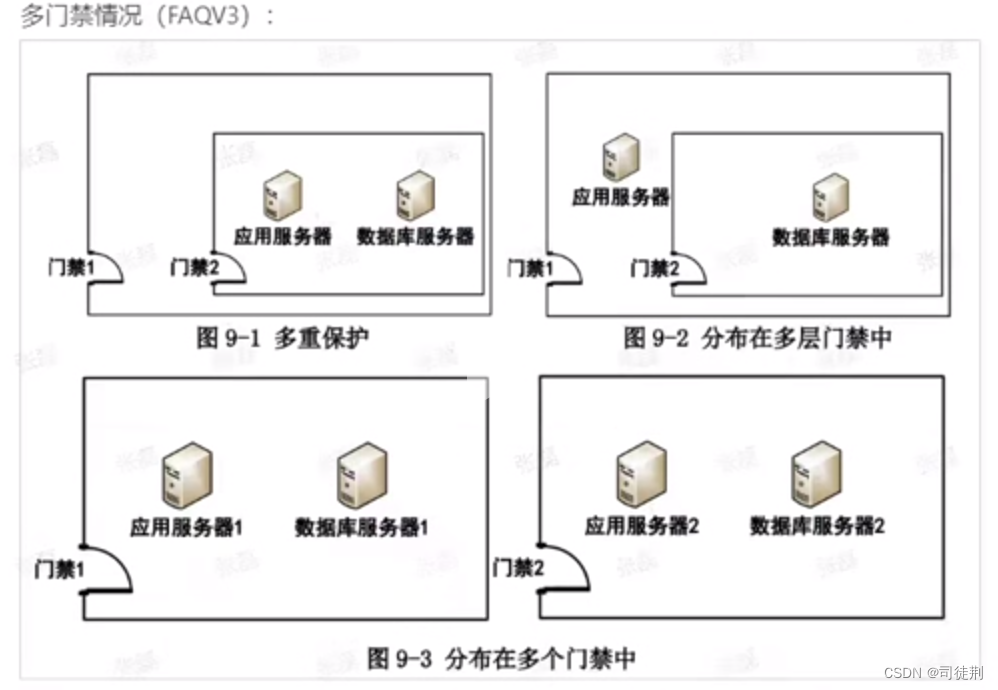
【3】密评-物理和环境安全测评
0x01 依据 GB/T 39786 -2021《信息安全技术 信息系统密码应用基本要求》针对等保三级系统要求: 物理和环境层面: a)宜采用密码技术进行物理访问身份鉴别,保证重要区域进入人员身份的真实性; b)宜采用密码技术保证电子门…...

笨爸爸工房,我们在校园|“小鲁班”,铸未来
为了响应国家号召,将劳动教育课程真正实现融入校园生活,笨爸爸工房已与洛阳市西下池小学、洛阳市第一实验小学西工校区、洛阳市西工区第二实验小学、洛阳第二外国语学校(兰溪校区)、洛阳市睿源幼儿园,这4所学校及1家幼…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...
