[足式机器人]Part2 Dr. CAN学习笔记-数学基础Ch0-5Laplace Transform of Convolution卷积的拉普拉斯变换
本文仅供学习使用
本文参考:
B站:DR_CAN
Dr. CAN学习笔记-数学基础Ch0-5Laplace Transform of Convolution卷积的拉普拉斯变换
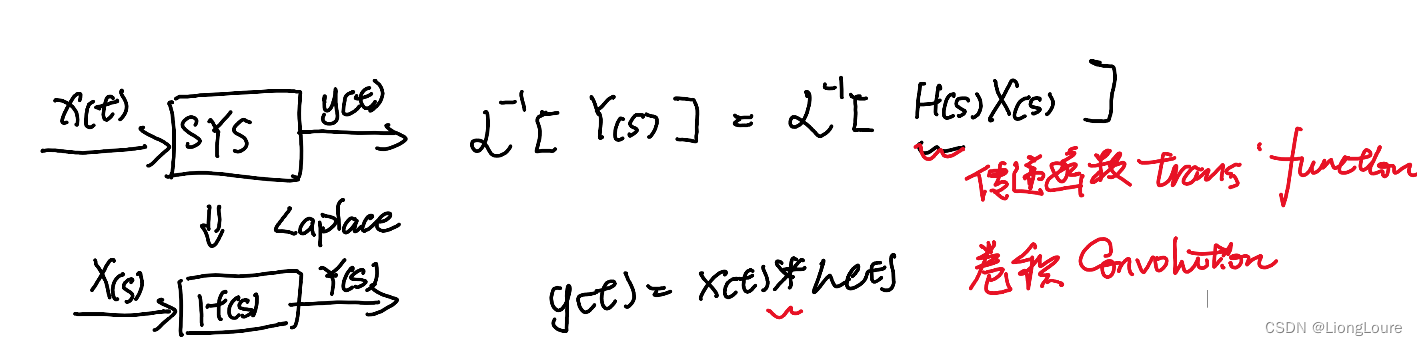
Laplace Transform : X ( s ) = L [ x ( t ) ] = ∫ 0 ∞ x ( t ) e − s t d t X\left( s \right) =\mathcal{L} \left[ x\left( t \right) \right] =\int_0^{\infty}{x\left( t \right) e^{-st}}\mathrm{d}t X(s)=L[x(t)]=∫0∞x(t)e−stdt
Convolution : x ( t ) ∗ g ( t ) = ∫ 0 t x ( τ ) g ( t − τ ) d τ x\left( t \right) *g\left( t \right) =\int_0^t{x\left( \tau \right) g\left( t-\tau \right)}\mathrm{d}\tau x(t)∗g(t)=∫0tx(τ)g(t−τ)dτ
证明: L [ x ( t ) ∗ g ( t ) ] = X ( s ) G ( s ) \mathcal{L} \left[ x\left( t \right) *g\left( t \right) \right] =X\left( s \right) G\left( s \right) L[x(t)∗g(t)]=X(s)G(s)
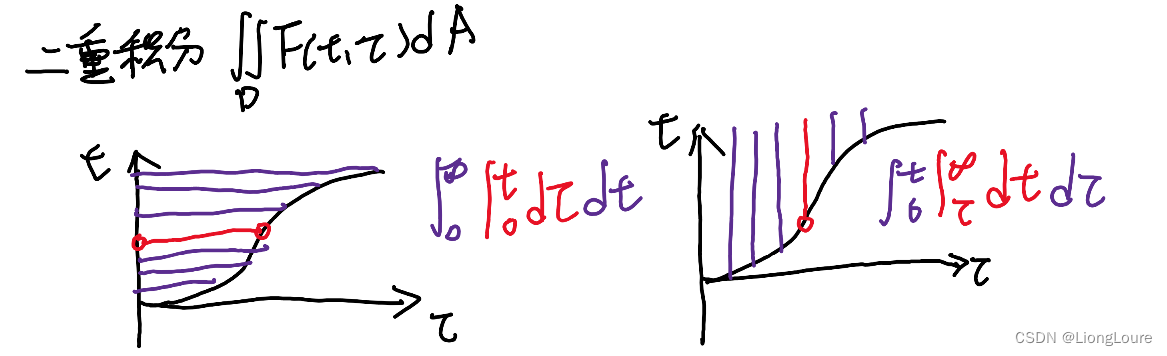
L [ x ( t ) ∗ g ( t ) ] = ∫ 0 ∞ ∫ 0 t x ( τ ) g ( t − τ ) d τ e − s t d t = ∫ 0 ∞ ∫ τ ∞ x ( τ ) g ( t − τ ) e − s t d t d τ \mathcal{L} \left[ x\left( t \right) *g\left( t \right) \right] =\int_0^{\infty}{\int_0^t{x\left( \tau \right) g\left( t-\tau \right) \mathrm{d}\tau}e^{-st}}\mathrm{d}t=\int_0^{\infty}{\int_{\tau}^{\infty}{x\left( \tau \right) g\left( t-\tau \right)}e^{-st}}\mathrm{d}t\mathrm{d}\tau L[x(t)∗g(t)]=∫0∞∫0tx(τ)g(t−τ)dτe−stdt=∫0∞∫τ∞x(τ)g(t−τ)e−stdtdτ
>令: u = t − τ , t = u + τ , d t = d u + d τ , t ∈ [ τ , + ∞ ) ⇒ u ∈ [ 0 , + ∞ ) u=t-\tau ,t=u+\tau ,\mathrm{d}t=\mathrm{d}u+\mathrm{d}\tau ,t\in \left[ \tau ,+\infty \right) \Rightarrow u\in \left[ 0,+\infty \right) u=t−τ,t=u+τ,dt=du+dτ,t∈[τ,+∞)⇒u∈[0,+∞)
L [ x ( t ) ∗ g ( t ) ] = ∫ 0 ∞ ∫ 0 ∞ x ( τ ) g ( u ) e − s ( u + τ ) d u d τ = ∫ 0 ∞ x ( τ ) e − s τ d τ ∫ 0 ∞ g ( u ) e − s u d u = X ( s ) G ( s ) \mathcal{L} \left[ x\left( t \right) *g\left( t \right) \right] =\int_0^{\infty}{\int_0^{\infty}{x\left( \tau \right) g\left( u \right)}e^{-s\left( u+\tau \right)}}\mathrm{d}u\mathrm{d}\tau =\int_0^{\infty}{x\left( \tau \right)}e^{-s\tau}\mathrm{d}\tau \int_0^{\infty}{g\left( u \right)}e^{-su}\mathrm{d}u=X\left( s \right) G\left( s \right) L[x(t)∗g(t)]=∫0∞∫0∞x(τ)g(u)e−s(u+τ)dudτ=∫0∞x(τ)e−sτdτ∫0∞g(u)e−sudu=X(s)G(s)
L [ x ( t ) ∗ g ( t ) ] = L [ x ( t ) ] L [ g ( t ) ] = X ( s ) G ( s ) \mathcal{L} \left[ x\left( t \right) *g\left( t \right) \right] =\mathcal{L} \left[ x\left( t \right) \right] \mathcal{L} \left[ g\left( t \right) \right] =X\left( s \right) G\left( s \right) L[x(t)∗g(t)]=L[x(t)]L[g(t)]=X(s)G(s)
相关文章:
[足式机器人]Part2 Dr. CAN学习笔记-数学基础Ch0-5Laplace Transform of Convolution卷积的拉普拉斯变换
本文仅供学习使用 本文参考: B站:DR_CAN Dr. CAN学习笔记-数学基础Ch0-5Laplace Transform of Convolution卷积的拉普拉斯变换 Laplace Transform : X ( s ) L [ x ( t ) ] ∫ 0 ∞ x ( t ) e − s t d t X\left( s \right) \mathcal{L} \left[ x\lef…...
生产问题: 利用线程Thread预加载数据缓存,其它类全局变量获取缓存偶发加载不到
生产问题: 利用线程Thread预加载数据缓存偶发加载不到 先上代码 public class ThreadTest {//本地缓存Map<String, Object> map new HashMap<String, Object>();class ThreadA implements Runnable{Overridepublic void run() {System.out.println("Thread…...

Elasticsearch mapping 之 性能相关配置
ES 常见类型 通用类型: 二进制: binary 布尔型: boolean 字符串: keyword, constant_keyword, wildcard, text 别名: alias 对象: object, flattened, nested, join 结构化数据类型: Range, ip, version, murmur3 空间数据类型: geo_point, geo_shape, point, shape 性…...

adb push报错:remote couldn‘t create file: Is a directory
adb push报错:remote couldn‘t create file: Is a directory 出现这个问题可能是电脑本地目录中包含中文或者是目录地址中多包含了一个/ 比如说以下两种路径 1. test/测试音频文件1/a.mp3 2.test/test_audio/ 这两种都是不可以的(我是在as中执行的…...

GitLab 服务更换了机器,IP 地址或域名没有变化时,可能会出现无法拉取或提交代码的情况。
当 GitLab 服务更换了机器,但 IP 地址或域名没有变化时,可能会出现无法拉取或提交代码的情况。 这可能是由于 SSH 密钥或 SSL 证书发生了变化。以下是一些可能的解决步骤: 这可能是由于 SSH 密钥或 SSL 证书发生了变化。以下是一些可能的解决…...

【华为OD题库-076】执行时长/GPU算力-Java
题目 为了充分发挥GPU算力,需要尽可能多的将任务交给GPU执行,现在有一个任务数组,数组元素表示在这1秒内新增的任务个数且每秒都有新增任务。 假设GPU最多一次执行n个任务,一次执行耗时1秒,在保证GPU不空闲情况下&…...

持续集成交付CICD:Jenkins使用GitLab共享库实现前后端项目Sonarqube
目录 一、实验 1.Jenkins使用GitLab共享库实现后端项目Sonarqube 2.优化GitLab共享库 3.Jenkins使用GitLab共享库实现前端项目Sonarqube 4.Jenkins通过插件方式进行优化 二、问题 1.sonar-scanner 未找到命令 2.npm 未找到命令 一、实验 1.Jenkins使用GitLab共享库实现…...
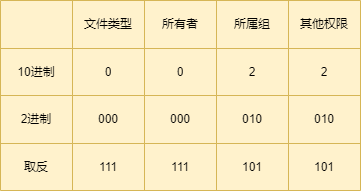
Linux文件结构与文件权限
基于centos了解Linux文件结构 了解一下文件类型 Linux采用的一切皆文件的思想,将硬件设备、软件等所有数据信息都以文件的形式呈现在用户面前,这就使得我们对计算机的管理更加方便。所以本篇文章会对Linux操作系统的文件结构和文件权限进行讲解。 首先…...

CentOS上安装和配置Apache HTTP服务器
在CentOS系统上安装和配置Apache HTTP服务器可以为您的网站提供可靠的托管环境。Apache是开源的Web服务器软件,具有广泛的支持和强大的功能。下面是在CentOS上安装和配置Apache HTTP服务器的步骤: 步骤一:安装Apache HTTP服务器 打开终端&am…...
———ES6迭代器)
前端知识(十二)———ES6迭代器
ES6中的迭代器是一种新的对象,它具有一个next()方法。next()方法返回一个对象,这个对象包含两个属性:value和done。value属性是迭代器中的下一个值,done属性是一个布尔值,表示迭代器是否已经遍历完所有的值。迭代器是一…...
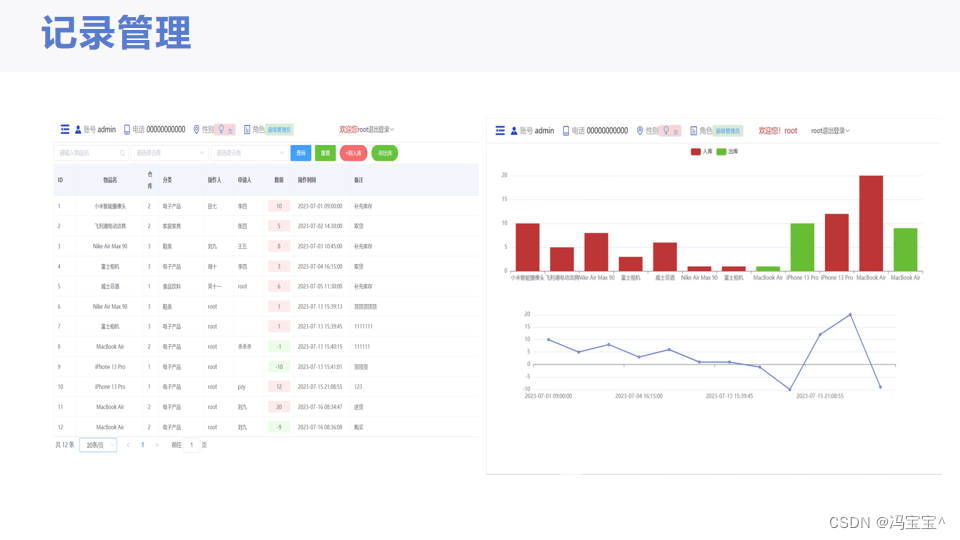
云端仓库平台
SpringBoot MySQL Vue 等技术实现的云端仓库 技术栈 核心框架:SpringBoot 持久层框架:MyBatis-Plus 前端框架:Vue 数据库:MySQL 项目包含源码和数据库文件。 效果图如下:...

php第三方skd自动加载
把mugou-sdk复制到项目下在composer.josn找到classmap加入sdk "autoload": {"classmap": ["mugou-sdk"] },在composer.josn找到files加入sdk "autoload": {"files":[mugou-sdk] },项目目录下运行 composer dump-autoload…...

Golang channle(管道)基本介绍、快速入门
channel(管道)-基本介绍 为什么需要channel?前面使用全局变量加锁同步来解决goroutine的通讯,但不完美 1)主线程在等待所有goroutine全部完成的时间很难确定,我们这里设置10秒,仅仅是估算。 2)如果主线程休眠时间长了,…...

盘点六款颇具潜力的伪原创AI工具
写作作为信息传递的主要媒介,在庞大的信息海洋中,为了在激烈的竞争中脱颖而出,伪原创AI工具成为越来越多写手的神秘利器。在本文中,我们将深入盘点六款颇具潜力的伪原创AI工具,为你揭开它们神秘的面纱。 1. 文心一言 …...
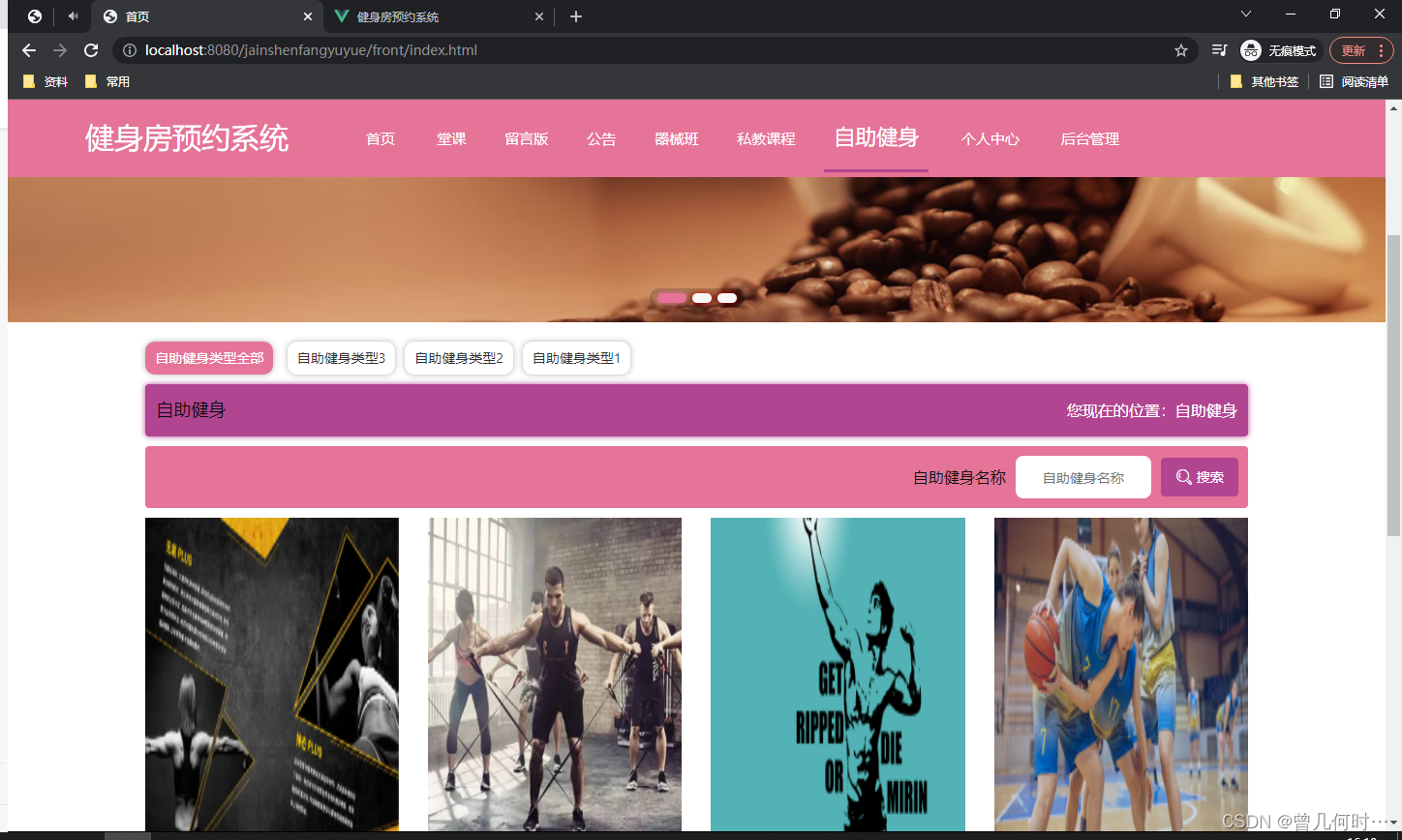
基于SSM的健身房预约系统设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...
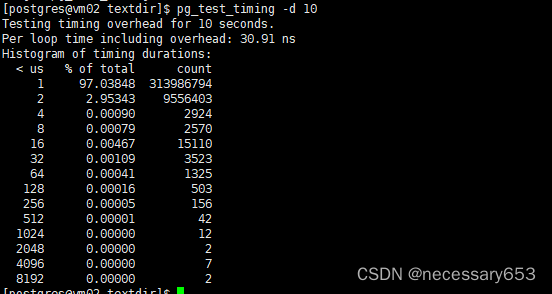
postgresql自带指令命令系列二
简介 在安装postgresql数据库的时候会需要设置一个关于postgresql数据库的PATH变量 export PATH/home/postgres/pg/bin:$PATH,该变量会指向postgresql安装路径下的bin目录。这个安装目录和我们在进行编译的时候./configure --prefix [指定安装目录] 中的prefix参…...
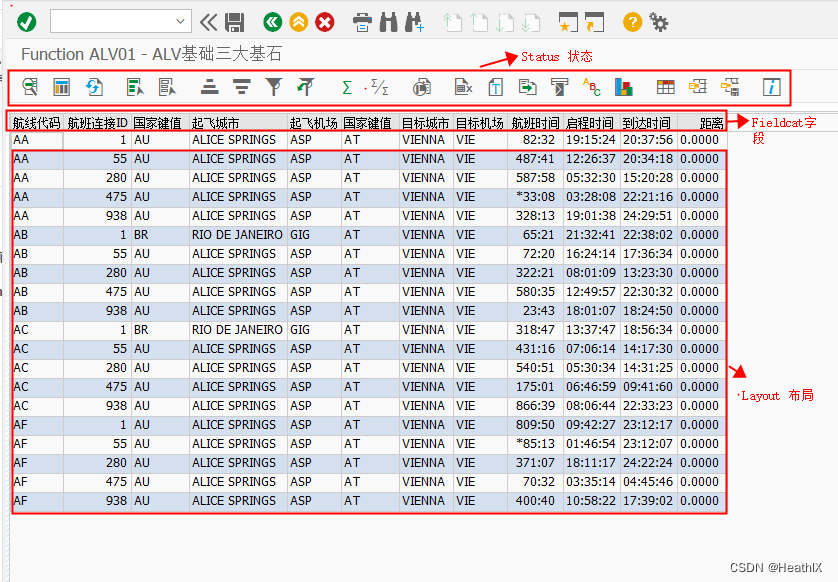
ABAP - Function ALV 02 简单开发一个Function ALV
了解Function ALV: https://blog.csdn.net/HeathlX/article/details/134879766?spm1001.2014.3001.5501程序开发步骤:① TCODE:SE38创建程序 ② 编写程序 DATA gt_spfli TYPE TABLE OF spfli.** Layout 变量定义 (固定使用 直接粘贴复制即可) DATA gs…...

IDEA启动失败报错解决思路
IDEA启动失败报错解决思路 背景:在IDEA里安装插件失败,重启后直接进不去了,然后分析问题解决问题的过程记录下来。方便下次遇到快速解决。也是一种解决问题的思路,分享出去。 启动报错信息 Internal error. Please refer to https…...
密码学学习笔记(二十三):哈希函数的安全性质:抗碰撞性,抗第一原象性和抗第二原象性
在密码学中,哈希函数是一种将任意长度的数据映射到固定长度输出的函数,这个输出通常称为哈希值。理想的哈希函数需要具备几个重要的安全性质,以确保数据的完整性和验证数据的来源。这些性质包括抗碰撞性、抗第一原象性和抗第二原象性。 抗碰…...

STM32-GPIO编程
一、GPIO 1.1 基本概念 GPIO(General-purpose input/output)通用输入输出接口 --GP 通用 --I input输入 --o output输出 通用输入输出接口GPIO是嵌入式系统、单片机开发过程中最常用的接口,用户可以通过编程灵活的对接口进行控制,…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
