力扣编程题算法初阶之双指针算法+代码分析
目录
第一题:复写零
第二题:快乐数:
第三题:盛水最多的容器
第四题:有效三角形的个数
第一题:复写零
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
 思路:
思路:
上期介绍到双指针,这次来用双指针实际操作。第一种从前往后复写,会导致为复写的数字被覆盖,因此选择从后往前复写,那么先找到复写的最后一个元素,再从后往前复写即可。
步骤
1.初始化指针
2.找复写
3.处理边界问题
4.开始复写
class Solution {
public:void duplicateZeros(vector<int>& arr) {int cur = 0, dest = -1, n = arr.size();
while (cur < n)
{if (arr[cur]) dest++;//说明不用复写else dest += 2;if (dest >= n - 1)break;cur++;
}
//出来的时候cur就是莫位置
//处理边界
if (dest == n)
{arr[n - 1] = 0;cur--; dest -= 2;
}
//从后往前面复写
while (cur >= 0)
{if (arr[cur])//非0arr[dest--] = arr[cur--];else//为0{arr[dest--] = 0;arr[dest--] = 0;cur--;}
}}
};第二题:快乐数:
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台

思路:
这题通过在纸上演算可以发现,给定一个数他按照快乐数的定义,要么演变到1,要么将会重复他在演变过程中的一个数字,具体大家可以在纸上推算一遍
即
:
class Solution
{
public:int bitSum(int n)int sum = 0;while (n){int t = n % 10;sum += t * t;n /= 10;}bool isHappy(int n){int slow = n, fast = bitSum(n);while (slow != fast){slow = bitSum(slow);fast = bitSum(bitSum(fast));}return slow == 1;}
};第三题:盛水最多的容器
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
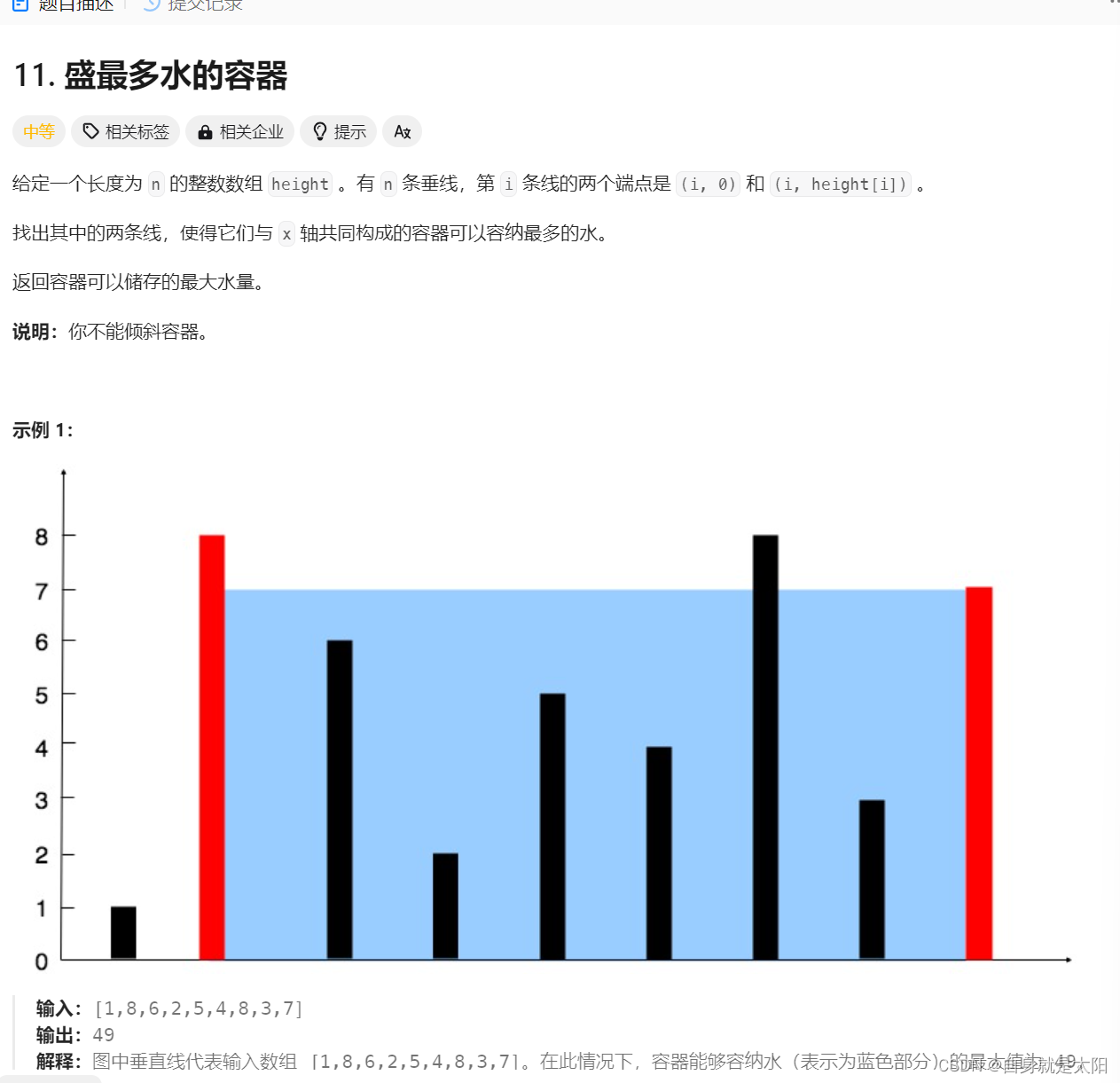 思路:
思路:
第一想法就是暴力枚举
s=h(高)*w(宽度)
即弄两个for循环,依次求出面积,再比较最大值,这样时间复杂度为n的平方会超时,因此
第二种就是双指针,观察发现,面积的高是由左右两边的低边界为准。就以上图为例,高是由右边那条高决定,左边高往右移动由于w一定减小,h要么减小要么不变,那么面积一定减小,所以我们就从两个边界开始来移动,记录每一次的面积,返回最大即可
注意,每次移动的是那个h小的,因为大h移动,s要么减少要么不变,而我们求的是最大的。
第一种:暴力求解
class Solution {
public:int maxArea(vector<int>& height) {int n = height.size();int ret = 0;// 两层 for 枚举出所有可能出现的情况for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {// 计算容积,找出最⼤的那⼀个ret = max(ret, min(height[i], height[j]) * (j - i));}}return ret;}
};第二种:
对撞指针:
class Solution
{
public:int maxArea(vector<int>& height){int left = 0, right = height.size() - 1, ret = 0;while (left < right){int v = min(height[left], height[right]) * (right - left);ret = max(ret, v);// 移动指针if (height[left] < height[right]) left++;else right--;}return ret;}
};
第四题:有效三角形的个数
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
 思路:
思路:
在判断一个三角形时,如果对于一对升序数组a,b,c
如果a+b>c那么即可构成三角形,不需要判断三次
原因,如果上述条件成立那么,b+c>a,a+c>b一定成立,因为c是最大的数
第一思路就是暴力求解,先把给定数组排序,然后从第一个元素开始遍历,用三个for循环实现,但是时间复杂度较大,运行会超时
class Solution {
public:int triangleNumber(vector<int>& nums) {// 1. 排序sort(nums.begin(), nums.end());int n = nums.size(), ret = 0;// 2. 从⼩到⼤枚举所有的三元组for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {for (int k = j + 1; k < n; k++) {// 当最⼩的两个边之和⼤于第三边的时候,统计答案if (nums[i] + nums[j] > nums[k])ret++;}}}return ret;}
};应次这里换一种高效方法就是用双指针来实现,因为已经排完升序,依据暴力解法,可以先固定一条最长边,然后找出比这条边小的二元组,让着个二元组的和大于最长边,即可利用对撞指针来实现。
class Solution
{
public:int triangleNumber(vector<int>& nums){// 1. 优化sort(nums.begin(), nums.end());// 2. 利⽤双指针解决问题int ret = 0, n = nums.size();for (int i = n - 1; i >= 2; i--) // 先固定最⼤的数{// 利⽤双指针快速统计符合要求的三元组的个数int left = 0, right = i - 1;while (left < right){if (nums[left] + nums[right] > nums[i]){ret += right - left;right--;}else{left++;}}}return ret;}
};
相关文章:

力扣编程题算法初阶之双指针算法+代码分析
目录 第一题:复写零 第二题:快乐数: 第三题:盛水最多的容器 第四题:有效三角形的个数 第一题:复写零 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 思路: 上期…...
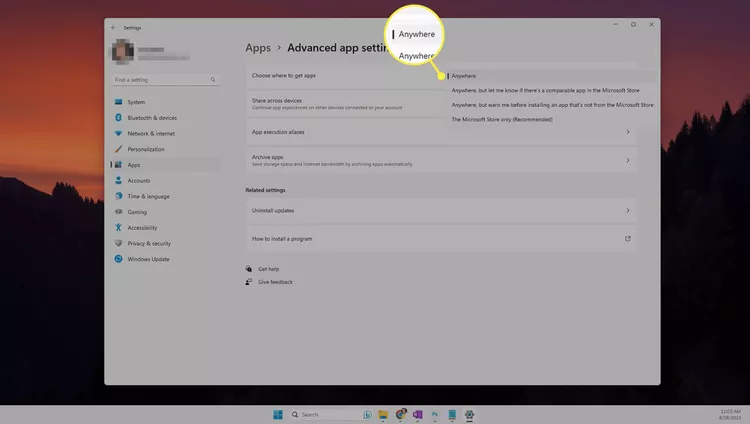
实现安装“自由化”!在Windows 11中如何绕过“您尝试安装的应用程序未通过微软验证”
这篇文章描述了如果你不能安装应用程序,而是当你在Windows 11中看到消息“您尝试安装的应用程序未通过微软验证”时该怎么办。完成这些步骤将取消你安装的应用程序必须经过Microsoft验证的要求。 使用设置应用程序 “设置”应用程序提供了绕过此警告消息的最简单方法,以便你…...
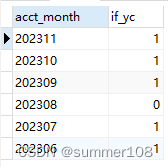
【mysql】下一行减去上一行数据、自增序列场景应用
背景 想获取if_yc为1连续账期数据 思路 获取所有if_yc为1的账期数据下一行减去上一行账期,如果为1则为连续,不等于1就为断档获取不等于1的最小账期,就是离当前账期最近连续账期 代码 以下为mysql语法: select acct_month f…...
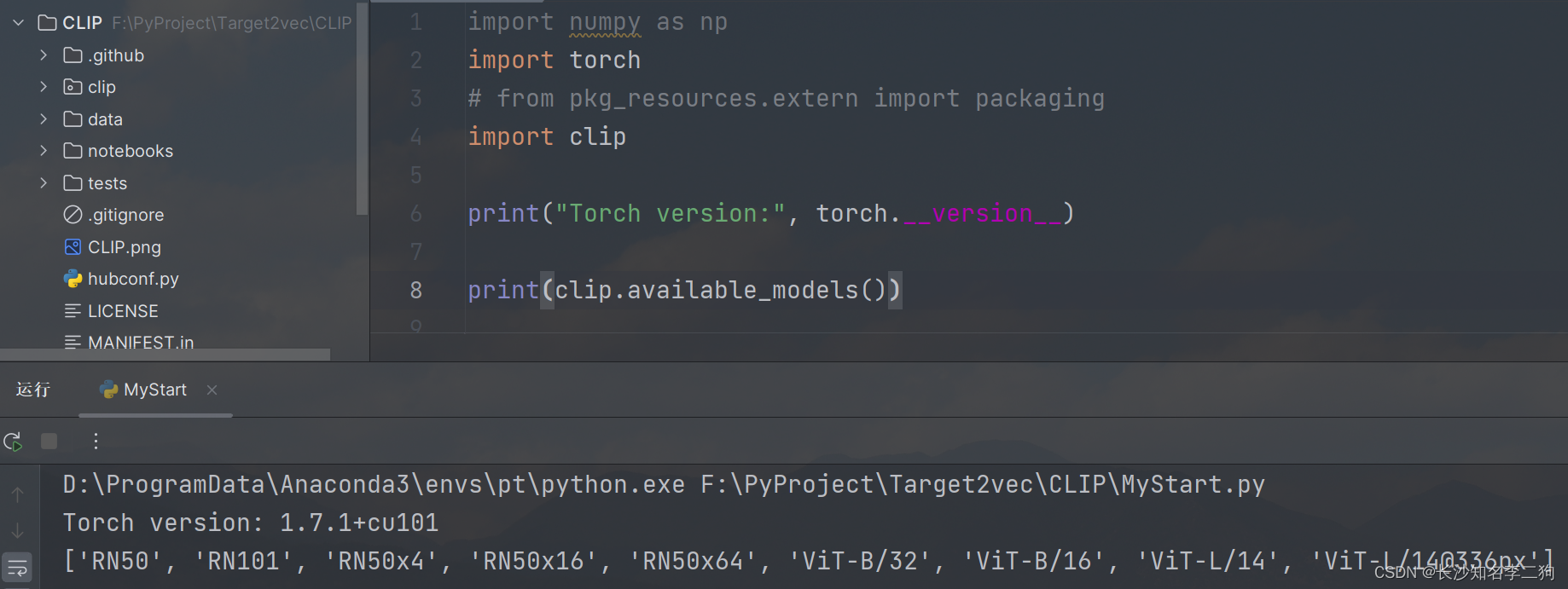
CLIP在Github上的使用教程
CLIP的github链接:https://github.com/openai/CLIP CLIP Blog,Paper,Model Card,Colab CLIP(对比语言-图像预训练)是一个在各种(图像、文本)对上进行训练的神经网络。可以用自然语…...
入职字节外包一个月,我离职了。。。
有一种打工人的羡慕,叫做“大厂”。 真是年少不知大厂香,错把青春插稻秧。 但是,在深圳有一群比大厂员工更庞大的群体,他们顶着大厂的“名”,做着大厂的工作,还可以享受大厂的伙食,却没有大厂…...

SpringBoot的web开发
与其明天开始,不如现在行动! 文章目录 web开发1 web场景1.1 自动配置1.2 默认效果 💎总结 web开发 SpringBoot的web开发能力是由SpringMVC提供的 1 web场景 1.1 自动配置 整合web场景 <dependency><groupId>org.springframewo…...

传染病传播速度
题干 R0值是基本传染数的简称,指的是在没有采取任何干预措施的情况下,平均每位感染者在传染期内使易感者个体致病的数量。数字越大说明传播能力越强,控制难度越大。一个人传染的人的数量可以用幂运算来计算。假设奥密克戎的R0为10࿰…...
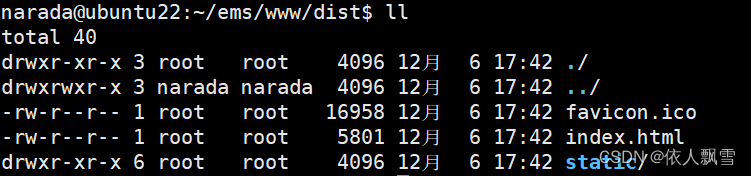
前端打包环境配置步骤
获取node安装包并解压 获取node安装包 wget https://npmmirror.com/mirrors/node/v16.14.0/node-v16.14.0-linux-x64.tar.xz 解压 tar -xvf node-v16.14.0-linux-x64.tar.xz 创建软链接 sudo ln -s 此文件夹的绝对路径/bin/node /usr/local/bin/node,具体执行如下…...
、内部样式表(<style>)、外部样式表(<link>、@import))
css的4种引入方式--内联样式(标签内style)、内部样式表(<style>)、外部样式表(<link>、@import)
1.内联样式(Inline Styles):可以直接在HTML元素的style属性中定义CSS样式。 例如: <p style"color: red; font-size: 16px;">这是一段红色的文本</p>内联样式适用于对单个元素应用特定的样式,…...

GPT-4 变懒了?官方回复
你是否注意到,最近使用 ChatGPT 的时候,当你向它提出一些问题,却得到的回应似乎变得简短而敷衍了?对于这一现象,ChatGPT 官方给出了回应。 译文:我们听到了你们所有关于 GPT4 变得更懒的反馈!我…...

编译器和 IR:LLVM IR、SPIR-V 和 MLIR
编译器通常是各种开发工具链中的关键组件,可提高开发人员的工作效率。编译器通常用作独立的黑匣子,它使用高级源程序并生成语义上等效的低级源程序。不过,它仍然是内部结构倾向的;内部之间流动的内容就称为中间表示 (IR࿰…...

蓝牙物联网对接技术难点有哪些?
#物联网# 蓝牙物联网对接技术难点主要包括以下几个方面: 1、设备兼容性:蓝牙技术有多种版本和规格,如蓝牙4.0、蓝牙5.0等,不同版本之间的兼容性可能存在问题。同时,不同厂商生产的蓝牙设备也可能存在兼容性问题。 2、…...

漫谈Uniapp App热更新包-Jenkins CI/CD打包工具链的搭建
零、写在前面 HBuilderX是DCloud旗下的IDE产品,目前只提供了Windows和Mac版本使用。本项目组在开发阶段经常需要向测试环境提交热更新包,使用Jenkins进行CD是非常有必要的一步。尽管HBuilderX提供了CLI,但Jenkins服务通常都是搭建在Linux环境…...
Axure简单安装与入门
目录 一.Axure简介 二.应用场景 三.安装与汉化 3.1.安装 3.2.汉化 四. 入门 4.1.复制、剪切及粘贴区域 4.2.选择模式 4.3. 插入形状 4.4.预览、共享 感谢大家观看!希望能帮到你哦!!! 一.Axure简介 Axure RP是一款专业的原型…...
———前端开发与后端开发有什么区别)
前端知识笔记(四十五)———前端开发与后端开发有什么区别
前端开发和后端开发是Web开发中的两个关键领域,它们负责不同的任务和功能。下面是前端开发和后端开发之间的主要区别: 前端开发: 用户界面:前端开发主要关注用户界面的开发,包括网页的布局、样式、交互等方面。前端技…...
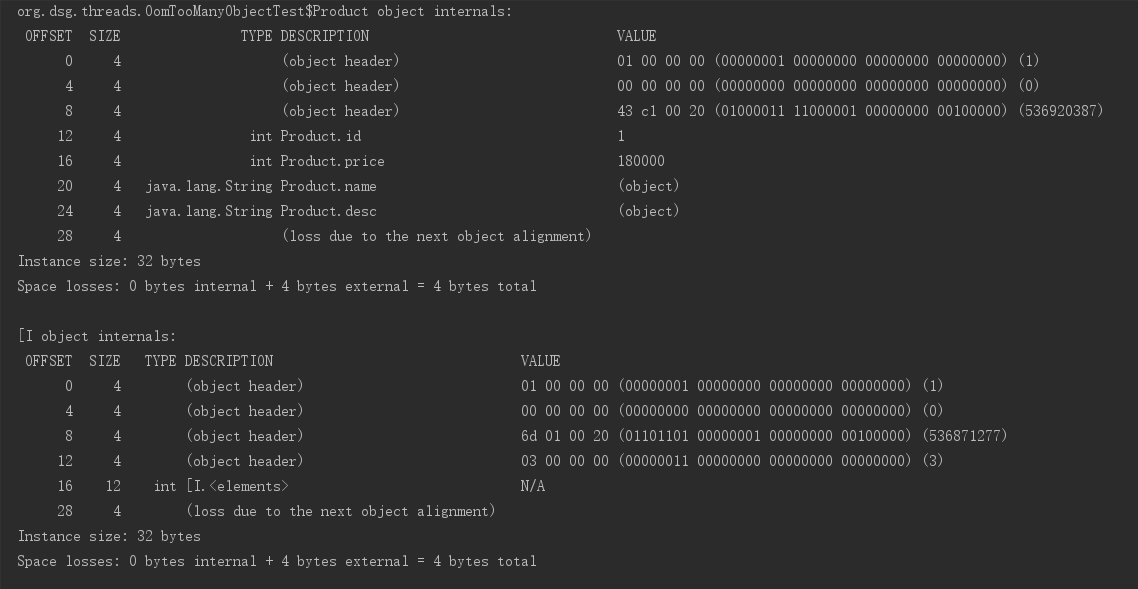
Jol-分析Java对象的内存布局
Jol-分析Java对象的内存布局 Open JDK提供的JOL(Java Object Layout)工具为我们方便分析、了解一个Java对象在内存当中的具体布局情况。本文实验环境为64位HotSpot虚拟机。 Java对象的内存布局 Java的实例对象、数组对象在内存中的组成包括:对象头、实例数据和内存…...

基于sfunction builder的c-sfunction编写及案例测试分析
目录 前言 1.前期准备工作及文件说明 1.1前期准备工作 1.2 文件说明 1.3 编译方式...
知识点总结)
【Java期末复习资料】(1)知识点总结
本文章主要是知识点,后续会出模拟卷 以下是选择、填空可能考的知识点,多看几遍,混个眼熟 面向对象程序设计的基本特征是:抽象、封装、继承、多态(后三个是三大特性)Java源文件的扩缀名是.java编译Java App…...

进程、容器与虚拟机的区别
进程、容器与虚拟机 参考:关于进程、容器与虚拟机的区别,你想知道的都在这! 进程、容器与虚拟机的结构图 进程 介绍 进程是一个正在运行的程序,它是一个个可执行文件的实例。当一个可执行文件从硬盘加载到内存中的时候…...
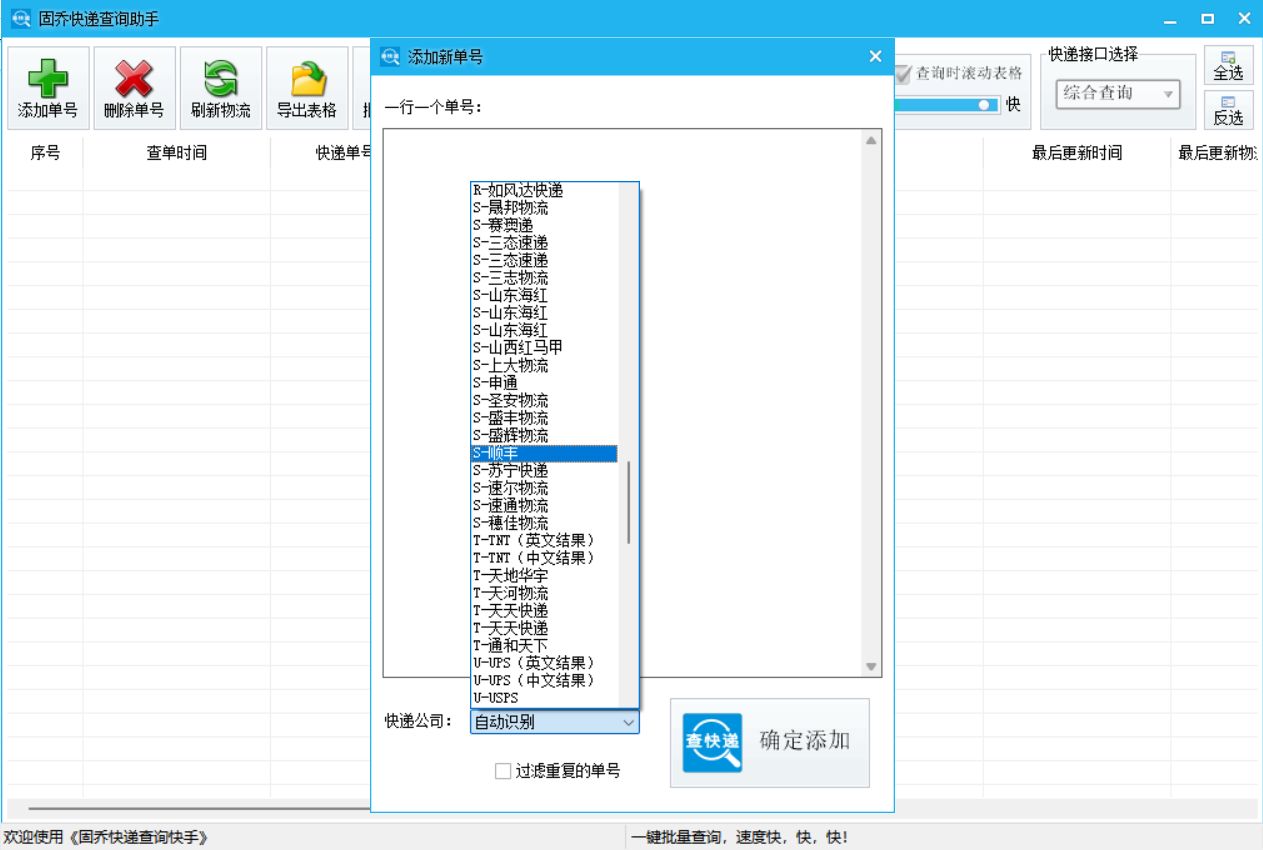
全网快递批量查询的得力助手
在当今社会,网络购物已经成为人们日常生活的重要组成部分。随着网购的普及,快递行业也迅速发展壮大。然而,这也带来了一系列问题:如何快速、准确地查询快递信息?如何批量查询多个快递?今天,我们…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...
