【算法专题】分治 - 快速排序
分治 - 快速排序
- 分治 - 快速排序
- 1. 颜色分类
- 2. 排序数组(快速排序)
- 3. 数组中的第K个最大元素
- 4. 库存管理Ⅲ
- 5. 排序数组(归并排序)
- 6. 交易逆序对的总数
- 7. 计算右侧小于当前元素的个数
- 8. 翻转对
分治 - 快速排序
1. 颜色分类
做题链接 -> Leetcode -75.颜色分类
题目:给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库内置的 sort 函数的情况下解决这个问题。
示例 1:
输入:nums = [2, 0, 2, 1, 1, 0]
输出:[0, 0, 1, 1, 2, 2]
示例 2:
输入:nums = [2, 0, 1]
输出:[0, 1, 2]
提示:
n == nums.length
1 <= n <= 300
nums[i] 为 0、1 或 2
思路:快排思想,三指针法使数组分三块。类比数组分两块的算法思想,这里是将数组分成三块,那么我们可以再添加⼀个指针,实现数组分三块。
设数组大小为 n ,定义三个指针 left, cur, right :
- left :用来标记 0(红色) 序列的末尾,因此初始化为 -1 ;
- cur :用来扫描数组,初始化为 0 ;
- right :用来标记 2(蓝色) 序列的起始位置,因此初始化为 n 。
在 cur 往后扫描的过程中,保证:
- [0, left] 内的元素都是 0(红色) ;
- [left + 1, cur - 1] 内的元素都是 1(白色) ;
- [cur, right - 1] 内的元素是待定元素;
- [right, n] 内的元素都是 2(蓝色) .
代码如下:
class Solution {public:void sortColors(vector<int>& nums) {// 使用三指针将数组分为三块,最终分为以下三个模块:// [0, left] 表示 0(红色) 序列;// [left + 1, right - 1] 表示 1(白色) 序列;// [right, numsSize - 1] 表示 2(蓝色) 序列。 int cur = 0, left = -1, right = nums.size();while(cur < right){if(nums[cur] == 0) swap(nums[++left], nums[cur++]);else if(nums[cur] == 1) cur++;else swap(nums[--right], nums[cur]);}}};
2. 排序数组(快速排序)
做题链接 -> Leetcode -912.排序数组
题目:给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5, 2, 3, 1]
输出:[1, 2, 3, 5]
示例 2:
输入:nums = [5, 1, 1, 2, 0, 0]
输出:[0, 0, 1, 1, 2, 5]
提示:
1 <= nums.length <= 5 * 10^4
5 * 10^4 <= nums[i] <= 5 * 10^4
由于思路比较明显,使用快速选择算法,递归处理选取一个基准值 key 将数组分为三块,下面直接看代码:
class Solution {public:vector<int> sortArray(vector<int>& nums) {// 种下一个随机数种子srand(time(nullptr));// 快速选择算法,将数组划分为三个区间my_qsort(nums, 0, nums.size() - 1);return nums;}void my_qsort(vector<int>& nums, int l, int r){if(l >= r) return;// 将数组分三块int key = getRandom(nums, l, r);int i = l, left = l - 1, right = r + 1;while(i < right){if(nums[i] > key) swap(nums[i], nums[--right]);else if(nums[i] == key) ++i;else swap(nums[++left], nums[i++]);}// [l, left] [left + 1, right - 1] [right, r]my_qsort(nums, l, left);my_qsort(nums, right, r);}// 获取数组中随机一个数// 让随机数 % 上区间大小,然后加上区间的左边界int getRandom(vector<int>& nums, int left, int right){return nums[rand() % (right - left + 1) + left];}};
3. 数组中的第K个最大元素
题目链接 -> Leetcode -215.数组中的第K个最大元素
Leetcode -215.数组中的第K个最大元素
题目:给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入: [3, 2, 1, 5, 6, 4] , k = 2
输出 : 5
示例 2 :
输入 : [3, 2, 3, 1, 2, 4, 5, 5, 6] , k = 4
输出 : 4
提示:
- 1 <= k <= nums.length <= 10^5
- 10^4 <= nums[i] <= 10^4
思路是使用快排思想,将数组分为三块,然后分三种情况讨论,具体思路参考代码解析;
代码如下:
class Solution {public:int findKthLargest(vector<int>& nums, int k){srand(time(nullptr));return FindMaxTopk(nums, 0, nums.size() - 1, k);}int FindMaxTopk(vector<int>& nums, int l, int r, int k){if (l == r) return nums[l];// 根据 key 将数组分为三块int key = getRandom(nums, l, r);int i = l, left = l - 1, right = r + 1;while (i < right){if (nums[i] < key) swap(nums[++left], nums[i++]);else if (nums[i] == key) i++;else swap(nums[--right], nums[i]);}// [l, left] [left + 1, right - 1] [right, r]int part2 = right - left - 1, part3 = r - right + 1;// 分情况讨论// 情况1、区间3的个数大于等于k,那么目标值一定在区间3if (part3 >= k) return FindMaxTopk(nums, right, r, k);// 情况2、区间2+区间3的个数大于等于k,目标值一定在区间2,即一定是 keyelse if (part2 + part3 >= k) return key;// 情况3、如果不满足上面情况,则目标值一定在区间1else return FindMaxTopk(nums, l, left, k - part2 - part3);}// 获取数组内的一个随机值int getRandom(vector<int>& nums, int left, int right){return nums[rand() % (right - left + 1) + left];}};
4. 库存管理Ⅲ
题目链接 -> Leetcode -LCR 159.库存管理Ⅲ
Leetcode -LCR 159.库存管理Ⅲ
题目:仓库管理员以数组 stock 形式记录商品库存表,其中 stock[i] 表示对应商品库存余量。
请返回库存余量最少的 cnt 个商品余量,返回 顺序不限。
示例 1:
输入:stock = [2, 5, 7, 4], cnt = 1
输出:[2]
示例 2:
输入:stock = [0, 2, 3, 6], cnt = 2
输出:[0, 2] 或[2, 0]
提示:
0 <= cnt <= stock.length <= 10000
0 <= stock[i] <= 10000
思路:与上题思路类似;在快排中,当我们把数组「分成三块」之后: [l, left] [left + 1, right - 1] [right, r] ,我们可以通过计算每一个区间内元素的「个数」,进而推断出最小的 k 个数在哪些区间里面。那么我们可以直接去「相应的区间」继续划分数组即可。
代码如下:
class Solution {public:void my_qsort(vector<int>& arr, int l, int r, int k){if(l >= r) return;// 根据 key 值分区间int key = getRandom(arr, l, r);int i = l, left = l - 1, right = r + 1;while(i < right){if(arr[i] < key) swap(arr[++left], arr[i++]);else if(arr[i] == key) i++;else swap(arr[--right], arr[i]);}// 根据元素个数分情况讨论// [l, left] [left + 1][right - 1] [right, r]int part1 = left - l + 1, part2 = right - left - 1;if(part1 >= k) my_qsort(arr, l, left, k);else if(part1 + part2 >= k) return;else my_qsort(arr, right, r, k - part1 - part2);}// 选取基准值int getRandom(vector<int>& arr, int left, int right){return arr[rand() % (right - left + 1) + left];}vector<int> inventoryManagement(vector<int>& stock, int cnt) {srand(time(nullptr));// 快速选择算法,将数组分为三个区间,选择基准值key,比key小的元素全扔到左边my_qsort(stock, 0, stock.size() - 1, cnt);return vector<int>(stock.begin(), stock.begin() + cnt);}};
5. 排序数组(归并排序)
题目链接 -> Leetcode -912.排序数组(归并排序)
Leetcode -912.排序数组(归并排序)
题目:给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5, 2, 3, 1]
输出:[1, 2, 3, 5]
示例 2:
输入:nums = [5, 1, 1, 2, 0, 0]
输出:[0, 0, 1, 1, 2, 5]
提示:
- 1 <= nums.length <= 5 * 10^4
- 5 * 10^4 <= nums[i] <= 5 * 10^4
思路:归并排序的流程充分的体现了「分而治之」的思想,大体过程分为两步:
- 分:将数组一分为二为两部分,一直分解到数组的长度为 1 ,使整个数组的排序过程被分为「左半部分排序」 + 「右半部分排序」;
- 治:将两个较短的「有序数组合并成⼀个长的有序数组」,一直合并到最初的长度
代码如下:
class Solution{vector<int> tmp;public:vector<int> sortArray(vector<int>& nums){tmp.resize(nums.size());mergeSort(nums, 0, nums.size() - 1);return nums;}void mergeSort(vector<int>& nums, int left, int right){if (left >= right) return;int mid = left + (right - left) / 2;// [left, mid] [mid + 1, right]mergeSort(nums, left, mid);mergeSort(nums, mid + 1, right);// 合并两个区间// vector<int> tmp(right - left + 1); // 可以在全局定义,提高效率int i = 0, cur1 = left, cur2 = mid + 1;while (cur1 <= mid && cur2 <= right)tmp[i++] = nums[cur1] <= nums[cur2] ? nums[cur1++] : nums[cur2++];while (cur1 <= mid) tmp[i++] = nums[cur1++];while (cur2 <= right) tmp[i++] = nums[cur2++];// 更新原数组for (int i = left; i <= right; i++)nums[i] = tmp[i - left];}};
6. 交易逆序对的总数
题目链接 -> Leetcode -LCR 170.交易逆序对的总数
Leetcode -LCR 170.交易逆序对的总数
题目:在股票交易中,如果前一天的股价高于后一天的股价,则可以认为存在一个「交易逆序对」。请设计一个程序,输入一段时间内的股票交易记录 record,返回其中存在的「交易逆序对」总数。
示例 1:
输入:record = [9, 7, 5, 4, 6]
输出:8
解释:交易中的逆序对为(9, 7), (9, 5), (9, 4), (9, 6), (7, 5), (7, 4), (7, 6), (5, 4)。
限制:
- 0 <= record.length <= 50000
思路:用归并排序求逆序数,主要就是在归并排序的合并过程中统计出逆序对的数量,也就是在合并两个有序序列的过程中,能够快速求出逆序对的数量。
1. 为什么可以利用归并排序?
如果我们将数组从中间划分成两个部分,那么我们可以将逆序对产生的方式划分成三组:
- 逆序对中两个元素:全部从左数组中选择
- 逆序对中两个元素:全部从右数组中选择
- 逆序对中两个元素:一个选左数组另一个选右数组
根据排列组合的分类相加原理,三种情况下产生的逆序对的总和,正好等于总的逆序对数量。
而这个思路正好匹配归并排序的过程:
- 先排序左数组;
- 再排序右数组;
- 左数组和右数组合⼆为一;
因此,我们可以利用归并排序的过程,先求出左半数组中逆序对的数量,再求出右半数组中逆序对的数量,最后求出一个选择左边,另一个选择右边情况下逆序对的数量,三者相加即可。
2. 为什么要这么做?
在归并排序合并的过程中,我们得到的是两个有序的数组。我们是可以利用数组的有序性,快速统计出逆序对的数量,而不是将所有情况都枚举出来。
最核心的问题,如何在合并两个有序数组的过程中,统计出逆序对的数量?合并两个有序序列时求逆序对的方法有两种:
- 快速统计出某个数前面有多少个数比它大;
- 快速统计出某个数后面有多少个数比它小;
代码如下:
class Solution{vector<int> tmp;public:int reversePairs(vector<int>& nums){tmp.resize(nums.size());return mergeSort(nums, 0, nums.size() - 1);}int mergeSort(vector<int>& nums, int left, int right){if (left >= right) return 0;// [left, mid] [mid + 1, right]int mid = left + (right - left) / 2;// 先统计两个区间各自的逆序对个数 + 排序int ret = 0;ret += mergeSort(nums, left, mid);ret += mergeSort(nums, mid + 1, right);// 两个区间每个区间选一个进行比较,因为比较时区间已经排序好,所以当cur1中出现第一次比cur2大的数时,cur1 后面的数都可以全部统计int cur1 = left, cur2 = mid + 1, i = 0;while (cur1 <= mid && cur2 <= right){if (nums[cur1] > nums[cur2]) ret += mid - cur1 + 1;tmp[i++] = nums[cur1] <= nums[cur2] ? nums[cur1++] : nums[cur2++];}// 处理细节,还没结束的指针后的数全放入tmp中while (cur1 <= mid) tmp[i++] = nums[cur1++];while (cur2 <= right) tmp[i++] = nums[cur2++];// 拷贝回原数组for (int i = left; i <= right; i++) nums[i] = tmp[i - left];return ret;}};
7. 计算右侧小于当前元素的个数
题目链接 -> Leetcode -315.计算右侧小于当前元素的个数
Leetcode -315.计算右侧小于当前元素的个数
题目:给你一个整数数组 nums ,按要求返回一个新数组 counts 。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例 1:
输入:nums = [5, 2, 6, 1]
输出:[2, 1, 1, 0]
解释:
5 的右侧有 2 个更小的元素(2 和 1)
2 的右侧仅有 1 个更小的元素(1)
6 的右侧有 1 个更小的元素(1)
1 的右侧有 0 个更小的元素
示例 2:
输入:nums = [-1]
输出:[0]
示例 3:
输入:nums = [-1, -1]
输出:[0, 0]
提示:
- 1 <= nums.length <= 10^5
- 10^4 <= nums[i] <= 10^4
思路:这一道题的解法与上一题的解法是类似的,但是这一道题要求的不是求总的个数,而是要返回一个数组,记录每一个元素的右边有多少个元素比自己小。
但是在我们归并排序的过程中,元素的下标是会跟着变化的,因此我们需要一个辅助数组,来将数组元素和对应的下标绑定在一起归并,也就是再归并元素的时候,顺势将下标也转移到对应的位置上。
代码如下:
class Solution {// 将原数组的元素和下标绑定在一起,元素顺序改变时,对应的下标也跟着改变vector<int> tmpElement, tmpIndex;vector<int> index;vector<int> ret;public:vector<int> countSmaller(vector<int>& nums) {ret.resize(nums.size());index.resize(nums.size());// 初始化下标for(int i = 0; i < nums.size(); i++)index[i] = i;tmpElement.resize(nums.size());tmpIndex.resize(nums.size());mergeSort(nums, 0, nums.size() - 1);return ret;}void mergeSort(vector<int>& nums, int left, int right){if(left >= right) return;int mid = left + (right - left) / 2;// [left, mid] [mid + 1, right]mergeSort(nums, left, mid);mergeSort(nums, mid + 1, right);int cur1 = left, cur2 = mid + 1, i = 0;while(cur1 <= mid && cur2 <= right){// index[cur1] 存的是 nums[cur1] 这个元素的原始下标if(nums[cur1] > nums[cur2]) ret[index[cur1]] += right - cur2 + 1;// 同步更新下标和元素tmpIndex[i] = nums[cur1] > nums[cur2]? index[cur1] : index[cur2];tmpElement[i++] = nums[cur1] > nums[cur2]? nums[cur1++] : nums[cur2++];}while(cur1 <= mid){tmpIndex[i] = index[cur1];tmpElement[i++] = nums[cur1++];}while(cur2 <= right){tmpIndex[i] = index[cur2];tmpElement[i++] = nums[cur2++];}// 同步拷贝下标和元素for(int j = left; j <= right; j++){index[j] = tmpIndex[j - left];nums[j] = tmpElement[j - left];}}};
8. 翻转对
题目链接 -> Leetcode -493.翻转对
Leetcode -493.翻转对
题目:给定一个数组 nums ,如果 i < j 且 nums[i] > 2 * nums[j] 我们就将(i, j) 称作一个重要翻转对。
你需要返回给定数组中的重要翻转对的数量。
示例 1:
输入: [1, 3, 2, 3, 1]
输出 : 2
示例 2 :
输入 : [2, 4, 3, 5, 1]
输出 : 3
注意 :
给定数组的长度不会超过50000。
输入数组中的所有数字都在32位整数的表示范围内。
思路:翻转对和逆序对的定义大同小异,逆序对是前面的数要大于后面的数。而翻转对是前面的⼀个数要大于后面某个数的两倍。因此,我们依旧可以用归并排序的思想来解决这个问题。
大思路与求逆序对的思路一样,就是利用归并排序的思想,将求整个数组的翻转对的数量,转换成三部分:左半区间翻转对的数量,右半区间翻转对的数量,一左一右选择时翻转对的数量。重点就是在合并区间过程中,如何计算出翻转对的数量。
例如 left = [4, 5, 6] right = [3, 4, 5] 时,如果是归并排序的话,我们需要计算 left 数组中有多少个能与 3 组成翻转对。但是我们要遍历到最后⼀个元素 6 才能确定,时间复杂度较高。因此我们需要在归并排序之前完成翻转对的统计。
下面以⼀个示例来模仿两个有序序列如何快速求出翻转对的过程:假定已经有两个已经有序的序列 left = [4, 5, 6] right = [1, 2, 3] ;用两个指针 cur1 和 cur2 遍历两个数组
- 对于任意给定的 left[cur1] 而言,我们不断地向右移动 cur2,直到 left[cur1] <= 2 * right[cur2]。此时对于 right 数组而言,cur2 之前的元素全部都可以与 left[cur1] 构成翻转对。
- 随后,我们再将 cur1 向右移动⼀个单位,此时 cur2 指针并不需要回退(因为 left 数组是升序的)依旧往右移动直到 left[cur1] <= 2 * right[cur2]。不断重复这样的过程,就能够求出所有左右端点分别位于两个子数组的翻转对数目。
由于两个指针最后都是不回退的的扫描到数组的结尾,因此两个有序序列求出翻转对的时间复杂度是 O(N).
综上所述,我们可以利用归并排序的过程,将求一个数组的翻转对转换成求左数组的翻转对数量 + 右数组中翻转对的数量 + 左右数组合并时翻转对的数量。
代码如下:
class Solution {vector<int> tmp;public:int reversePairs(vector<int>& nums) { tmp.resize(nums.size());return mergeSort(nums, 0, nums.size() - 1);}int mergeSort(vector<int>& nums, int left, int right){if(left >= right) return 0;// 1.根据中间元素划分区间int mid = left + (right - left) / 2;// 2. 先计算左右区间的翻转对// [left, mid] [mid + 1, right]int ret = 0;ret += mergeSort(nums, left, mid);ret += mergeSort(nums, mid + 1, right);// 3.先利用左右区间有序的性质计算翻转对的数量int cur1 = left, cur2 = mid + 1, i = 0;while(cur1 <= mid){while(cur2 <= right && nums[cur2] >= nums[cur1] / 2.0) cur2++;ret += right - cur2 + 1;cur1++;}// 4.合并归并区间cur1 = left, cur2 = mid + 1;while(cur1 <= mid && cur2 <= right)tmp[i++] = nums[cur2] > nums[cur1]? nums[cur2++] : nums[cur1++];while(cur1 <= mid) tmp[i++] = nums[cur1++];while(cur2 <= right) tmp[i++] = nums[cur2++];for(int j = left; j <= right; j++)nums[j] = tmp[j - left];return ret;}};
相关文章:

【算法专题】分治 - 快速排序
分治 - 快速排序 分治 - 快速排序1. 颜色分类2. 排序数组(快速排序)3. 数组中的第K个最大元素4. 库存管理Ⅲ5. 排序数组(归并排序)6. 交易逆序对的总数7. 计算右侧小于当前元素的个数8. 翻转对 分治 - 快速排序 1. 颜色分类 做题链接 -> Leetcode -75.颜色分类 题目&…...
UG NX二次开发(C#)-求曲线在某一点处的法矢和切矢
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1、前言2、在UG NX中创建一个曲线3、直接放代码4、测试案例1、前言 最近确实有点忙了,好久没更新博客了。今天恰好有时间,就更新下,还请家人们见谅。 今天我们讲一下如何获取一条曲线上某一条曲…...
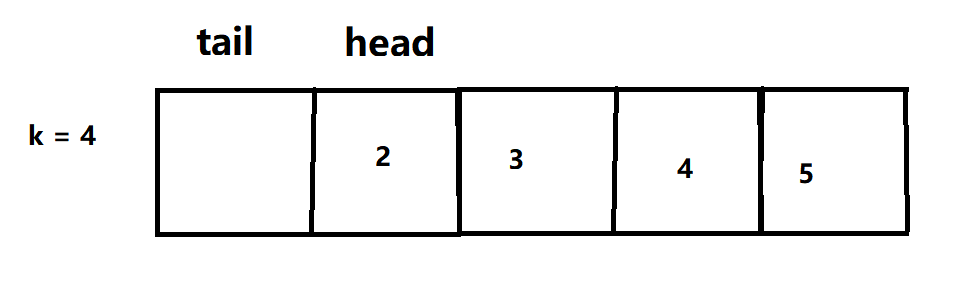
leetcode 622. 设计循环链表
这道题讲了两种方法,第一个代码是用数组实现的,第二个是用链表实现的,希望对你们有帮助 (最好在VS自己测试一遍,再放到 leetcode上哦) 下面的是主函数(作参考),静下心来…...
Linux:dockerfile编写搭建tomcat练习(9)
我使用的httpyum仓库 本地使用了5个文件,tomcat使用的官网解压直接用的包】 Dockerfile 主配置文件 基于centos基础镜像 jdk1.8.0_91 java环境 run.sh 启动脚本 centos.repo 仓库文件 tomcat 源码包 vim Dockerfile写入FROM centos MAINTAINER ta…...
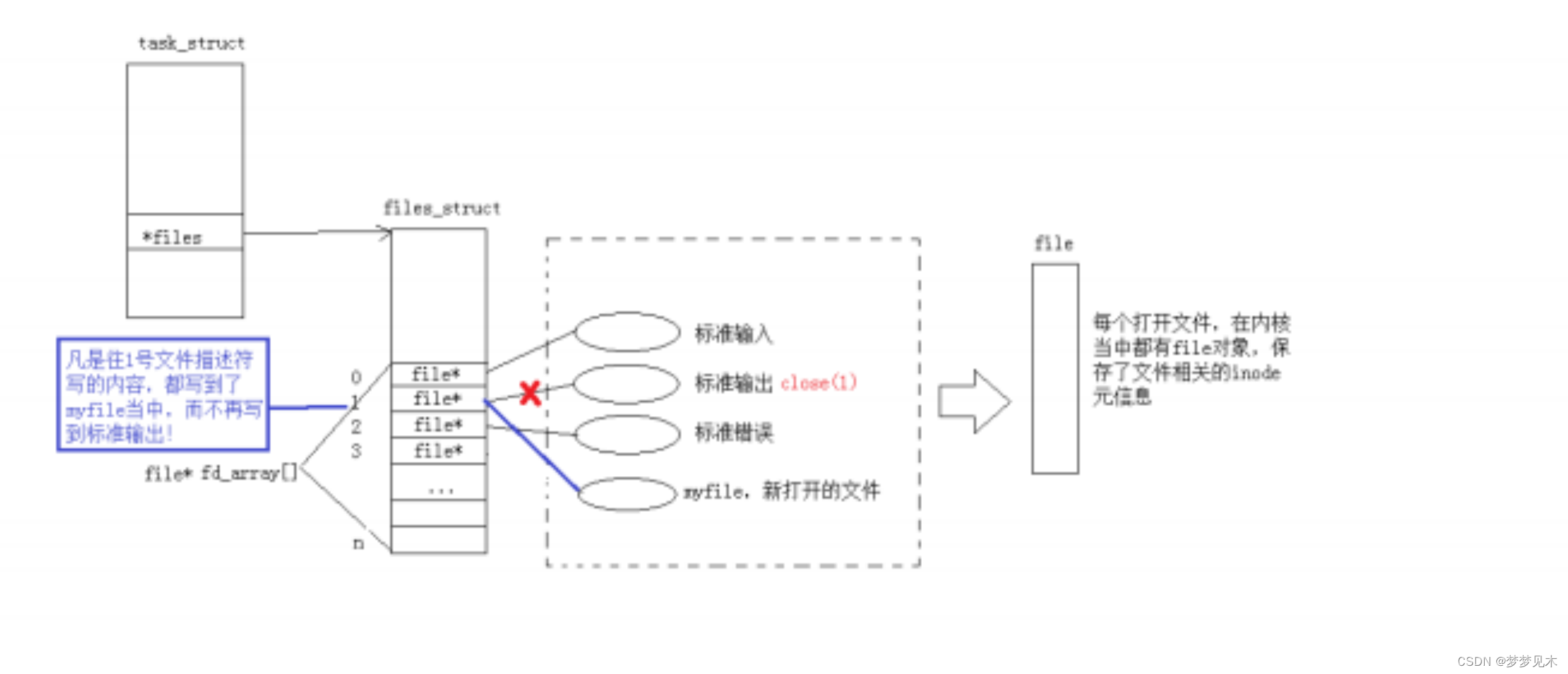
Linux 基础IO
文章目录 前言基础IO定义系统IO接口文件描述符重定向原理缓冲区刷新 前言 要知道每个函数/接口的全部参数和返回值建议去官网或者直接在Linux的man手册中查,这不是复制粘贴函数用法的文章。 C语言文件读写介绍链接 基础IO定义 IO是Input/Output的缩写,…...

uniapp 打开文件管理器上传(H5、微信小程序、android app三端)文件
H5跟安卓APP 手机打开的效果图: Vue页面: <template><view class"content"><button click"uploadFiles">点击上传</button></view> </template><script>export default {data() {return…...
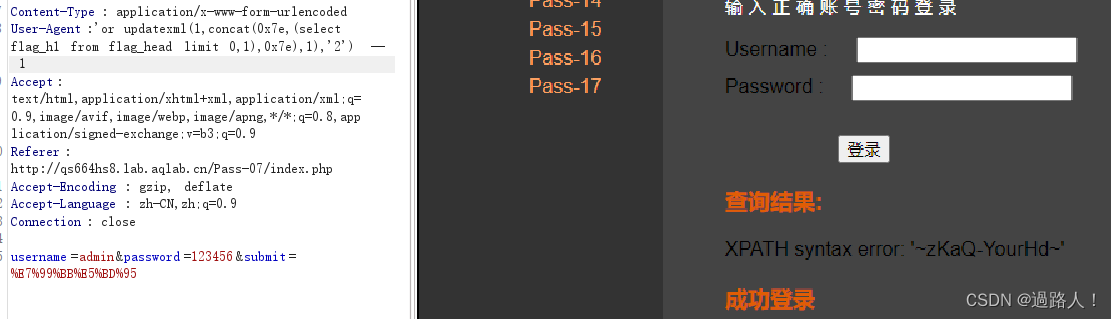
掌控安全 -- header注入
http header注入 该注入是指利用后端验证客户端口信息(比如常用的cookie验证)或者通过http header中获取客户端的一些信息(比如useragent用户代理等其他http header字段信息),因为这些信息是会重新返回拼接到后台中的&…...
如何激活Anconda Prompt虚拟环境)
windows批处理脚本(.bat)如何激活Anconda Prompt虚拟环境
通过call 来调用激活脚本, activate myenv指的是要激活的环境,若省略,则激活的是base环境。 call : 从另一个批处理程序调用一个批处理程序,而不停止父批处理程序。 call C:\ProgramData\Anaconda3\Scripts\activate.bat activate…...

扩散模型实战(十四):扩散模型生成音频
推荐阅读列表: 扩散模型实战(一):基本原理介绍 扩散模型实战(二):扩散模型的发展 扩散模型实战(三):扩散模型的应用 扩散模型实战(四ÿ…...

《微信小程序开发从入门到实战》学习四十七
4.4 云函数 4.4.5 云函数的定时触发 如果云函数需要定时执行,可以使用云函数定时触发器。配置了定时触发器,云函数会在相应时间点被自动触发。函数返回结果不会返回调用方 在需要添加触发器的云函数下新建文件config.json。格式如下: &quo…...

LeetCode刷题笔记之数组
一、二分查找 1. 704【二分查找】 题目: 给定一个 n 个元素 有序的(升序) 整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。代码:…...
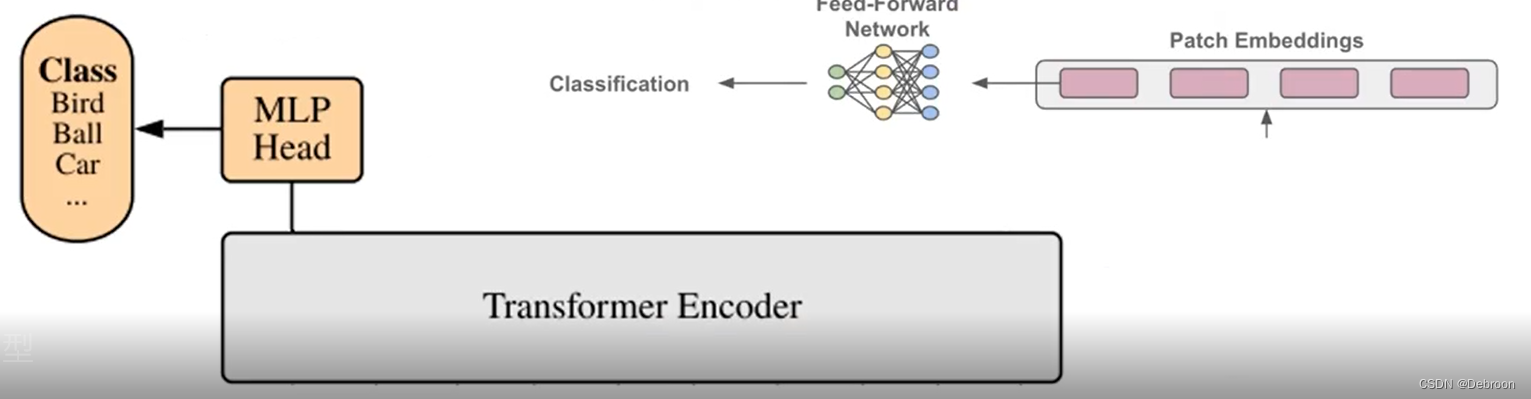
ViT:视觉 Transformer
ViT:视觉 Transformer 网络结构Transformer 编码器MLP 头CNN 和 Transformer 网络结构 Transformer 的优势:注意力机制相当于一个多标签检索系统,位置嵌入能知道每个单词的位置,而且适合并行。 尝试把 Transformer 迁移到视觉领…...
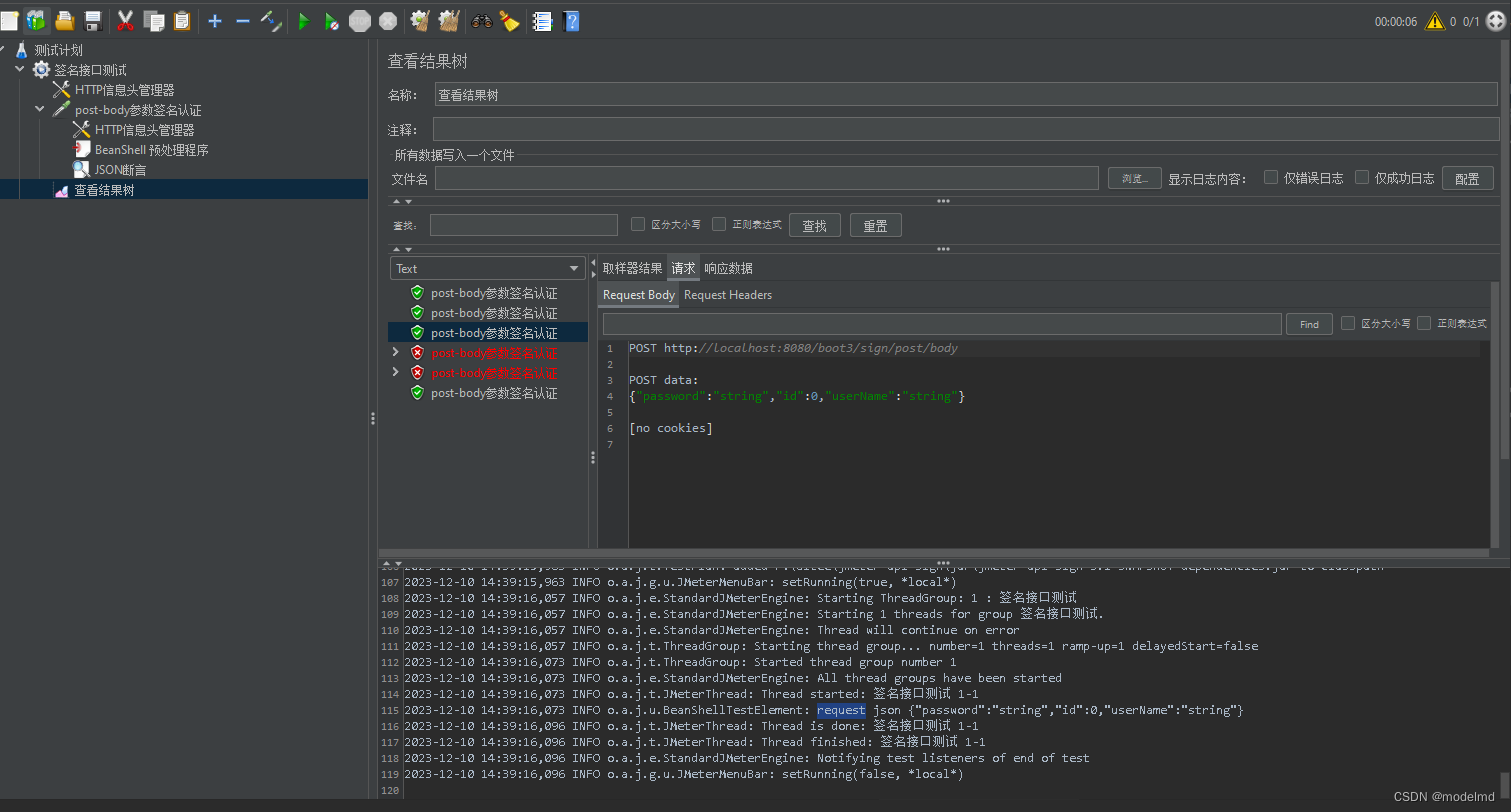
Jmeter 请求签名api接口-BeanShell
Jmeter 请求签名api接口-BeanShell 项目签名说明编译扩展jar包jmeter 使用 BeanShell 调用jar包中的签名方法 项目签名说明 有签名算法的api接口本地不好测试,使用BeanShell 扩展jar 包对参数进行签名,接口签名算法使用 sha512Hex 算法。签名的说明如下…...
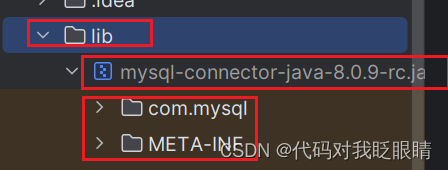
No suitable driver found for jdbc:mysql://localhost:3306(2023/12/7更新)
有两种情况: 压根没安装下载了但没设为库或方法不对 大多数为第一种情况: 一. 下载jdbc 打开网址选择一个版本进行下载 https://nowjava.com/jar/version/mysql/mysql-connector-java.html 二.安装jdbc 在项目里建一个lib文件夹 在把之前下载的jar文…...

word文档中数字格式转换(排版助手)
示例:李老师收入了234243.33元,产量3000公斤; 张老师收入了2324324元,产量45555公斤; 孙老师收入了600000元,产量2342公斤 王老师收入了1234443243元,产量1243142公斤。 1、数字批量转换成千…...

阿里云docker加速
文章目录 一、 阿里云镜像仓库配置二、配置加速1. CentOS2. Mac3. Windows注意 一、 阿里云镜像仓库配置 1.注册阿里云账号,并登陆到阿里云后台,进入控制台面板 2.进入控制台以后,找到左上方的三横的功能列表按钮,在弹出来的功能…...

Panalog 日志审计系统 sprog_deletevent.php SQL 注入漏洞复现
0x01 产品简介 Panalog大数据日志审计系统定位于将大数据产品应用于高校、 公安、 政企、 医疗、 金融、 能源等行业之中,针对网络流量的信息进行日志留存,可对用户上网行为进行审计,逐渐形成大数据采集、 大数据分析、 大数据整合的工作模式…...

openGauss学习笔记-152 openGauss 数据库运维-备份与恢复-物理备份与恢复之PITR恢复
文章目录 openGauss学习笔记-152 openGauss 数据库运维-备份与恢复-物理备份与恢复之PITR恢复152.1 背景信息152.2 前提条件152.3 PITR恢复流程152.4 recovery.conf文件配置**152.4.1 归档恢复配置****152.4.2 恢复目标设置** openGauss学习笔记-152 openGauss 数据库运维-备份…...
PhpStorm基本配置及常用快捷键
重要Preference配置 激活服务器 http://jetbrains.tencent.click/http://owo.helphttp://idea.imsxm.com/http://www.0-php.com:10172017.3以上版本 JetBrains IDE 2017.3以上版本,激活检测机制变成了动态封禁域名,导致大部分域名激活被屏蔽了࿰…...

Autosar通信实战系列05-CanNM模块进阶常见问题思考
本文框架 前言1. UDS 0x28服务控制Nm报文收发后对状态机有影响?2. 节点网络启动后第一帧是否必须是网络管理报文?3. 主动唤醒后发送的第一帧报文为NM报文如何配置?4. CanNmMsgCycleOffset的使用场景?5. 什么情况下CBV中RepeatMessageRequest Bit置位?6. 主动(本地)唤醒与…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
