当前位置： 首页 > news >正文

ubuntu-c++-可执行模块-动态链接库-链接库搜索-基础知识

news 2025/12/26 7:56:23

文章目录

    • 1.动态链接库简介
    • 2.动态库搜索路径
    • 3.运行时链接及搜索顺序
    • 4.查看可运行模块的链接库
    • 5.总结

1.动态链接库简介

动态库又叫动态链接库，是程序运行的时候加载的库，当动态链接库正确安装后，所有的程序都可以使用动态库来运行程序。动态库是目标文件的集合，目标文件在动态库中的组织方式是按特殊的方式组织形成的。在动态库中函数和变量的地址是相对地址而不是绝对地址，其真实地址在调用动态库的程序加载时形成的。
动态库的名字有别名(soname), 真名（realname）和链接名（linkername）。别名是由一个lib前缀，然后是库的名字，最后以“.so”结尾来构成。真名是动态链接库的真实名字，一般总是在别名的基础上添加一个版本号信息。除此之外还有一个链接名，他是在程序链接的时候使用的名字。
动态库安装的时候，总是复制库文件到某一个目录，然后使用一个软链接生成一个别名，在库文件更新的时候，仅仅更新软链接即可。

2.动态库搜索路径

（仅对ELF格式）如果可执行文件包含DT_RPATH标签，并且不包含DT_RUNPATH标签，将从DT_RPATH列出的路径搜索。（DT_RPATH已经被废弃，请用DT_RUNPATH）
如果LD_LIBRARY_PATH在程序运行时被定义，那么将从它包含的路径开始。安全起见，对于set-user-ID或者set-group-ID的程序，这个变量将被忽略。
（仅对ELF格式）如果可执行文件包含DT_RUNPATH标签，将从这个标签列出的路径开始搜索。
从 /etc/ld.so.cache（运行ldconfig产生）中查找文件
从/lib以及/urs/lib，按顺序搜索。如果链接时指定-z nodefaultlib,这个步骤将被忽略。

3.运行时链接及搜索顺序

这个过程是由ld-linux.so程序来执行，这个才是真正的链接。它所做的工作就是将动态库的代码映射到进程的虚拟地址空间中，供进程来调用。程序在连接时使用了共享库，就必须在运行的时候能够找到共享库的位置。linux的可执行程序在执行的时候默认是先搜索/lib和/usr/lib这两个目录，然后按照/etc/ld.so.conf里面的配置搜索绝对路径。同时，Linux也提供了环境变量LD_LIBRARY_PATH供用户选择使用，用户可以通过设定它来查找除默认路径之外的其他路径，LD_LIBRARY_PATH路径优先于系统默认路径之前查找。

LD_LIBRARY_PATH的设定作用是全局的，过多的使用可能会影响到其他应用程序的运行，所以多用在调试。通常情况下推荐还是使用gcc的-R或-rpath选项来在编译时就指定库的查找路径，并且该库的路径信息保存在可执行文件中，运行时它会直接到该路径查找库，避免了使用LD_LIBRARY_PATH环境变量查找！！（看到Qt的使用qmake生成的makefile中，有gcc -rpath xxx，指出程序运行时的一个搜索路径, 或许与qt的QMAKE_RPATHDIR有关）

ld-linux.so.x在可执行的目标文件中被指定，可用readelf -l命令查看 。
(很多现代应用都是通过动态编译链接的，当一个 需要动态链接 的应用被操作系统加载时，系统必须要 定位 然后 加载它所 需要的所有动态库文件。 在Linux环境下，这项工作是由ld-linux.so.x来负责完成的)
和Windows下的PE文件类似，ELF文件是linux系统下可执行文件、动态库文件、静态库文件的标准格式。

例如，运行readelf -l 文件名，在输出的Headers部分的INTERP部分，会指出该可执行文件需要的ld-linux.so。
在这里插入图片描述

运行时，ld-linux.so 查找共享库的路径:
（1）编译时使用gcc的-R或-rpath选项指定路径。
（2）LD_LIBRARY_PATH环境变量中所设定的路径。
（3）ld-linux.so 缺省在/usr/lib和/lib中搜索；当glibc安装到/usr/local下时，它查找/usr/local/lib
（4）/etc/ld.so.conf（或/usr/local/etc/ld.so.conf）中所指定的路径。 （查看/etc/ld.so.conf文件：或许只有一行：“include /etc/ld.so.conf.d/*.conf ”，意味着包括了/etc/ld.so.conf.d/目录下的所有.conf文件，每个文件中都写着具体的路径。如果你想加一个运行时的搜索路径，可在/etc/ld.so.conf.d目录下新建一个.conf文件，里面写上路径，注意添加完了之后要在root权限下运行ldconfig指令，使其生效，该指令更新记录了系统中有哪些so文件的缓存文件（/etc /ld.so.cache）。）

4.查看可运行模块的链接库

可使用ldd指令查看一个可执行文件依赖于哪些库：ldd xxx

ldd  bash

在这里插入图片描述
linux-vdso.so.1是Linux为了解决和glibc兼容而想出的绝招。
原来这个 linux-vdso.so.1 文件，并不是一个真实存在的文件，而是 Linux 中的一个虚拟文件，专门用于将内核中一些常用的函数从内核空间映射到用户空间。也就是说，这个文件不用复制。
VDSO就是Virtual Dynamic Shared Object，就是内核提供的虚拟的.so，这个.so文件不在磁盘上，而是在内核里。内核把包含某.so的内存页在程序启动的时候映射入其内存空间，对应的程序就可以当普通的.so来使用其提供的函数接口。

5.总结

在linux下的动态链接库并不从程序所在当前目录查找连接库，而是从编译时指定目录查找，或者默认目录查找。

相关文章：

ubuntu-c++-可执行模块-动态链接库-链接库搜索-基础知识

文章目录 1.动态链接库简介2.动态库搜索路径3.运行时链接及搜索顺序4.查看可运行模块的链接库5.总结 1.动态链接库简介 动态库又叫动态链接库，是程序运行的时候加载的库，当动态链接库正确安装后，所有的程序都可以使用动态库来运行程序。动态…...

编程日记 2023/12/12 9:52:42

HTML中使用JavaScript实现一个简单的鼠标悬停特效。

代码中&#xff0c;我们首先在CSS中定义了一个红色的方块&#xff0c;然后使用:hover伪类定义了鼠标悬停时的样式。接着&#xff0c;在JavaScript中定义了一个函数showMessage()&#xff0c;用于在控制台输出一条消息。最后&#xff0c;在HTML中使用<div>标签定义了一个i…...

编程日记 2023/12/12 9:51:42

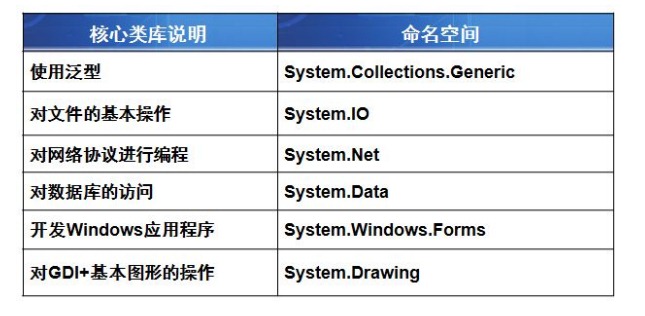
深入.NET平台和C#编程总结大全

第一章 简单认识.NET框架 &#xff08;1&#xff09;首先我们得知道 .NET框架具有两个主要组件&#xff1a;公共语言进行时CLR&#xff08;Common Language Runtime&#xff09;和框架类库FCL&#xff08;Framework Class Library&#xff09; 配图&#xff1a; &#xff08;…...

编程日记 2023/12/12 9:49:40

jOOQ的使用场景

jOOQ的使用场景 jOOQ最初是作为一个库完全是JDBC和所有的数据库交互的抽象层而被创建。 在已有的软件产品中经常遇到的各种最佳实践被应用到这个库中。包含如下&#xff1a; 类型安全数据库对象引用&#xff0c;通过自动生成的模式&#xff0c; 表&#xff0c; 列&#xff0c…...

编程日记 2023/12/12 9:48:39

Pytorch-Transformer轴承故障一维信号分类(三)

目录 前言 1 数据集制作与加载 1.1 导入数据 第一步&#xff0c;导入十分类数据 第二步&#xff0c;读取MAT文件驱动端数据 第三步&#xff0c;制作数据集 第四步&#xff0c;制作训练集和标签 1.2 数据加载&#xff0c;训练数据、测试数据分组&#xff0c;数据分batch…...

编程日记 2023/12/12 9:47:38

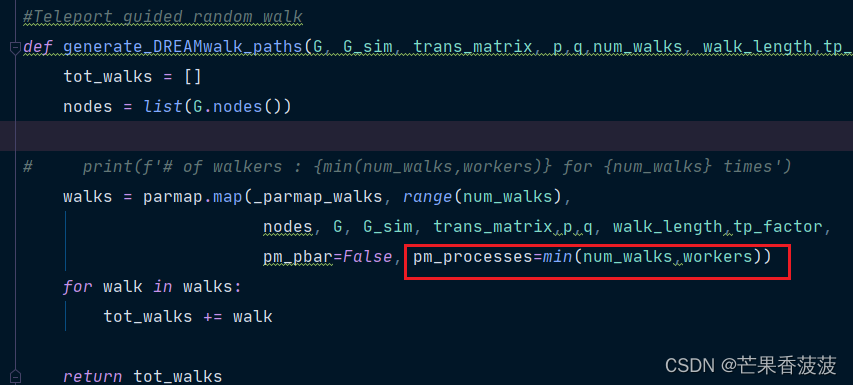
pycharm多线程报错的问题（未解决）

暂未解决&#xff01; 看了一下可能是这里的问题&#xff1a; 根据建议&#xff0c;在walks之前加了 freeze_support() 但是没有效果。 关键是&#xff0c;在jupyter上运行是没有问题的&#xff01; 未解决。...

编程日记 2023/12/12 9:44:36

【常用字符大全】含emoji表情

常用符号大全 ❤❥웃유♋☮✌☏☢☠✔☑♚▲♪✈✞↑↓◆◇⊙■□△▽─│♥❣♂♀☿Ⓐ✍✉☣☤✘☒♛▼♫⌘☪≈←→◈◎☉★☆⊿※¡━┃♡ღツ☼☁❅♒✎©™Σ✪✯☭➳卐√↖↗●◐Θ◤◥︻〖〗┄┆℃℉✿ϟ☃☂✄¢€£∞✫★✡↙↘○◑⊕◣◢︼【】┅┇…...

编程日记 2023/12/12 9:42:34

android 蓝牙开关设置

frameworks/base/packages/SettingsProvider/res/values/defaults.xml <bool name"def_bluetooth_on">false</bool>将 def_bluetooth_on 的值设为false&#xff08;系统默认开启值&#xff09; adb动态设置 关闭&#xff1a;adb shell settings put gl…...

编程日记 2023/12/12 9:41:33

C++ extern “C“ 用法

extern “C” 由于c中需要支持函数重载&#xff0c;所以c和c中对同一个函数经过编译后生成的函数名是不相同的 extern “C” 的主要作用就是为了实现c代码能够调用其他 c 语言代码。 1(不常用) //告诉编译器 show() 函数按c语言的方式进行编译和链接 extern "C" voi…...

编程日记 2023/12/12 9:39:31

HTML面试题---专题四

文章目录 一、前言二、如何在 HTML 中嵌入音频文件&#xff1f;三、解释 <script> 标签中 defer 属性的用途。四、如何在 HTML 中创建粘性/固定导航栏&#xff1f;五、HTML 中的 span 元素的用途是什么&#xff1f;六、如何使 HTML 元素可拖动&#xff1f;七、解释 <i…...

编程日记 2023/12/12 9:38:30

stm32项目（11）——基于stm32的俄罗斯方块游戏机

1.功能设计 使用stm32f103zet6平台&#xff0c;以及一块LCD屏幕&#xff0c;实现了一个俄罗斯方块游戏机。可以用按键调整方块的位置、还可以控制方块下降的速度&#xff01; 2.视频演示 俄罗斯方块 3.俄罗斯方块发展史 俄罗斯方块是一种经典的拼图游戏&#xff0c;由苏联俄罗…...

编程日记 2023/12/12 9:37:28

【计算机网络基础2】IP地址和子网掩码

1、IP地址 网络地址 IP地址由网络号&#xff08;包括子网号&#xff09;和主机号组成&#xff0c;网络地址的主机号为全0&#xff0c;网络地址代表着整个网络。 广播地址 广播地址通常称为直接广播地址&#xff0c;是为了区分受限广播地址。 广播地址与网络地址的主机号正…...

编程日记 2023/12/12 9:33:25

ES6-import后是否有{}的区别

在ES6中&#xff0c;import语句用于导入其他模块中的变量、函数、类等。在使用import语句时&#xff0c;可以选择是否使用花括号{}来包裹导入的内容&#xff0c;这会影响导入的内容的使用方式。 1.使用花括号{}&#xff1a; 当使用花括号{}时&#xff0c;表示只导入指定的变量…...

编程日记 2023/12/12 9:29:22

rv1126-rv1109-以太网功能-eth-(原理篇)

这里只是浅浅分析一下 1.主控里面会内置mac 2.mac有组接口接到phy(网络芯片:8201) 3.phy(网络芯片:8201)接到网口 //这里就到达硬件的接口了,大致就是这个原理; 4.然后涉及到软件部分 就是mdio总线;这个总线是注册phy用的; 如果注册失败会导致网口无法使用 [ 1.002751] m…...

编程日记 2023/12/12 9:27:20

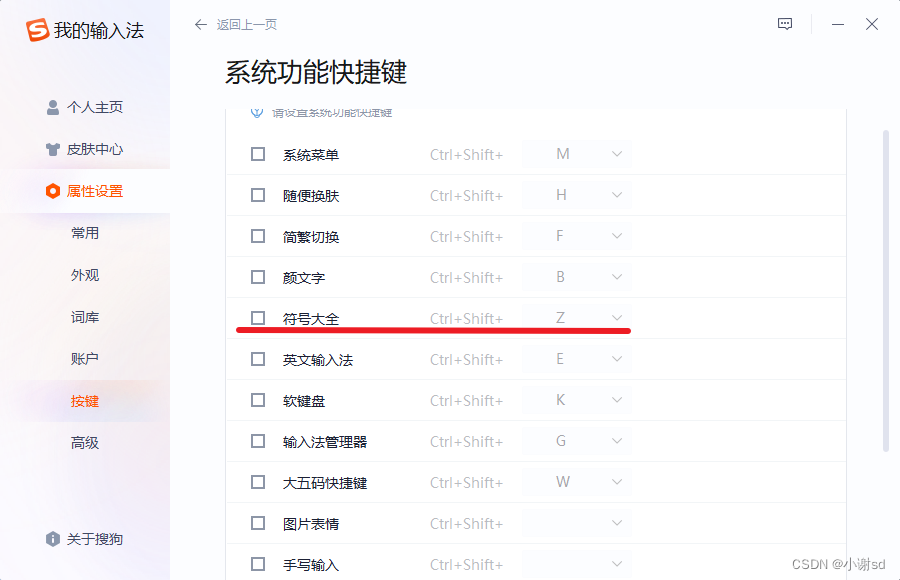
【IDEA】反向撤销操作快捷键 ctrl+shift+z 和搜狗热键冲突的解决办法

当我们执行某些操作时与搜狗热键冲突&#xff0c;直接取消搜狗的快捷键即可&#xff01;&#xff01;&#xff01;以下以 ctrlshiftz 为例。 在输入悬浮框右键找到更多设置 按键里面找到系统功能快捷键设置 取消掉冲突的热键即可...

编程日记 2023/12/12 9:21:15

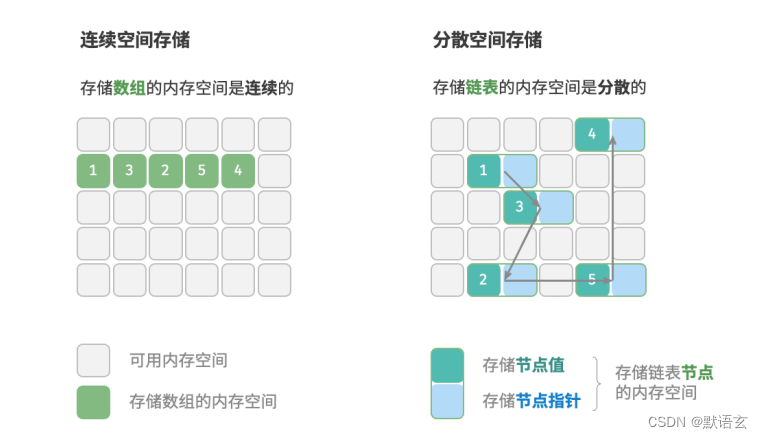
数据结构之----逻辑结构、物理结构

数据结构之----逻辑结构、物理结构 目前我们常见的数据结构分别有&#xff1a; 数组、链表、栈、队列、哈希表、树、堆、图 而它们可以从 逻辑结构和物理结构两个维度进行分类。 什么是逻辑结构&#xff1f; 逻辑结构是指数据元素之间的逻辑关系&#xff0c;而逻辑结构又分为…...

编程日记 2023/12/12 9:20:15

pip 通过git安装库

举例&#xff1a;安装peft库 git clone https://github.com/huggingface/peft.git cd peft python -m pip install . 解释&#xff1a; 使用git clone克隆PEFT库的代码。进入克隆的目录。使用python -m pip install .来安装PEFT库。 补充&#xff1a;使用pip安装到指定编译器…...

编程日记 2023/12/12 9:19:13

C语言——从终端输入 3 个数 a、b、c，按从大到小的顺序输出。

方式一 #include <stdio.h> int main() {int a, b, c, temp;printf("请输入三个数&#xff1a;\n");scanf("%d %d %d", &a, &b, &c);if (a < b) {temp a;a b;b temp;}if (a < c) {temp a;a c;c temp;}if (b < c) {temp…...

编程日记 2023/12/12 9:17:11

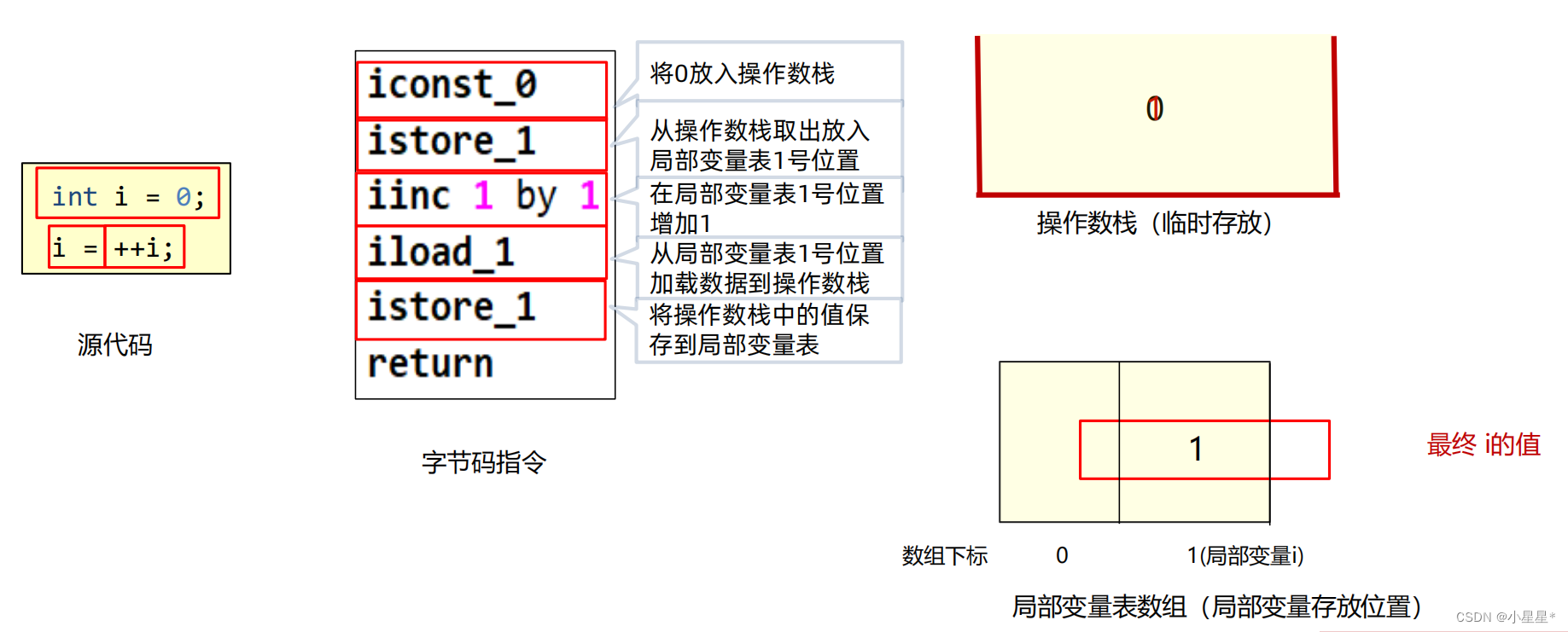
【JVM从入门到实战】（二）字节码文件的组成

一、Java虚拟机的组成 二、字节码文件的组成 字节码文件的组成 – 应用场景 字节码文件的组成部分-Magic魔数 什么是魔数&#xff1f; Java字节码文件中的魔数 文件是无法通过文件扩展名来确定文件类型的&#xff0c;文件扩展名可以随意修改&#xff0c;不影响文件的内容。…...

编程日记 2023/12/12 9:16:10

OPC UA常见故障信息代码

错误信息解释0x00000000操作成功。0x40000000值不确定&#xff0c;但原因不明。0x80000000值为坏&#xff0c;但原因不明。Bad_UnexpectedError 0x80010000发生非预期错误。Bad_InternalError 0x80020000编程或配置错误时发生内部错误。Bad_OutOfMemory 0x80030000完成操作所需…...

编程日记 2023/12/12 9:12:05

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式

一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明&#xff1a;假设每台服务器已…...

编程新知 2025/12/25 19:27:00

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造&#xff0c;完美适配AGV和无人叉车。同时&#xff0c;集成以太网与语音合成技术&#xff0c;为各类高级系统&#xff08;如MES、调度系统、库位管理、立库等&#xff09;提供高效便捷的语音交互体验。 L…...

编程新知 2025/12/26 6:10:22

调用支付宝接口响应40004 SYSTEM_ERROR问题排查

在对接支付宝API的时候&#xff0c;遇到了一些问题&#xff0c;记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

编程新知 2025/12/22 11:37:06

SpringCloudGateway 自定义局部过滤器

场景&#xff1a; 将所有请求转化为同一路径请求&#xff08;方便穿网配置&#xff09;在请求头内标识原来路径&#xff0c;然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

编程新知 2025/12/15 1:25:04

QT： `long long` 类型转换为 `QString` 2025.6.5

在 Qt 中&#xff0c;将 long long 类型转换为 QString 可以通过以下两种常用方法实现&#xff1a; 方法 1&#xff1a;使用 QString::number() 直接调用 QString 的静态方法 number()&#xff0c;将数值转换为字符串&#xff1a; long long value 1234567890123456789LL; …...

编程新知 2025/12/14 4:20:34

聊一聊接口测试的意义有哪些？

目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开&#xff0c;首…...

编程新知 2025/10/14 6:46:13

代理篇12|深入理解 Vite中的Proxy接口代理配置

在前端开发中，常常会遇到 跨域请求接口 的情况。为了解决这个问题，Vite 和 Webpack 都提供了 proxy 代理功能，用于将本地开发请求转发到后端服务器。 什么是代理（proxy）？ 代理是在开发过程中，前端项目通过开发服务器，将指定的请求“转发”到真实的后端服务器，从而绕…...

编程新知 2025/10/27 20:33:34

Mobile ALOHA全身模仿学习

一、题目 Mobile ALOHA&#xff1a;通过低成本全身远程操作学习双手移动操作 传统模仿学习&#xff08;Imitation Learning&#xff09;缺点&#xff1a;聚焦与桌面操作&#xff0c;缺乏通用任务所需的移动性和灵活性 本论文优点&#xff1a;&#xff08;1&#xff09;在ALOHA…...

编程新知 2025/12/9 12:23:34

IP如何挑？2025年海外专线IP如何购买？

你花了时间和预算买了IP&#xff0c;结果IP质量不佳&#xff0c;项目效率低下不说&#xff0c;还可能带来莫名的网络问题&#xff0c;是不是太闹心了&#xff1f;尤其是在面对海外专线IP时&#xff0c;到底怎么才能买到适合自己的呢&#xff1f;所以&#xff0c;挑IP绝对是个技…...

编程新知 2025/10/19 9:49:56

20个超级好用的 CSS 动画库

分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码&#xff0c;而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库&#xff0c;可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画&#xff0c;可以包含在你的网页或应用项目中。 3.An…...

编程新知 2025/12/24 6:32:57