推荐算法:HNSW【推荐出与用户搜索的类似的/用户感兴趣的商品】
HNSW算法概述
HNSW(Hierarchical Navigable Small Word)算法算是目前推荐领域里面常用的ANN(Approximate Nearest Neighbor)算法了。其目的就是在极大量的候选集当中如何快速地找到一个query最近邻的k个元素。
要找到一个query的k个最近邻元素,一个朴素的思想就是我去计算这个query和所有的总量N 个候选元素的距离,然后选择其中的前k 个最小元素,这个经典算法的算法复杂度是O(Nlog(k)),显然这个算法复杂度实在是太高了,无法适用于实际的使用场景。
而要解决这个问题,可以有多种实现方法,这里所要说的HNSW算法就是目前比较常用的一种搜索算法,它算是其前作NSW算法的一个升级版本,但是两者的本质都是基于一个朴素的思路,就是通过图连接的方式给所有的N 个候选元素事先地定义好一个图连接关系,从而可以将前述的算法复杂度当中的N 的部分给减小掉,从而优化整体的检索效率。
其整体的一个图结果可以用下图进行表达:

解决的问题:做高效率相似性查找。推荐系统中,如何找到与用户query最相近的几个item,然后推荐出去【也就是推荐出与用户搜索的类似的/用户感兴趣的商品】。
解决方法有:Annoy,KD-Tree, LSH, PQ,NSW, HNSW等。
近似最近邻搜索算法(Approximate Nearest Neighbor Search,ANNS)发展:近邻图(Proximity Graph)–> NSW --> Skip List --> HNSW
近似最近邻搜索算法(Approximate Nearest Neighbor Search,ANNS)
1. 近邻图(Proximity Graph)
近邻图(Proximity Graph): 最朴素的图算法
思路: 构建一张图, 每一个顶点连接着最近的 N 个顶点。 Target (红点)是待查询的向量。在搜索时, 选择任意一个顶点出发。 首先遍历它的友节点, 找到距离与 Target 最近的某一节点, 将其设置为起始节点, 再从它的友节点出发进行遍历, 反复迭代, 不断逼近, 最后找到与 Target 距离最近的节点时搜索结束。

存在的问题:
- 图中的K点无法被查询到。
- 如果要查找距离Target (红点)最近的topK个点, 而如果点之间无连线, 将影响查找效率。
- D点有这么多友节点吗? 增加了构造复杂度。谁是谁的友节点如何确定?
- 如果初始点选择地不好(比如很远),将进行多步查找。
2. NSW算法原理
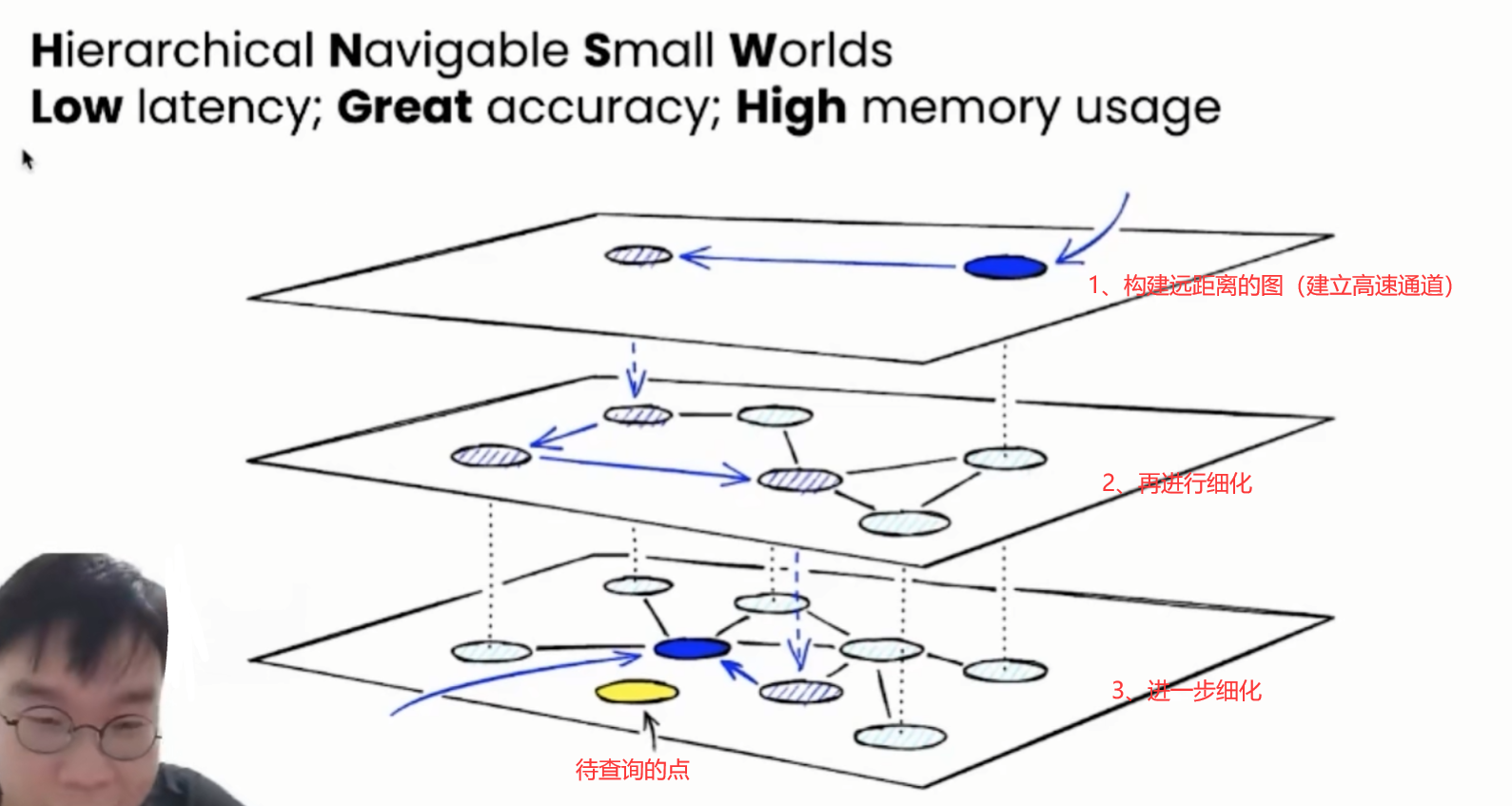
NSW,即没有分层的可导航小世界的结构(Navigable-Small-World-Graph )。
针对上面的问题,解决办法:
- 某些点无法被查询到 -> 规定构图时所有节点必须有友节点。
- 相似点不相邻的问题 -> 规定构图时所有距离相近到一定程度的节点必须互为友节点。
- 关于某些点有过多友节点 -> 规定限制每个节点的友节点数量。
- 初始点选择地很远 -> 增加高速公路机制。
2.1 NSW构图算法
图中插入新节点时,通过随机存在的一个节点出发查找到距离新节点最近的m个节点(规定最多m个友节点,m由用户设置),连接新节点到这最近的m个节点。节点的友节点在新的节点插入的过程中会不断地被更新。
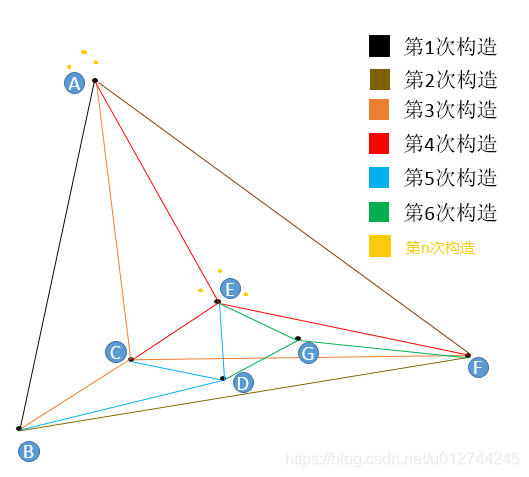
m=3(每个点在插入时找3个紧邻友点)。
第1次构造:图为空,随机插入A,初始点为A。图中只有A,故无法挑选友节点。插入B,B点只有A点可选,所以连接BA。
第2次构造:插入F,F只有A和B可以选,所以连接FA,FB。
第3次构造:插入C,C点只有A,B,F可选,连接CA,CB,CF。
第4次构造:插入E,从A,B,C,F任意一点出发,计算出发点与E的距离和出发点的所有“友节点”和E的距离,选出最近的一点作为新的出发点,如果选出的点就是出发点本身,那么看我们的m等于几,如果不够数,就继续找第二近的点或者第三近的点,本着不找重复点的原则,直到找到3个近点为止。找到了E的三个近点,连接EA,EC,EF。
第5次构造:插入D,与E点的插入一模一样,都是在“现成”的图中查找到3个最近的节点作为“友节点”,并做连接。
第6次构造:插入G,与E点的插入一模一样,都是在“现成”的图中查找到3个最近的节点作为“友节点”,并做连接。
在图构建的早期,很有可能构建出“高速公路”。
第n次构造:在这个图的基础上再插入6个点,这6个点有3个和E很近,有3个和A很近,那么距离E最近的3个点中没有A,距离A最近的3个点中也没有E,但因为A和E是构图早期添加的点,A和E有了连线,我们管这种连线叫“高速公路”,在查找时可以提高查找效率(当进入点为E,待查找距离A很近时,我们可以通过AE连线从E直接到达A,而不是一小步一小步分多次跳转到A)。
结论:一个点,越早插入就越容易形成与之相关的“高速公路”连接,越晚插入就越难形成与之相关的“高速公路”连接。
这个算法设计的妙处就在于扔掉德劳内三角构图法,改用“无脑添加”(NSW朴素插入算法),降低了构图算法时间复杂度的同时还带来了数量有限的“高速公路”,加速了查找。
2.2 NSW查找算法
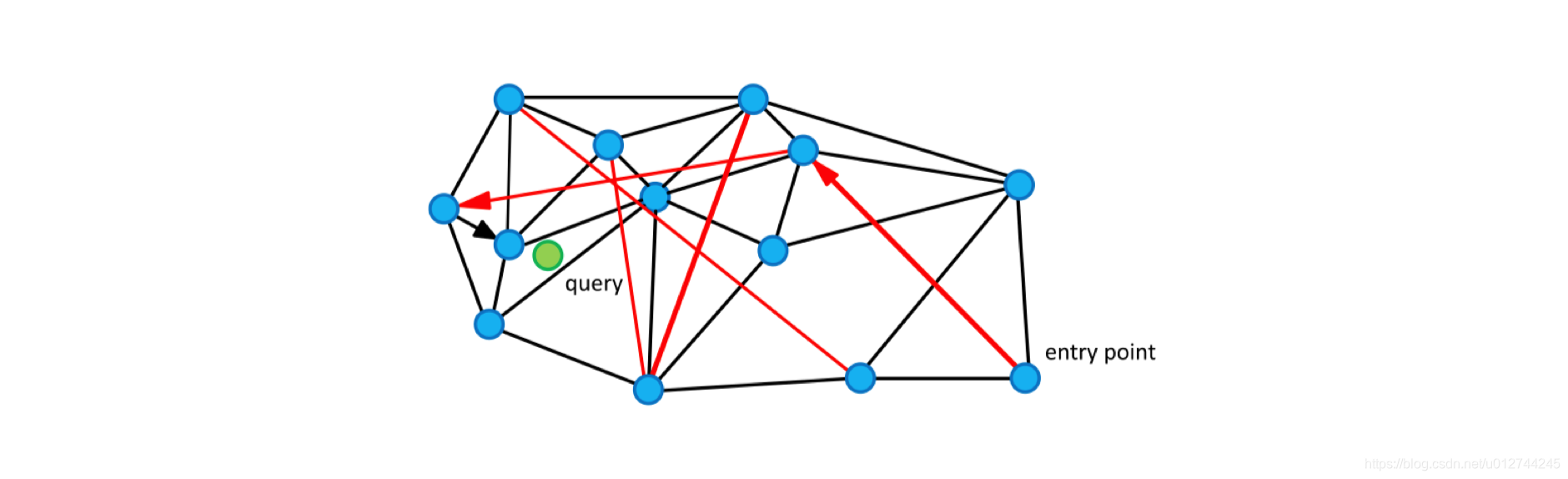
图中的边有两个不同的目的:
- Short-range edges,用作贪婪搜索算法所需的近似 Delaunay 图。
- Long-range edges,用于贪婪搜索的对数缩放。负责构造图形的可导航小世界(NSW)属性。
优化查找:
- 建立一个废弃列表visitedSet,在一次查找任务中遍历过的点不再遍历。
- 建立一个动态列表result,把距离查找点最近的n个点存储在表中,并行地对这n个点进行同时计算“友节点”和待查找点的距离,在这些“友节点”中选择n个点与动态列表中的n个点进行并集操作,在并集中选出n个最近的友点,更新动态列表。
推荐算法:HNSW算法简介-CSDN博客
检索模型-粗排HNSW_hnsw模型-CSDN博客
相关文章:

推荐算法:HNSW【推荐出与用户搜索的类似的/用户感兴趣的商品】
HNSW算法概述 HNSW(Hierarchical Navigable Small Word)算法算是目前推荐领域里面常用的ANN(Approximate Nearest Neighbor)算法了。其目的就是在极大量的候选集当中如何快速地找到一个query最近邻的k个元素。 要找到一个query的…...
C++ //例3.14 找出100~200间的全部素数。
C程序设计 (第三版) 谭浩强 例3.14 例3.14 找出100~200间的全部素数。 IDE工具:VS2010 Note: 使用不同的IDE工具可能有部分差异。 代码块 方法:使用函数的模块化设计 #include <iostream> #include <iomanip> #i…...
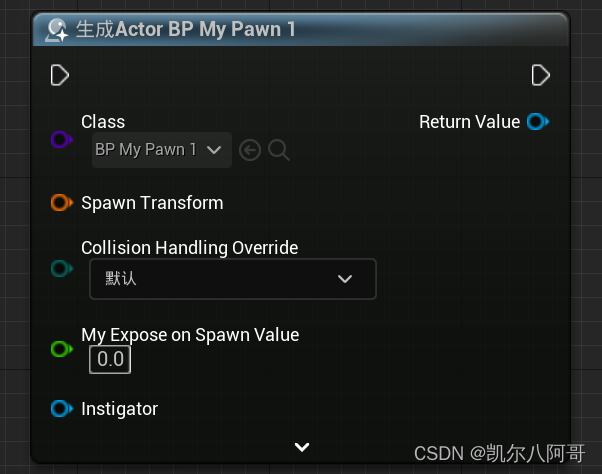
虚幻学习笔记11—C++结构体、枚举与蓝图的通信
一、前言 结构体的定义和枚举类似,枚举的定义有两种方式。区别是结构体必须以“F”开头命名,而枚举不用。 额外再讲了一下蓝图生成时暴露变量的方法。 二、实现 2.1、结构体 1、定义结构体 代码如下,注意这个定义的代码一定要在“UCLASS()”…...

【android开发-19】android中内容提供者contentProvider用法讲解
1,内容URI 在Android系统中,Content URI是一种用于唯一标识和访问应用程序中的数据的方法。它由Android系统提供,通过Content Provider来实现数据的共享和访问。 Content URI使用特定的格式来标识数据,通常以"content://&qu…...
)
浅谈排序——快速排序(最常用的排序)
快速排序(Quick Sort)是一种常见的排序算法,由英国计算机科学家东尼霍尔(Tony Hoare)在1960年发明。这是一种分治算法,基本思想是通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所…...

Springboot项目实现简单的文件服务器,实现文件上传+图片及文件回显
文章目录 写在前面一、配置1、application.properties2、webMvc配置3、查看效果 二、文件上传 写在前面 平常工作中的项目,上传的文件一般都会传到对象存储云服务中。当接手一个小项目,如何自己动手搭建一个文件服务器,实现图片、文件的回显…...

5V低压步进电机驱动芯片GC6150,应用于摄像机,机器人 医疗器械等产品中。具有低噪声、低振动的特点
GC6150是双通道5V低压步进电机驱动器,具有低噪声、低振动的特点,特别适用于相机变焦对焦系统、万向架、摇头机等精度、低噪声STM控制系统,该芯片为每个通道集成了一个256微步的驱动器。通过SPI & T2C接口,客户可以方使地调整驱…...
3D Web轻量引擎HOOPS Communicator如何实现对大模型的渲染支持?
除了读取轻松外,HOOPS Communicator对超大模型的支持效果也非常好,它可以支持30GB的包含70万个零件和3.5亿个三角面的Catia装配模型! 那么它是如何来实现对大模型的支持呢? 我们将从以下几个方面与大家分享:最低帧率…...
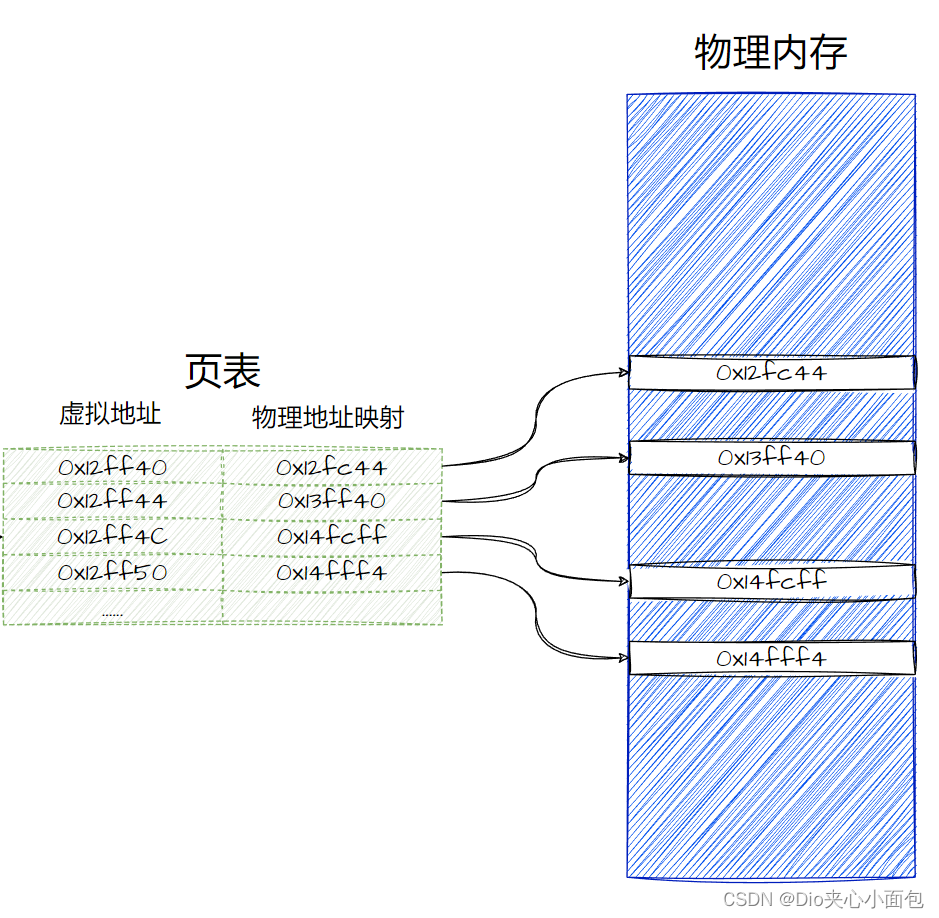
『 Linux 』进程地址空间概念
文章目录 🫙 前言🫙 进程地址空间是什么🫙 写时拷贝🫙 可执行程序中的虚拟地址🫙 物理地址分布方式 🫙 前言 在c/C中存在一种内存的概念; 一般来说一个内存的空间分布包括栈区,堆区,代码段等等; 且内存是…...

PySpark大数据处理详细教程
欢迎各位数据爱好者!今天,我很高兴与您分享我的最新博客,专注于探索 PySpark DataFrame 的强大功能。无论您是刚入门的数据分析师,还是寻求深入了解大数据技术的专业人士,这里都有丰富的知识和实用的技巧等着您。让我们…...
ts非基础类型(对象))
三(五)ts非基础类型(对象)
在ts里面定义对象的方式也有很多。 普通定义 let obj1:{} {} // obj1.name fufu 报错,只能定义为空对象且不能修改 // 但是可以在赋初始值的时候直接添加属性,这是ts在类型推断时,它会宽容地匹配对象的结构。 let obj2:{} {name: fufu}…...
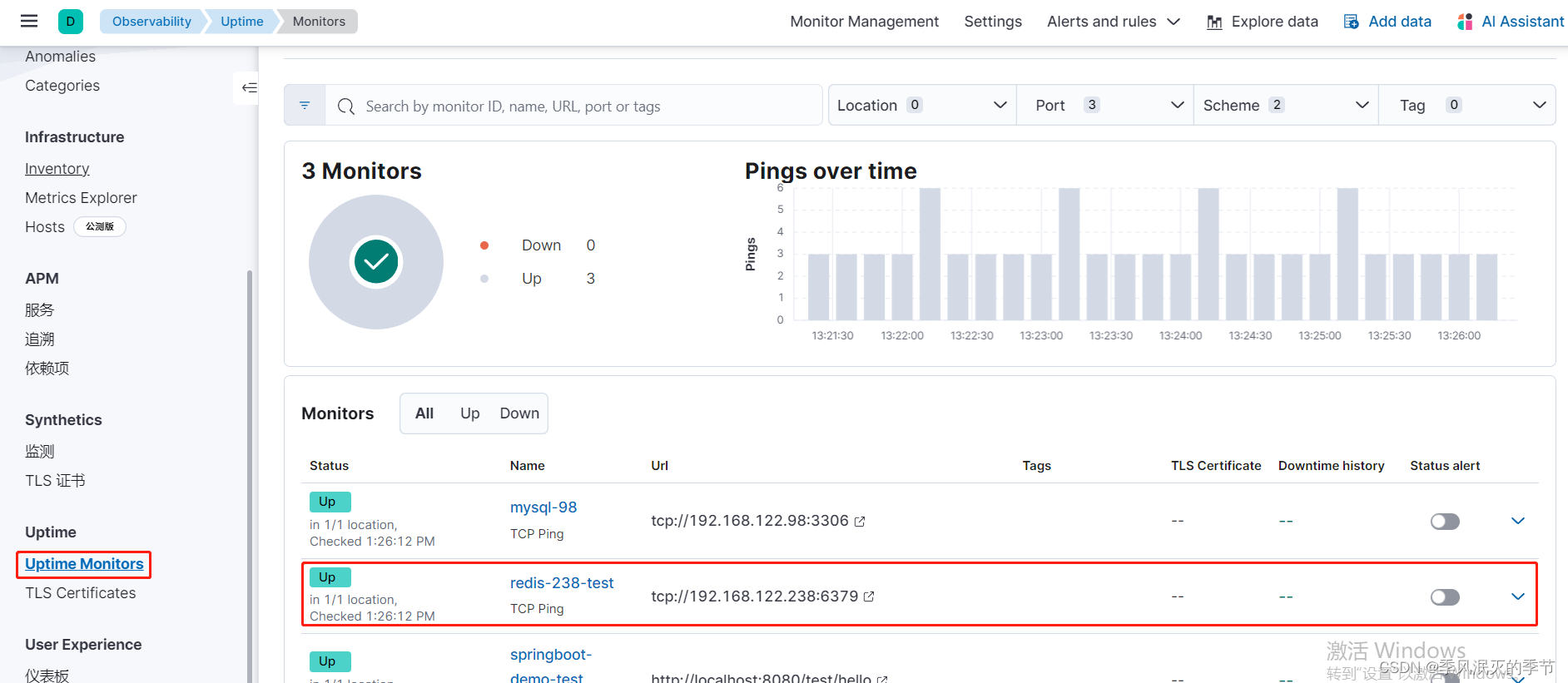
HeartBeat监控Redis状态
目录 一、概述 二、 安装部署 三、配置 四、启动服务 五、查看数据 一、概述 使用heartbeat可以实现在kibana界面对redis服务存活状态进行观察,如有必要,也可在服务宕机后立即向相关人员发送邮件通知 二、 安装部署 参照文章:HeartBeat监…...

FairGuard无缝兼容小米澎湃OS、ColorOS 14 、鸿蒙4!
随着移动互联网时代的发展,各大手机厂商为打造生态系统、构建自身的技术壁垒,纷纷投身自研操作系统。 而对于一款游戏安全产品,在不同操作系统下,是否能够无缝兼容并且提供稳定的、高强度的加密保护,成了行业的一大痛…...
【Copilot】Edge浏览器的copilot消失了怎么办
这种原因,可能是因为你的ip地址的不在这个服务的允许范围内。你需要重新使用之前出现copilot的ip地址,然后退出edge的账号,重新登录一遍,最后重启edge,就能够使得copilot侧边栏重新出现了。...

C++入门【6-C++ 修饰符类型】
C 修饰符类型 C 允许在 char、int 和 double 数据类型前放置修饰符。 修饰符是用于改变变量类型的行为的关键字,它更能满足各种情境的需求。 下面列出了数据类型修饰符: signed:表示变量可以存储负数。对于整型变量来说,signe…...

STP笔记总结
STP --- 生成树协议 STP(Spanning Tree Protocol,生成树协议)是根据 IEEE802.1D标准建立的,用于在局域网中消除数据链路层环路的协议。运行STP协议的设备通过彼此交互信息发现网络中的环路,并有选择地对某些端口进行阻…...
Qt开发 之 记一次安装 Qt5.12.12 安卓环境的失败案例
文章目录 1、安装Qt2、安卓开发的组合套件2.1、CSDN地址2.2、官网地址2.3、发现老方法不适用了 3、尝试用新方法解决3.1、先安装JDK,搞定JDK环境变量3.1.1、安装jdk3.1.2、确定jdk安装路径3.1.3、打开系统环境变量配置3.1.4、配置系统环境变量3.1.5、验证JDK环境变量…...
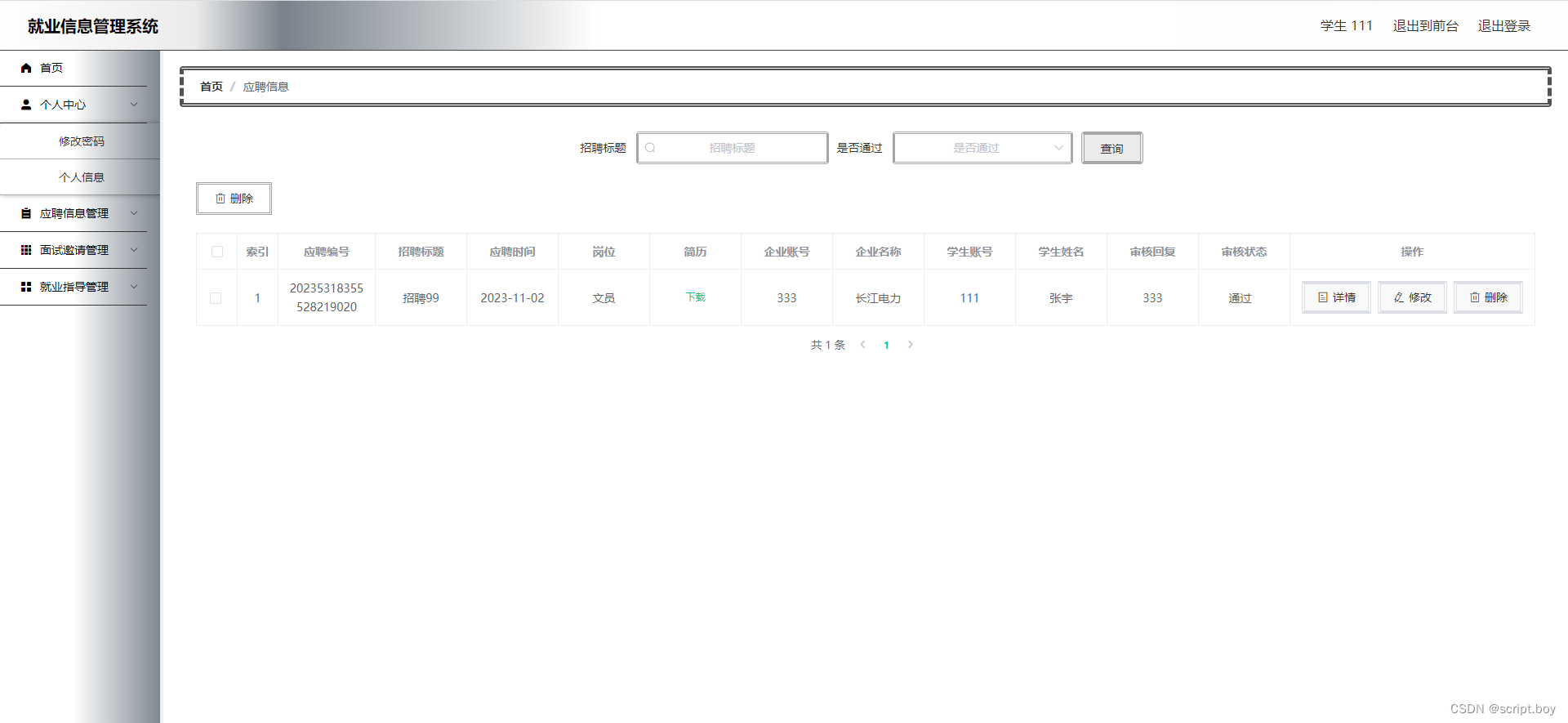
基于SpringBoot的就业信息管理系统设计与实现(源码+数据库+文档)
摘 要 在新冠肺炎疫情的影响下,大学生的就业问题已经变成了一个引起人们普遍重视的社会焦点问题。在这次疫情的冲击之下,大学生的就业市场的供求双方都受到了不同程度的影响,大学生的就业情况并不十分乐观。目前,各种招聘平台上…...
Java IO流)
Java面试整理(四)Java IO流
我记得自己刚开始学Java的时候,都听过师兄的分享,说IO流是很重要,而且很难。 自己正式接触之后,其实IO流这块知识并不是特别难,而且随着IT的发展,IO流这块反而用得不是很多。特别是在应用开发这个层面,用得更少。 当然,可能会有朋友跳出来说“这怎么可能?你不懂Java吧…...
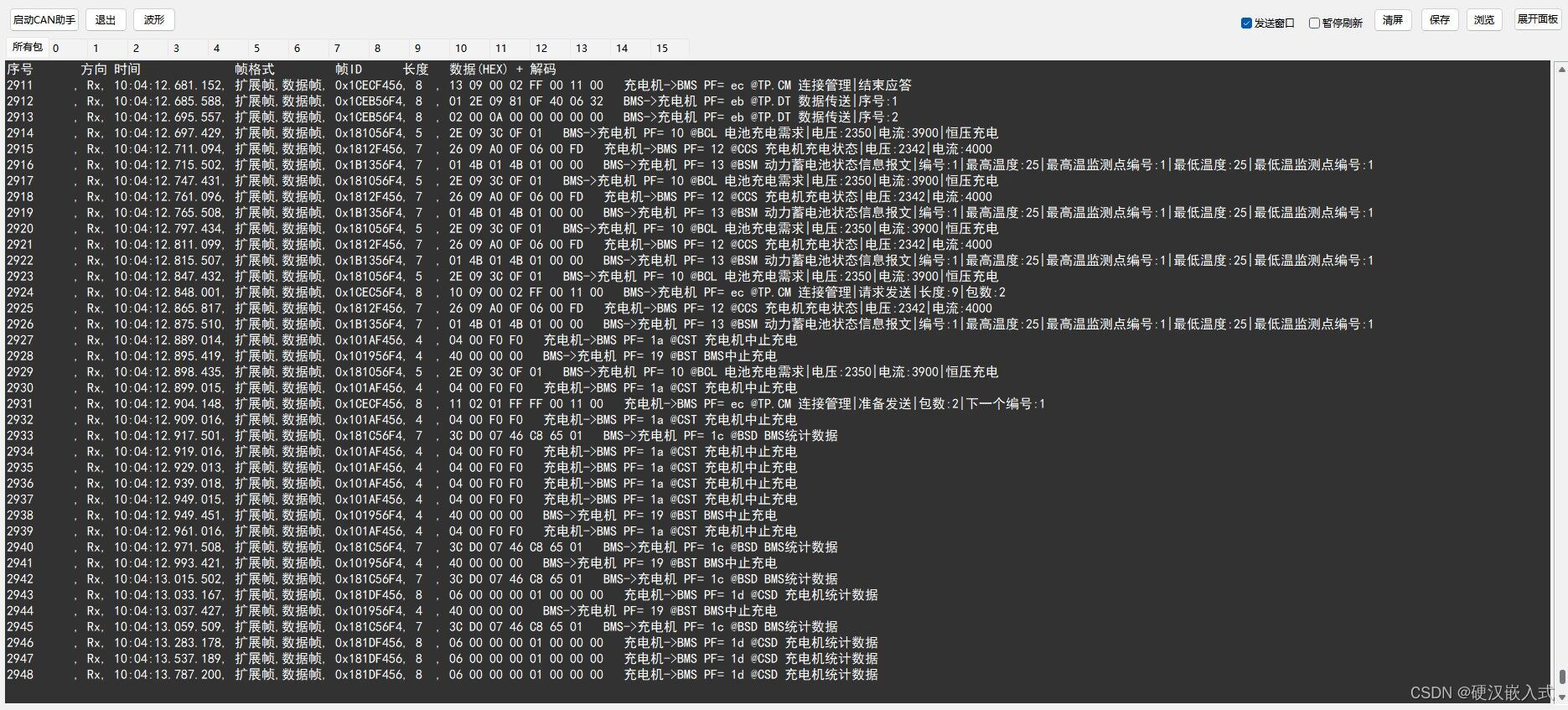
《安富莱嵌入式周报》第328期:自主微型机器人,火星探测器发射前失误故障分析,微软推出12周24期免费AI课程,炫酷3D LED点阵设计,MDK5.39发布
周报汇总地址:嵌入式周报 - uCOS & uCGUI & emWin & embOS & TouchGFX & ThreadX - 硬汉嵌入式论坛 - Powered by Discuz! 更新一期视频教程: 【实战技能】 单步运行源码分析,一期视频整明白FreeRTOS内核源码框架和运行…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...
