渐进推导中常用的一些结论
标题很帅
STAR-RIS Enhanced Joint Physical Layer Security and Covert Communications for Multi-antenna mmWave Systems文章末尾的一个推导。
lim M → ∞ ∥ Φ ( w k ⊗ Θ r ) Ω r w H g ∗ ∥ 2 2 M = lim M → ∞ Tr ( g T Ω r w ( w k ⊗ Θ r ) H Φ H Φ ( w k ⊗ Θ r ) Ω r w H g ∗ ) M → ( a ) Tr ( Ω r w H Ω r w ( w k ⊗ Θ r ) H Φ H Φ ( w k ⊗ Θ r ) ) M = ( b ) Tr ( ∑ l = 1 L ( w k H Ψ B R l w k ) ⊗ ( Ω r w H Ω r w Θ r H Ψ ^ B R l Θ r ) ) M = ( c ) ∑ l = 1 L ( w k H Ψ B R l w k ) Tr ( Ω r w H Ω r w Θ r H Ψ ^ B R l Θ r ) M = ∑ l = 1 L ( w k H Ψ B R l w k ) ( ϑ r T Ξ T ( ( Ψ ^ B R l ) T ⊗ ( Ω r w H Ω r w ) ) Ξ ϑ r ∗ ) M , \begin{array}{l} \lim _{M \rightarrow \infty} \frac{\left\|\boldsymbol{\Phi}\left(\mathbf{w}_{k} \otimes \boldsymbol{\Theta}_{\mathrm{r}}\right) \boldsymbol{\Omega}_{\mathrm{rw}}^{H} \mathbf{g}^{*}\right\|_{2}^{2}}{M} \\ =\lim _{M \rightarrow \infty} \frac{\operatorname{Tr}\left(\mathbf{g}^{T} \boldsymbol{\Omega}_{\mathrm{rw}}\left(\mathbf{w}_{k} \otimes \boldsymbol{\Theta}_{\mathrm{r}}\right)^{H} \mathbf{\Phi}^{H} \boldsymbol{\Phi}\left(\mathbf{w}_{k} \otimes \boldsymbol{\Theta}_{\mathrm{r}}\right) \boldsymbol{\Omega}_{\mathrm{rw}}^{H} \mathbf{g}^{*}\right)}{M} \\ \stackrel{(a)}{\rightarrow} \frac{\operatorname{Tr}\left(\boldsymbol{\Omega}_{\mathrm{rw}}^{H} \boldsymbol{\Omega}_{\mathrm{rw}}\left(\mathbf{w}_{k} \otimes \boldsymbol{\Theta}_{\mathrm{r}}\right)^{H} \boldsymbol{\Phi}^{H} \boldsymbol{\Phi}\left(\mathbf{w}_{k} \otimes \boldsymbol{\Theta}_{\mathrm{r}}\right)\right)}{M} \\ \stackrel{(b)}{=} \frac{\operatorname{Tr}\left(\sum_{l=1}^{L}\left(\mathbf{w}_{k}^{H} \mathbf{\Psi}_{\mathrm{BR}}^{l} \mathbf{w}_{k}\right) \otimes\left(\boldsymbol{\Omega}_{\mathrm{rw}}^{H} \boldsymbol{\Omega}_{\mathrm{rw}} \boldsymbol{\Theta}_{\mathrm{r}}^{H} \widehat{\mathbf{\Psi}}_{\mathrm{BR}}^{l} \boldsymbol{\Theta}_{\mathrm{r}}\right)\right)}{M} \\ \stackrel{(c)}{=} \frac{\sum_{l=1}^{L}\left(\mathbf{w}_{k}^{H} \mathbf{\Psi}_{\mathrm{BR}}^{l} \mathbf{w}_{k}\right) \operatorname{Tr}\left(\boldsymbol{\Omega}_{\mathrm{rw}}^{H} \boldsymbol{\Omega}_{\mathrm{rw}} \boldsymbol{\Theta}_{\mathrm{r}}^{H} \widehat{\boldsymbol{\Psi}}_{\mathrm{BR}}^{l} \boldsymbol{\Theta}_{\mathrm{r}}\right)}{M} \\ =\frac{\sum_{l=1}^{L}\left(\mathbf{w}_{k}^{H} \boldsymbol{\Psi}_{\mathrm{BR}}^{l} \mathbf{w}_{k}\right)\left(\boldsymbol{\vartheta}_{\mathrm{r}}^{T} \mathbf{\Xi}^{T}\left(\left(\widehat{\Psi}_{\mathrm{BR}}^{l}\right)^{T} \otimes\left(\boldsymbol{\Omega}_{\mathrm{rw}}^{H} \boldsymbol{\Omega}_{\mathrm{rw}}\right)\right) \boldsymbol{\Xi} \boldsymbol{\vartheta}_{\mathrm{r}}^{*}\right)}{M}, \end{array} limM→∞M∥Φ(wk⊗Θr)ΩrwHg∗∥22=limM→∞MTr(gTΩrw(wk⊗Θr)HΦHΦ(wk⊗Θr)ΩrwHg∗)→(a)MTr(ΩrwHΩrw(wk⊗Θr)HΦHΦ(wk⊗Θr))=(b)MTr(∑l=1L(wkHΨBRlwk)⊗(ΩrwHΩrwΘrHΨ BRlΘr))=(c)M∑l=1L(wkHΨBRlwk)Tr(ΩrwHΩrwΘrHΨ BRlΘr)=M∑l=1L(wkHΨBRlwk)(ϑrTΞT((Ψ BRl)T⊗(ΩrwHΩrw))Ξϑr∗),
具体推导过程在论文Large System Performance of Linear Multiuser Receivers in Multipath Fading Channels中
其中步骤(a)的推导来自于:

相关文章:

渐进推导中常用的一些结论
标题很帅 STAR-RIS Enhanced Joint Physical Layer Security and Covert Communications for Multi-antenna mmWave Systems文章末尾的一个推导。 lim M → ∞ ∥ Φ ( w k ⊗ Θ r ) Ω r w H g ∗ ∥ 2 2 M lim M → ∞ Tr ( g T Ω r w ( w k ⊗ Θ r ) H Φ H Φ…...

网络安全等级保护V2.0测评指标
网络安全等级保护(等保V2.0)测评指标: 1、物理和环境安全 2、网络和通信安全 3、设备和计算安全 4、应用和数据安全 5、安全策略和管理制度 6、安全管理机构和人员 7、安全建设管理 8、安全运维管理 软件全文档获取:点我获取 1、物…...

java中list的addAll用法详细实例?
List 的 addAll() 方法用于将一个集合中的所有元素添加到另一个 List 中。下面是一个详细的实例,展示了 addAll() 方法的使用: java Copy code import java.util.ArrayList; import java.util.List; public class AddAllExample { public static v…...
关于学习计算机的心得与体会
也是隔了一周没有发文了,最近一直在准备期末考试,后来想了很久,学了这么久的计算机,这当中有些收获和失去想和各位正在和我一样在学习计算机的路上的老铁分享一下,希望可以作为你们碰到困难时的良药。先叠个甲…...
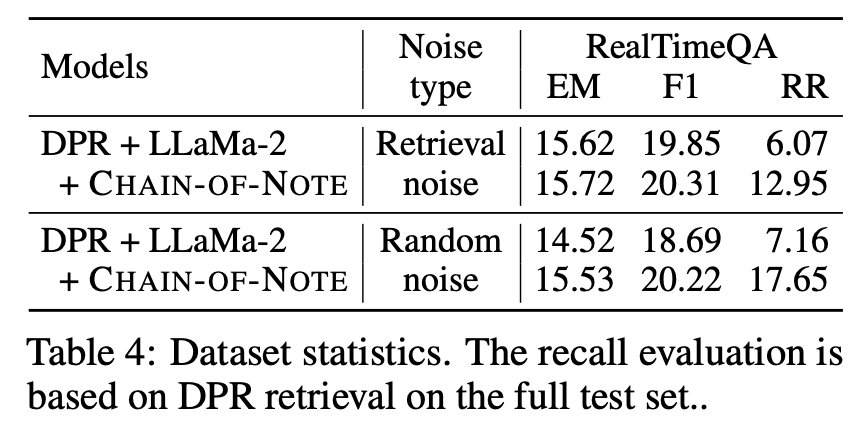
LLM之RAG理论(一)| CoN:腾讯提出笔记链(CHAIN-OF-NOTE)来提高检索增强模型(RAG)的透明度
论文地址:https://arxiv.org/pdf/2311.09210.pdf 检索增强语言模型(RALM)已成为自然语言处理中一种强大的新范式。通过将大型预训练语言模型与外部知识检索相结合,RALM可以减少事实错误和幻觉,同时注入最新知识。然而&…...
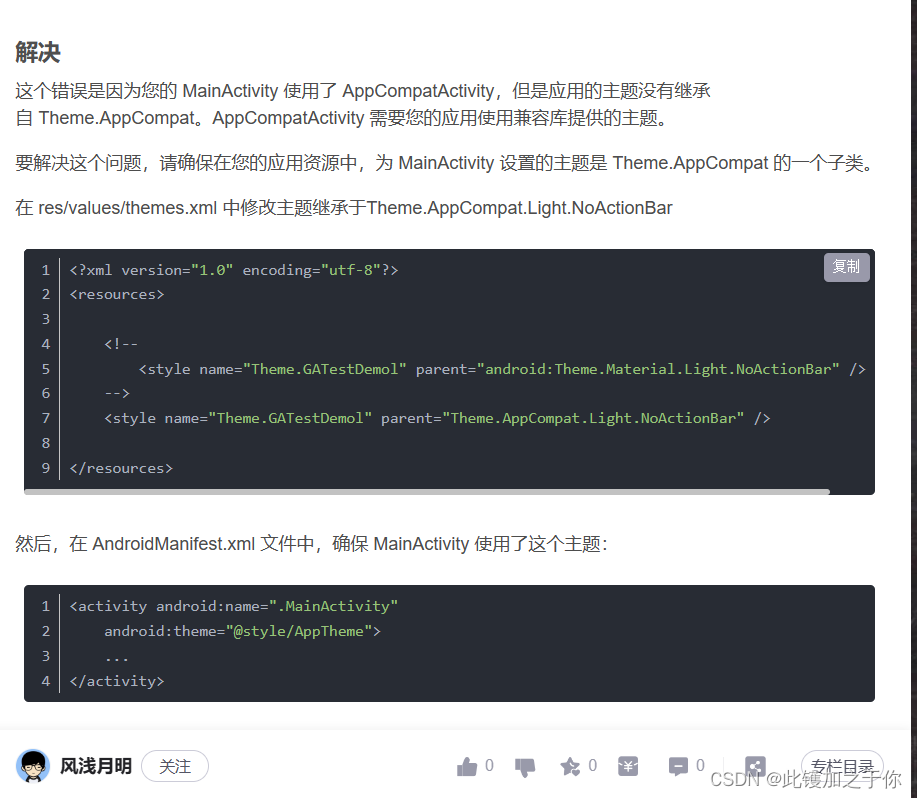
Android studio:打开应用程序闪退的问题2.0
目录 找到问题分析问题解决办法 找到问题 老生常谈,可能这东西真的很常见吧,在之前那篇文章中 linkhttp://t.csdnimg.cn/UJQNb 已经谈到了关于打开Androidstuidio开发的软件后明明没有报错却无法运行(具体表现为应用程序闪退的问题ÿ…...

Spring IoC如何存取Bean对象
小王学习录 IoC(Inversion of Control)1. 什么是IoC2. 什么是Spring IoC3. 什么是DI4. Spring IoC的作用 存储Bean对象1. 创建Bean2. 将Bean注册到Spring中. 取Bean对象.1. 获取Spring上下文信息使用ApplicationContext和BeanFactory的区别 2. 获取指定Bean对象 IoC(Inversion …...

【开源】基于Vue.js的实验室耗材管理系统
文末获取源码,项目编号: S 081 。 \color{red}{文末获取源码,项目编号:S081。} 文末获取源码,项目编号:S081。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 耗材档案模块2.2 耗材入库模块2.3 耗…...
Datawhale聪明办法学Python(task2Getting Started)
一、课程基本结构 课程开源地址:课程简介 - 聪明办法学 Python 第二版 章节结构: Chapter 0 安装 InstallationChapter 1 启航 Getting StartedChapter 2 数据类型和操作 Data Types and OperatorsChapter 3 变量与函数 Variables and FunctionsChapte…...
量化交易怎么操作?量化软件怎么选择比较好?(散户福利,建议收藏)
一:量化的具体操作步骤是什么呢?1. 数据获取:索取和收集金融市场数据。 2. 策略制定:制定数量交易策略,这包括制定投资目标、建立交易规则和风险控制机制等,这个过程需要不断优化和更新。 3. 编写算法&am…...
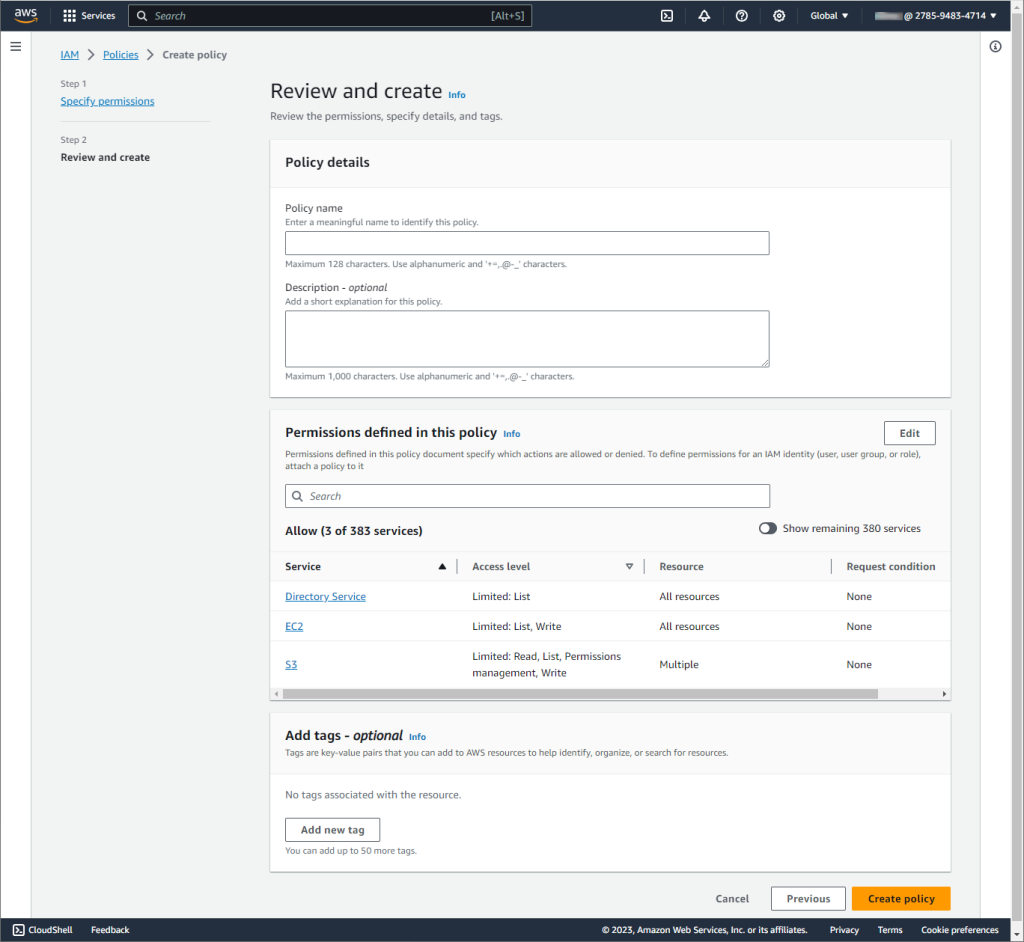
什么是 AWS IAM?如何使用 IAM 数据库身份验证连接到 Amazon RDS(上)
驾驭云服务的安全环境可能很复杂,但 AWS IAM 为安全访问管理提供了强大的框架。在本文中,我们将探讨什么是 AWS Identity and Access Management (IAM) 以及它如何增强安全性。我们还将提供有关使用 IAM 连接到 Amazon Relational Database Service (RDS…...
Python从入门到精通七:Python函数进阶
函数多返回值 学习目标: 知道函数如何返回多个返回值 问: 如果一个函数如些两个return (如下所示),程序如何执行? 答:只执行了第一个return,原因是因为return可以退出当前函数,导致return下方的代码不执…...
uniapp踩坑之项目:使用过滤器将时间格式化为特定格式
利用filters过滤器对数据直接进行格式化,注意:与method、onLoad、data同层级 <template><div><!-- orderInfo.time的数据为:2023-12-12 12:10:23 --><p>{{ orderInfo.time | formatDate }}</p> <!-- 2023-1…...
webpack学习-2.管理资源
webpack学习-2.管理资源 1.这章要干嘛2.加载css注意顺序! 3.总结 1.这章要干嘛 管理资源,什么意思呢?管理什么资源?项目中经常会 导入各种各样的css文件,图片文件,字体文件,数据文件等等&#…...

658. 找到 K 个最接近的元素
658. 找到 K 个最接近的元素 Java代码:滑窗 class Solution {public List<Integer> findClosestElements(int[] arr, int k, int x) {List<Integer> list new ArrayList<>();for (int i 0; i < arr.length; i) {arr[i] arr[i] - x;}for(i…...

十二、MapReduce概述
1、MapReduce (1)采用框架 MapReduce是“分散——>汇总”模式的分布式计算框架,可供开发人员进行相应计算 (2)编程接口: ~Map ~Reduce 其中,Map功能接口提供了“分散”的功能ÿ…...

shell条件测试
目录 1.1.用途 1.2.基本语法 1.2.1.格式: 1.2.2.例 1.3 文件测试 1.4.整数测试 1.4.1.作用 1.4.2.操作符 1.4.3.示例: 1.5.逻辑操作符 1.5.1.符号 1.5.2.例: 1.6.命令分隔符 1.1.用途 为了能够正确处理Shell程序运行过程中遇到的各种情况&am…...

python在线读取传奇列表,并解析为需要的JSON格式
python在线读取传奇列表,并解析为需要的JSON格式,以下为传奇中使用的TXT列表格式, [Server] ; 使用“/”字符分开颜色,也可以不使用颜色,支持以前的旧格式,只有标题和服务器标题支持颜色 ; 标题/颜色代码(0-255)|服务器标题/颜色代码(0-255)|服务器名称|服务器IP|服务器端…...

【docker 】 安装docker(centOS7)
官网 docker官网 github源码 官网 在CentOS上安装Docker引擎 官网 在Debian上安装Docker引擎 官网 在 Fedora上安装Docker引擎 官网 在ubuntu上安装Docker引擎 官网 在RHEL (s390x)上安装Docker引擎 官网 在SLES上安装Docker引擎 最完善的资料都在官网。 卸载旧版本 …...

智能网联汽车场景数据图像标注要求及方法
智能网联汽车场景数据图像标注要求及方法 1 范围 本标准规定了智能网联汽车场景数据图像中交通参与者、交通信号灯、交通标志、交通标线、可行驶区域、光照条件、遮挡截断情况7类元素的标注要求及方法。 本标准适用于智能网联汽车图像数据标注。 2 规范性引…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
