带你了解“函数递归”
目录
1. 什么是递归?
2. 函数递归的必要条件
2.1 接收一个整型值(无符号),按照顺序打印它的每一位。
代码如下:
2.2 编写一个函数,不用临时变量求字符串长度
代码如下:
2.3 递归与迭代
2.3.1 求n!(不考虑溢出)
代码如下:
2.3.2 求第n个斐波那契数(不考虑溢出)
代码如下
1. 什么是递归?
- 程序调用自身的编程技巧称为i而递归(recursion)。
- 递归作为一种算法再程序设计语言中广泛应用。一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为为一个与原问题相似的规模较小的问题来求解,递归策略只需要只需要少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。
- 递归的主要思考方式在于:大事化小
现在看这个概念可能有一点抽象,我们举一个最简单的例子:
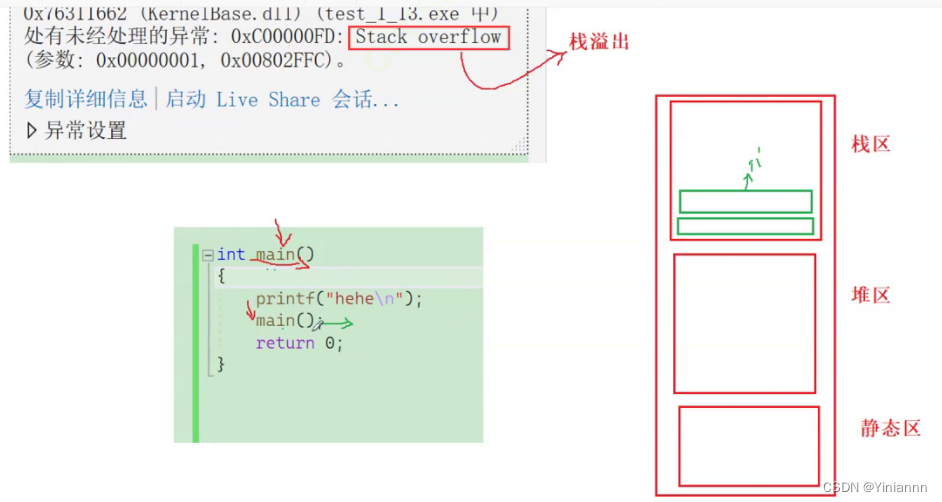
int main() {printf("LOVE YOU\n");main();//函数在里面自己调用自己就是递归return 0; }但是这个代码还是有一定的问题的:它会栈溢出。
内存分为栈区、堆区和静态区,我们知道当我们调用函数时,它会在栈区申请空间。但是我们这个函数是无限循环的,它一直调用main函数,直到栈区没有空间了,它才停止。
当然,这只是一个例子,我们在写代码的时候,不会这样写。
2. 函数递归的必要条件
- 存在限制条件,当满足这个限制条件的时候,递归便不再继续。
- 每次递归调用之后越来越接近这个限制条件。
2.1 接收一个整型值(无符号),按照顺序打印它的每一位。
例如:
输入:1234,输出:1 2 3 4.
我们可以先看看能不能计算:
1234%10=4(打印)
1234/10=123
123%10=3(打印)
123/10=12
12%10=2(打印)
12/10=1
1%10=1(打印)
这样虽然可以计算,但是顺序错了,用刚刚学的递归就可以解决(我们这里的限制条件是:只剩下个位数后不需要递归)
代码如下:
#include <stdio.h>void Print(unsigned int n) {if (n > 9){Print(n / 10);}printf("%d ", n % 10); }int main() {unsigned int num = 0;scanf("%u", num);Print(num);return 0; }代码可能有些难理解,我们看下面的图:

递归的递是递推,就是上面的绿色箭头
递归的归是回归,就是上面的红色箭头
2.2 编写一个函数,不用临时变量求字符串长度
乍一看这个问题好像很难,没关系,我们先减小难度。编写一个函数求字符串长度。

很简单对吧,我们再加一点难度:用调用函数写。
arr[10]="a b c d e f \0 _ _ _"
- 首先我们要知道数组 arr 的指针就是第一个字母 a 的指针
- 当我们的指针 str 指向 a 时,我们记为 1 ,然后 str++,指针向下走指向 b ……最后当 str = ' \0 ' 时停止计数,所以这是一个循环。
- 定义一个计数变量 count ,每当进入循环 count++;str++;
- 当循环结束,返回 count 。
#include <stdio.h>
#include <string.h>int my_strlen(char* str)
{int count = 0;while (*str != '\0'){count++;str++;}return count;
}int main()
{char arr[10] = "abcdef";int len = my_strlen(arr);printf("%d\n", len);return 0;
}理解之后我们进一步改良,使其符合题目:
题目不需要临时变量,count就不能用了。但是,我们还是之前的思路,只是用递归的方法:
首先,递归要有一个限制条件:指针不为 ' \0 '。满足这个条件后,指针+1,但是我们还要计数,直接返回的时候+1。否则,也就是说如果一开始就是 ' \0 ' ,那我们就直接返回0。
代码如下:
#include <stdio.h>
#include <string.h>int my_strlen(char* str)
{if (*str != '\0'){return 1 + my_strlen(str + 1);}elsereturn 0;
}int main()
{char arr[10] = "abcdef";int len = my_strlen(arr);printf("%d\n", len);return 0;
}2.3 递归与迭代
循环是迭代的一种:
- 循环(loop),指的是在满足条件的情况下,重复执行同一段代码。比如,while语句。 循环则技能对应集合,列表,数组等,也能对执行代码进行操作。
- 迭代(iterate),指的是按照某种顺序逐个访问列表中的每一项。比如,for语句。 迭代只能对应集合,列表,数组等。不能对执行代码进行迭代。
2.3.1 求n!(不考虑溢出)
我们以前也写过求 n! :
- 主函数:输入n,定义ret接收调用函数 fac 的返回值,打印 ret 。
- 调用函数:定义 i=1 和 ret=1 ,循环出 1 - n 的数,让 i <= n ,不断让 ret = ret * i 。
#include <stdio.h>int fac(int n) {int i = 0;int ret = 1;for (i = 1; i <= n; i++){ret = ret * i;}return ret; }int main() {int n = 0;scanf("%d\n", &n);int ret=fac(n);printf("%d\n", ret);return 0; }
除了这种循环(迭代)的写法,我们还可以改良一下,用递归写:fac(n) = n * fac(n-1)
- 当 n <= 1 时,返回1
- 当 n > 1 时,返回 n * fac(n-1)
代码如下:
int fac(int n)
{if (n <= 1)return 1;elsereturn n * fac(n - 1);}int main()
{int n = 0;scanf("%d", &n);int ret = fac(n);printf("%d", ret);return 0;
}2.3.2 求第n个斐波那契数(不考虑溢出)
斐波那契数列指的是这样一个数列:1,1,2,3,5,8,13,21,34,55,89...
- 这个数列从第3项开始,每一项都等于前两项之和。
- 在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)
要写这个函数,首先我们要知道前两个数字,第三项开始就是前两项之和,我们只需要计算到 n * (n-1) 。
当 n <= 2 ,斐波那契数是 1 ;
当 n > 2 ,斐波那契数是前两项之和;
int Fib(int n)
{if (n <= 2)return 1;elsereturn Fib(n - 1) + Fib(n-2);
}int main()
{int n = 0;scanf("%d", &n);int ret = Fib(n);printf("%d", ret);return 0;
}虽然这种方法可行,但是过程非常繁琐,当你输入的数字较大时需要递归很多次,有很多重复大量的计算。
递归虽然可行,但是有没有其他的更简单的方法,不用递归,直接从前往后算:前两个相加等于第三个;用迭代的方式计算:
代码如下:
int Fib(int n) {int a = 1;int b = 1;int c = 1;while (n>=3){c = a + b;a = b;b = c;n--;}return c; } int main() {int n = 0;scanf("%d", &n);int ret = Fib(n);printf("%d", ret);return 0; }
相关文章:

带你了解“函数递归”
目录 1. 什么是递归? 2. 函数递归的必要条件 2.1 接收一个整型值(无符号),按照顺序打印它的每一位。 代码如下: 2.2 编写一个函数,不用临时变量求字符串长度 代码如下: 2.3 递归与迭代 …...
网络资源面经2
文章目录Kafka 原理,数据怎么平分到消费者生产者分区消费者分区Flume HDFS Sink 小文件处理Flink 与 Spark Streaming 的差异,具体效果Spark 背压机制具体实现原理Yarn 调度策略Spark Streaming消费方式及区别Zookeeper 怎么避免脑裂,什么是脑…...
4年经验来面试20K的测试岗,一问三不知,我还真不如去招应届生。
公司前段缺人,也面了不少测试,结果竟然没有一个合适的。一开始瞄准的就是中级的水准,也没指望来大牛,提供的薪资在10-20k,面试的人很多,但平均水平很让人失望。看简历很多都是4年工作经验,但面试…...

K8S搭建NACOS集群踩坑问题
一、NACOS容器启动成功无法访问现象描述:通过K8S的statefulset启动,通过NodePort暴露不能在外网访问,只能在MASTER主节点访问。yaml配置:apiVersion: apps/v1 kind: StatefulSet metadata:name: nacos-${parameters.nameSpace}-dm…...

怎么避免计算机SCI论文的重复率过高? - 易智编译EaseEditing
论文成稿前 在撰写阶段就避免重复:在撰写阶段就避免文章中的重复内容,可以减少后期修改的工作量。 在写作前,可以制定良好的计划和大纲,规划好文章的结构和内容,从而减少重复内容。 加强对相关文献的阅读 为了避免自己…...

uni-app路由拦截
新建一个auth.js /** * description 权限存储函数 */ const authorizationKey Authorization export function getAuthorization() { return uni.getStorageSync(authorizationKey) } export function setAuthorization(authorization) { return uni.setStorageSync(aut…...
如何使用固态继电器实现更高可靠性的隔离和更小的解决方案尺寸
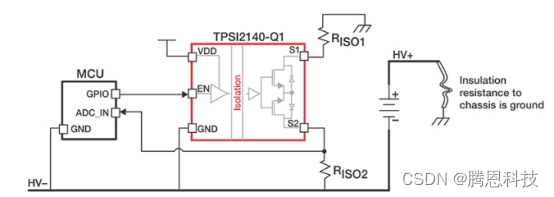
自晶体管发明之前,继电器就已被用作开关。从低压信号安全控制高压系统的能力,如隔离电阻监控,对于许多汽车系统的开发是必要的。虽然机电继电器和接触器的技术多年来有所改进,但设计人员要实现其终身可靠性和快速开关速度以及低噪…...

【YOLOv8/YOLOv7/YOLOv5系列算法改进NO.56】引入Contextual Transformer模块(sci期刊创新点之一)
文章目录前言一、解决问题二、基本原理三、添加方法四、总结前言 作为当前先进的深度学习目标检测算法YOLOv8,已经集合了大量的trick,但是还是有提高和改进的空间,针对具体应用场景下的检测难点,可以不同的改进方法。此后的系列…...

深圳大学计软《面向对象的程序设计》实验3 指针2
A. 月份查询(指针数组) 题目描述 已知每个月份的英文单词如下,要求创建一个指针数组,数组中的每个指针指向一个月份的英文字符串,要求根据输入的月份数字输出相应的英文单词 1月 January 2月 February 3月 March …...

【基于机器学习的推荐系统项目实战-2】项目介绍与技术选型
本节目录一、项目介绍1.1 采用的数据源1.2 Concrec架构技术选型1.3 Sprak介绍1.4 Flink1.5 TensorFlow一、项目介绍 1.1 采用的数据源 Kaggle Anime Recommendations Dataset。 其中的动漫数据源自myanimelist.net。 1.2 Concrec架构技术选型 数据预处理模块:汇总…...

对称锥规划:锥与对称锥
文章目录对称锥规划:锥与对称锥锥的几何形状常用的指向锥Nonnegative Orthant二阶锥半定锥对称锥对称锥的平方操作对称锥的谱分解对称锥的自身对偶性二阶锥规划SOCP参考文献对称锥规划:锥与对称锥 本文主要讲锥与对称锥的一些基本概念。 基础预备&…...

4.基于Label studio的训练数据标注指南:情感分析任务观点词抽取、属性抽取
情感分析任务Label Studio使用指南 1.基于Label studio的训练数据标注指南:信息抽取(实体关系抽取)、文本分类等 2.基于Label studio的训练数据标注指南:(智能文档)文档抽取任务、PDF、表格、图片抽取标注等…...
算法拾遗二十五之暴力递归到动态规划五
算法拾遗二十七之暴力递归到动态规划七题目一【数组累加和最小的】题目二什么暴力递归可以继续优化暴力递归和动态规划的关系面试题和动态规划的关系如何找到某个问题的动态规划方式面试中设计暴力递归的原则知道了暴力递归的原则 然后设计常见的四种尝试模型如何分析有没有重复…...

Linux进程的创建结束类系统调用总结
tags: Linux OS Syscall C 写在前面 总结一下Linux系统的进程创建/终止/等待等系统调用, 参考: Linux/Unix系统编程手册. 下面主要给出例子, 关于函数原型可以参考书中或者man 2 syscall(例如man 2 fork). 测试环境: Ubuntu 20.04 x86_64 gcc-9 进程创建: fork() 用于创建…...

Git分支的合并策略有哪些?Merge和Rebase有什么区别?关于Merge和Rebase的使用建议
Git分支的合并策略有哪些?Merge和Rebase有什么区别?关于Merge和Rebase的使用建议1. 关于Git的一些基本原理1.1 Git的工作流程原理2. Git的分支合并方式浅析2.1 分支是什么2.2 分支的合并策略2.2.1 Three-way-merge(三向合并原理)2…...
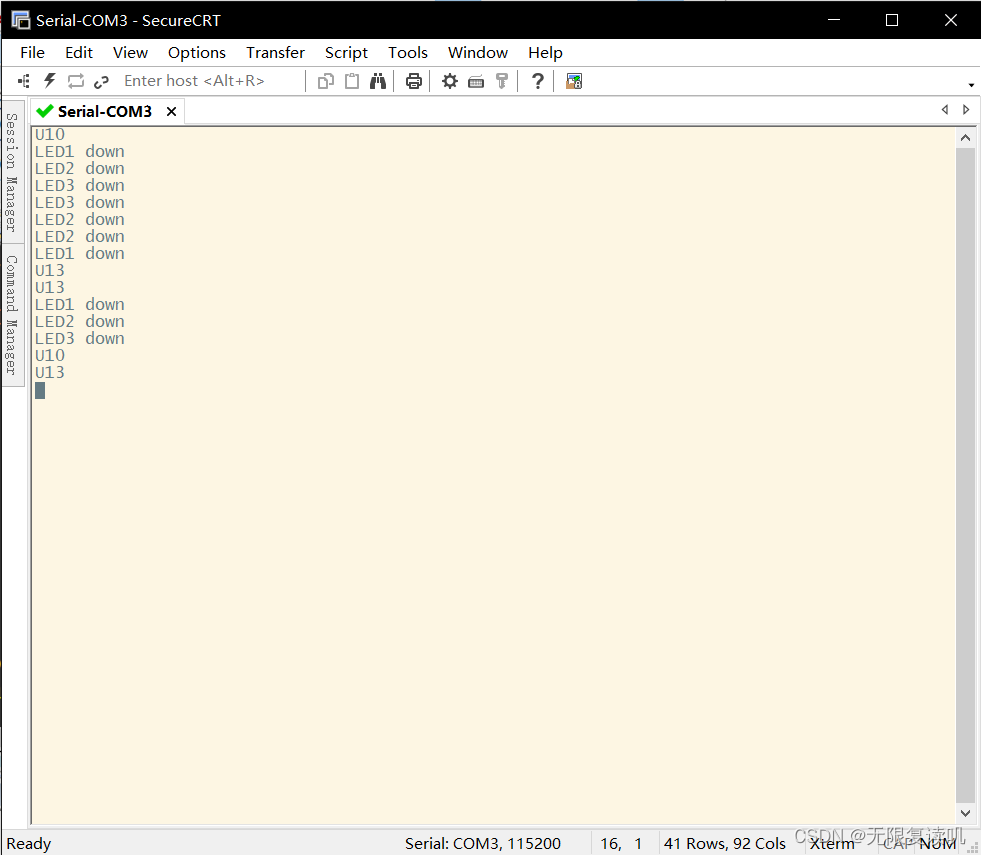
2022-2-23作业
一、通过操作Cortex-A7核,串口输入相应的命令,控制LED灯进行工作 1.例如在串口输入led1on,开饭led1灯点亮 2.例如在串口输入led1off,开饭led1灯熄灭 3.例如在串口输入led2on,开饭led2灯点亮 4.例如在串口输入led2off,开饭led2灯熄灭 5.例如在串口输…...
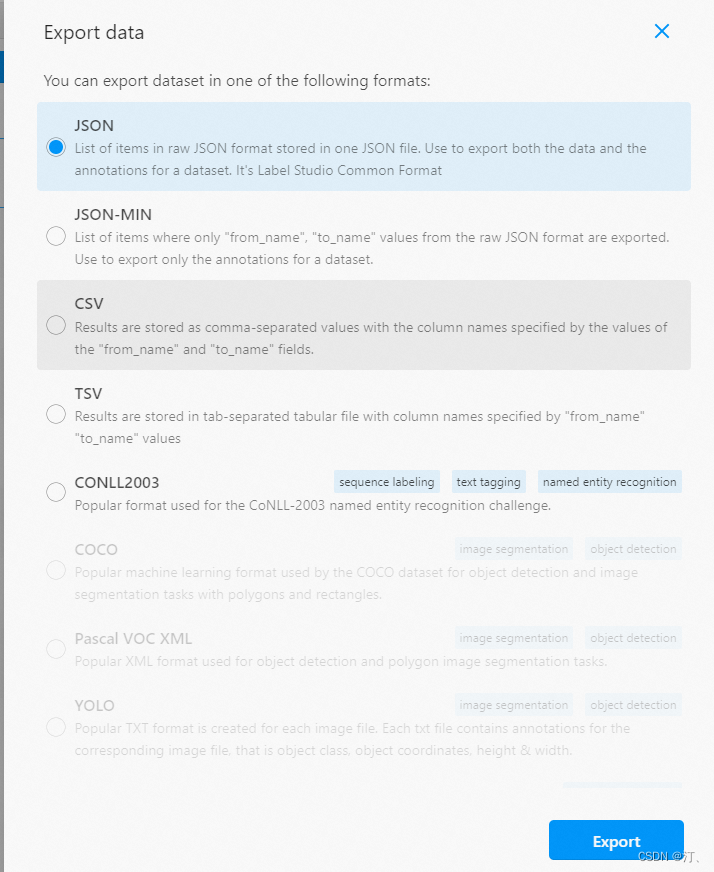
1.基于Label studio的训练数据标注指南:信息抽取(实体关系抽取)、文本分类等
文本抽取任务Label Studio使用指南 1.基于Label studio的训练数据标注指南:信息抽取(实体关系抽取)、文本分类等 2.基于Label studio的训练数据标注指南:(智能文档)文档抽取任务、PDF、表格、图片抽取标注等…...

“高退货率”标签引热议,亚马逊跨境电商是好是坏?
在多数卖家不知情的情况下,亚马逊“高退货率”标签上线,该消息已被官方证实,目的是为了践行以客户为中心的理念和推动卖家提升服务。 官方确认上线“高退货率”标签 近期,有亚马逊卖家发现产品详情页出现了“高退货率”标签&…...

Pinia2
一、入门案例 1、安装 npm i pinia -S 2、注册插件 //main.ts import { createPinia } from pinia app.use(createPinia()) 3、创建store/countStore.ts import { defineStore } from "pinia"; const useCounterStore defineStore(counterStore,{ state(){ return{…...
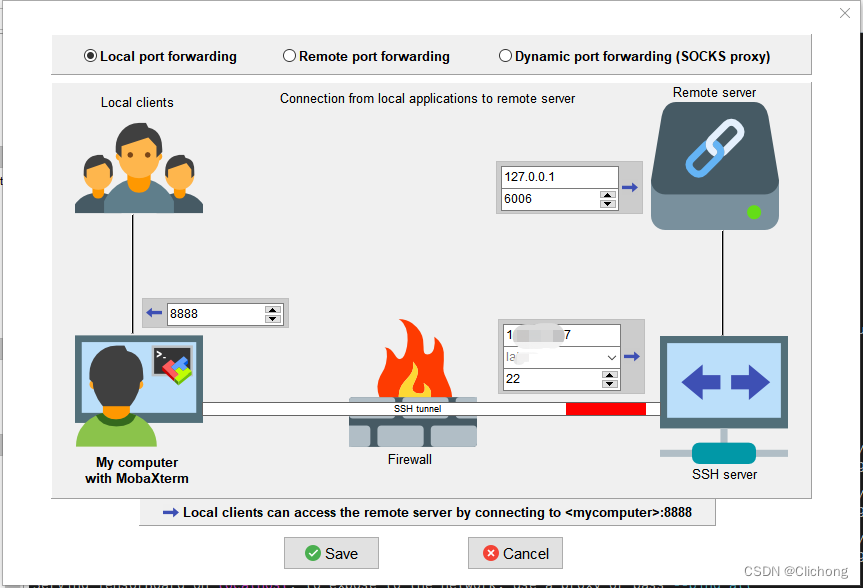
服务器配置 | 在Windows本地打开服务器端Tensorboard结果
文章目录方法1:直接cmd使用ssh登录远程服务器方法2:利用Xshell设置本地端口进行监听方法3:利用MobaXterm设置本地端口监听这里介绍三个方法,在在Windows本地打开服务器端Tensorboard结果 方法1:直接cmd使用ssh登录远程…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...

Qt Quick Dialogs模块功能及架构
Qt Quick Dialogs 是 Qt Quick 的一个附加模块,提供了一套用于创建和使用系统对话框的 QML 类型。在 Qt 6.0 中,这个模块经过了重构和增强。 一、主要功能和特点 1. 对话框类型 Qt Quick Dialogs 在 Qt 6.0 中提供了以下标准对话框类型: …...

C语言指针与数组sizeof运算深度解析:从笔试题到内存原理
前两天跟着数组指针的教程: // #self 视频里的笔试题 !!!vipint b12[3][4] {0};printf("%ld \n", sizeof(b12[0]));printf("%ld \n", sizeof(*b12));printf("%ld \n", sizeof(*(b12 1)));printf("%ld \n", sizeof(*(&am…...

Mac版Visual Studio Code Copilot 无法使用的解决方法
1 app文件夹删除Visual Studio Code 2 终端里面 输入以下指令,删除各种缓存 rm -fr ~/Library/Preferences/com.microsoft.VSCode.helper.plist rm -fr ~/Library/Preferences/com.microsoft.VSCode.plist rm -fr ~/Library/Caches/com.microsoft.VSCode rm -f…...