Java 数据结构篇-用数组、堆实现优先级队列
🔥博客主页: 【小扳_-CSDN博客】
❤感谢大家点赞👍收藏⭐评论✍


文章目录
1.0 优先级队列说明
2.0 用数组实现优先级队列
3.0 无序数组实现优先级队列
3.1 无序数组实现优先级队列 - 入队列 offer(E value)
3.2 无序数组实现优先级队列 - 出队列 poll()
3.3 无序数组实现优先级队列 - 查看队列中优先级最大的元素 peek()
3.4 无序数组实现优先级队列 - 判断是否为空队列
3.5 无序数组实现优先级队列 - 判断是否为满队列
3.6 无序数组实现优先级队列完整代码
4.0 有序数组实现优先级队列
4.1 有序数组实现优先级队列 - 入队列 offer(E value)
4.2 有序数组实现有序队列 - 出队列 poll()
4.3 有序数组实现有序队列 - 查看优先级最大的元素 peek()
4.4 有序数组实现优先级队列 - 判断队列是否为空
4.5 有序数组实现优先级队列 - 判断队列是否为满队列
4.6 有序数组实现优先级队列完整代码
5.0 大顶堆实现优先级队列
5.1 堆实现优先级队列 - 入队列 offer(E value)
5.2 堆实现优先级队列 - 出队列 poll()
5.3 堆实现优先级队列 - 查看优先级最大的元素 peek()
5.4 堆实现优先级队列 - 判断该队列是否为空
5.5 堆实现优先级队列 - 判断该队列是否为满队列
5.6 堆实现优先级队列完整代码
1.0 优先级队列说明
优先级队列是一种特殊的队列,其中每个元素都有一个优先级。在优先级队列中,具有最高优先级的元素首先被移除。这与普通队列不同,普通队列是先进先出(FIFO)的,而优先级队列则是按照优先级来确定元素的出队顺序。
优先级队列通常用于需要按照优先级处理元素的场景,比如任务调度、事件处理等。它可以使用不同的数据结构来实现,最常见的是使用堆(heap)来实现优先队列。堆是一种特殊的树形数据结构,它可以快速找到并移除具有最高(或最低)优先级的元素。
优先级队列的常见操作包括插入元素、移除具有最高优先级的元素、查看具有最高优先级的元素等。实现优先级队列的常见算法包括插入时的堆调整、移除最高优先级元素后的堆调整等。
2.0 用数组实现优先级队列
可以使用数组来实现优先级队列,一种简单的实现方式是使用数组来存储元素,并且按照优先级顺序来维护数组。
用数组实现优先级队列可分为两种:无序数组实现、有序数组实现。
3.0 无序数组实现优先级队列
可以直接简单粗暴来说,无序数组就是插入元素的时候不按照优先级进行排序,而出队列的时候,严格按照优先级大小进行出队列。
首先,需要实现队列中的接口。比如:入队列、出队列等。
接口代码如下:
public interface Queue<E> {/*** 入队操作*/boolean offer(E value);/*** 出队操作*/E poll();/*** 查看队头元素*/E peek();/*** 判断是否为空队列*/boolean isEmpty();/*** 判断是否为满队列*/boolean isFull(); }
再接着,设置优先级元素。
代码如下:
public interface Priority {int priority();}public class Entry implements Priority{String string;int priority;public Entry(String string, int priority) {this.string = string;this.priority = priority;}@Overridepublic int priority() {return priority;}@Overridepublic String toString() {return "Entry{" +"string='" + string + '\'' +", priority=" + priority +'}';} }该设置的优先级元素需要实现 priority 接口,返回当前优先级的大小。
成员变量有 Priority[] arr 自定义大小的数组、size 标记当前元素的个数。
代码如下:
public class UnorderedPriorityQueue<E extends Priority> implements Queue<E> {private Priority[] arr;private int size;public UnorderedPriorityQueue(int capacity) {arr = new Priority[capacity];}}
3.1 无序数组实现优先级队列 - 入队列 offer(E value)
由于用无序数组实现,元素可直接在数组尾部入队列。
代码如下:
@Overridepublic boolean offer(E value) {if (isFull()) {return false;}arr[size++] = value;return true;}注意:在入队前,需要判断是否为满队列。入队完后,需要进行 size++ 。
3.2 无序数组实现优先级队列 - 出队列 poll()
根据元素的优先级大小进行出队列,首先需要遍历数组找到索引为 i 处优先级最大的元素。一般有两种情况:
第一种情况:在索引为 i == size - 1 处找到优先级最大的元素,此时只需要将 size-- ,然后将其引用置为空 arr[size] = null 。
第二种情况:不在索引为 i != size - 1 处找到优先级最大的元素。那么需要将索引为 i 的元素被 i + 1 处的元素进行覆盖,长度为:size - 1 - i 。
代码如下:
@Overridepublic E poll() {if (isEmpty()) {return null;}//先找到优先级大的点int j = 0;for (int i = 1; i < size; i++) {if (arr[j].priority() < arr[i].priority()) {j = i;}}E ret = (E)arr[j];if (j < size - 1) {System.arraycopy(arr,j+1,arr,j,size - 1 - j);}size--;arr[size] = null;return ret;}最后需要返回优先级最大的元素,在被置为 null 之前将其进行保存。每次出队完毕,后需要进行 size-- 、置为 null 。
3.3 无序数组实现优先级队列 - 查看队列中优先级最大的元素 peek()
相比与出队列,找到了优先级最大的元素后,不需要进行删除该优先级最大的元素。
代码如下:
@Overridepublic E peek() {if (isEmpty()) {return null;}//先找到优先级大的点int j = 0;for (int i = 1; i < size; i++) {if (arr[j].priority() < arr[i].priority()) {j = i;}}E ret = (E)arr[j];return ret;}注意:在查看元素之前需要先判断是否为空队列。
3.4 无序数组实现优先级队列 - 判断是否为空队列
若 size == 0 ,则为空队列;若不是,则不为空。
代码如下:
@Overridepublic boolean isEmpty() {return size == 0;}
3.5 无序数组实现优先级队列 - 判断是否为满队列
若 size == arr.length 时,则为满队列;若不相等,则不为满。
代码如下:
@Overridepublic boolean isFull() {return size == arr.length;}
3.6 无序数组实现优先级队列完整代码
public class UnorderedPriorityQueue<E extends Priority> implements Queue<E> {private Priority[] arr;private int size;public UnorderedPriorityQueue(int capacity) {arr = new Priority[capacity];}@Overridepublic boolean offer(E value) {if (isFull()) {return false;}arr[size++] = value;return true;}@Overridepublic E poll() {if (isEmpty()) {return null;}//先找到优先级大的点int j = 0;for (int i = 1; i < size; i++) {if (arr[j].priority() < arr[i].priority()) {j = i;}}E ret = (E)arr[j];if (j < size - 1) {System.arraycopy(arr,j+1,arr,j,size - 1 - j);}size--;arr[size] = null;return ret;}@Overridepublic E peek() {if (isEmpty()) {return null;}//先找到优先级大的点int j = 0;for (int i = 1; i < size; i++) {if (arr[j].priority() < arr[i].priority()) {j = i;}}E ret = (E)arr[j];return ret;}@Overridepublic boolean isEmpty() {return size == 0;}@Overridepublic boolean isFull() {return size == arr.length;} }
4.0 有序数组实现优先级队列
相对于无序数组优先级队列来说,有序数组实现优先级队列入队列操作需要按照优先级大小进行插入,而出队列操作直接在索引为 size - 1 处直接获取该最大优先级元素。
首先,同样的,需要实现队列中的接口。比如:入队列、出队列等。
接口代码如下:
public interface Queue<E> {/*** 入队操作*/boolean offer(E value);/*** 出队操作*/E poll();/*** 查看队头元素*/E peek();/*** 判断是否为空队列*/boolean isEmpty();/*** 判断是否为满队列*/boolean isFull(); }
再接着,设置优先级元素。
代码如下:
public class Entry implements Priority{String string;int priority;public Entry(String string, int priority) {this.string = string;this.priority = priority;}@Overridepublic int priority() {return priority;}@Overridepublic String toString() {return "Entry{" +"string='" + string + '\'' +", priority=" + priority +'}';} }
成员变量有 Priority[] arr 自定义大小的数组、size 标记当前元素的个数。
代码如下:
public class OrderedPriorityQueue<E extends Priority> implements Queue<E>{private Priority[] arr;private int size;public OrderedPriorityQueue(int capacity) {arr = new Priority[capacity];}}
4.1 有序数组实现优先级队列 - 入队列 offer(E value)
使用有序数组实现优先级入队列,在入队列之前从后往前遍历数组,找到优先级小于入队列的元素优先级,找到即可插入其中。
代码如下:
@Overridepublic boolean offer(E value) {if (isFull()) {return false;}//先找到优先级比value的优先级大的索引int i = size - 1;while (i >= 0 && arr[i].priority() > value.priority()) {arr[i+1] = arr[i];i--;}arr[i+1] = value;size++;return true;}考虑一种情况,若 size == 0 时,为空队列的时候,该代码有无错误?
答案是:没有问题的,当 size == 0 时, 则 i = 0 - 1,i = -1 , 此时不会进入循环直接跳到 arr[i + 1] 处,所以,在这种情况下,该代码没有问题。
4.2 有序数组实现有序队列 - 出队列 poll()
这就相对于有序数组入队列来说比较简单了,直接在索引为 i = size - 1 处,得到优先级最大的元素,然后将 size-- ,再接着 arr[size] 置为 null 。
代码如下:
@Overridepublic E poll() {if (isEmpty()) {return null;}E str = (E)arr[size - 1];size--;arr[size] = null;return str;}注意:需要记录优先级最大的元素并且返回。在出队列之前需要判断该队列是否为空队列。
4.3 有序数组实现有序队列 - 查看优先级最大的元素 peek()
先判断该队列是否为空队列,若不是,直接返回该数组索引为 size - 1 处的元素即可。
代码如下:
@Overridepublic E peek() {if (isEmpty()) {return null;}E str = (E)arr[size - 1];return str;}
4.4 有序数组实现优先级队列 - 判断队列是否为空
若 size == 0 ,则为空;若不为,则为不空。
代码如下:
@Overridepublic boolean isEmpty() {return size == 0;}
4.5 有序数组实现优先级队列 - 判断队列是否为满队列
若 size == arr.length 时,则为满队列;若不是,则为不满队列。
代码如下:
@Overridepublic boolean isFull() {return size == arr.length;}
4.6 有序数组实现优先级队列完整代码
public class OrderedPriorityQueue<E extends Priority> implements Queue<E>{private Priority[] arr;private int size;public OrderedPriorityQueue(int capacity) {arr = new Priority[capacity];}@Overridepublic boolean offer(E value) {if (isFull()) {return false;}//先找到优先级比value的优先级大的索引int i = size - 1;while (i >= 0 && arr[i].priority() > value.priority()) {arr[i+1] = arr[i];i--;}arr[i+1] = value;size++;return true;}@Overridepublic E poll() {if (isEmpty()) {return null;}E str = (E)arr[size - 1];size--;arr[size] = null;return str;}@Overridepublic E peek() {if (isEmpty()) {return null;}E str = (E)arr[size - 1];return str;}@Overridepublic boolean isEmpty() {return size == 0;}@Overridepublic boolean isFull() {return size == arr.length;} }
5.0 大顶堆实现优先级队列
大顶堆说明:
大顶堆是一种特殊的堆,它是一种完全二叉树,其中每个父节点的值都大于或等于其左右子节点的值。在大顶堆中,根节点的值是整个堆中最大的。
大顶堆可以使用数组来实现,其中堆的根节点存储在数组的第一个位置,然后按照完全二叉树的性质依次存储其他节点。这种实现方式使得大顶堆的父节点和子节点之间可以通过简单的数学关系来计算,从而方便进行堆调整操作。假设 i 不为 0 ,该双亲索引为:(i - 1)/ 2 ;该左孩子为:2 * i + 1;该右孩子为:2 * i + 2 。
首先,需要实现队列中的接口。比如:入队列、出队列等。
接口代码如下:
public interface Queue<E> {/*** 入队操作*/boolean offer(E value);/*** 出队操作*/E poll();/*** 查看队头元素*/E peek();/*** 判断是否为空队列*/boolean isEmpty();/*** 判断是否为满队列* */boolean isFull(); }
再接着,设置优先级元素。
代码如下:
public class Entry implements Priority{String string;int priority;public Entry(String string, int priority) {this.string = string;this.priority = priority;}@Overridepublic int priority() {return priority;}@Overridepublic String toString() {return "Entry{" +"string='" + string + '\'' +", priority=" + priority +'}';} }
成员变量有 Priority[] arr 自定义大小的数组、size 标记当前元素的个数。
代码如下:
public class BigTopPile<E extends Priority> implements Queue<E> {private Priority[] arr;private int size;public BigTopPile(int capacity) {arr = new Priority[capacity];}}
5.1 堆实现优先级队列 - 入队列 offer(E value)
具体思路为:由于是按照优先级大小来存放元素的,所以,需要先比较优先级大小,在适合的位置插入。现在已知 i = size,该双亲为:(i - 1)/ 2 。接下来,需要判断 arr[(i - 1)/ 2] 的优先级于入队列的元素优先级大小,若 arr[(i - 1)/ 2] 的优先级较大,此时该入队列的元素存放的位置为 arr[i] = value ;若 value 的优先级大于当前 arr[(i - 1)/ 2] 时,先将当前 arr[(i - 1)/ 2] 往后放,即 arr[i] = arr[(i - 1)/ 2] 。之后需要继续往上找双亲,将 i = (i - 1) / 2 ,直到 i == 0 或者 value 的优先级小于当前 arr[(i - 1)/ 2] 时,则为 arr[i] = value 。
代码如下:
@Overridepublic boolean offer(E value) {if (isFull()) {return false;}int i = size;int j = (i - 1) / 2;while (i > 0 && arr[j].priority() < value.priority()) {arr[i] = arr[j];i = j;j = (i - 1) / 2;}arr[i] = value;size++;return true;}只要 i == 0 时, j 不能继续往上走了,否则为抛空指针异常。
5.2 堆实现优先级队列 - 出队列 poll()
具体思路为:分为两步。
第一步,将 arr[size - 1] 处的元素交换到 arr[0] 处。
第二步,由于根处的优先级永远都要大于该孩子的优先级,所以,将交换之后的元素进行下潜,即先找到该左右孩子优先级最大的元素,于根元素进行交换,一直往下进行下潜。直到该根元素没有左右孩子或者根元素的优先级都大于该左右孩子的优先级。
代码实现:
非递归实现:
@Overridepublic E poll() {if (isEmpty()) {return null;}E top = (E)arr[0];arr[0] = arr[size - 1];size--;arr[size] = null;int i = 0;while ( (i * 2 + 1) < size && (i * 2 + 2) < size && (arr[i].priority() < arr[i * 2 + 1].priority() || arr[i].priority() < arr[i * 2 + 2].priority() ) ) {int j = 0;if (arr[i * 2 + 1].priority() > arr[i * 2 + 2].priority()) {j = i * 2 + 1;}else if (arr[i * 2 + 1].priority() <= arr[i * 2 + 2].priority()) {j = i * 2 + 2;}E temp = (E)arr[j];arr[j] = arr[i];arr[i] = temp;i = j;}return top;}(i * 2 + 1) < size && (i * 2 + 2) < size 该代码判断的是有无左右孩子元素。
递归实现:
public E poll1() {if (isEmpty()) {return null;}//交换头尾swap(0,size - 1);size--;//置为 nullE ret = (E)arr[size];arr[size] = null;//下潜down(0);return ret;}private void swap(int i, int j) {E t = (E)arr[i];arr[i] = arr[j];arr[j] = t;}private void down(int i) {int left = 2 * i + 1;int right = 2 * i + 2;int max = i;if ( left < size && arr[max].priority() < arr[left].priority()) {max = left;}if (right < size && arr[max].priority() < arr[right].priority()) {max = right;}if (max != i) {swap(max,i);down(max);}}
5.3 堆实现优先级队列 - 查看优先级最大的元素 peek()
先判断该队列是否为空,若不为空,则直接返回堆顶元素即可。
代码如下:
@Overridepublic E peek() {if (isEmpty()) {return null;}return (E)arr[0];}
5.4 堆实现优先级队列 - 判断该队列是否为空
当 size == 0 时,则为空队列。
代码实现:
@Overridepublic boolean isEmpty() {return size == 0;}
5.5 堆实现优先级队列 - 判断该队列是否为满队列
当 size == arr.length 时,则为满队列。
代码实现:
@Overridepublic boolean isFull() {return size == arr.length;}
5.6 堆实现优先级队列完整代码
public class BigTopPile<E extends Priority> implements Queue<E> {private Priority[] arr;private int size;public BigTopPile(int capacity) {arr = new Priority[capacity];}@Overridepublic boolean offer(E value) {if (isFull()) {return false;}int i = size;int j = (i - 1) / 2;while (i > 0 && arr[j].priority() < value.priority()) {arr[i] = arr[j];i = j;j = (i - 1) / 2;}arr[i] = value;size++;return true;}@Overridepublic E poll() {if (isEmpty()) {return null;}E top = (E)arr[0];arr[0] = arr[size - 1];size--;arr[size] = null;int i = 0;while ( (i * 2 + 1) < size && (i * 2 + 2) < size && (arr[i].priority() < arr[i * 2 + 1].priority() || arr[i].priority() < arr[i * 2 + 2].priority() ) ) {int j = 0;if (arr[i * 2 + 1].priority() > arr[i * 2 + 2].priority()) {j = i * 2 + 1;}else if (arr[i * 2 + 1].priority() <= arr[i * 2 + 2].priority()) {j = i * 2 + 2;}E temp = (E)arr[j];arr[j] = arr[i];arr[i] = temp;i = j;}return top;}public E poll1() {if (isEmpty()) {return null;}//交换头尾swap(0,size - 1);size--;//置为 nullE ret = (E)arr[size];arr[size] = null;//下潜down(0);return ret;}private void swap(int i, int j) {E t = (E)arr[i];arr[i] = arr[j];arr[j] = t;}private void down(int i) {int left = 2 * i + 1;int right = 2 * i + 2;int max = i;if ( left < size && arr[max].priority() < arr[left].priority()) {max = left;}if (right < size && arr[max].priority() < arr[right].priority()) {max = right;}if (max != i) {swap(max,i);down(max);}}@Overridepublic E peek() {if (isEmpty()) {return null;}return (E)arr[0];}@Overridepublic boolean isEmpty() {return size == 0;}@Overridepublic boolean isFull() {return size == arr.length;} }
相关文章:
Java 数据结构篇-用数组、堆实现优先级队列
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 优先级队列说明 2.0 用数组实现优先级队列 3.0 无序数组实现优先级队列 3.1 无序数组实现优先级队列 - 入队列 offer(E value) 3.2 无序数组实现优先级队列 - 出…...

Reactor模型
目录 1.Reactor模型是什么2.Reactor 模型应用场景3.使用 Reactor 模型的软件4.Reactor 模型 与 Actor 模型 的关系 本文主要介绍Reactor模型基本概念以及应用场景。 1.Reactor模型是什么 Reactor模型是一种事件驱动的设计模式,用于处理服务请求,它是由…...
【SpringCloud】通过Redis手动更新Ribbon缓存来解决Eureka微服务架构中服务下线感知的问题
文章目录 前言1.第一次尝试1.1服务被调用方更新1.2压测第一次尝试1.3 问题分析1.4 同步的不是最新列表 2.第二次尝试2.1调用方过滤下线服务2.2压测第二次尝试2.3优化 写到最后 前言 在上文的基础上,通过压测的结果可以看出,使用DiscoveryManager下线服务…...
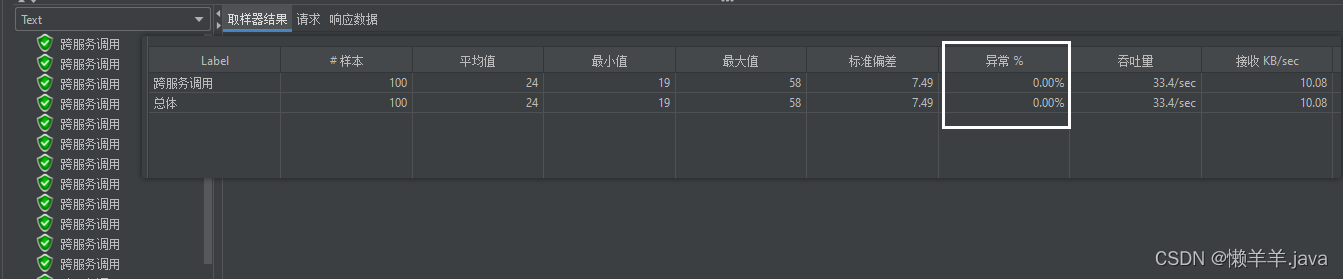
如何做好性能压测?压测环境设计和搭建的7个步骤你知道吗?
简介:一般来说,保证执行性能压测的环境和生产环境高度一致是执行一次有效性能压测的首要原则。有时候,即便是压测环境和生产环境有很细微的差别,都有可能导致整个压测活动评测出来的结果不准确。 1. 性能环境要考虑的要素 1.1 系…...
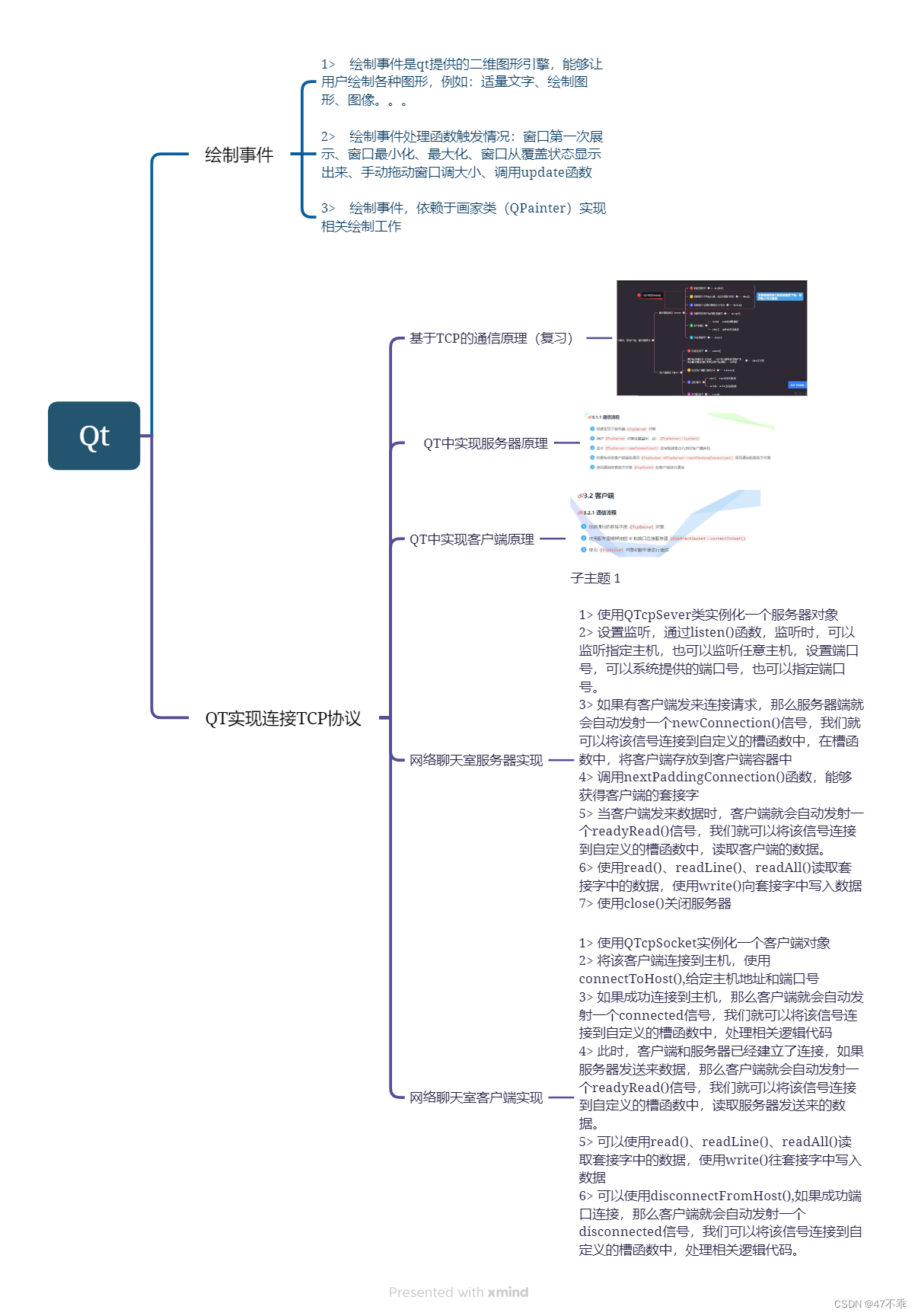
Qt12.13
...
(五))
目标检测YOLO系列从入门到精通技术详解100篇-【目标检测】SLAM(基础篇)(五)
目录 前言 几个相关概念 双目视惯雷达SLAM 相关工作 系统综述 视觉前端...
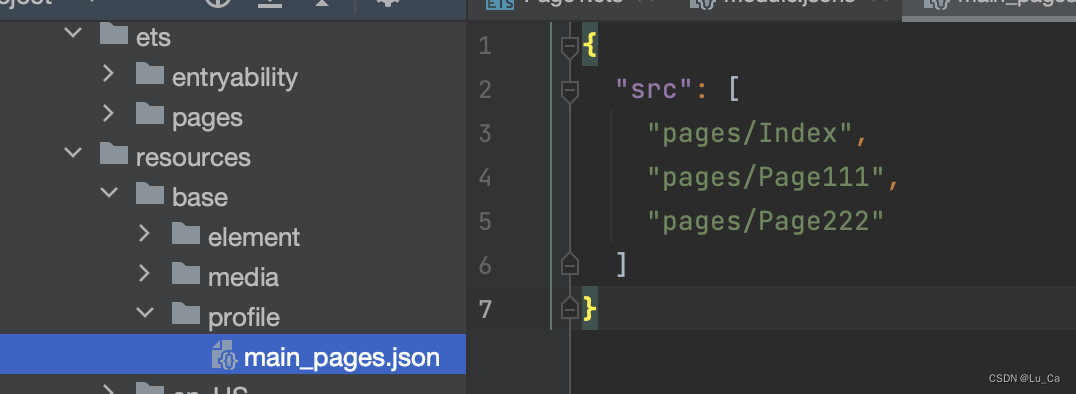
鸿蒙开发之页面与组件生命周期
一、页面间的跳转 创建文件的时候记得选择创建page文件,这样就可以在main->resources->profile->main_pages.json中自动形成页面对应的路由了。如果创建的时候你选择了ArkTS文件,那么需要手动修改main_pages.json文件中,添加相应的…...
的详解一)
Kotlin开发之低功耗蓝牙(引用三方库)的详解一
在我们工作中,如果涉及到软硬结合,经常会用到蓝牙,而蓝牙有两种:一种是普通的蓝牙,一种是低功耗的蓝牙,今天我们主要讲解的是低功耗蓝牙:主要根据第三方库进行的讲解 第一步:在使用…...

5G/4G工业DTU扬尘在线监测:解决工地扬尘困扰的最佳方案
在如今快速发展的工业环境中,扬尘污染成为了一个严重的问题。工地扬尘不仅对环境造成污染,还对工作人员的健康产生负面影响。为了解决这一问题,5G/4G工业DTU扬尘在线监测应运而生。 5G/4G工业DTU扬尘在线监测原理 5G/4G工业DTU扬尘在线监测是…...

思源黑体某些字显示成日式中文,太先进了(附解法)
由于字体版权问题,公司外发的材料一般都需要把字体换成“思源黑体”才可以。 很久以前下载过显示为“Noto Sans CJK”的思源黑,后来改成了“SourceHanSans”,一直以为自己的思源黑体是正常的。 然后问题来了:在替换ppt里的字体后…...
.NET医院检验系统LIS源码,使用了oracle数据库,保证数据的隔离和安全性
医院检验系统LIS源码,LIS系统全套商业源码 LIS系统实现了实验室人力资源管理、标本管理、日常事务管理、网络管理、检验数据管理(采集、传输、处理、输出、发布)、报表管理过程的自动化,使实验室的操作人员和管理者从繁杂的手工劳…...

html实现动漫视频网站模板源码
文章目录 1.视频设计来源1.1 主界面1.2 动漫、电视剧、电影视频界面1.3 播放视频界面1.4 娱乐前线新闻界面1.5 关于我们界面 2.效果和源码2.1 动态效果2.2 源代码 源码下载 作者:xcLeigh 文章地址:https://blog.csdn.net/weixin_43151418/article/detail…...
python zblog API实现类似XMLRPC/发布文章
我发现python对Zblog的XML发布并不友好,虽然也有对应的模块,但是远远没有XPCRPC更直接方便,但是使用xmlRpc是直接给发布文章带来了不小的便利,但是对系统也并不友好,但是zblog也开放了Api,但是干部子弟不乐…...
后台业务管理系统原型模板,Axure后台组件库(整套后台管理页面)
后台业务系统需要产品经理超强的逻辑思维能力和业务理解能力,整理了一批后台原型组件及完整的用 Axure 8 制作的后台系统页面,方便产品经理们快速上手制作后台原型。 包括交互元件、首页、商品、订单、库存、用户、促销、运营、内容、统计、财务、设置、…...

kyuubi整合flink yarn application model
目录 概述配置flink 配置kyuubi 配置kyuubi-defaults.confkyuubi-env.shhive 验证启动kyuubibeeline 连接使用hive catalogsql测试 结束 概述 flink 版本 1.17.1、kyuubi 1.8.0、hive 3.1.3、paimon 0.5 整合过程中,需要注意对应的版本。 注意以上版本 姊妹篇 k…...

使用openpyxl调整Excel的宽度
逐行加载Excel,并将行宽调整为行中的最大字符数。 希望在打开 Excel 时能够看到所有字符。 失败代码: #失败代码: wb openpyxl.load_workbook(./targetExcelFile.xlsx) ws wb.worksheets[0]for col in ws.iter_cols():max_length 0colum…...

前端面试——CSS面经(持续更新)
1. CSS选择器及其优先级 !important > 行内样式 > id选择器 > 类/伪类/属性选择器 > 标签/伪元素选择器 > 子/后台选择器 > *通配符 2. 重排和重绘是什么?浏览器的渲染机制是什么? 重排(回流):当增加或删除dom节点&…...
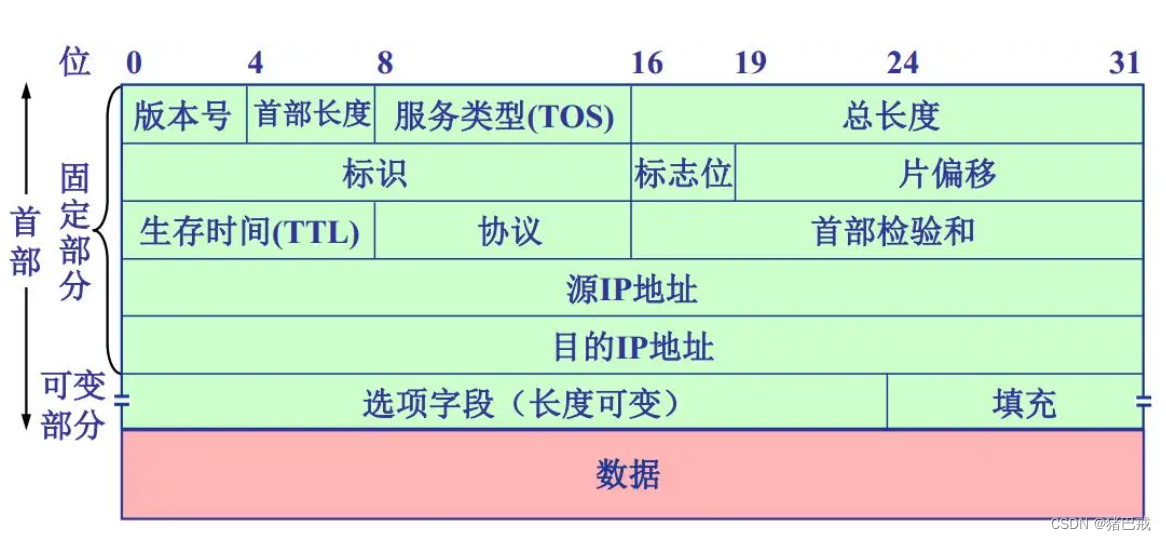
【C语言】结构体实现位段
引言 对位段进行介绍,什么是位段,位段如何节省空间,位段的内存分布,位段存在的跨平台问题,及位段的应用。 ✨ 猪巴戒:个人主页✨ 所属专栏:《C语言进阶》 🎈跟着猪巴戒,…...
学习资料)
IEEE RAS 机器人最优控制(Model-based Optimization for Robotics)学习资料
系列文章目录 前言 电气和电子工程师学会机器人模型优化技术委员会 一、学习资料 1.1 教程和暑期学校 2020 年 Memmo 欧盟项目暑期班2019年Memmo欧盟项目冬季学校Matthias Gerdts(德国慕尼黑联邦国防军大学)在拜罗伊特 OMPC 2013 上举办的最优控制教程…...
redis中缓存雪崩,缓存穿透,缓存击穿等
缓存雪崩 由于原有缓存失效(或者数据未加载到缓存中),新缓存未到期间(缓存正常从Redis中获取,如下图)所有原本应该访问缓存的请求都去查询数据库了,而对数据库CPU和内存造成巨大压力,…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
