排序-归并排序与计数排序
文章目录
- 一、归并排序
- 1、概念
- 2、过程
- 3、代码实现
- 4、复杂度
- 5、稳定性
- 二、 计数排序
- 1、思路
- 2、代码实现
- 3、复杂度:
- 4、稳定性
一、归并排序
1、概念
是建立在归并操作上的一种有效,稳定的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
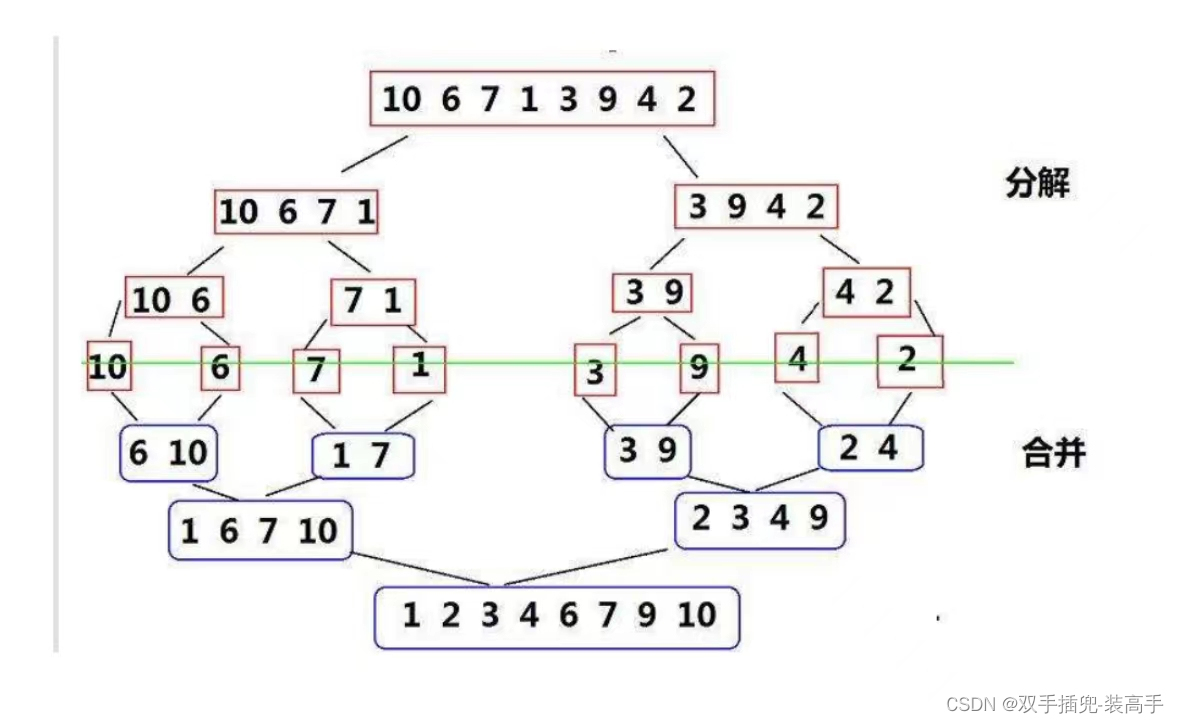
2、过程
假设前提:
左半区间 ->有序
右半区间 ->有序
怎么使左右排序呢?
当只剩下一个元素时我们可以默认其为有序的,所以我们可以利用递归将数组中的元素划分为一个,再两组两组合并,以此类推。
归并,依次对比取小的放到新到临时数组中,完成排序后再将临时数组的数据拷贝回原来的数组
过程图:
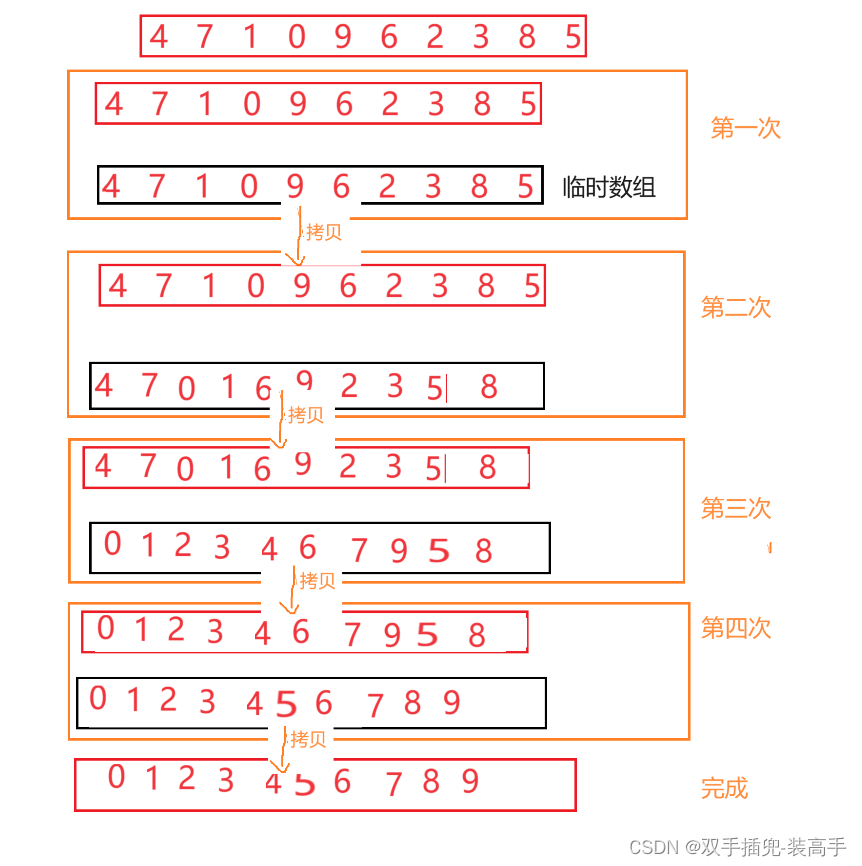
3、代码实现
递归:
void Print(int* arr, int n) {for (int i = 0; i < n; i++)printf("%d ", arr[i]);
}
//递归void _MergeSort(int *a,int *t,int left,int right) {//结束条件if (left >= right)return;int mid = (left + right) >> 1;//取中间数,划分区间//[left mid] [mid+1 right]//递归_MergeSort(a, t, left, mid);_MergeSort(a, t, mid + 1, right);//回归int begin1 = left, end1 = mid;//左区间int begin2 = mid + 1 , end2 = right;//右区间//临时数组下标->对应的是数组a的下标int index = left;//当左区间或者右区间,遍历完了就结束了while (begin1 <= end1 && begin2 <= end2) {//选择小的放进临时数组if (a[begin1] < a[begin2])t[index++] = a[begin1++];elset[index++] = a[begin2++];}//判断左右两边是否都空了,不为空将后面补上while (begin1 <= end1)t[index++] = a[begin1++];while (begin2 <= end2)t[index++] = a[begin2++];//最后拷贝回去for (int i = left; i <= right; ++i)a[i] = t[i];}
void MergeSort(int* a, int n) {int* t = (int*)malloc(sizeof(int) * n);_MergeSort(a, t, 0, n - 1);free(t);
}int main() {int a[] = { 3,7,1,0,9,6,2,3,8,5 };MergeSort(a, sizeof(a) / sizeof(a[0]));Print(a, sizeof(a) / sizeof(a[0]));return 0;
}
递归图(左边,先递后归):
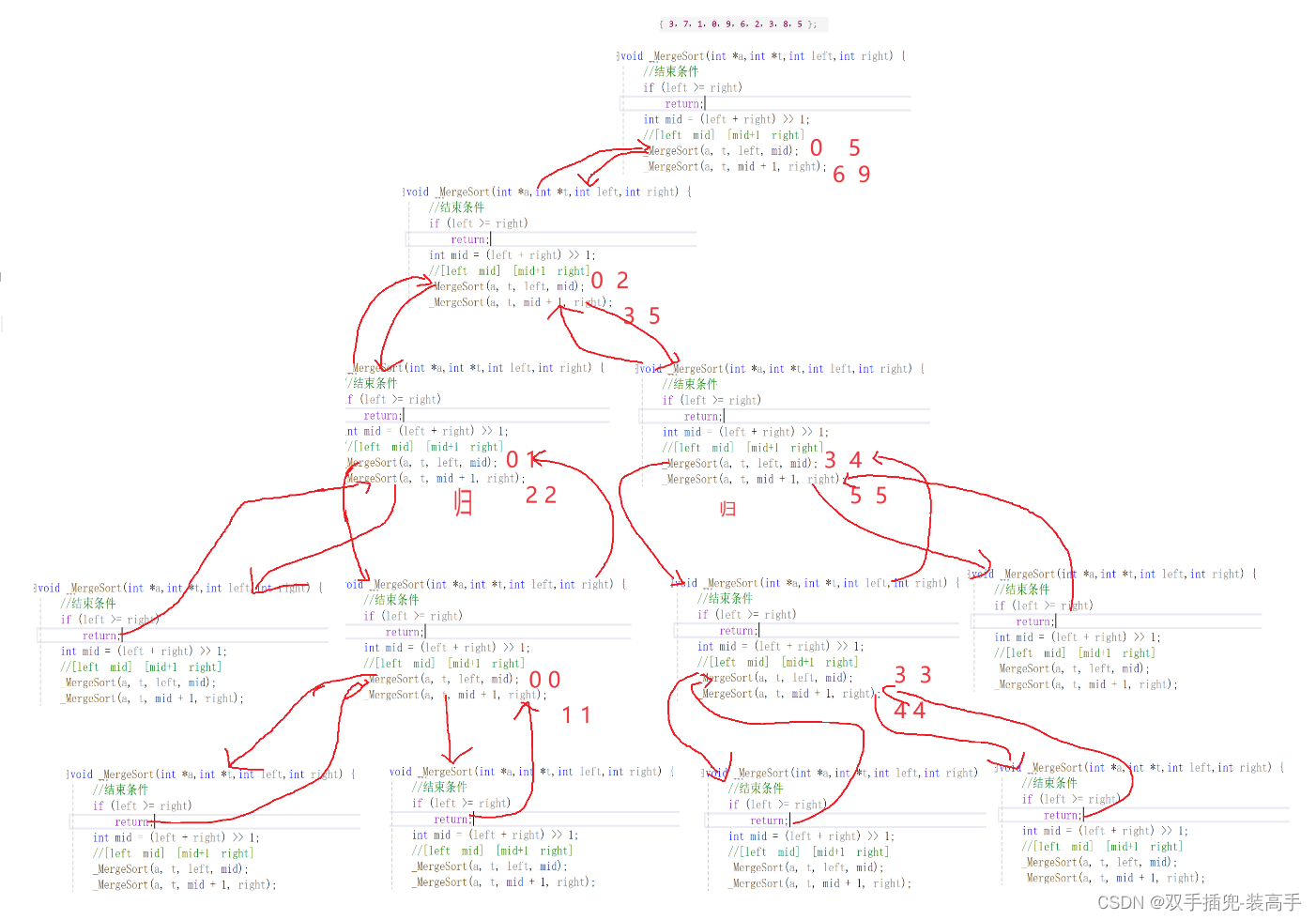
非递归:
我们通过循环来实现非递归
(1)设置一个gap来划分归并个数,先设置gap=1,这样控制第一次是两个数合并,gap再乘2,来递增,当 gap>n(数组大小)时结束
(2)在合并的过程中可能出现两种情况
a.合并过程中右边没元素
如:

解决办法:因为已经排好了,直接打破循环即可
b,右边有元素但是不够
如:
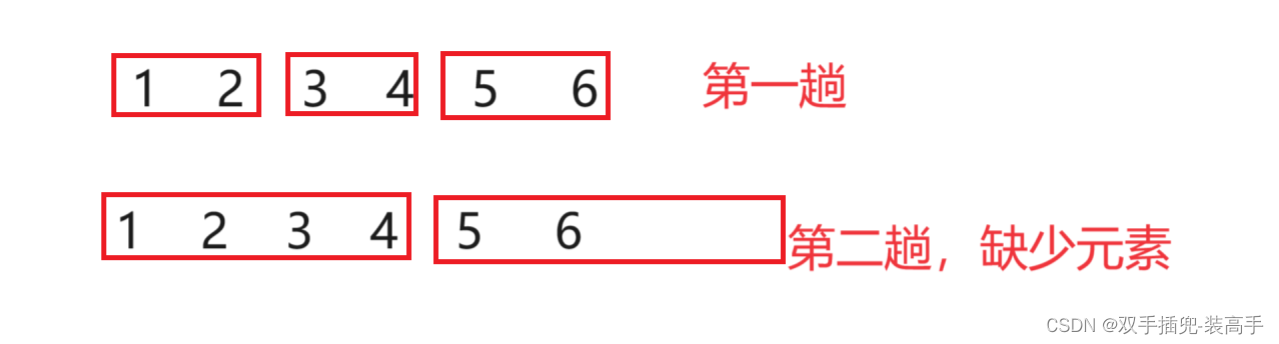
解决办法:进行纠正,将右端的下标改为 n-1(数组大小-1)
代码实现:
//非递归void MergeSortNonR(int* a, int* t,int n) {int gap= 1;//划分一次归并多少个元素//结束条件while (gap<n) {for (int i = 0; i < n; i += 2*gap) {//通过gap划分区间int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + gap * 2 - 1;//情况a,此时直接打破即可if (begin2 >= n)break;//情况b,进行纠正if (end2 >= n)end2 = n - 1;int index = i;//从控制的区间最小的位置开始//下面过程与递归过程一样while (begin1 <= end1 && begin2 <= end2) {if (a[begin1] < a[begin2])t[index++] = a[begin1++];elset[index++] = a[begin2++];}while (begin1 <= end1)t[index++] = a[begin1++];while (begin2 <= end2)t[index++] = a[begin2++];for (int j = i; j <= end2; j++)a[j] = t[j];}gap *= 2;//每次加倍}
}void MergeSort(int* a, int n) {int* t = (int*)malloc(sizeof(int) * n);MergeSortNonR(a, t, n);free(t);
}int main() {int a[] = { 6,3,7,1,9,5,2,8,0,4 };MergeSort(a, sizeof(a) / sizeof(a[0]));Print(a, sizeof(a) / sizeof(a[0]));return 0;
}
4、复杂度
时间复杂度:
(1)循环部分:N
(2)递归部分:因为每次都减半所以就是logN(以2为底)
所以时间复杂度为:O(N*logN)
空间复杂度:
因为要重新开辟一个数组,所以空间复杂度为O(N)
5、稳定性
在归并过程中相同的元素的顺序不会发生改变,所以是稳定的
二、 计数排序
1、思路
通过映射统计每个数出现的次数,再使用次数排序
如:

上述是以最大数去创建空间
但是如果遇到一个很大的数的话就需要我们创建空间时就会很浪费
如:
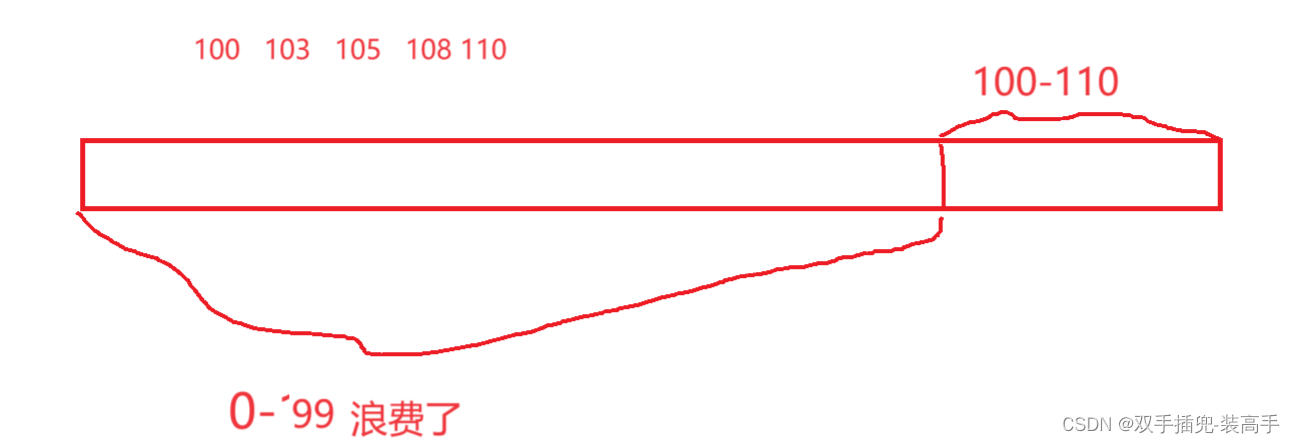
解决:找到范围,使用范围+1去创建临时空间
2、代码实现
//计数排序
void CountSort(int* a, int n) {int max = a[0];int min = a[0];//求出数组的范围for (int i = 0; i < n; i++) {if (max < a[i])max = a[i];if (min > a[i])min = a[i];}int t = max - min+1;//临时空间int* p = (int*)calloc(t,sizeof(int));//统计个数for (int j = 0; j < n; j++) {//a[j]-min当下标,我们下次直接加回min即可p[a[j] - min]++;}int i = 0;//按顺序拷贝回原来的数组for (int j = 0; j < t; j++) {while (p[j]) {a[i] = j + min;i++;p[j]--;}}free(p);p = NULL;
}
3、复杂度:
空间复杂度:因为要创建临时的空间,所以复杂度为O(N);
时间复杂度:O(N+t)
4、稳定性
在统计和重新排序过程中相同元素可能位置发生交换,所以为不稳定
以上就是我的分享了,如果有什么错误,欢迎在评论区留言。
最后,谢谢大家的观看!
相关文章:

排序-归并排序与计数排序
文章目录 一、归并排序1、概念2、过程3、代码实现4、复杂度5、稳定性 二、 计数排序1、思路2、代码实现3、复杂度:4、稳定性 一、归并排序 1、概念 是建立在归并操作上的一种有效,稳定的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已…...
国产数据库适配-人大金仓(kingbase V8R3)
金仓数据库是基于POSTGRE_SQL 参考资料 国产数据库人大金仓踩坑记录和函数适配_金仓数据库关系不存在-CSDN博客 Springboot工程 适配人大金仓 kingbase V8R3 引入驱动包和方言包 hibernate-5.2.17.Finaldialect.jar kingbase8-8.2.0.jar application.yml文件 driver-cla…...
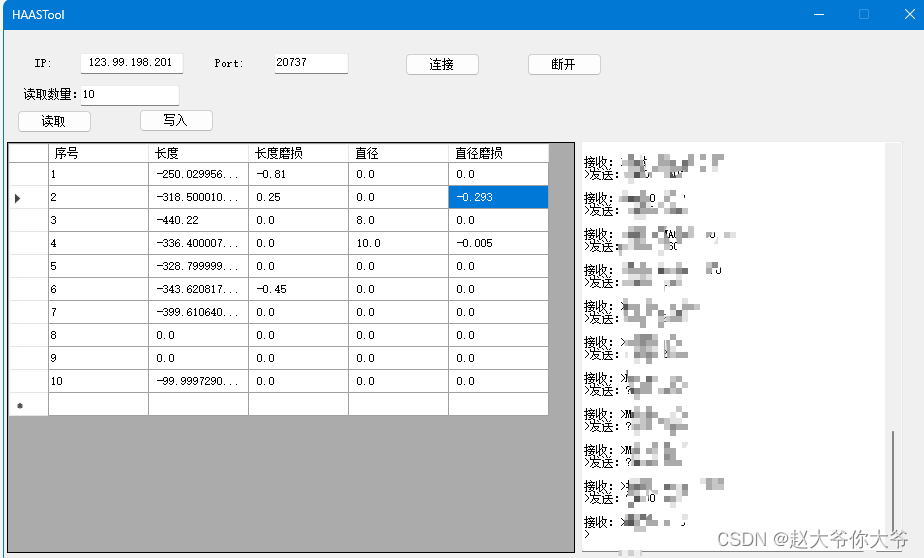
HAAS 哈斯机床 读写刀补数据
哈斯机床不管是串口机床还是网口机床 都提供了Q命令 可以使用Q命令 进行刀具补偿的读取和写入 最多支持200把刀的 读取和写入...
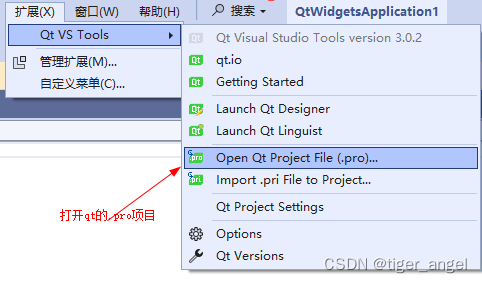
Visual studio+Qt开发环境搭建以及注意事项和打开qt的.pro项目
下载qt-然后安装5.14.2_msvc2017 不知道安装那个就全选5.14.2的父级按钮 https://download.qt.io/archive/qt/5.14/5.14.2/ 安装Visual studio,下载直接下一步就行 配置Visual studio的qt环境 在线安装-重启Visual studio会自动安装 离线安装-关闭Visual studio点击安装 关闭…...
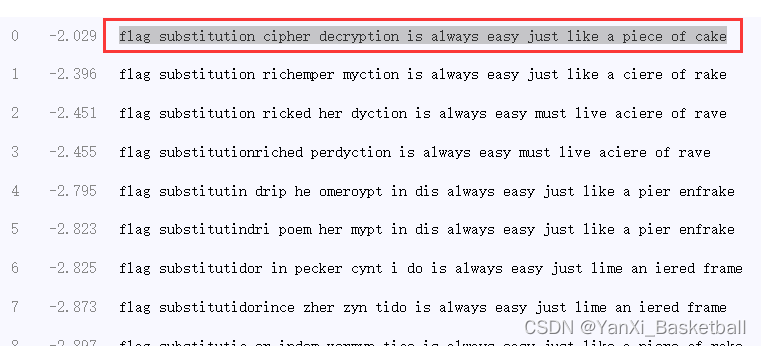
BUUCTF crypto做题记录(4)新手向
目录 一、大帝的密码武器 二、Windows系统密码 三、信息化时代的步伐 四、凯撒?替换?呵呵! 一、大帝的密码武器 下载的文件叫zip,应该是提示文件的后缀名是zip,把名字改成1.zip或者其他也行,主要保证后缀名是zip就…...
案例教程)
【ArcGIS微课1000例】0080:ArcGIS将shp转json(geojson)案例教程
本文以案例的形式,讲述在ArcGIS软件中,将矢量数据转为GeoJSON的方法。 扩展阅读:【GIS风暴】GeoJSON数据格式案例全解 文章目录 一、GeoJson简介二、ArcGIS将矢量数据转为GeoJSON一、GeoJson简介 GeoJSON是一种基于JSON的地理空间数据交换格式,它定义了几种类型JSON对象以…...

阿里云Centos8安装Dockers详细过程
一、卸载旧版本 较旧的 Docker 版本称为 docker 或 docker-engine 。如果已安装这些程序,请卸载它们以及相关的依赖项。 yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotate \do…...

leetcode 二数之和 三数之和 四数之和
leetcode 二数之和 三数之和 四数之和 又到了不想写博客的环节,不想归不想,有些事情还是要做的,今天总结的是多数之和的问题。 二数之和 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target …...

制衣厂生产ERP系统怎么样?制衣厂生产ERP软件哪个好
有很多的制衣厂在订单处理、物料、仓储、销售、仓储、物料编码、车间成本核算、计件工资核算等方面还存在不少改进空间。 而经过多年的发展,现如今制衣行业的竞争比较激烈,如何提升各业务部门协同效率,减少车间物料损耗,简化生产…...
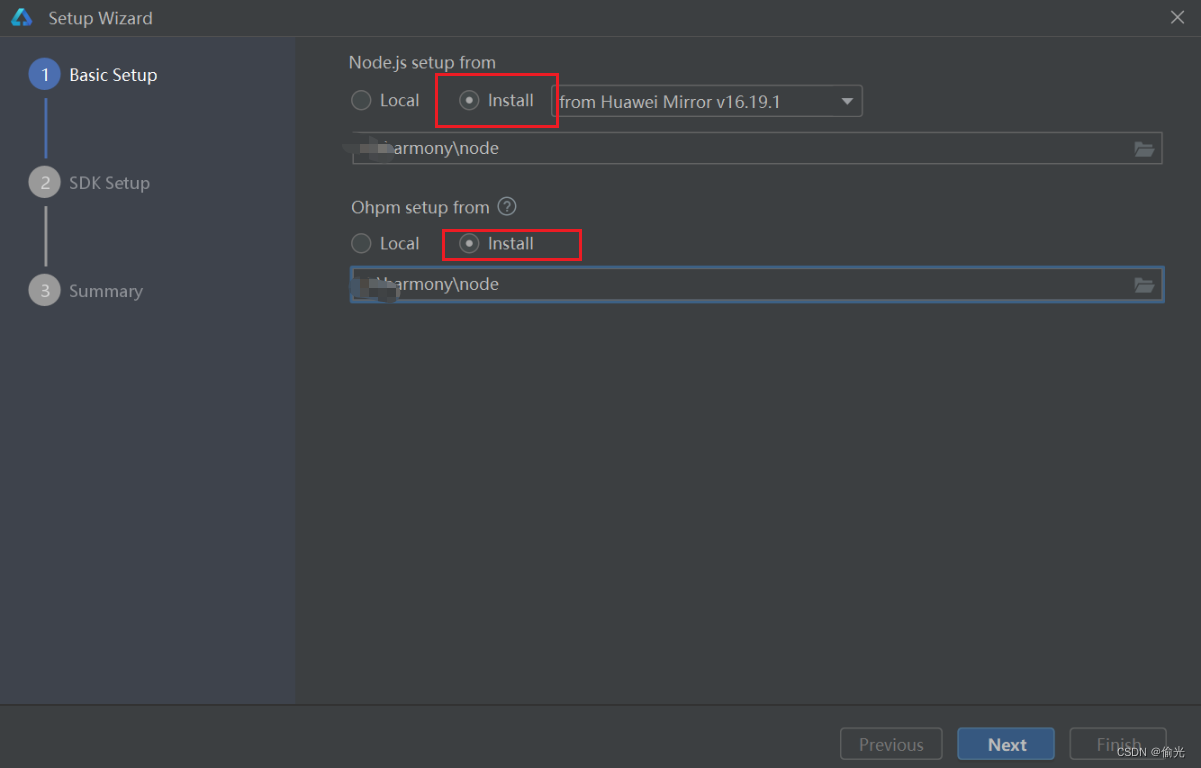
安装 DevEco Studio 后不能用本地 Node.js 打开
安装 DevEco Studio 后第一次打开时,不能用本地 Node.js 打开 答:因为本地 Node.js 文件夹名字中有空格 Node.js路径只能包含字母、数字、“。”、“_”、“-”、“:”和“V” 解决方法: 1.修改文件夹名称 2.重新下载 注意:找一…...
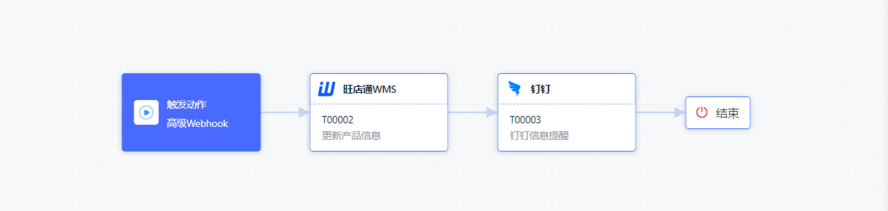
AppLink+WMS,实现仓储管理一体化
WMS像全能的库管员,可以在线还原真实仓库,让企业进行科学化、条理化、俯视化的仓库管理。 随着移动互联网和物流行业的快速发展,如何提高仓储管理的效率和准确性成为了企业关注的焦点。在这个背景下,结合AppLink和WMS系统&#x…...

如果是你,你选SOHO还是跟单?
昨天看到有人在讨论外贸跟单和外贸业务,谁的压力更大的问题?她们讨论的这个问题,源于一个年近四十准备二胎的宝妈,她做跟单十来年了,最近失业迷茫中,在纠结是否要SOHO?作为一个在工贸一体工厂做…...

大语言模型--能力
能力 大语言模型 能力从语言模型到任务模型的转化语言建模总结 从语言模型到任务模型的转化 在自然语言处理的世界中,语言模型 p p p是一种对代币序列 x 1 : L x_{1:L} x1:L这样的模型能够用于评估序列,例如 p ( t h e , m o u s e , a t e , t h e ,…...

安装LLaMA-Factory微调chatglm3,修改自我认知
安装git clone https://github.com/hiyouga/LLaMA-Factory.git conda create -n llama_factory python3.10 conda activate llama_factory cd LLaMA-Factory pip install -r requirements.txt 之后运行 单卡训练, CUDA_VISIBLE_DEVICES0 python src/train_web.py…...
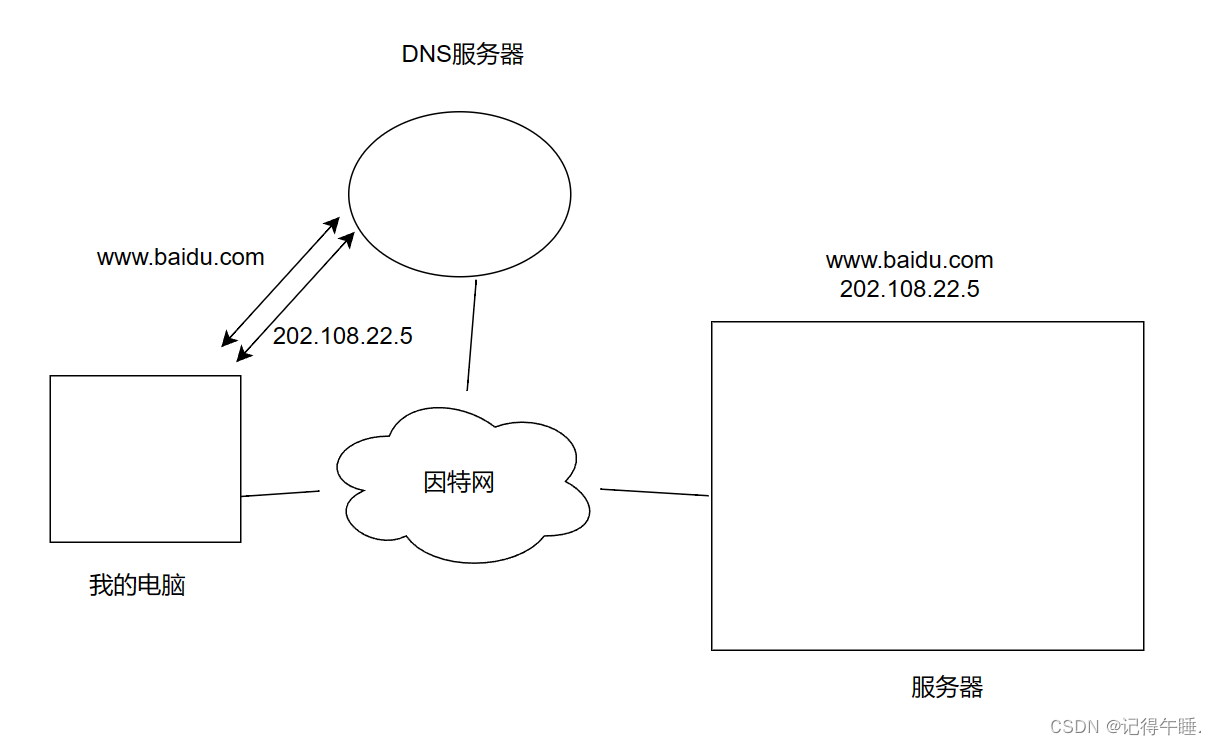
以太网协议与DNS
以太网协议 以太网协议DNS 以太网协议 以太网用于在计算机和其他网络设备之间传输数据,以太网既包含了数据链路层的内容,也包含了物理层的内容. 以太网数据报: 其中目的IP和源IP不是网络层的目的IP和源IP,而是mac地址.网络层的主要负责是整体的转发过程,数据链路层负责的是局…...

Spring Boot的日志
打印日志 打印日志的步骤: • 在程序中得到日志对象. • 使用日志对象输出要打印的内容 在程序中得到日志对象 在程序中获取日志对象需要使用日志工厂LoggerFactory,代码如下: package com.example.demo;import org.slf4j.Logger; import org.slf4j.LoggerFactory;public c…...
Cisco Packet Tracer配置命令——交换机篇
交换机VLAN配置 在简单的网络环境中,当交换机配置完端口后,即可直接应用,但若在复杂或规模较大的网络环境中,一般还要进行VLAN的规划,因此在交换机上还需进行 VLAN 的配置。交换机的VLAN配置工作主要有VLAN的建立与删…...

python单例模式
设计模式:单例模式(Singleton Pattern)。单例模式确保一个类只有一个实例,并提供一个全局访问点来获取这个实例。 class Singleton:_instance Nonedef __new__(cls):if cls._instance is None:cls._instance super().__new__(cl…...

环境保护:人类生存的最后机会
随着科技的进步和人类文明的不断发展,地球上的自然资源也在以惊人的速度消耗殆尽。人类对于环境的无止境的掠夺,使得我们的地球正面临着前所未有的环境危机。环境污染、全球变暖、大规模灭绝等问题不断困扰着我们,似乎指向了人类生存的最后机…...
头歌-Python 基础
第1关:建模与仿真 1、 建模过程,通常也称为数学优化建模(Mathematical Optimization Modeling),不同之处在于它可以确定特定场景的特定的、最优化或最佳的结果。这被称为诊断一个结果,因此命名为▁▁▁。 填空1答案:决…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...
