Leetcode69 x的平方根
x的平方根
- 题解1 袖珍计算器算法
- 题解2 二分查找
- 题解3 牛顿迭代
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4
输出:2
示例 2:
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842…, 由于返回类型是整数,小数部分将被舍去。
提示:
0 <= x <= 231 - 1
题解1 袖珍计算器算法

class Solution {
public:int mySqrt(int x) {if (x == 0) {return 0;}int ans = exp(0.5 * log(x));return ((long long)(ans + 1) * (ans + 1) <= x ? ans + 1 : ans);}
};
题解2 二分查找
class Solution {
public:int mySqrt(int x) {int l = 0, r = x, ans = -1;while (l <= r) {int mid = l + (r - l) / 2;if ((long long)mid * mid <= x) {ans = mid;l = mid + 1;} else {r = mid - 1;}}return ans;}
};
题解3 牛顿迭代
class Solution {
public:int mySqrt(int x) {if (x == 0) {return 0;}double C = x, x0 = x;while (true) {double xi = 0.5 * (x0 + C / x0);if (fabs(x0 - xi) < 1e-7) {break;}x0 = xi;}return int(x0);}
};
相关文章:

Leetcode69 x的平方根
x的平方根 题解1 袖珍计算器算法题解2 二分查找题解3 牛顿迭代 给你一个非负整数 x ,计算并返回 x 的 算术平方根 。 由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。 注意:不允许使用任何内置指数函数和算符&…...

在Linux上安装配置Nginx高性能Web服务器
1 前言 Nginx是一个高性能的开源Web服务器,同时也可以作为反向代理服务器、负载均衡器、HTTP缓存以及作为一个邮件代理服务器。它以其出色的性能和灵活性而闻名,被广泛用于处理高流量的网站和应用程序。本文将介绍在Linux环境中安装Nginx的步骤…...

LeetCode 每日一题 Day 11||贪心
2697. 字典序最小回文串 给你一个由 小写英文字母 组成的字符串 s ,你可以对其执行一些操作。在一步操作中,你可以用其他小写英文字母 替换 s 中的一个字符。 请你执行 尽可能少的操作 ,使 s 变成一个 回文串 。如果执行 最少 操作次数的方…...

ocr表格文字识别软件怎么使用?
现在的OCR软件几乎是傻瓜式的设计,操作很简单,像金鸣识别的软件无论是网页版还是电脑客户端又或是小程序,界面都简单明了,用户只需提交待识别的图片,然后点击提交识别,等识别完成就直接打开或下载打开就行了…...
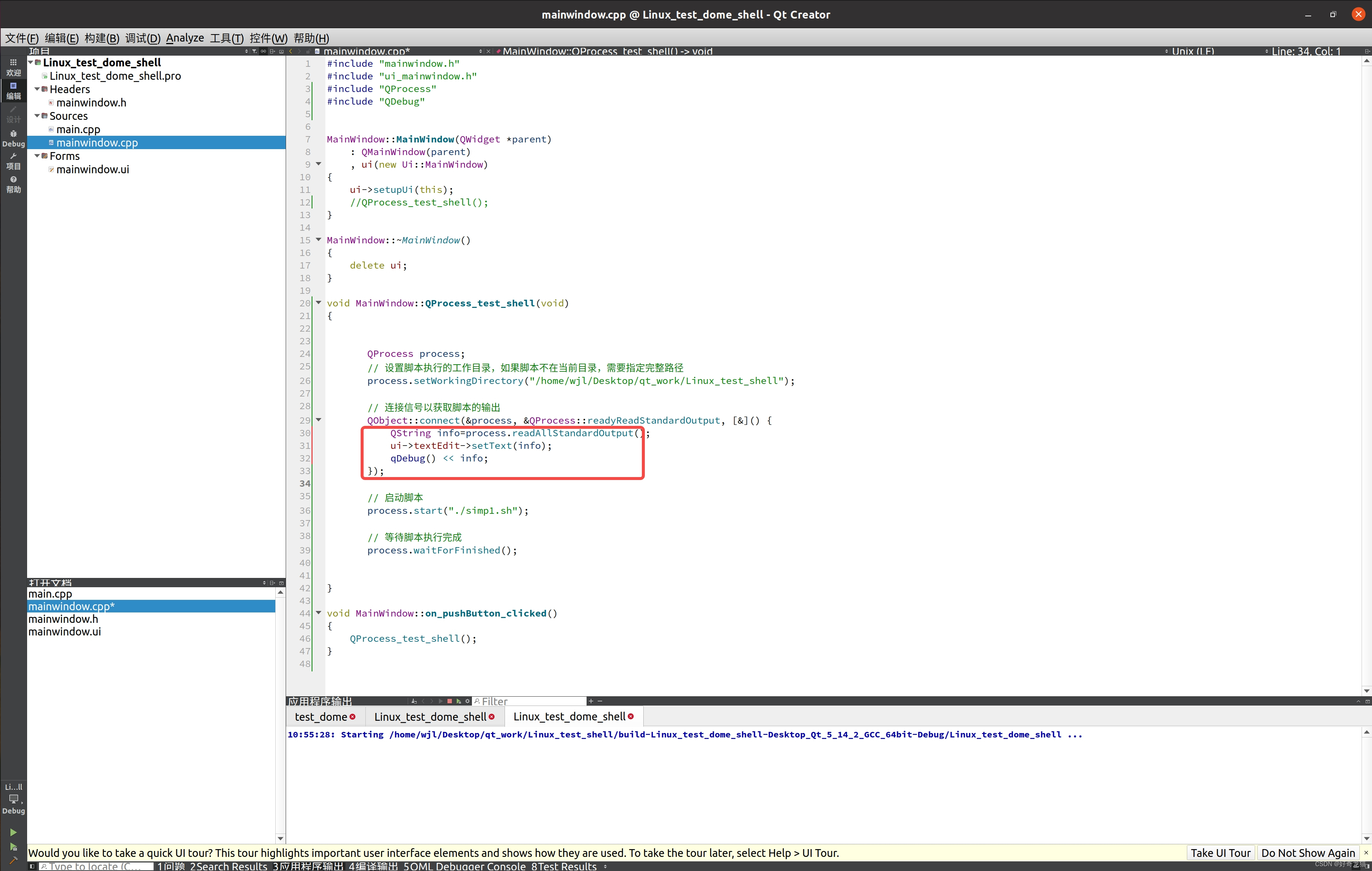
【QT 5 调试软件+Linux下调用脚本shell-经验总结+初步调试+基础样例】
【QT 5 调试软件Linux下调用脚本shell-经验总结初步调试基础样例】 1、前言2、实验环境3、自我总结4、实验过程(1)准备工作-脚本1)、准备工作-编写运行脚本文件2)、给权限3)、运行脚本 (2)进入q…...

使用 Goroutine 和 Channel 构建高并发程序
使用 Goroutine 和 Channel 构建高并发程序 文章目的与概要Golang 并发模型的重要性 Goroutine 和 Channel 的基础Goroutine:轻量级线程Channel:通信机制Goroutine 与 Channel 的协同工作 构建高并发模型的策略有效使用 Goroutine使用 Channel 进行数据传…...

大数据机器学习与深度学习——过拟合、欠拟合及机器学习算法分类
大数据机器学习与深度学习——过拟合、欠拟合及机器学习算法分类 过拟合,欠拟合 针对模型的拟合,这里引入两个概念:过拟合,欠拟合。 过拟合:在机器学习任务中,我们通常将数据集分为两部分:训…...

Lenovo联想拯救者Legion Y9000X 2021款(82BD)原装出厂Windows10系统
链接:https://pan.baidu.com/s/1GRTR7CAAQJdnh4tHbhQaDQ?pwdl42u 提取码:l42u 联想原厂WIN10系统自带所有驱动、出厂主题壁纸、系统属性专属LOGO标志、Office办公软件、联想电脑管家等预装程序 所需要工具:16G或以上的U盘 文件格式&am…...

pytorch中的transpose用法
注意:维数从0开始,0维 1维2维…,负数代表从右往左数,-1代表第一维,以此类推 import torch import numpy as np# 创建一个二维数组 arr torch.tensor([[[1, 2],[3, 4]],[[5, 6],[7, 8]]]) print("原始数组:"…...
SpringBoot面试题及答案(最新50道大厂版,持续更新)
在准备Spring Boot相关的面试题时,我发现网络上的资源往往缺乏深度和全面性。为了帮助广大Java程序员更好地准备面试,我花费了大量时间进行研究和整理,形成了这套Spring Boot面试题大全。 这套题库不仅包含了一系列经典的Spring Boot面试题及…...
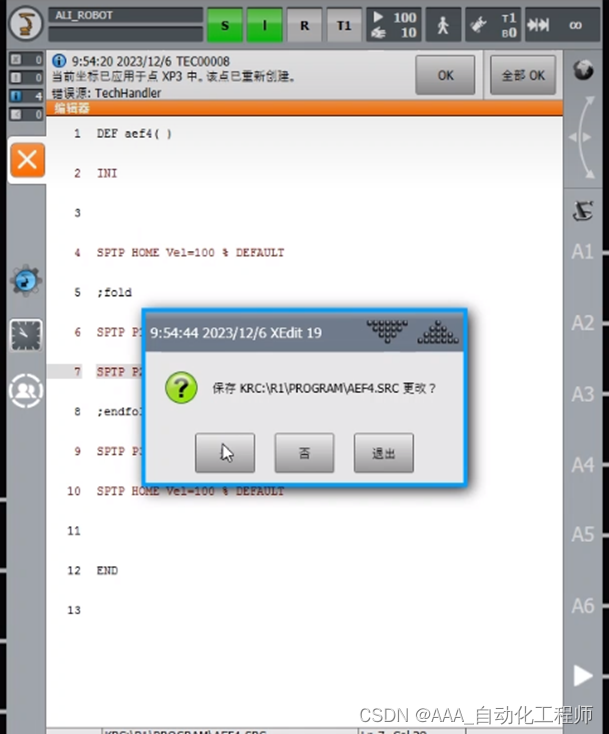
KUKA机器人如何隐藏程序或程序段?
KUKA机器人如何隐藏程序或程序段? 如下图所示,新建一个示例程序进行说明, 如下图所示,如果红框中的动作指令不想让别人看到,想隐藏起来,如何做到? 如下图所示,在想要隐藏的程序或程序段的前后,分别添加 ;fold 和 endfold指令(这里要注意是英文状态下的输入法), 如…...
--概述)
C++ STL(1)--概述
1. 简述 STL即标准模板库 Standard Template Library,包含了许多在计算机科学领域里所常用的基本数据结构和算法。STL具有高可重用性、高性能、高可移植性(跨平台)的优点。 两个特点: 1.1 数据结构和算法分离。 1.2 它不是面向对象的,是基于模…...
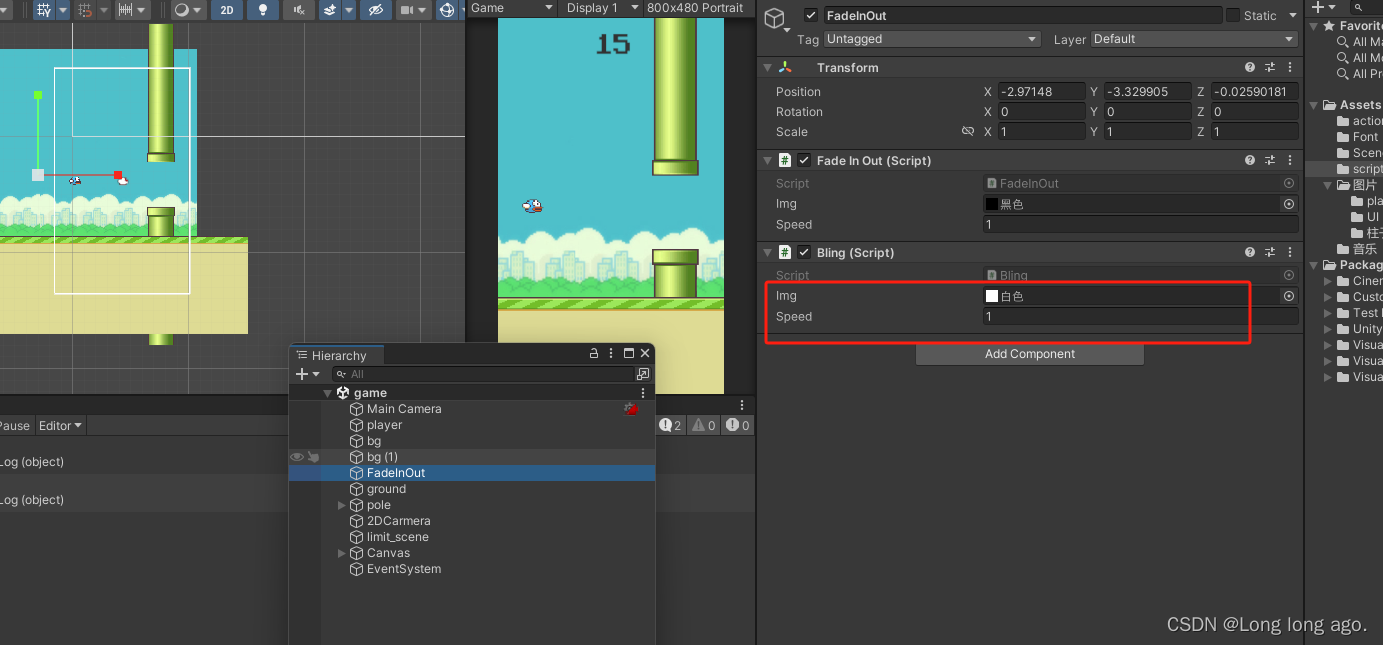
unity 2d 入门 飞翔小鸟 死亡闪烁特效(十三)
一、c#脚本 using System.Collections; using System.Collections.Generic; using UnityEngine;public class Bling : MonoBehaviour {public Texture img;public float speed;public static bool changeWhite false;private float alpha0f;// Start is called before the fi…...

Cannot find cache named ‘‘ for Builder Redis
当引入 Redissson 时,springCache 缓存机制失效 原因:springCache 默认使用本地缓存 Redisson 使用redis 缓存 最后都转成redis了。。。 总感觉哪不对 两者居然不共存...
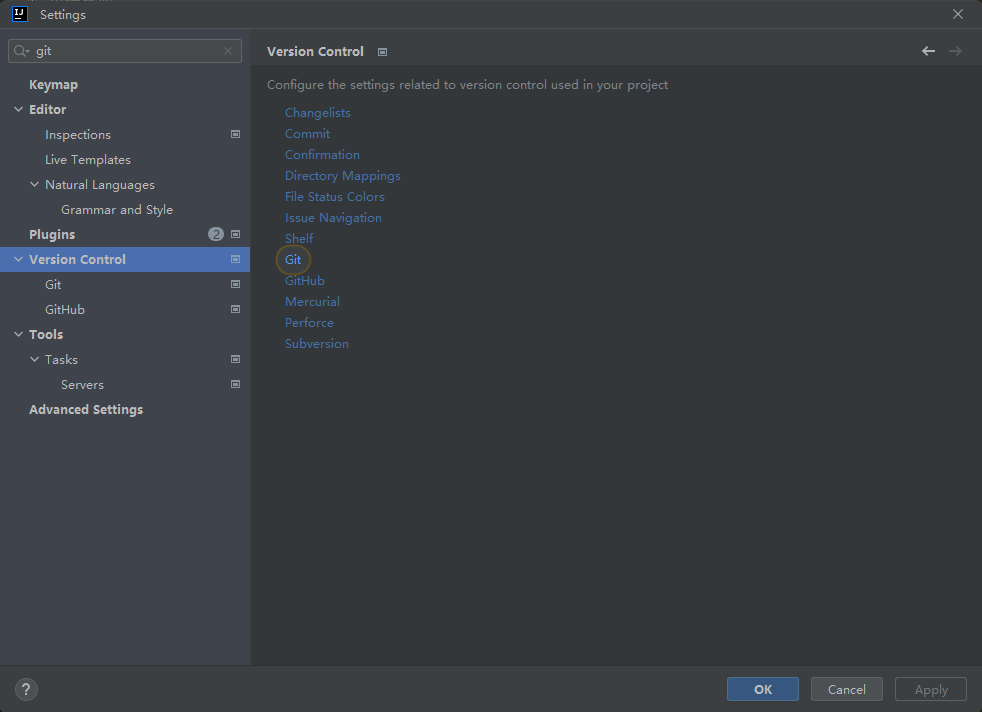
IntelliJ IDEA的下载安装配置步骤详解
引言 IntelliJ IDEA 是一款功能强大的集成开发环境,它具有许多优势,适用于各种开发过程。本文将介绍 IDEA 的主要优势,并提供详细的安装配置步骤。 介绍 IntelliJ IDEA(以下简称 IDEA)之所以被广泛使用,…...

光线追踪算法实现
我们已经涵盖了所有要说的内容! 我们现在准备编写第一个光线追踪器。 你现在应该能够猜测光线追踪算法是如何工作的。 首先,请花点时间注意一下,光在自然界中的传播只是从光源发出的无数光线,它们四处反弹,直到到达我…...

学习深度强化学习---第3部分----RL蒙特卡罗相关算法
文章目录 3.1节 蒙特卡罗法简介3.2节 蒙特卡罗策略评估3.3节 蒙特卡罗强化学习3.4节 异策略蒙特卡罗法 本部分视频所在地址:深度强化学习的理论与实践 3.1节 蒙特卡罗法简介 在其他学科中的蒙特卡罗法是一种抽样的方法。 如果状态转移概率是已知的,则是…...

linux虚拟机使用81-persistent-net.rule后接口名依然改变的问题处理
测试环境:vmware workstation17 、oracle linux 7.8 1. 复位原有ifname 1)nmcli c s 查看管理的网卡 [rootrac2 ~]# nmcli c s NAME UUID TYPE DEVICE enp0s3 5b01a9de-9552-45da-a84a-1ae6c9506354…...

ARMV8 - A64 - 跳转和返回指令
说明 C语言等高级语言,根据是否需要返回到触发跳转代码的下一条代码,跳转有两种语句: 不需要返回,例如:if,goto,switch,while等语句。需要返回,例如:函数调…...

QX320F28335,自研内核指令集,主频150MHz,自研工具链,纯国产DSP,硬件兼容TMS320F28335
32位单核CPU 主频150MHz flash 1M SRAM 500KB 单精度浮点运算FPU 3个4M精度12位的ADC 12个ePWM 6个HRPWM(150ps)...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
