Leetcode 2454. 下一个更大元素 IV
- Leetcode 2454. 下一个更大元素 IV
- 题目
- 给你一个下标从 0 开始的非负整数数组 nums 。对于 nums 中每一个整数,你必须找到对应元素的 第二大 整数。
- 如果 nums[j] 满足以下条件,那么我们称它为 nums[i] 的 第二大 整数:
- j >
- nums[j] > nums[i]
- 恰好存在 一个 k 满足 i < k < j 且 nums[k] > nums[i] 。
- 如果不存在 nums[j] ,那么第二大整数为 -1 。
- 比方说,数组 [1, 2, 4, 3] 中,1 的第二大整数是 4 ,2 的第二大整数是 3 ,3 和 4 的第二大整数是 -1 。
- 请你返回一个整数数组 answer ,其中 answer[i]是 nums[i] 的第二大整数。
- 1 <= nums.length <= 10 ^ 5
- 0 <= nums[i] <= 10 ^ 9
- 解法
- 反向思考 + 两次单调队列 + 排序二分/TreeSet:
- 第 1 步:
- 题目可以转化为两步处理,
- 通过下标 i 先找到 i 右边第一个 nums[k] > nums[i] 的 k,
- 再存储 i 和 k 在找到 k 右边第一个 nums[j] > nums[i] 的 nums[j]
- 第 2 步:
- 找 k 可以使用倒序遍历,
- 然后使用一个严格递减的单调栈,
- 每次第一个大于 nums[i] 的 nums 下标即为 k,
- 因为当求 i-1 时,要么 k 就是之前放入的 i(nums[i-1] < nums[i]),要么就是栈里剩下的某个元素(nums[i-1] >= nums[i])
- 将所有 i 与 k 均存起来,
- 第 3 步:
- 由于求 i-1 时,此时的 k1 可能比求 i 时的 k2 更靠右,此时 j1 就应该在 [0,k1) 对应的单调栈中,
- 在线求特别麻烦,因此可以考虑离线(即将所有 i-k 存起来,排序后统一处理)
- 第 4 步:
- 对 k 降序排,然后再次倒序使用一个严格递减的单调栈,
- 当遍历的值等于某个 k 时,使用 二分/TreeSet 栈中大于 nums[i] 的最小值,即为结果
- 遍历单调栈与 k 使用类似双指针的方式处理
- 第 5 步:
- 时间复杂度:O(n*logn)排序,空间复杂度:O(n)
- 代码
/*** 反向思考 + 两次单调队列 + 排序二分/TreeSet:** 第 1 步:* 题目可以转化为两步处理,* 通过下标 i 先找到 i 右边第一个 nums[k] > nums[i] 的 k,* 再存储 i 和 k 在找到 k 右边第一个 nums[j] > nums[i] 的 nums[j]** 第 2 步:* 找 k 可以使用倒序遍历,* 然后使用一个严格递减的单调栈,* 每次第一个大于 nums[i] 的 nums 下标即为 k,* * 因为当求 i-1 时,要么 k 就是之前放入的 i(nums[i-1] < nums[i]),要么就是栈里剩下的某个元素(nums[i-1] >= nums[i])* 将所有 i 与 k 均存起来,** 第 3 步:* 由于求 i-1 时,此时的 k1 可能比求 i 时的 k2 更靠右,此时 j1 就应该在 [0,k1) 对应的单调栈中,* 在线求特别麻烦,因此可以考虑离线(即将所有 i-k 存起来,排序后统一处理)** 第 4 步:* 对 k 降序排,然后再次倒序使用一个严格递减的单调栈,* 当遍历的值等于某个 k 时,使用 二分/TreeSet 栈中大于 nums[i] 的最小值,即为结果* 遍历单调栈与 k 使用类似双指针的方式处理** 第 5 步:* 时间复杂度:O(n*logn)排序,空间复杂度:O(n)**/public int[] secondGreaterElement(int[] nums) {int n = nums.length;// 所有 i 与 k 均存起来,k 不存在则使用 -1List<Pair<Integer, Integer>> indexList = new ArrayList<>();int[] res = new int[n];// 找 k 可以使用倒序遍历,然后使用一个严格递减的单调栈,Deque<Integer> decreaseStack = new LinkedList<>();for (int i = n - 1; i >= 0; i--) {while (!decreaseStack.isEmpty() && nums[decreaseStack.peekFirst()] <= nums[i]) {decreaseStack.pop();}indexList.add(new Pair<>(i, decreaseStack.isEmpty() ? -1 : decreaseStack.peekFirst()));// k 等于 -1 则结果也为 -1res[i] = -1;decreaseStack.push(i);}// 对 k 降序排,然后再次倒序使用一个严格递减的单调栈Collections.sort(indexList, (o1, o2) -> o2.getValue() - o1.getValue());
// System.out.println(indexList);// 当遍历的值等于某个 k 时,使用 二分/TreeSet 栈中大于 nums[i] 的最小值,即为结果TreeSet<Integer> treeSet = new TreeSet<>();decreaseStack.clear();int listIndex = 0;for (int i = n - 1; i >= 0 && listIndex < n; i--) {while (listIndex < n && i == indexList.get(listIndex).getValue()) {int numsIndex = indexList.get(listIndex).getKey();Integer resTemp = treeSet.higher(nums[numsIndex]);res[numsIndex] = resTemp == null ? -1 : resTemp;listIndex++;}while (!decreaseStack.isEmpty() && nums[decreaseStack.peekFirst()] <= nums[i]) {treeSet.remove(nums[decreaseStack.peekFirst()]);decreaseStack.pop();}treeSet.add(nums[i]);decreaseStack.push(i);}return res;}
相关文章:

Leetcode 2454. 下一个更大元素 IV
Leetcode 2454. 下一个更大元素 IV题目 给你一个下标从 0 开始的非负整数数组 nums 。对于 nums 中每一个整数,你必须找到对应元素的 第二大 整数。如果 nums[j] 满足以下条件,那么我们称它为 nums[i] 的 第二大 整数: j >nums[j] > nu…...

浏览器全屏按键同f11效果
模拟键f11 // for IE,这里和fullScreen相同,模拟按下F11键退出全屏 let wscript new ActiveXObject(WScript.Shell) if (wscript ! null) {wscript.SendKeys({F11}) }同f11键效果生效全屏函数 //判断是否是全屏状态 var isFull Math.abs(window.scree…...
CentOS 7.9 安装 k8s(详细教程)
🍿安装步骤 🍚安装前准备事项🍚安装docker🍚删除docker🍚安装yum工具🍚设置docker镜像源🍚安装指定版本docker🍚设置开启自启🍚阿里云镜像加速 🍚准备环境&am…...
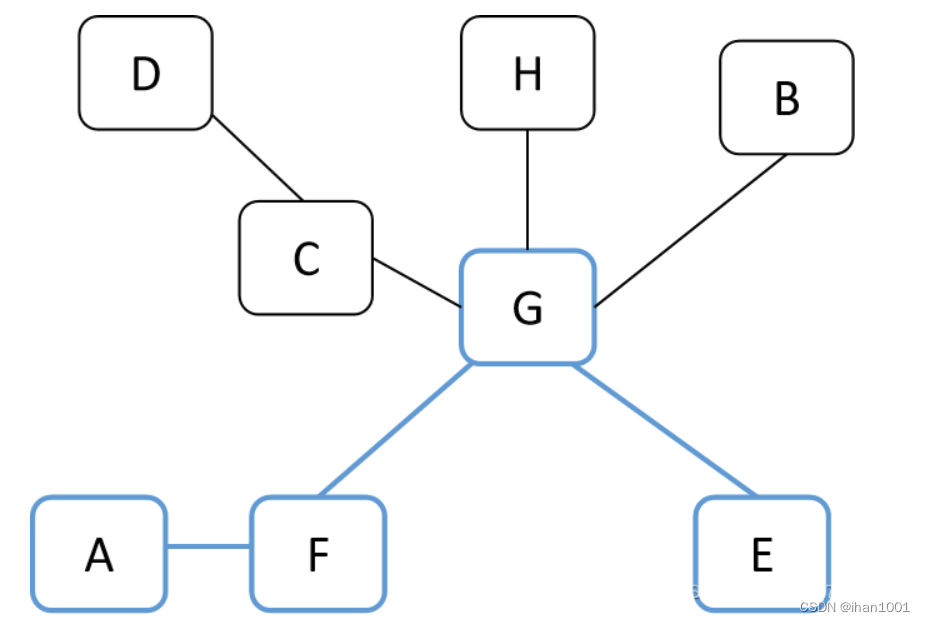
区块链的可拓展性研究【05】闪电网络
1.闪电网络:闪电网络是一种基于比特币区块链的 Layer2 扩容方案,它通过建立一个双向支付通道网络,实现了快速、低成本的小额支付。闪电网络的交易速度非常快,可以达到每秒数万笔交易,而且交易费用非常低,几…...
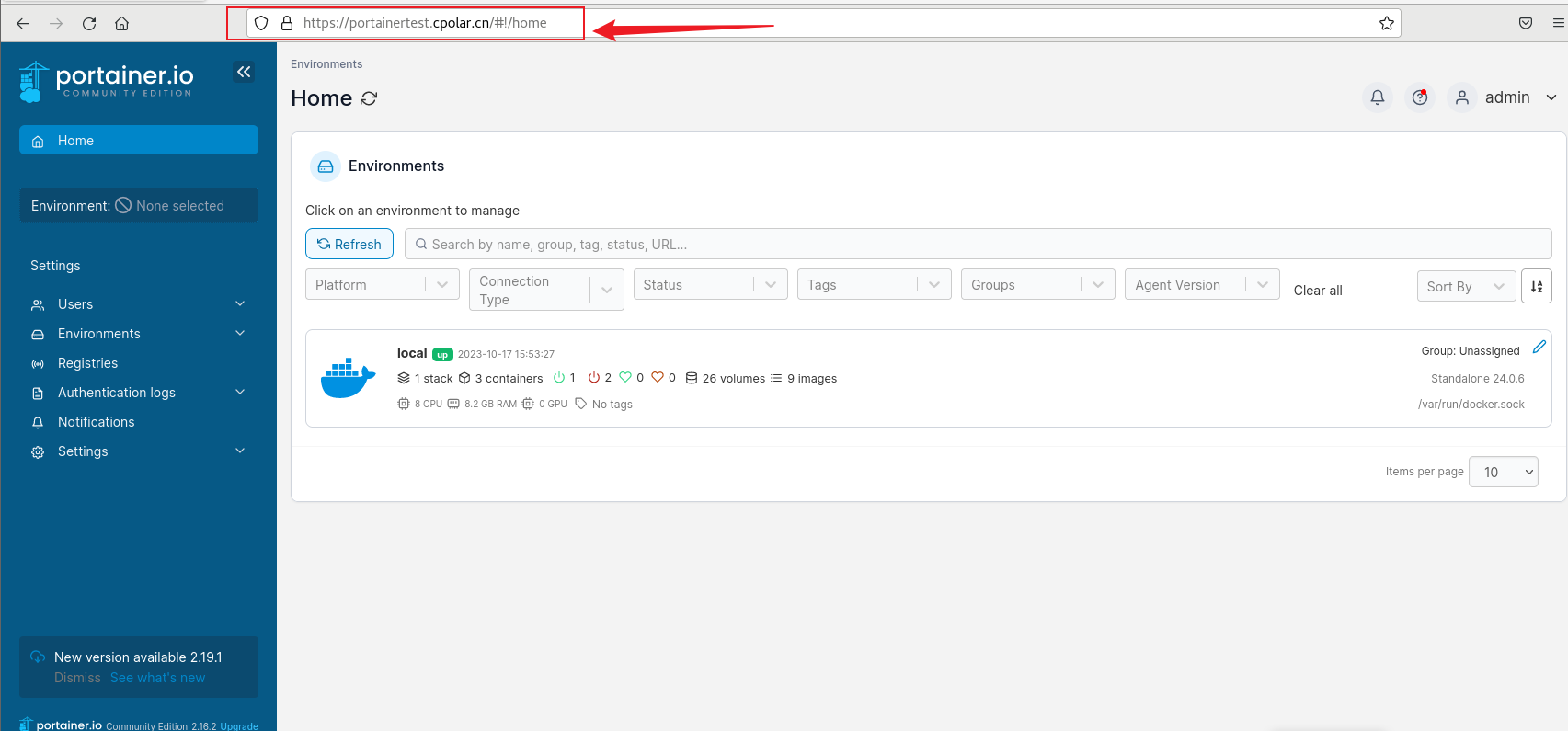
如何部署Portainer容器管理工具+cpolar内网穿透实现公网访问管理界面
文章目录 前言1. 部署Portainer2. 本地访问Portainer3. Linux 安装cpolar4. 配置Portainer 公网访问地址5. 公网远程访问Portainer6. 固定Portainer公网地址 前言 本文主要介绍如何本地安装Portainer并结合内网穿透工具实现任意浏览器远程访问管理界面。Portainer 是一个轻量级…...
Linux——Samba文件共享服务配置
SMB/CIFS协议 SMB协议(Server Message Block 又称Common Internet File System(CIFS)) 是由微软开发的网络传输协议,用来实现网络共享文件系统、打印机等资源。 SMB协议有多个版本和不同的兼容性。 SMBv1/CIFS: 也称为SMB1或CIFS。最初由Micr…...

自动驾驶右向辅助功能规范
目 录 Contents 目录 1. 介绍 Introduction. 8 1.1 此文档的范围和目的 Scope and Purpose of This Document 8 1.2 参考文档References. 9 1.3 文档的维护 Maintenance of the Document 10 1.4 缩略词Abbreviations. 10 1.5 文档概述Document Overview.. 11 1.6 功能…...

ASF-YOLO开源 | SSFF融合+TPE编码+CPAM注意力,精度提升!
目录 摘要 1 Introduction 2 Related work 2.1 Cell instance segmentation 2.2 Improved YOLO for instance segmentation 3 The proposed ASF-YOLO model 3.1 Overall architecture 3.2 Scale sequence feature fusion module 3.3 Triple feature encoding module …...

Mac 如何删除文件及文件夹?可以尝试使用终端进行删除
MacOS 是 Mac 电脑采用的操作系统,你知道 Mac 如何删除文件吗?除了直接将文件或者文件夹拖入废纸篓之外,我们还可以采用终端命令的办法去删除文件,本文为大家总结了 Mac 删除文件方法。 为何使用命令行删除文件 在使用 Mac 电脑…...
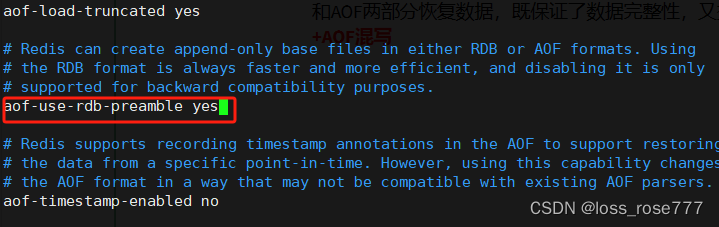
最新Redis7持久化(权威出版)
首先我们要知道什么是持久化:持久化是指将数据保存到磁盘上,以确保在Redis服务器重启时数据不会丢失。 Redis支持两种主要的持久化方式:RDB持久化和AOF持久化 下面让我依次给你介绍一下: RDB持久化 作用 这是将Redis数据保存…...

Redis权限管理体系(一):客户端名及用户名
在Redis6之前的版本中,因安全认证的主要方式是使用Redis实例的密码进行基础控制,而无法按照不同的应用来源配置不同账号以及更细粒度的操作权限控制来管理。本文先从client list中的信息入手,逐步了解Redis的客户端名设置、用户设置及权限控制…...

【数据库设计和SQL基础语法】--查询数据--排序
一、排序数据 1.1 ORDER BY子句 单列排序 单列排序是通过使用 ORDER BY 子句对查询结果按照单个列进行排序。以下是单列排序的一些示例: 升序排序(默认): SELECT column1, column2, ... FROM your_table_name ORDER BY column_t…...
【sqli靶场】第六关和第七关通关思路
目录 前言 一、sqli靶场第六关 1.1 判断注入类型 1.2 观察报错 1.3 使用extractvalue函数报错 1.4 爆出数据库中的表名 二、sqli靶场第七关 1.1 判断注入类型 1.2 判断数据表中的字段数 1.3 提示 1.4 构造poc爆库名 1.5 构造poc爆表名 1.6 构造poc爆字段名 1.7 构造poc获取账…...
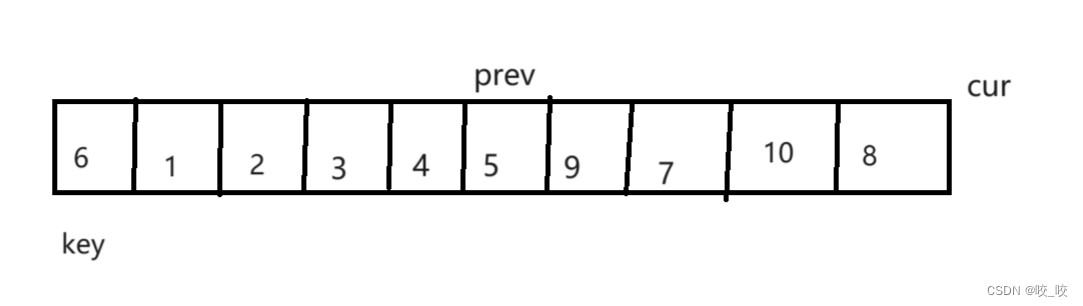
c语言快速排序(霍尔法、挖坑法、双指针法)图文详解
快速排序介绍: 快速排序是一种非常常用的排序方法,它在1962由C. A. R. Hoare(霍尔)提的一种二叉树结构的交换排序方法,故因此它又被称为霍尔划分,它基于分治的思想,所以整体思路是递归进行的。 …...

【mysql】锁的类型有哪些呢?
0 回答 根据数据的访问级别来区分: mysql锁分为共享锁和排他锁,也叫做读锁和写锁。读锁是共享的,可以通过lock in share mode实现,这时候只能读不能写。写锁是排他的,它会阻塞其他的写锁和读锁。 从颗粒度来区分&am…...

uniapp 显示文件流图片
如果是需要将文件流保存到相册,可以先转base64.详情见>uniapp app将base64保存到相册,uniapp app将文件流保存到相册-CSDN博客 uni.request({url: "www.baidu.com",data: {},header: {content-type:application/json,Authorization: "token"…...
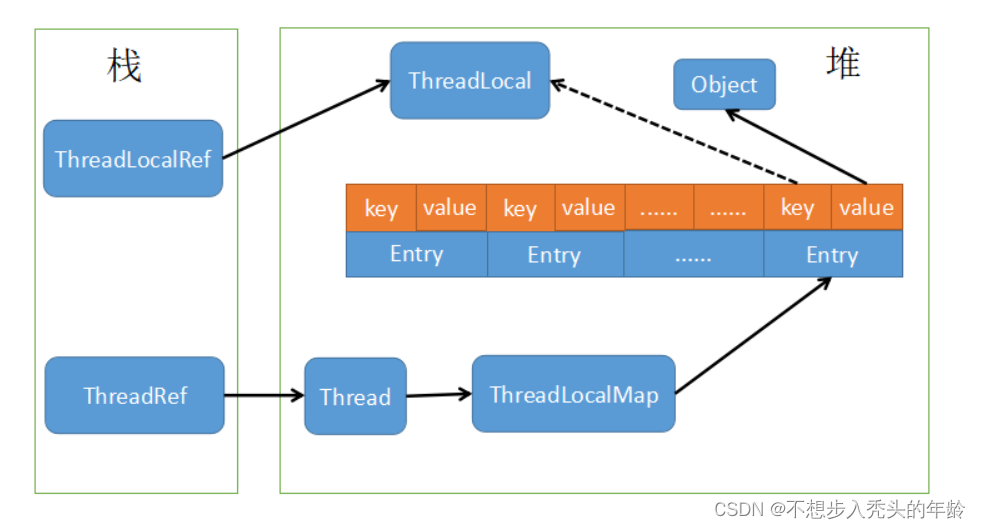
多线程------ThreadLocal详解
目录 1. 什么是 ThreadLocal? 2. 如何使用 ThreadLocal? 3. ThreadLocal 的作用 4. ThreadLocal 的应用场景 5. ThreadLocal 的注意事项 我的其他博客 ThreadLocal 是 Java 中一个很有用的类,它提供了线程局部变量的支持。线程局部变量…...
:随机数、密码、时间戳、日期和时间(格式化与解析)、时区、本地时间)
【C++】POCO学习总结(十六):随机数、密码、时间戳、日期和时间(格式化与解析)、时区、本地时间
【C】郭老二博文之:C目录 1、Poco::Random 随机数 1.1 说明 POCO包括一个伪随机数生成器(PRNG),使用非线性加性反馈算法,具有256位状态信息和长达269的周期。 PRNG可以生成31位的伪随机数。 它可以生成UInt32, char, bool, float和double…...

打补丁,生成.diff文件
作者:爱塔居 文章目录 目录 前言 步骤 一、在根目录上,输入添加指令 二、输入修改内容指令 三、生成补丁 前言 自己的理解,仅供参考,欢迎指正。 补丁的话,在我看来就是方便评审,更方便看修改代码吧。 步骤…...

《LeetCode力扣练习》代码随想录——字符串(KMP算法学习补充——针对next数组构建的回退步骤进行解释)
《LeetCode力扣练习》代码随想录——字符串(KMP算法学习补充——针对next数组构建的回退步骤进行解释) 学习路径 代码随想录:28. 实现 strStr() CSDN:【详解】KMP算法——多图,多例子(c语言) …...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...
