Vue的动画方式有几种
Vue的动画方式有几种?
Vue的动画方式主要分成两大类,一类是CSS动画,一类是JS动画
CSS动画中包含transition以及animation,但在Vue中只需要通过transition封装组件实现。
- CSS动画的类名主要包括:v-enter、v-enter-active、v-enter-to、v-leave、v-leave-active、v-leave-to- transition只允许有一个元素内容,appear、type、duration、mode等属性可以进行动画操作的设置
- mode属性设置以后需要给动画元素设置唯一key值
in-out: 新元素先进行过渡,完成之后当前元素过渡离开。
out-in: 当前元素先进行过渡,完成之后新元素过渡进入。- 一般情况下可以利用animate.css动画库内容进行CSS动画功能的实现
JS动画仍旧操作的是transition组件
- 设置的是属性钩子,内容包括before-enter、enter、after-enter、enter-cancelled、before-leave、leave、after-leave、leave-cancelled等
- 在 enter 和 leave 中必须使用 done 进行回调。否则,它们将被同步调用,过渡会立即完成
- 可以设置css属性为false,以免受css影响
- js动画同样可以利用js动画类库实现动画操作,比如Velocity.js
- 列表动画可以利用transition-group进行实现
到这里也就结束了,希望对您有所帮助。
相关文章:

Vue的动画方式有几种
Vue的动画方式有几种? Vue的动画方式主要分成两大类,一类是CSS动画,一类是JS动画 CSS动画中包含transition以及animation,但在Vue中只需要通过transition封装组件实现。 CSS动画的类名主要包括:v-enter、v-enter-acti…...

PyTorch: 基于【VGG16】处理MNIST数据集的图像分类任务【准确率98.9%+】
目录 引言在Conda虚拟环境下安装pytorch步骤一:利用代码自动下载mnist数据集步骤二:搭建基于VGG16的图像分类模型步骤三:训练模型步骤四:测试模型运行结果后续模型的优化和改进建议完整代码结束语 引言 在本博客中,小…...
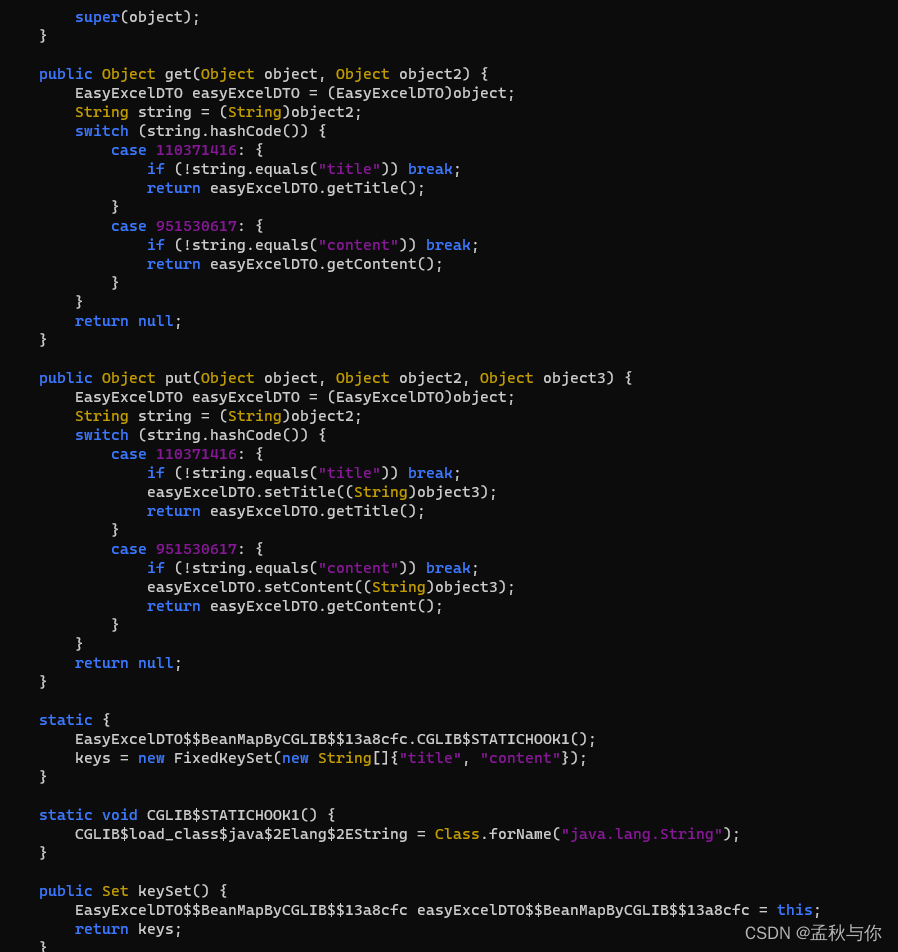
【lombok】从easyExcel read不到值到cglib @Accessors(chain = true)隐藏的大坑
背景: 在一次使用easyExcel.read 读取excel时,发现实体类字段没有值,在反复测试后,发现去掉Accessors(chain true)就正常了,为了验证原因,进行了一次代码跟踪 由于调用链路特别长,只列举出部分代码&#x…...

1-SaaS通识
云计算 讲SaaS必须先讲云计算。云计算通过互联网提供计算服务,包括服务器、存储、数据库、网络、应用等,采用按需付费的定价模式。 云计算的4种部署模式 公有云:由云服务商拥有和管理,就好比水电,居民共享ÿ…...

Spring Boot实现接口幂等
Spring Boot实现接口幂等 1、pom依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http:…...
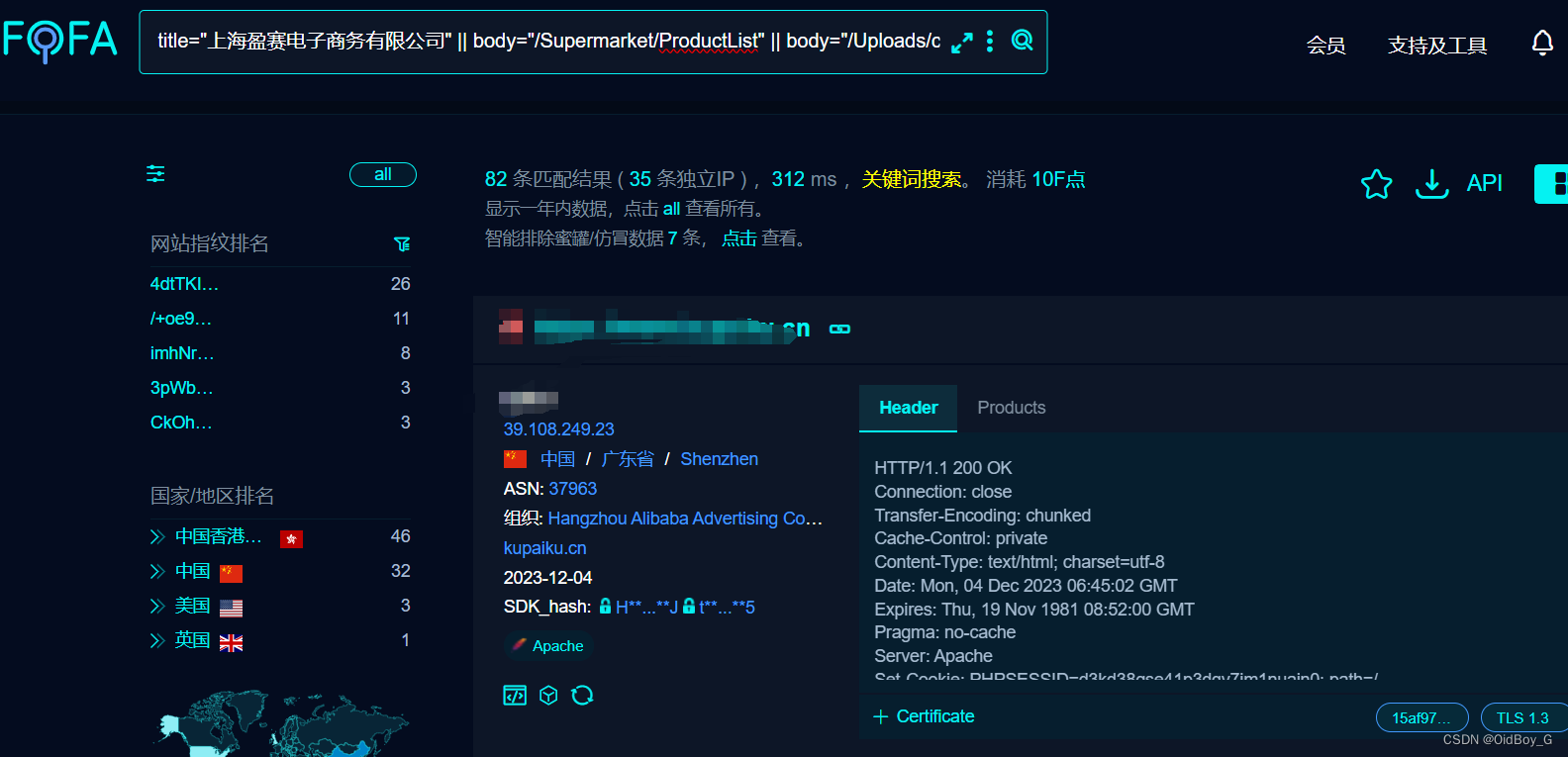
ShopsN commentUpload 文件上传漏洞复现
0x01 产品简介 ShopsN 是一款符合企业级商用标准全功能的真正允许免费商业用途的开源网店全网系统。 0x02 漏洞概述 ShopsN commentUpload 接口处存在任意文件上传漏洞,攻击者可以利用文件上传漏洞执行恶意代码、写入后门、读取敏感文件,从而可能导致服务器受到攻击并被控…...

【Qt5】ui文件最后会变成头文件
2023年12月14日,周四下午 我也是今天下午偶然间发现这个的 在使用Qt的uic(User Interface Compiler)工具编译ui文件时,会生成对应的头文件。 在Qt中,ui文件是用于描述用户界面的XML文件,而头文件是用于在…...
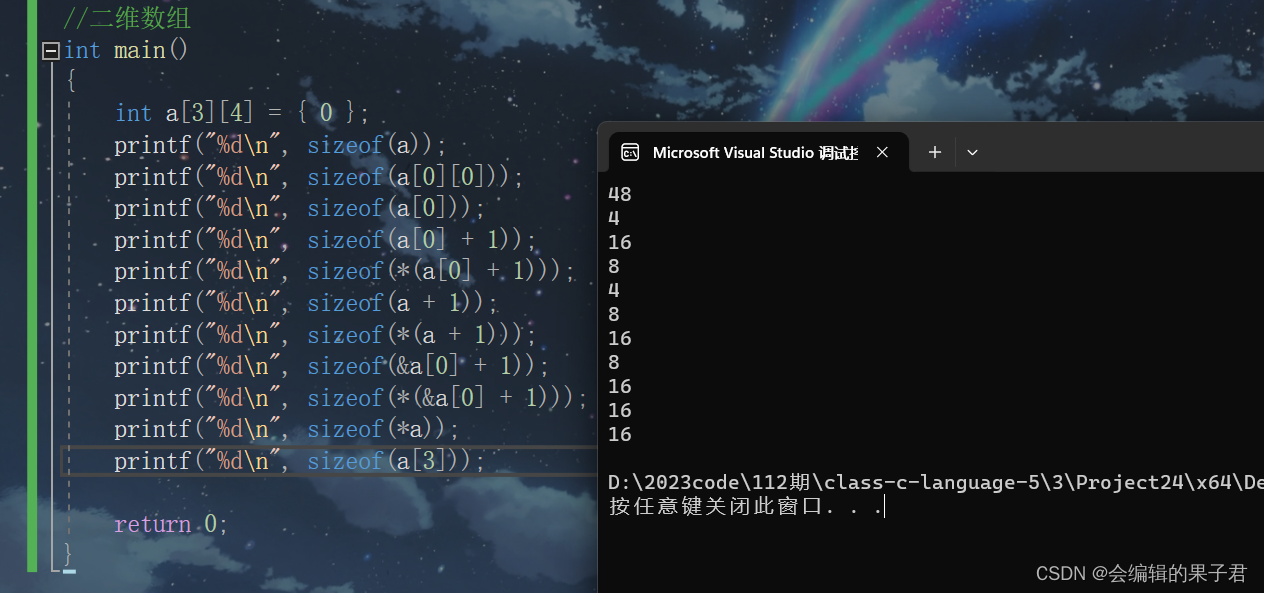
数组笔试题解析(下)
数组面试题解析 字符数组 (一) 我们上一篇文章学习了一维数组的面试题解析内容和字符数组的部分内容,我们这篇文章讲解一下字符数组和指针剩余面试题的解析内容,那现在,我们开始吧。 我们继续看一组字符数组的面试…...
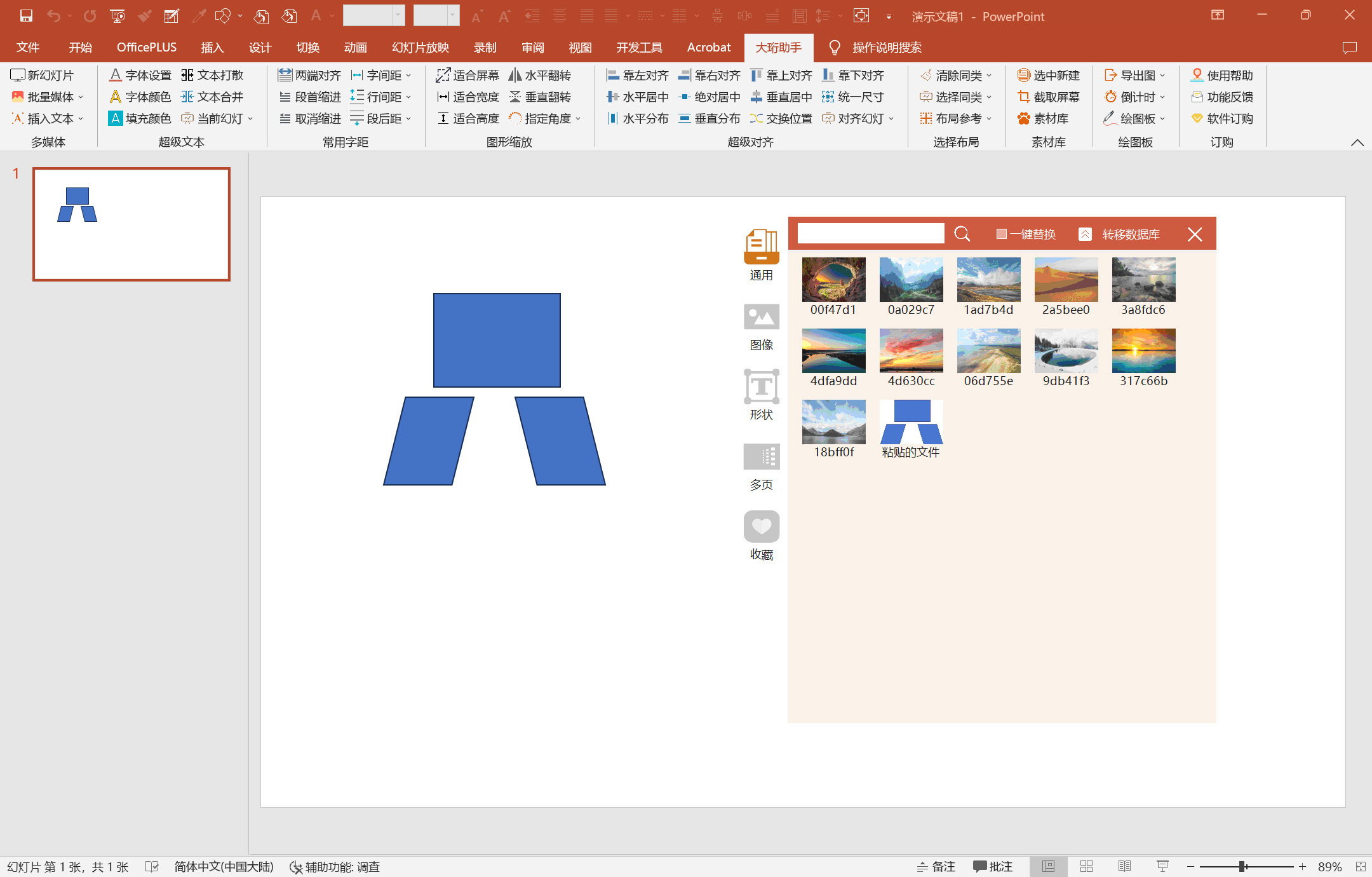
PPT插件-好用的插件-图形缩放-大珩助手
图形缩放 包括适合屏幕、适合宽度、适合高度、水平翻转、垂直翻转、指定角度,可同时对多个形状进行操作 适合屏幕 一键设置图像、文本、形状的长宽尺寸与当前幻灯片一致 适合宽度 一键设置图像、文本、形状的宽度尺寸与当前幻灯片一致 适合高度 一键设置图像…...

五:爬虫-数据解析之xpath解析
五:数据解析之xpath解析 1.xpath介绍: xpath是XML路径语言,它可以用来确定xml文档中的元素位置,通过元素路径来完成对元素的查找,HTML就是XML的一种实现方式,所以xpath是一种非常强大的定位方式 XPa…...

什么是Laravel?它有哪些特性?
Laravel 是一款流行的 PHP Web 框架,设计用于构建现代、优雅且功能强大的 Web 应用程序。它提供了一套丰富的工具和库,以简化常见的开发任务,同时保持灵活性和可扩展性。以下是 Laravel 框架的一些主要特性: 优雅的语法࿱…...
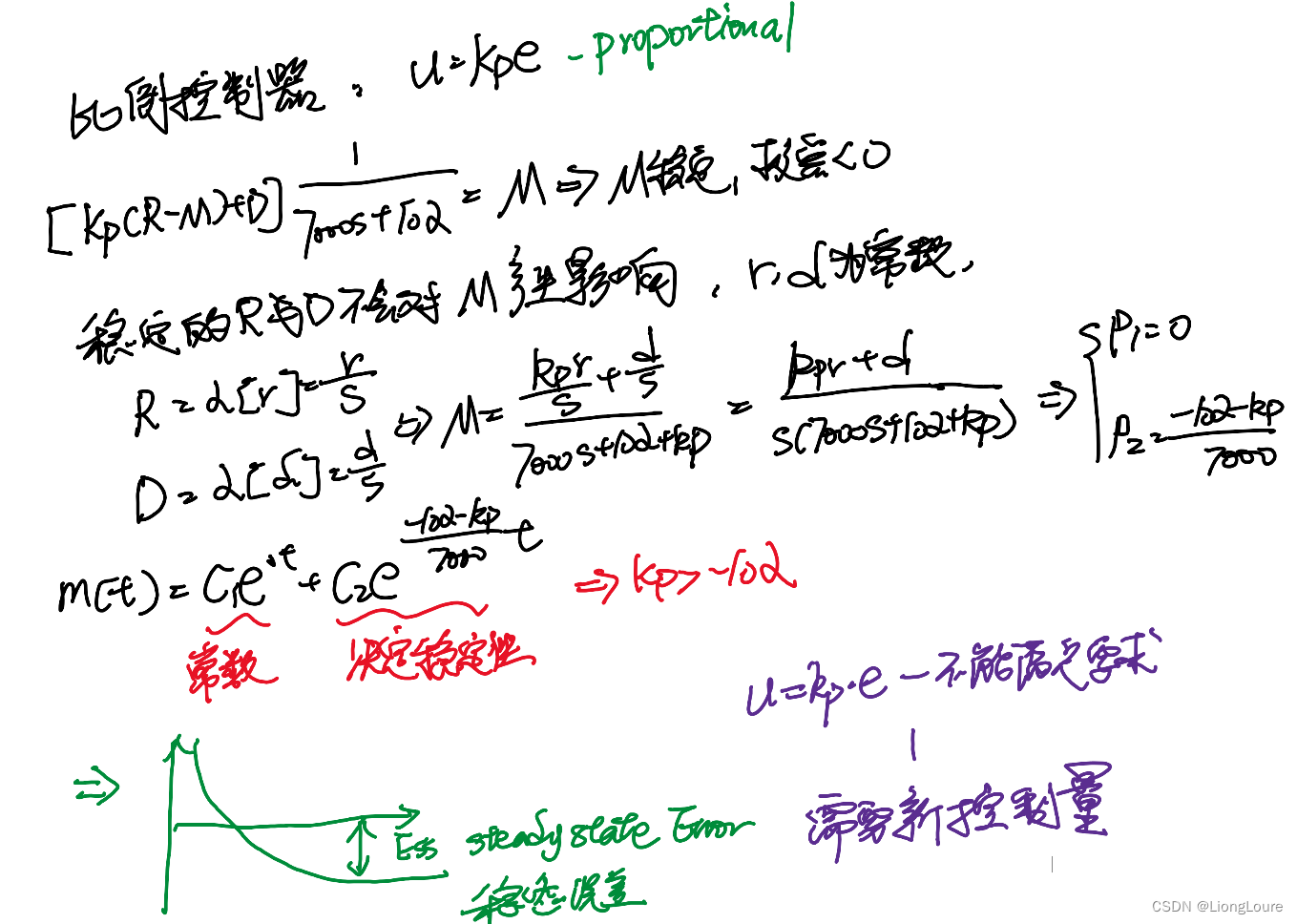
[足式机器人]Part2 Dr. CAN学习笔记-自动控制原理Ch1-3燃烧卡路里-系统分析实例
本文仅供学习使用 本文参考: B站:DR_CAN Dr. CAN学习笔记-自动控制原理Ch1-3燃烧卡路里-系统分析实例 1. 数学模型2. 比例控制 Proprotional Control 1. 数学模型 2. 比例控制 Proprotional Control...
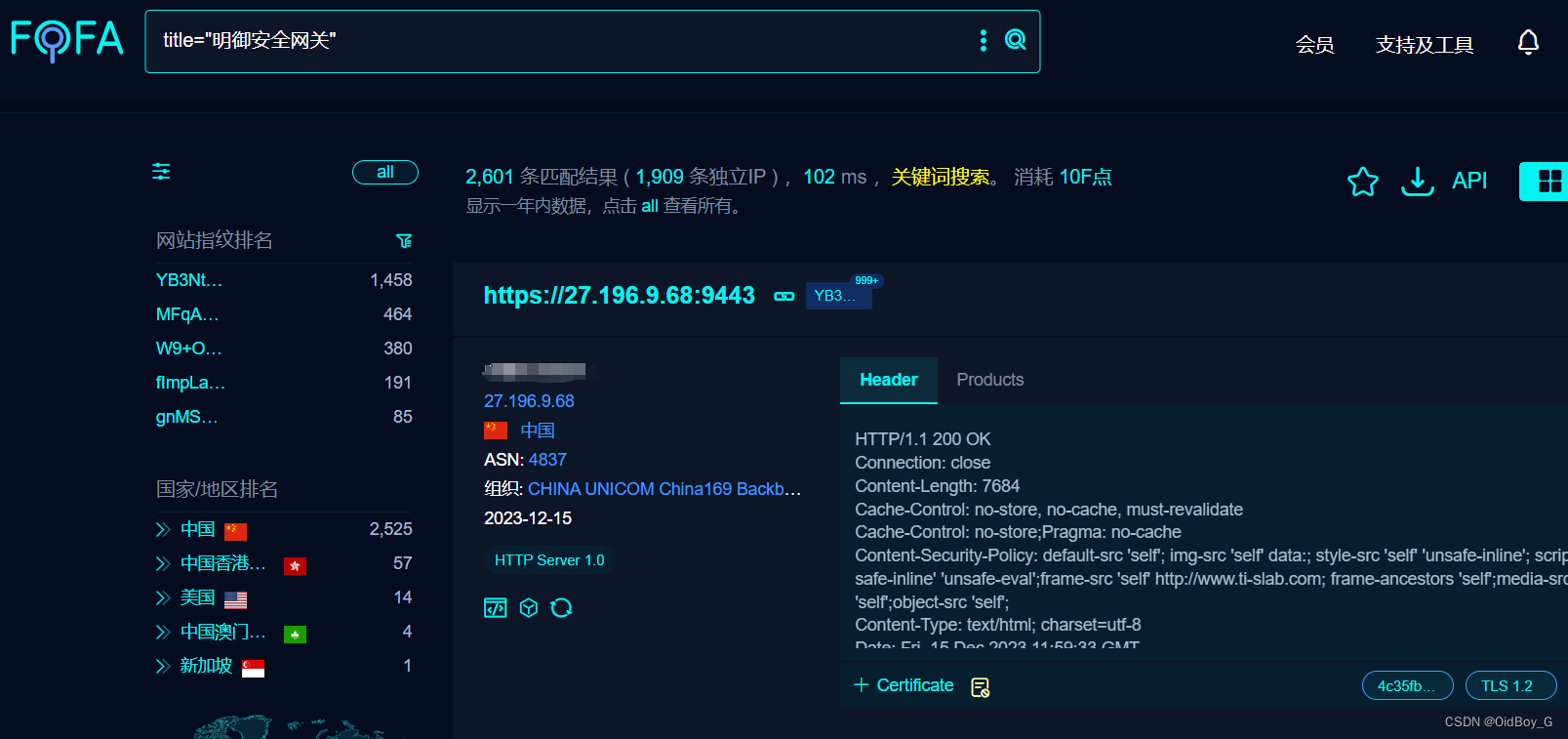
安恒明御安全网关 aaa_local_web_preview文件上传漏洞复现
0x01 产品简介 明御安全网关秉持安全可视、简单有效的理念,以资产为视角,构建全流程防御的下一代安全防护体系,并融合传统防火墙、入侵检测、入侵防御系统、防病毒网关、上网行为管控、VPN网关、威胁情报等安全模块于一体的智慧化安全网关。 0x02 漏洞概述 明御安全网关在…...
基于ssm企业人事管理系统的设计与实现论文
摘 要 进入信息时代以来,很多数据都需要配套软件协助处理,这样可以解决传统方式带来的管理困扰。比如耗时长,成本高,维护数据困难,数据易丢失等缺点。本次使用数据库工具MySQL和编程技术SSM开发的企业人事管理系统&am…...

你知道为什么要加 final 关键字了吗?
嗨,大家好,欢迎来到程序猿漠然公众号,我是漠然。 在Java编程中,我们经常会遇到需要使用final关键字的情况。那么,为什么要使用final关键字呢?它到底有什么作用?本文将从以下几个方面来详细…...
找不到mfc100u.dll,程序无法继续执行?三步即可搞定
在使用电脑过程中,我们经常会遇到一些错误提示,其中之一就是“找不到mfc100u.dll”。mfc100u.dll是Microsoft Foundation Class(MFC)库中的一个版本特定的DLL文件。MFC是微软公司为简化Windows应用程序开发而提供的一套C类库。它包…...
postman接口测试之Postman配置环境变量和全局变量
前言 我们在测试的过程中,遇到最多的问题也可以是环境的问题了吧,今天开发用了这个测试环境,明天又换了另一个测试环境,这样对于我们测试非常的麻烦,特别最接口的时候需要来回的输入环境地址比较麻烦,今天…...

OpenSSL 编程示例
参考:深入探索 OpenSSL:概念、原理、开发步骤、使用方法、使用场景及代码示例 地址:https://oneisall.blog.csdn.net/article/details/131489812?spm1001.2014.3001.5502 目录 1. OpenSSL 概念2. OpenSSL 原理3. OpenSSL 开发步骤4. OpenSSL…...
-k8s核心对象CronJob)
K8S学习指南(17)-k8s核心对象CronJob
文章目录 前言什么是CronJob?示例演示步骤1:创建CronJob步骤2:定义任务模板步骤3:部署CronJob步骤4:监视CronJob的执行 总结 前言 Kubernetes(简称K8s)是一种用于自动部署、扩展和管理容器化应…...
任务调度的介绍)
单片机Freertos入门(二)任务调度的介绍
简介: FreeRTOS支持的任务调度方法有抢占式、协作式、时间片轮转,下面分别来讲解。 1.抢占式调度 抢占式调度,是最高优先级的任务一旦就绪,总能得到CPU的执行权。 高优先级运行时候,低优先级不运行,等待…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...

二叉树-144.二叉树的前序遍历-力扣(LeetCode)
一、题目解析 对于递归方法的前序遍历十分简单,但对于一位合格的程序猿而言,需要掌握将递归转化为非递归的能力,毕竟递归调用的时候会调用大量的栈帧,存在栈溢出风险。 二、算法原理 递归调用本质是系统建立栈帧,而非…...
