Logistic 回归算法
Logistic 回归
- Logistic 回归算法
- Logistic 回归简述
- Sigmoid 函数
- Logistic 回归模型表达式
- 求解参数 $\theta $
- 梯度上升优化算法
- Logistic 回归简单实现
- 使用 sklearn 构建 Logistic 回归分类器
- Logistic 回归算法的优缺点
Logistic 回归算法
Logistic 回归简述
Logistic 回归是一种用于解决二分类问题的机器学习算法。虽然 Logistic Regression 中包含了 Regression 一词,但实际上逻辑回归是一种用于分类的方法,而不是回归。
Logistic 回归通过建立一个逻辑回归模型来预测离散的输出变量,该输出变量可以是 0 或 1。具体来说,该模型基于输入特征的线性组合,通过拟合一个逻辑函数(通常是 sigmoid 函数)将线性组合映射到 [0, 1] 的概率范围内,从而预测输入特征与离散输出变量之间的关系,并将输出映射到 0 或 1 两个不同的类别。
假设现在有一些数据点,我们利用一条直线对这些数据点进行拟合(该直线称为最佳拟合直线),这个拟合过程就称作为回归。如下图所示:

利用逻辑回归模型进行分类的主要思想:根据现有数据,对分类边界建立回归公式,以此进行分类。
Sigmoid 函数
想了解 Logistic 回归,首先需要了解 sigmoid 函数,其公式如下:
f ( x ) = 1 1 + e − x f(x) = \frac{1}{1 + e^{-x}} f(x)=1+e−x1
sigmoid 函数曲线如下图所示:

Logistic 回归模型表达式
逻辑回归模型从本质上来说是一个基于条件概率的判别模型,逻辑回归模型的数学表达式如下:
p ( y = 1 ∣ x ) = 1 1 + e ( − z ) p ( y = 0 ∣ x ) = 1 − p ( y = 1 ∣ x ) p(y=1|x) = \frac{1}{1 + e^{(-z)}} \\ p(y=0|x) = 1 - p(y=1|x) p(y=1∣x)=1+e(−z)1p(y=0∣x)=1−p(y=1∣x)
其中, p ( y = 1 ∣ x ) p(y=1|x) p(y=1∣x) 表示给定输入 x x x 时,输出变量 y = 1 y=1 y=1 的概率, z z z 表示输入特征 x x x 的线性组合加上一个偏置项 b b b,即 z = ∑ i n w i x i + b z = \displaystyle\sum_{i}^{n}w_ix_i + b z=i∑nwixi+b。 w i w_i wi 为特征 x i x_i xi 的权重,通过对训练数据进行最大似然估计或梯度下降等优化,可以确定最佳的权重参数 w w w 和偏置项 b b b。
如果我们把 z z z 展开,那么可以得到如下:
$$
z = \begig{bmatrix} \theta_0
&\theta_1 &\cdots &\theta_n
\end{bmatrix}\begin{bmatrix}x_0
\ x_1
\ \vdots
\ x_n
\end{bmatrix} + b = \theta^Tx + b
$$
h θ ( x ) = g ( θ T x + b ) = g ( z ) = 1 1 + e − z h_\theta(x) = g(\theta^Tx + b) = g(z) = \frac{1}{1 + e^{-z}} hθ(x)=g(θTx+b)=g(z)=1+e−z1
其中, θ \theta θ 是参数列向量(要求解的), x x x 是样本列向量(给定的数据集)。通过 sigmoid 函数可以将任意实数映射到 [0, 1] 区间。 h θ ( x ) h_\theta(x) hθ(x) 给出了输出变量为 1 1 1 的概率,比如 h θ ( x ) = 0.7 h_\theta(x)=0.7 hθ(x)=0.7 表示有 70 % 70\% 70% 的概率判定类别为 1 1 1,有 30 % 30\% 30% 的概率判定类别为 0 0 0。
现在给出一个新的样本,如果我们能找到合适的参数列向量 θ ( [ θ 0 , θ 1 , . . . , θ n ] ) \theta([\theta_0, \theta_1, ..., \theta_n]) θ([θ0,θ1,...,θn]),那么我们就可以将样本数据直接代入 sigmoid 函数中进行求解,得到其类别为 1 1 1 或 0 0 0 的概率,进而判定其所属类别。
求解参数 $\theta $
那么问题来了,我们该如何得到合适的参数向量 θ \theta θ?根据逻辑回归模型的表达式,可以得到如下:
p ( y = 1 ∣ x ; θ ) = h θ ( x ) p ( y = 0 ∣ x ; θ ) = 1 − h θ ( x ) p(y=1|x;\theta) = h_\theta(x) \\ p(y=0|x;\theta) = 1 - h_\theta(x) p(y=1∣x;θ)=hθ(x)p(y=0∣x;θ)=1−hθ(x)
理想状态下,我们希望对每个样本的类别预测概率均为 1 1 1,也就是完全分类正确。但在实际情况中,很难做到如此完美,样本的类别预测概率越接近 1 1 1,其分类结果越准确。一个样本属于正样本的概率为 0.51 0.51 0.51,我们可以说它是正样本;另一个样本属于正样本的概率为 0.99 0.99 0.99,我们也可以说它是正样本;但显然,第二个样本的预测概率更高,更具说服力。我们可以将上述两个类别的条件概率合二为一,得到如下:
L o s s ( h θ ( x ) , y ) = h θ ( x ) y ( 1 − h θ ( x ) ) ( 1 − y ) Loss(h_\theta(x), y) = h_\theta(x)^y(1 - h_\theta(x))^{(1 - y)} Loss(hθ(x),y)=hθ(x)y(1−hθ(x))(1−y)
我们称上式为损失函数(Loss Function)。当 y = 1 y=1 y=1 时,第二项为 0 0 0;当 y = 0 y=0 y=0 时,第一项为 0 0 0。为了简化问题,我们可以对整个表达式进行求对数,得到如下:
L o s s ( h θ ( x ) , y ) = y log h θ ( x ) + ( 1 − y ) log ( 1 − h θ ( x ) ) Loss(h_\theta(x), y) = y \log h_\theta(x) + (1 - y) \log (1 - h_\theta(x)) Loss(hθ(x),y)=yloghθ(x)+(1−y)log(1−hθ(x))
上述损失函数是对于一个样本而言的。假定样本之间相互独立,那么整个样本集的预测概率即为所有样本预测概率的乘积,基于此,可得到如下公式:
J ( θ ) = ∑ i m y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) J(\theta ) = \displaystyle\sum_{i}^{m}y^{(i)}\log (h_\theta(x^{(i)})) + (1 - y^{(i)})\log (1 - h_\theta(x^{(i)})) J(θ)=i∑my(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))
− J ( θ ) = − ∑ i m y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) -J(\theta ) = -\displaystyle\sum_{i}^{m}y^{(i)}\log (h_\theta(x^{(i)})) + (1 - y^{(i)})\log (1 - h_\theta(x^{(i)})) −J(θ)=−i∑my(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))
其中, m m m 为样本总数, y ( i ) y^{(i)} y(i) 表示第 i i i 个样本的类别, x ( i ) x^{(i)} x(i) 表示第 i i i 个样本。由此可以得出,满足 J ( θ ) J(\theta) J(θ) 最大或满足 − J ( θ ) -J(\theta) −J(θ) 最小的 θ \theta θ 值就是我们需要求解的答案。
为了使得 J ( θ ) J(\theta) J(θ) 最大,我们可以使用最大似然估计、梯度上升或梯度下降优化算法求解参数 θ \theta θ。当损失函数为 J ( θ ) J(\theta) J(θ) 时,可以使用梯度上升算法对参数 θ \theta θ 进行优化;当损失函数为 − J ( θ ) -J(\theta) −J(θ) 时,可以使用梯度下降算法对参数 θ \theta θ 进行优化。
梯度上升优化算法
假设存在一个函数 f ( x ) = − x 2 + 4 x f(x) = -x^2 + 4x f(x)=−x2+4x,如何计算该函数的极值?该函数的曲线如下图所示:

显然该函数的曲线开口向下,存在极大值。我们可以运用中学所学的知识对其求极值,其导数为 f ′ ( x ) = − 2 x + 4 f'(x) = -2x + 4 f′(x)=−2x+4,令导数为 0 0 0,可得出 x = 2 x=2 x=2 即为该函数的极大值点,且极大值为 4 4 4。
但在实际情况中,函数不会像上面那样简单,就算求出了函数的导数,也很难精确计算出函数的极值,此时可以考虑用迭代的方法逼近极值。这种通过迭代逼近寻找最佳拟合参数的方法就叫做最优化算法。值更新的公式表示如下:
x i + 1 = x i + α ⋅ ∂ f ( x i ) x i x_{i+1} = x_i + \alpha · \frac{\partial f(x_i)}{x_i} xi+1=xi+α⋅xi∂f(xi)
其中, α \alpha α 为步长,也就是学习率(Learning Rate),用于控制更新的幅度。更新示意图如下所示:

比如从 ( 0 , 0 ) (0, 0) (0,0) 开始,迭代路径为 1 -> 2 -> 3 -> 4 -> ··· -> n,直到求出的 f ( x ) f(x) f(x) 为函数极大值的近似值。迭代逼近函数极大值的代码实现如下:
# 梯度上升
def gradient_ascent(alpha=0.01, precision=0.00000001):""":param alpha: 学习率:param precision: 停止迭代的阈值:return: 逼近函数极值的极值点"""# 偏导表达式def partial_derivative(x_old):return -2 * x_old + 4x_old = -1 # 初始值,给一个小于 x_new 的值x_new = 0 # 梯度上升的起点,即从 (0, 0) 开始while abs(x_new - x_old) > precision:x_old = x_newx_new = x_old + alpha * partial_derivative(x_old)return x_newif __name__ == '__main__':result = gradient_ascent()print(result)
---------
1.999999515279857
从上面可以看出,结果已经非常接近真实极值点 x = 2 x=2 x=2,上述用到的就是梯度上升优化算法。同理, J ( θ ) J(\theta) J(θ) 这个损失函数的极值点也可以这样求出,只要计算出 J ( θ ) J(\theta) J(θ) 的偏导,就可以利用梯度上升算法,求解出 J ( θ ) J(\theta) J(θ) 的极大值。
J ( θ ) J(\theta) J(θ) 关于 θ \theta θ 的偏导,求解过程如下:
∂ J ( θ ) θ j = ∂ J ( θ ) ∂ g ( θ T x ) ∗ ∂ g ( θ T x ) ∂ θ T x ∗ ∂ θ T x ∂ θ j \frac{\partial J(\theta)}{\theta_j} = \frac{\partial J(\theta)}{\partial g(\theta^Tx)} * \frac{\partial g(\theta^Tx)}{\partial \theta^Tx} * \frac{\partial \theta^Tx}{\partial \theta_j} θj∂J(θ)=∂g(θTx)∂J(θ)∗∂θTx∂g(θTx)∗∂θj∂θTx
其中,
∂ J ( θ ) ∂ g ( θ T x ) = y ∗ 1 g ( θ T x ) + ( y − 1 ) ∗ 1 1 − g ( θ T x ) \frac{\partial J(\theta)}{\partial g(\theta^Tx)} = y * \frac{1}{g(\theta^Tx)} + (y - 1) * \frac{1}{1 - g(\theta^Tx)} ∂g(θTx)∂J(θ)=y∗g(θTx)1+(y−1)∗1−g(θTx)1
g ′ ( z ) = d 1 1 + e − z d z = g ( z ) ( 1 − g ( z ) ) ⟹ ∂ g ( θ T x ) ∂ θ T x = g ( θ T x ) ( 1 − g ( θ T x ) ) g'(z) = \frac{d\frac{1}{1 + e^{-z}}}{dz} = g(z)(1-g(z)) \implies \frac{\partial g(\theta^Tx)}{\partial \theta^Tx} =g(\theta^Tx)(1 - g(\theta^Tx)) g′(z)=dzd1+e−z1=g(z)(1−g(z))⟹∂θTx∂g(θTx)=g(θTx)(1−g(θTx))
∂ θ T x θ j = ∂ J ( θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n ) ∂ θ j = x j \frac{\partial \theta^Tx}{\theta_j} = \frac{\partial J(\theta_1x_1 + \theta_2x_2 + \cdots + \theta_nx_n)}{\partial \theta_j} = x_j θj∂θTx=∂θj∂J(θ1x1+θ2x2+⋯+θnxn)=xj
综上可得,
∂ J ( θ ) θ j = ( y − h θ ( x ) ) x j \frac{\partial J(\theta)}{\theta_j} = (y - h_\theta(x))x_j θj∂J(θ)=(y−hθ(x))xj
上述即为 J ( θ ) J(\theta) J(θ) 关于 θ \theta θ 的偏导,有了偏导,我们可以进一步推导出梯度上升中的值更新公式:
θ j _ n e w = θ j _ o l d + α ⋅ ∑ i = 1 m ( y ( i ) − h θ ( x ( i ) ) ) x j ( i ) \theta_{j\_new} = \theta_{j\_old} + \alpha \cdot \displaystyle\sum_{i=1}^{m}(y^{(i)} - h_\theta(x^{(i)}))x_j^{(i)} θj_new=θj_old+α⋅i=1∑m(y(i)−hθ(x(i)))xj(i)
有了上述这些公式,我们就可以编写代码,计算出损失函数的最佳拟合参数。
Logistic 回归简单实现
有一个简单的数据集,其数据格式如下图所示:

该数据集共有三列数据,前两列为特征数据,最后一列为标签数据。我们可以将第一列特征数据看作 x x x 轴上的值,将第二列特征数据看作 y y y 轴上的值,根据对应标签的不同,对这些样本点进行分类。
代码实现如下:
import numpy as np
import matplotlib.pyplot as plt# 读取数据集
def read_dataset(file_path: str) -> (list, list):""":param file_path: 数据集的路径:return: 训练数据,训练标签"""data = [] # 用于存储特征数据;(100, 3);三列分别表示 w0(偏置项)、w1(第一列特征数据权重)、w2(第二列特征数据权重)labels = [] # 用于存储标签数据;(100,)file = open(file_path)for line in file.readlines():line_list = line.strip().split()data.append([1.0, float(line_list[0]), float(line_list[1])])labels.append(int(line_list[2]))file.close()return data, labels# 绘制样本分布图
def data_distribution(data: list, labels: list) -> None:""":param data: 训练数据:param labels: 训练标签:return: 数据分布图"""data_arr = np.array(data) # 转成数组num_samples = data_arr.shape[0] # 获取样本个数x0_feature = [] # 存放标签为 0 的第一列中的特征数据y0_feature = [] # 存放标签为 0 的第二列中的特征数据x1_feature = [] # 存放标签为 1 的第一列中的特征数据y1_feature = [] # 存放标签为 1 的第二列中的特征数据for i in range(num_samples):if labels[i] == 1: # 1 为正样本x1_feature.append(data[i][1])y1_feature.append(data[i][2])else: # 0 为负样本x0_feature.append(data[i][1])y0_feature.append(data[i][2])# 绘图fig = plt.figure()ax = fig.add_subplot(111)ax.scatter(x1_feature, y1_feature, s=20, c='r', marker='s', alpha=.5)ax.scatter(x0_feature, y0_feature, s=20, c='g', alpha=.5)plt.title('data distribution')plt.xlabel('x')plt.ylabel('y')plt.show()# sigmoid 函数
def sigmoid(z):""":param z: 目标值表达式:return: sigmoid 表达式"""return 1.0 / (1 + np.exp(-z))# 梯度上升
def gradient_ascent(data: list, labels: list, alpha=0.001, num_iteration=500) -> np.ndarray:""":param data: 训练数据:param labels: 训练标签:param alpha: 学习率:param num_iteration: 迭代次数:return: 参数权重"""data_mat = np.mat(data) # 转成矩阵labels_mat = np.mat(labels).transpose() # 转成矩阵,并进行转置n = data_mat.shape[1] # data 的列数;3weights = np.ones((n, 1)) # 有几个特征就有几个参数,这里有 3 个特征,因此有 3 个参数# 训练模型,得到参数权重for i in range(num_iteration):h = sigmoid(data_mat * weights) # 预测值;(100, 1)error = labels_mat - h # 真实值 - 预测值;(100, 1)weights = weights + alpha * data_mat.transpose() * error # w_new = w_old + α * x^T * (y - y')return weights.getA() # 将矩阵转换为数组,并返回权重数组# 通过求解出的参数(回归系数),可以确定不同类别数据之间的分隔线,从而绘制出决策边界
def decision_boundary(data: list, labels: list, weights: np.ndarray) -> None:""":param data: 训练数据:param labels: 训练标签:param weights: 参数权重:return: 决策边界图"""data_arr = np.array(data) # 转成数组num_samples = data_arr.shape[0] # 获取样本个数x0_feature = [] # 存放标签为 0 的第一列中的特征数据y0_feature = [] # 存放标签为 0 的第二列中的特征数据x1_feature = [] # 存放标签为 1 的第一列中的特征数据y1_feature = [] # 存放标签为 1 的第二列中的特征数据for i in range(num_samples):if labels[i] == 1: # 1 为正样本x1_feature.append(data[i][1])y1_feature.append(data[i][2])else: # 0 为负样本x0_feature.append(data[i][1])y0_feature.append(data[i][2])# 绘图fig = plt.figure()ax = fig.add_subplot(111)ax.scatter(x1_feature, y1_feature, s=20, c='r', marker='s', alpha=.5)ax.scatter(x0_feature, y0_feature, s=20, c='g', alpha=.5)x = np.arange(-3.0, 3.0, 0.1)y = -(weights[0] + weights[1] * x) / weights[2]ax.plot(x, y)plt.title('best fit')plt.xlabel('x1')plt.ylabel('x2')plt.show()if __name__ == '__main__':file_path = r'D:\MachineLearning\testSet.txt'# 获取训练数据和训练标签data, labels = read_dataset(file_path)# 查看样本分布# data_distribution(data, labels)# 获取权重weights = gradient_ascent(data, labels) # 得到一个形状为 (3, 1) 的权重数组print(weights)# 查看决策边界decision_boundary(data, labels, weights)"""
weights 是一个包含三个元素的数组 [w0, w1, w2],其中 w0 是偏置项(或者称为截距),w1 和 w2 分别是特征一和特征二的权重;
在二维空间中,线性分类器的决策边界通常是一条直线,其方程可以表示为 w0 + w1*x1 + w2*x2 = 0,其中 (x1, x2) 是特征一和特征二的取值;
将上述方程稍作变换,就可以得到 - (w0 + w1*x) / w2,其中 x = x1,也就是特征一的取值。这个表达式描述了特征一和特征二之间的决策边界,可以用来在二维平面上画出分类器的决策边界直线。
"""
---------
[[ 4.12414349][ 0.48007329][-0.6168482 ]]

上述代码在进行梯度上升优化时,每次都需要计算整个数据集,计算复杂度太高,我们可以使用随机梯度上升算法对其进行改进。主要改进有两点,第一点是动态调整学习率,使得学习率随着迭代次数的增加而减小;第二点是使用一个样本数据进行参数的更新,样本数据随机选取,且下一次迭代将从未使用过的样本点中选取。随机梯度上升算法可以有效地减少计算量,并保证回归效果。
经过综合对比,我们可以得到以下结论:
- 当数据集较小时,使用梯度上升算法效果较好
- 当数据集较大时,使用改进的随机梯度上升算法效果较好
使用 sklearn 构建 Logistic 回归分类器
sklearn.linear_model 模块实现了 Logistic 回归算法,不仅如此,该模块还提供了很多模型供我们使用,比如 Lasso 回归、脊回归等。LogisticRegression 函数实现如下所示:
sklearn.linear_model.LogisticRegression(penalty='l2', dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver='lbfgs', max_iter=100, multi_class='auto', verbose=0, warm_start=False, n_jobs=None, l1_ratio=None)- penalty:有 l1、l2、elasticnet、None 四个值可供选择,默认为 l2;l1 表示添加 l1 正则化,假设模型的参数满足拉普拉斯分布;l2 表示添加 l2 正则化,假设模型的参数满足高斯分布;elasticnet 表示添加 l1 和 l2 正则化;None 表示不添加正则项;所谓的正则项就是对参数施加一种约束,使得模型避免发生过拟合的现象,但是不一定加约束就更好,只能说在加约束的情况下,理论上应该可以获得泛华能力更强的结果- dual:布尔值,默认为 False;二元公式仅适用于 liblinear 求解器的 l2 惩罚,当 n_samples > n_features 时,首选 dual=False- tol:停止求解的标准,即求解到多少认为已经求出最优解,默认为 1e-4;- C:正则化强度的倒数,必须是正浮点数,默认为 1.0;与 SVM 一样,数值越小,正则化强度越大- fit_intercept:是否存在截距或偏差,即偏置项,默认为 True- intercept_scaling:只有在使用求解器 liblinear 且 fit_intercept=True 时才有用,默认为 1- class_weight:用于标示分类模型中各种类型的权重,可以是一个字典或 balanced 字符串,默认为 None;举个例子,对于 0、1 的二元模型,我们可以定义 class_weight={0: 0.9, 1: 0.1},这样类型 0 的权重为 90%,而类型 1 的权重为 10%;如果 class_weight 选择 balanced,那么类库会根据训练样本量来计算权重,某种类型样本量越多,则权重越低,样本量越少,则权重越高,类权重计算方法为 n_samples / (n_classes * np.bincount(y)),n_samples 为样本数,n_classes 为类别数量,np.bincount(y) 会输出每个类的样本数,例如 y=[1, 0, 0, 1, 1],则 np.bincount(y)=[2, 3]- random_state:随机数种子,默认为 None;仅在 solver 为 sag、saga、liblinear 时有用- solver:优化算法,默认为 lgfgs;对于小数据集,liblinear 是个不错的选择,而对于大数据集,sag 和 saga 速度更快;对于多分类问题,只有 newton-cg、sag、saga、lbfgs 能够处理多项式损失,而 liblinear 受限于一对剩余(OvR),就是用 liblinear 的时候,如果是多分类问题,得先把一种类别作为一个类别,剩余的所有类别作为另外一个类别,依次类推,遍历所有类别,从而进行分类;newton-cg、sag、lbfgs 这三种优化算法都需要损失函数的一阶或者二阶连续导数,因此不能用于没有连续导数的 L1 正则化,只能用于 L2 正则化,而 liblinear 和 saga 通吃 L1 和 L2 正则化;liblinear 使用了开源的 liblinear 库,内部使用了坐标轴下降法来迭代优化损失函数;lbfgs 是拟牛顿法的一种,利用损失函数二阶导数矩阵(即海森矩阵)来迭代优化损失函数;newton-cg 是牛顿法家族中的一种,利用海森矩阵来迭代优化;sag 是随机平均梯度下降,属于梯度下降法的变种,与普通梯度下降法的区别是每次迭代仅用一部分样本来计算梯度,适用于样本量多的情况;saga 是线性收敛的随机优化算法的变种- max_iter:算法收敛的最大迭代次数,默认为 100- multi_class:分类方式,有 auto、ovr、multinomial 可供选择,默认为 auto;如果选择的是 ovr,那么每个标签都会拟合出一个二元问题;当求解器为 liblinear 时,multinomial 不可用;如果数据是二元的,或者求解器为 liblinear,auto 会选择 ovr,其他情况则选择 multinomial- verbose:日志冗长度,默认为 0,即不输出训练过程;为 1 的时候偶尔输出结果;大于 1 时对每个子模型都输出结果- warm_start:热启动参数,默认为 False;如果为 True,则下一次训练以追加树的形式进行- n_jobs:并行数,默认为 1;如果为 2,则表示用 CPU 的 2 个内核运行程序;如果为 -1,则表示用所有内核运行- l1_ratio:elasticnet 的混合参数,仅在 penalty=elasticnet 时使用;如果为 0,则表示使用 l2 正则化
由 LogisticRegression 创建的实例对象 clf 具有以下方法:
decision_function(X) # 预测样本的置信度得分- X:训练数据,形状为 (n_samples, n_features)返回形状为 (n_samples, n_classes) 的置信度得分densify() # 将系数矩阵转换为密集数组格式fit(X, y, sample_weight=None) # 根据训练集拟合分类器- X:训练数据,形状为 (n_samples, n_features)- y:目标值(训练样本对应的标签),形状为 (n_samples,)- sample_weight:样本权重,如果为 None,则样本权重相同返回拟合的逻辑回归分类器get_params(deep=True) # 以字典形式返回 MultinomialNB 类的参数- deep:布尔值,默认为 True返回参数predict(X) # 预测所提供数据的类别标签- X:预测数据,形状为 (n_samples, n_features)以 np.ndarray 形式返回形状为 (n_samples,) 的每个数据样本的类别标签predict_log_proba(X) # 返回预测数据 X 在各类别标签中所占的对数概率- X:预测数据,形状为 (n_samples, n_features)返回该样本在各类别标签中的预测对数概率,类别的顺序与属性 classes_ 中的顺序一致predict_proba(X) # 返回预测数据 X 在各类别标签中所占的概率- X:预测数据,形状为 (n_samples, n_features)返回该样本在各类别标签中的预测概率,类别的顺序与属性 classes_ 中的顺序一致score(X, y, sample_weight=None) # 返回预测结果和标签之间的平均准确率- X:预测数据,形状为 (n_samples, n_features)- y:预测数据的目标值(真实标签)- sample_weight:默认为 None返回预测数据的平均准确率,相当于先执行了 self.predict(X),而后再计算预测值和真实值之间的平均准确率
from sklearn.linear_model import LogisticRegressiondef colicSklearn():frTrain = open(r'D:\MachineLearning\horseColicTraining.txt') # 打开训练集frTest = open(r'D:\MachineLearning\horseColicTest.txt') # 打开测试集trainingSet = []trainingLabels = []testSet = []testLabels = []for line in frTrain.readlines():currLine = line.strip().split('\t')lineArr = []for i in range(len(currLine) - 1):lineArr.append(float(currLine[i]))trainingSet.append(lineArr)trainingLabels.append(float(currLine[-1]))for line in frTest.readlines():currLine = line.strip().split('\t')lineArr = []for i in range(len(currLine) - 1):lineArr.append(float(currLine[i]))testSet.append(lineArr)testLabels.append(float(currLine[-1]))classifier = LogisticRegression(solver='liblinear', max_iter=10).fit(trainingSet, trainingLabels)test_accurcy = classifier.score(testSet, testLabels) * 100print('正确率:%f%%' % test_accurcy)if __name__ == '__main__':colicSklearn()
---------
正确率:73.134328%
Logistic 回归算法的优缺点
优点
- 算法简单易于理解和实现,计算效率高。
- 可以处理二分类和多分类问题。
- 对特征之间的关联性不敏感,适用于处理高维数据。
- 输出结果具有概率解释,可以用于判断样本属于某个类别的概率。
缺点
- 假设特征与目标变量之间存在线性关系,无法处理非线性关系。
- 对异常值和缺失值比较敏感,需要进行数据预处理。
- 容易出现欠拟合或过拟合的情况,需要进行正则化处理。
- 无法处理特征之间的交互作用。
相关文章:

Logistic 回归算法
Logistic 回归 Logistic 回归算法Logistic 回归简述Sigmoid 函数Logistic 回归模型表达式求解参数 $\theta $梯度上升优化算法 Logistic 回归简单实现使用 sklearn 构建 Logistic 回归分类器Logistic 回归算法的优缺点 Logistic 回归算法 Logistic 回归简述 Logistic 回归是一…...
ubuntu安装详细步骤
一,先下载vmware 1,第一步打开上面链接 下载网址 : https://www.vmware.com/products/workstation-pro/wo rkstation-pro-evaluation.html 许可证 JU090-6039P-08409-8J0QH-2YR7F ZF3R0-FHED2-M80TY-8QYGC-NPKYF FC7D0-D1YDL-M8DXZ-CYPZE-P2AY6 ZC3T…...

力扣5. 最长回文子串
动态规划 思路: 假设 dp[i][j] 为字符串 (i, j) 子串是否为回文的结果;那么 dp[i][j] dp[i 1][j - 1] 且 (s[i] s[j]);长度为1的字符串都是回文; 原字符串长度为1,是回文;原字符串子串长度为1ÿ…...

肆[4],函数VectorToHomMat2d/AffineTransPoint2d
函数VectorToHomMat2d C形式 LIntExport void VectorToHomMat2d( const HTuple& Px, const HTuple& Py, const HTuple& Qx, const HTuple& Qy, HTuple* HomMat2D);//参数1:图像坐标X数组 //参数2:图像坐标Y数组 //参数3:世界坐标X数组 //参数4:世界坐标Y…...

下载文件 后端返回给前端 response header 响应头
当浏览器在请求资源时,会通过http返回头中的content-type决定如何显示/处理将要加载的数据,如果这个类型浏览器能够支持阅览,浏览器就会直接展示该资源,比如png、jpeg、video等格式。在某些下载文件的场景中,服务端可能…...
lvs负载均集群
目录 NAT模式 LVS负载均衡群集部署 1.部署共享存储 2.配置节点服务器 192.168.17.130 编辑 192.168.17.133 3.配置负载调度器 4.测试效果 NAT模式 LVS负载均衡群集部署 负载调度器:内网关 ens33:192.168.17.70,外网关 ens36&#x…...
luttuce(RedisTempate)实现hash expire lua脚本
话不多说先放脚本: local argv ARGV local length #argv if length > 0 then local unpackArgs {} for i 1, length - 1 dotable.insert(unpackArgs, argv[i]) end if redis.call(exists, KEYS[1]) 1 thenredis.call(del, KEYS[1])redis.call(hset, KEYS[…...

【Xamarin】WebView连接局域网自动跳转外部浏览器问题的解决
xamarin在中国用的很少,但也有一些独到之处。例如用惯了Visual Studio的就很合适。而且类Java开发,几乎没什么障碍。 protected override void OnCreate(Bundle savedInstanceState) {base.OnCreate(savedInstanceState);Xamarin.Essentials.Platform.I…...
【Unity动画】实现不同的肢体动作自由搭配播放Layer+Avatar Mask
这个教程教你学会使用Unity 动画层配合布偶遮罩(AvaterMask) 实现从2个动画身上只保留部分肢体动作,然后搭配播放 例如:一个正常跑的动画片段,我只保留腿部动作,形成一个层叫Run_leg 然后在从一个攻击动作…...
转换为二进制)
将0x06(16进制)转换为二进制
将0x06(16进制)转换为二进制,可以按照如下步骤进行: 1. 将0x06中的字母"0x"去除。 2. 将数字"06"中的数字"0"去除。 3. 将数字"06"转换为二进制。 根据步骤1和步骤2,去除&q…...

考PRINCE2有用么?有PMP证书了还需要考PRINCE2吗?
有用的,PMP相当于是理论,PRINCE2是实践,对小白来说pmp考后再考一个prince2是很好的选择,对项目管理的小白来说更好入门。 先来说下 prince 2 和 pmp 的区别 一、prince 2 是什么?跟PMP有什么区别? prince…...

06进程间关系-学习笔记
Orphan Process孤儿进程 父进程先于子进程退出,子进程失去托管,这种子进程统称为孤儿进程 失效进程(孤儿进程):导致内存泄漏,影响新进程的创建孤儿进程的危害不可预测,如果一个孤儿进程持续的申…...

Vue的动画方式有几种
Vue的动画方式有几种? Vue的动画方式主要分成两大类,一类是CSS动画,一类是JS动画 CSS动画中包含transition以及animation,但在Vue中只需要通过transition封装组件实现。 CSS动画的类名主要包括:v-enter、v-enter-acti…...

PyTorch: 基于【VGG16】处理MNIST数据集的图像分类任务【准确率98.9%+】
目录 引言在Conda虚拟环境下安装pytorch步骤一:利用代码自动下载mnist数据集步骤二:搭建基于VGG16的图像分类模型步骤三:训练模型步骤四:测试模型运行结果后续模型的优化和改进建议完整代码结束语 引言 在本博客中,小…...
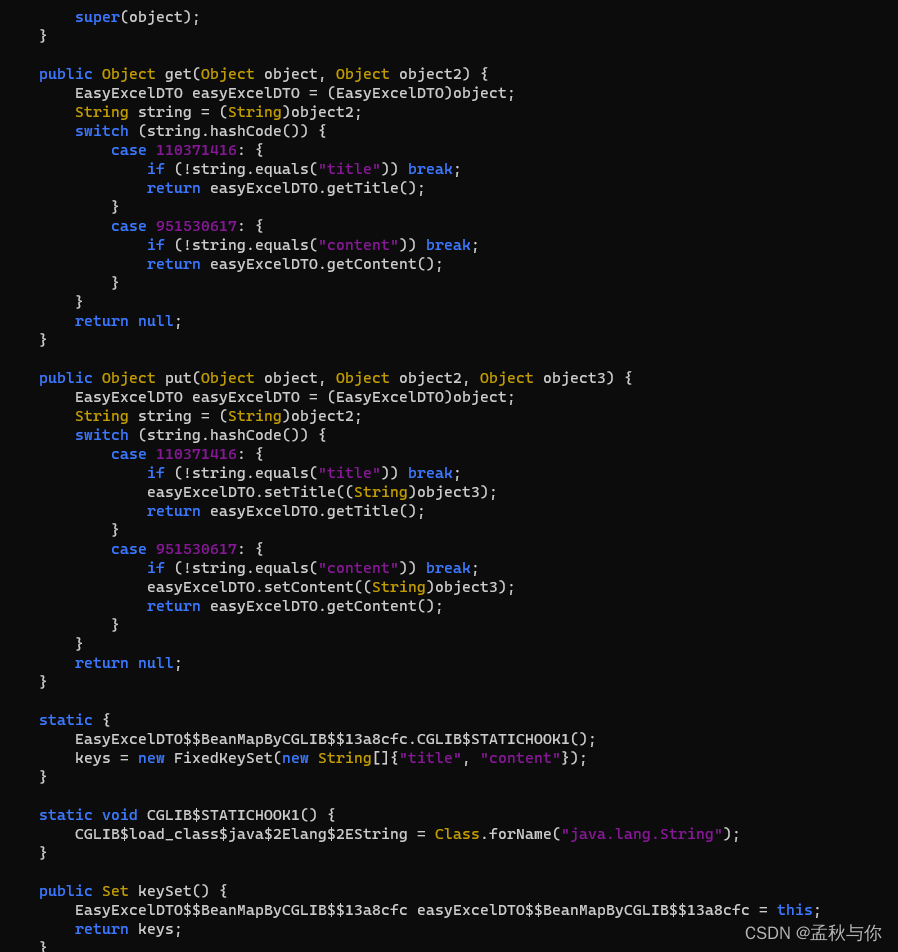
【lombok】从easyExcel read不到值到cglib @Accessors(chain = true)隐藏的大坑
背景: 在一次使用easyExcel.read 读取excel时,发现实体类字段没有值,在反复测试后,发现去掉Accessors(chain true)就正常了,为了验证原因,进行了一次代码跟踪 由于调用链路特别长,只列举出部分代码&#x…...

1-SaaS通识
云计算 讲SaaS必须先讲云计算。云计算通过互联网提供计算服务,包括服务器、存储、数据库、网络、应用等,采用按需付费的定价模式。 云计算的4种部署模式 公有云:由云服务商拥有和管理,就好比水电,居民共享ÿ…...

Spring Boot实现接口幂等
Spring Boot实现接口幂等 1、pom依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http:…...
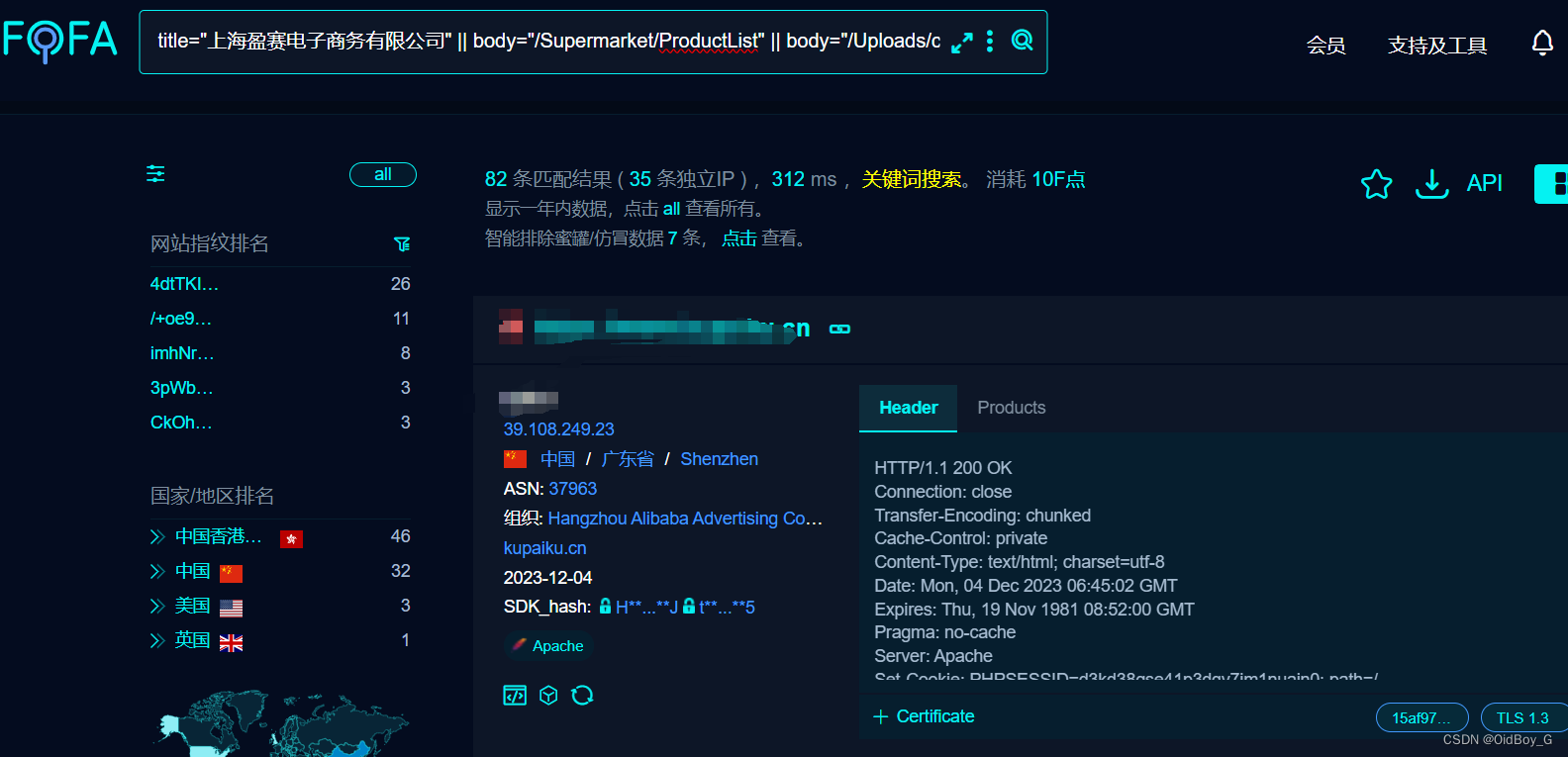
ShopsN commentUpload 文件上传漏洞复现
0x01 产品简介 ShopsN 是一款符合企业级商用标准全功能的真正允许免费商业用途的开源网店全网系统。 0x02 漏洞概述 ShopsN commentUpload 接口处存在任意文件上传漏洞,攻击者可以利用文件上传漏洞执行恶意代码、写入后门、读取敏感文件,从而可能导致服务器受到攻击并被控…...

【Qt5】ui文件最后会变成头文件
2023年12月14日,周四下午 我也是今天下午偶然间发现这个的 在使用Qt的uic(User Interface Compiler)工具编译ui文件时,会生成对应的头文件。 在Qt中,ui文件是用于描述用户界面的XML文件,而头文件是用于在…...
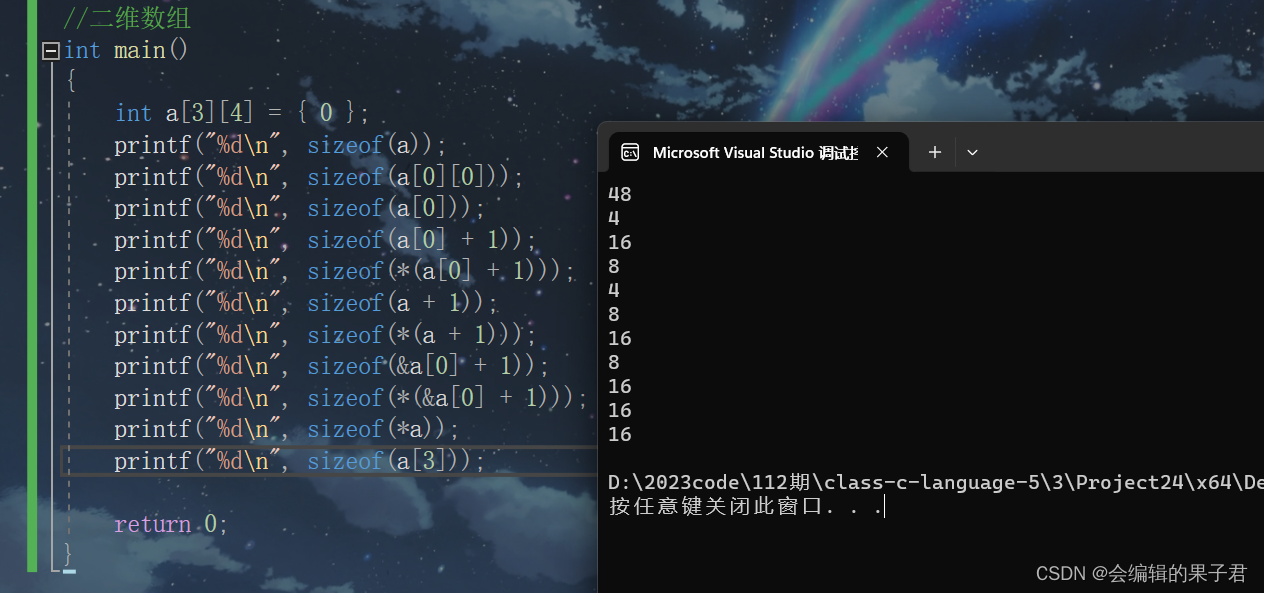
数组笔试题解析(下)
数组面试题解析 字符数组 (一) 我们上一篇文章学习了一维数组的面试题解析内容和字符数组的部分内容,我们这篇文章讲解一下字符数组和指针剩余面试题的解析内容,那现在,我们开始吧。 我们继续看一组字符数组的面试…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...
