D34|不同路径
62.不同路径
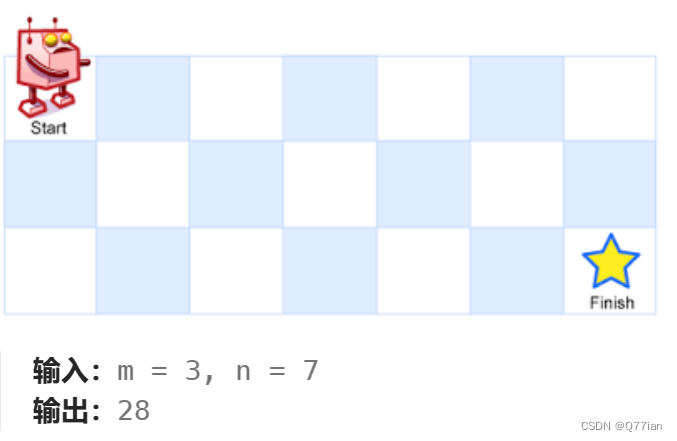
初始思路:
1)确定dp数组以及下标的含义:
dp[i][i]存放到第i+1行和第i+1列的方法数
2)确定递推公式:
dp[i][i] = dp[i -1][i] + dp[i][i-1]
3)dp数组如何初始化
第0行是1;
第0列是1;
4)确定遍历顺序
从前到后
5)举例推导dp数组
class Solution {public int uniquePaths(int m, int n) {int[][] dp = new int[m][n];for(int i = 0;i<m;i++){dp[i][0] = 1;}for(int i = 0;i<n;i++){dp[0][i] = 1;}for(int i =1;i<m;i++){for(int j = 1;j<n;j++){dp[i][j] = dp[i][j-1] + dp[i-1][j];}}return dp[m-1][n-1];}
}题解复盘:
基本一致 。
63. 不同路径 II
初始思路:
在前一题的基础之上增加了对障碍数组的判断,如果第一行中有一个障碍,那么这个障碍后面的dp全部赋值为0,前面的都赋值为1;列同理。
再过程中遇到障碍,令当前dp为0即可。
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;int[][] dp = new int[m][n];for(int i = 0;i<m;i++){if(obstacleGrid[i][0]==1){break;}dp[i][0] = 1;}for(int i = 0;i<n;i++){if(obstacleGrid[0][i]==1){break;}dp[0][i] = 1;}for(int i =1;i<m;i++){for(int j = 1;j<n;j++){if(obstacleGrid[i][j]==1){dp[i][j] = 0;}else{dp[i][j] = dp[i][j-1] + dp[i-1][j];}}}return dp[m-1][n-1];}
}
相关文章:

D34|不同路径
62.不同路径 初始思路: 1)确定dp数组以及下标的含义: dp[i][i]存放到第i1行和第i1列的方法数 2)确定递推公式: dp[i][i] dp[i -1][i] dp[i][i-1] 3)dp数组如何初始化 第0行是1; 第0列是1&a…...
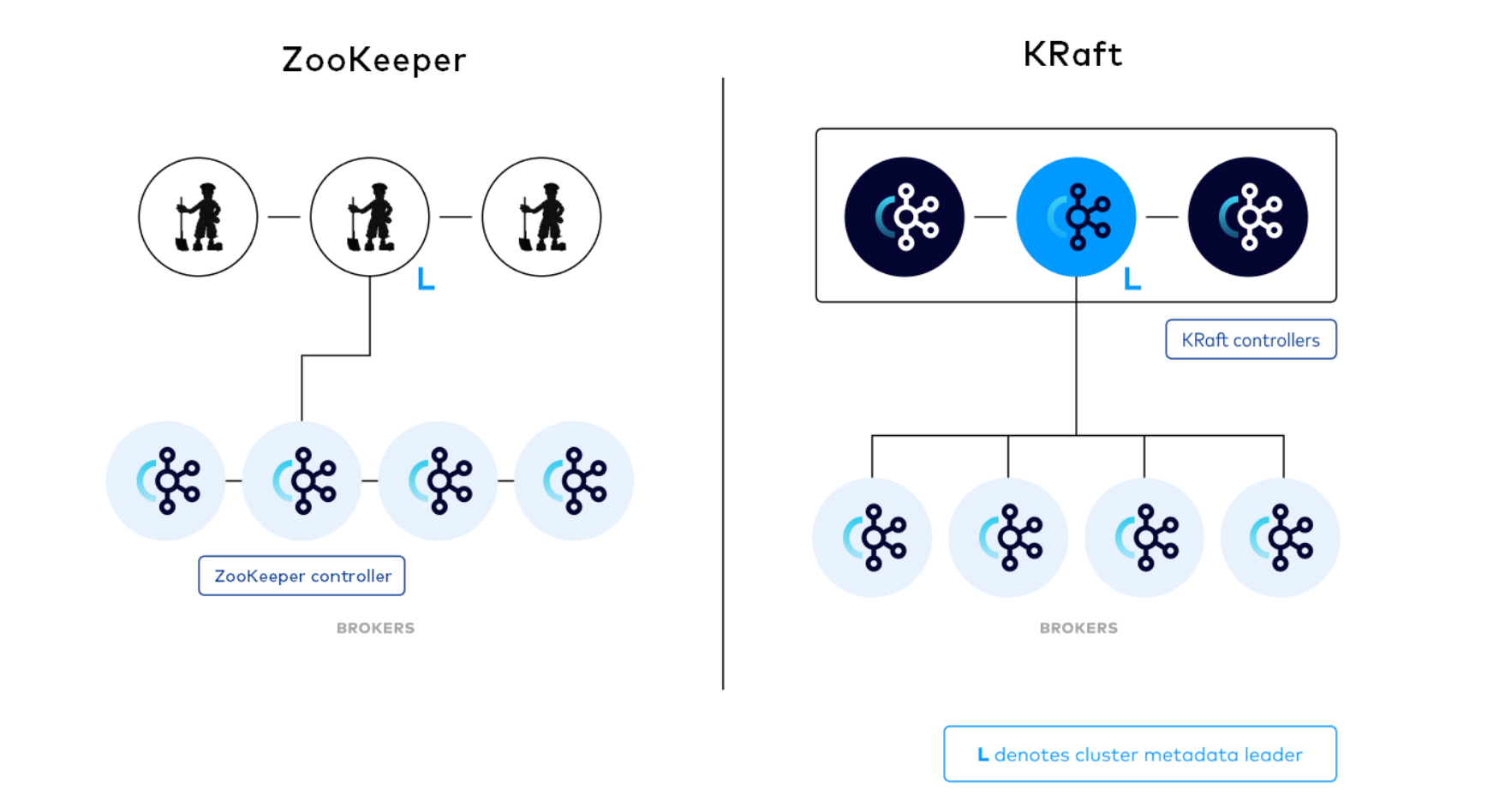
【运维】Kafka高可用: KRaft(不依赖zookeeper)集群搭建
文章目录 一. kafka kraft 集群介绍1. KRaft架构2. Controller 服务器3. Process Roles4. Quorum Voters5. kraft的工作原理 ing 二. 集群安装1. 安装1.1. 配置1.2. 格式化 2. 启动测试2.1. 启功节点服务2.2. 测试 本文主要介绍了 kafka raft集群架构: 与旧架构的不…...

Python 自动化之批量处理文件(一)
批量新建目录、文档Pro版本 文章目录 批量新建目录、文档Pro版本前言一、做成什么样子二、基本思路1.引入库2.基本架构 三、用户输入模块四、数据处理模块1.excel表格数据获取2.批量数据的生成 总结 前言 我来写一个不一样的批量新建吧。在工作中,有些同学应该会遇…...

力扣72. 编辑距离
动态规划 思路: 假设 dp[i][j] 是 word1 前 i 个字母到 word2 前 j 个字母的编辑距离;那么状态 dp[i][j] 状态的上一个状态有: dp[i - 1][j],word1 前 i - 1 个字母到 word2 前 j 个字母的编辑距离,此状态再插入一个字…...
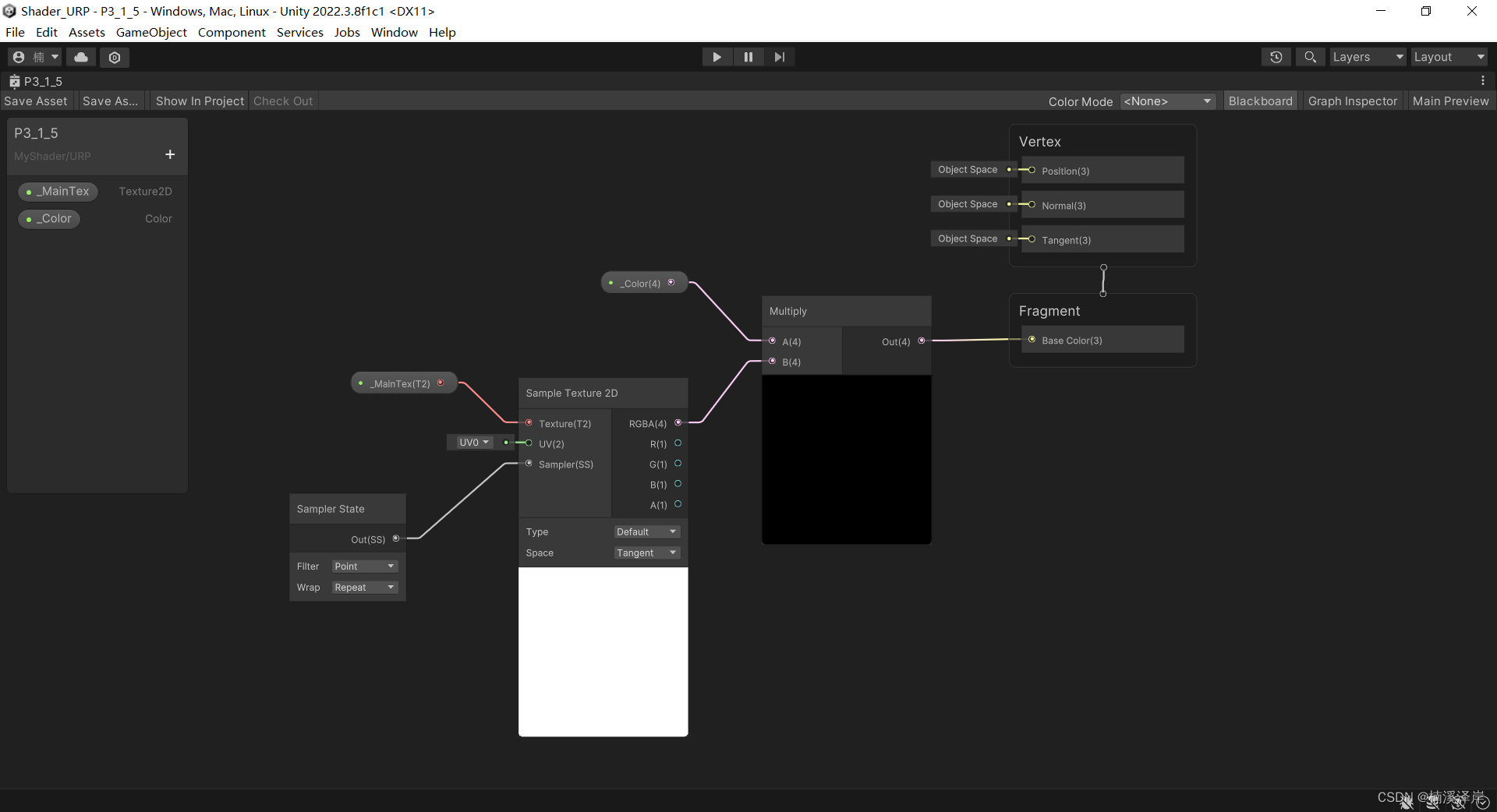
Unity中 URP Shader 的纹理与采样器的分离定义
文章目录 前言一、URP Shader 纹理采样的实现1、在属性面板定义一个2D变量用于接收纹理2、申明纹理3、申明采样器4、进行纹理采样 二、申明纹理 和 申明采样器内部干了什么1、申明纹理2、申明采样器 三、采样器设置采样器的传入格式1、纹理设置中,可以看见我们的采样…...

Electron学习第一天 ,启动项目
之前在安装官网的步骤操作,结果报错,找了好多办法,最后这种办法成功启动项目,并且没有报错,特此记录 特别提醒,最好安装淘宝镜像,npm 太慢,会导致报错问题,解决起来个人觉…...

WebService技术--随笔1
1.WebService 发展史 创建阶段(1990 年代末至 2000 年代初):在这个阶段,XML-RPC 和 SOAP 协议被引入,为跨平台和跨语言的应用程序集成提供了基础。XML-RPC 提供了一种基于 XML 的远程过程调用机制,而 SOAP…...

如何使用Docker将.Net6项目部署到Linux服务器(一)
目录 一 配置服务器环境 1.1 配置yum 1.1.1 更新yum包 1.1.2 yum命令 1.2 配置docker …...

第4章-第3节-Java中跟数组相关的几个算法以及综合应用
在写这篇博文之前,先大概说明一下,就是很常见的数组算法如求最大值、一维数组的遍历等,这里就不去专门说明了,只说一些有代表性的,然后就是冒泡排序算法很容易查阅到,这里也不专门说明了,只说明…...
AlexNet(pytorch)
AlexNet是2012年ISLVRC 2012(ImageNet Large Scale Visual Recognition Challenge)竞赛的冠军网络,分类准确率由传统的 70%提升到 80% 该网络的亮点在于: (1)首次利用 GPU 进行网络加速训练。 ÿ…...

【单调栈 】LeetCode321:拼接最大数
作者推荐 【动态规划】【广度优先搜索】LeetCode:2617 网格图中最少访问的格子数 本文涉及的知识点 单调栈 题目 给定长度分别为 m 和 n 的两个数组,其元素由 0-9 构成,表示两个自然数各位上的数字。现在从这两个数组中选出 k (k < m n) 个数字…...

TikTok与虚拟现实的完美交融:全新娱乐时代的开启
TikTok,这个风靡全球的短视频平台,与虚拟现实(VR)技术的深度结合,为用户呈现了一场全新的娱乐盛宴。虚拟现实技术为TikTok带来了更丰富、更沉浸的用户体验,标志着全新娱乐时代的开启。本文将深入探讨TikTok…...

PXI/PCIe/VPX机箱 ARM|x86 + FPGA测试测量板卡解决方案
PXI便携式测控系统是一种基于PXI总线的便携式测试测控系统,它填补了现有台式及机架式仪器在外场测控和便携测控应用上的空白,在军工国防、航空航天、兵器电子、船舶舰载等各个领域的外场测控场合和科学试验研究场合都有广泛的应用。由于PXI便携式测控系统…...

ES6 面试题 | 12.精选 ES6 面试题
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

【linux】Debian不能运行sudo的解决
一、问题: sudo: 没有找到有效的 sudoers 资源,退出 sudo: 初始化审计插件 sudoers_audit 出错 二、可用的方法: 出现 "sudo: 没有找到有效的 sudoers 资源,退出" 和 "sudo: 初始化审计插件 sudoers_audit 出错&q…...

讲解ThinkPHP的链式操作
数据库提供的链式操作方法,可以有效的提高数据存取的代码清晰度和开发效率,并且支持所有的CURD操作。 使用也比较简单,假如我们现在要查询一个User表的满足状态为1的前10条记录,并希望按照用户的创建时间排序 Db::table(think_u…...
Java技术栈 —— 微服务框架Spring Cloud —— Ruoyi-Cloud 学习(二)
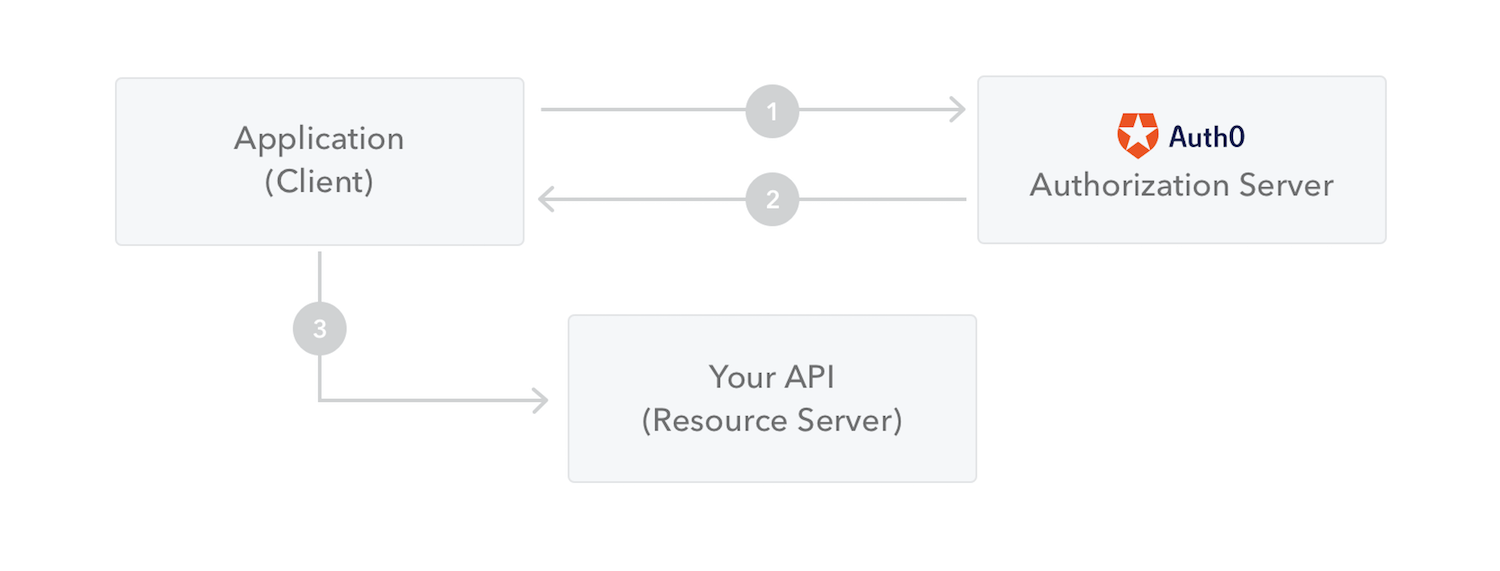
RuoYi项目开发过程 一、登录功能(鉴权模块)1.1 后端部分1.1.1 什么是JWT?1.1.2 什么是Base64?为什么需要它?1.1.3 SpringBoot注解解析1.1.4 依赖注入和控制反转1.1.5 什么是Restful?1.1.6 Log4j 2、Logpack、SLF4j日志框架1.1.7 如何将项目打包成指定bytecode字节…...
?)
如何进行软件测试和测试驱动开发(TDD)?
1. 软件测试概述 1.1 什么是软件测试? 软件测试是一种评估系统的过程,目的是发现潜在的错误或缺陷。通过对软件进行测试,开发者和测试人员可以确定软件是否符合预期的需求、功能是否正常运行,以及系统是否足够稳定和可靠。 1.2…...
linux 开机启动流程
1.打开电源 2.BIOS 有时间和启动方式 3.启动Systemd 其pid为1 4.挂载引导分区 /boot 5.启动各种服务 如rc.local...
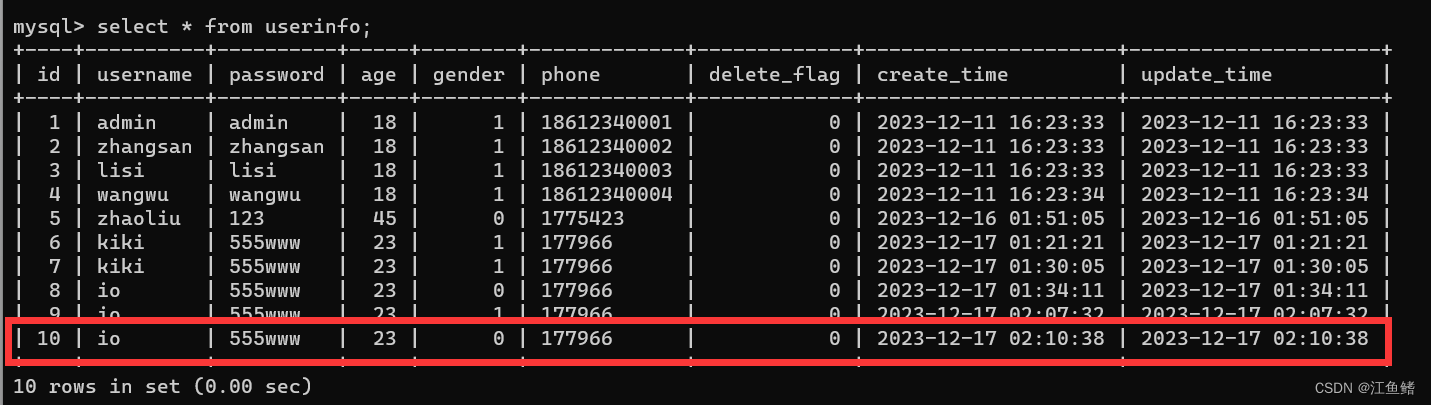
Mybatis 动态SQL的插入操作
需求 : 根据用户的输入情况进行插入 动态SQL:根据需求动态拼接SQL 用户往表中插入数据,有的数据可能不想插入,比如不想让别人知道自己的性别,性别就为空 insert into userinfo(username,password,age,gender,phone) values(?,?,?,?,?); insert into userinfo(username,…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
