elementui + vue2实现表格行的上下移动
场景:
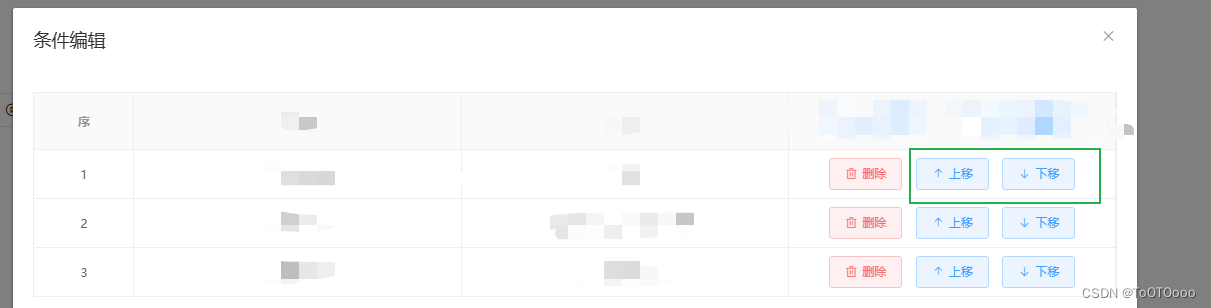
如上,要实现表格行的上下移动
实现:
<el-dialogappend-to-bodytitle="条件编辑":visible.sync="dialogVisible"width="60%"><el-table :data="data1" border style="width: 100%"><el-table-column type="index" label="序" width="100" align="center"></el-table-column><el-table-column prop="edit" label="" align="center"><template slot-scope="scope"><el-button:disabled="scope.$index === 0"plaintype="primary"icon="el-icon-top"@click="moveUp(scope.$index, scope.row)">上移</el-button><el-button:disabled="scope.$index === data1.length - 1"plaintype="primary"icon="el-icon-bottom"@click="moveDown(scope.$index, scope.row)">下移</el-button></template></el-table-column></el-table></el-dialog>
// 上移moveUp(index, row) {if(index !== 0){const currentRow = row;this.data1.splice(index, 1);this.data1.splice(index - 1, 0, currentRow);}},// 下移moveDown(index, row) {if(index !== this.data1.length-1){const currentRow = row;this.data1.splice(index, 1);this.data1.splice(index + 1, 0, currentRow);}},
参考:
点击上移或下移按钮对当前行进关联操作,如果是表格第一行则不能上移,如果是表格的最后一行,则不能进行下移,不能思意就是禁用。
当前需要获取到表格的index,可以通过:row-class-name="tableRowClassName"这个方法
---# 原因分析:
> 上移禁用功能可以根据row.index ===0 来判断,下移禁用根据row.index === tableDate.length - 1 来判断---# 解决方案:
>提示:这里填写该问题的具体解决方案:
关键性代码:// 上移功能moveUp(index) {const currentRow = this.tableData.splice(index, 1)[0]this.tableData.splice(index - 1, 0, currentRow)}// 下移功能moveDown(index) {const currentRow = this.tableData.splice(index, 1)[0]this.tableData.splice(index + 1, 0, currentRow)}原文
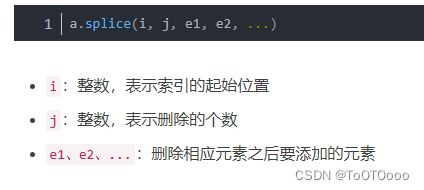
splice的使用
原文
相关文章:

elementui + vue2实现表格行的上下移动
场景: 如上,要实现表格行的上下移动 实现: <el-dialogappend-to-bodytitle"条件编辑":visible.sync"dialogVisible"width"60%"><el-table :data"data1" border style"width: 100%&q…...
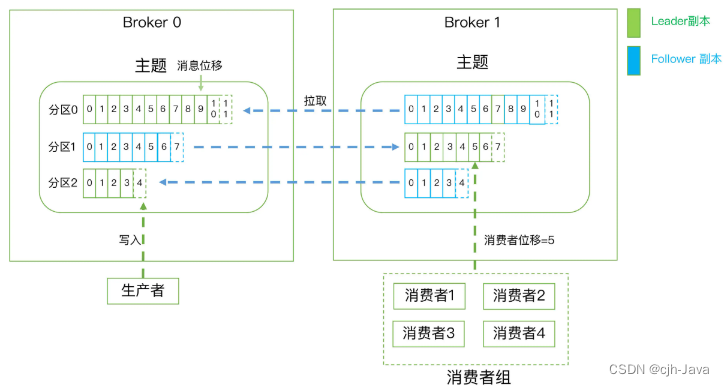
2、快速搞定Kafka术语
快速搞定Kafka术语 Kafka 服务端3层消息架构 Kafka 客户端Broker 如何持久化数据小结 Kafka 服务端 3层消息架构 第 1 层是主题层,每个主题可以配置 M 个分区,而每个分区又可以配置 N 个副本。第 2 层是分区层,每个分区的 N 个副本中只能有…...

CSS新手入门笔记整理:CSS3选择器
属性选择器 属性选择器,指的是通过“元素的属性”来选择元素的一种方式。 语法 元素[attr^"xxx"]{} 元素[attr$"xxx"]{} 元素[attr*"xxx"]{} 选择器 说明 E[attr^"xxx"] 选择元素E,其中E元素的attr属性是…...
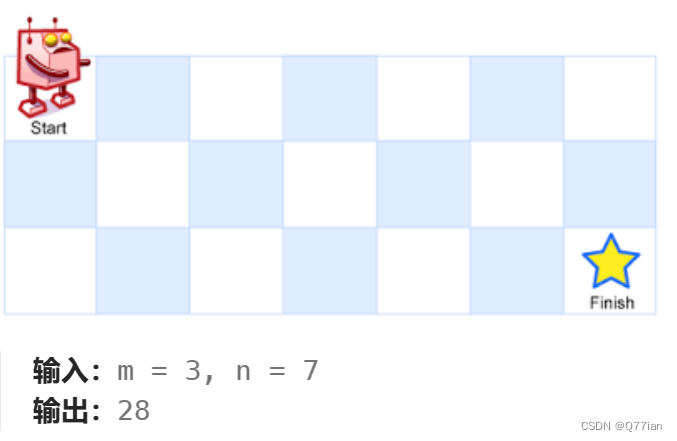
D34|不同路径
62.不同路径 初始思路: 1)确定dp数组以及下标的含义: dp[i][i]存放到第i1行和第i1列的方法数 2)确定递推公式: dp[i][i] dp[i -1][i] dp[i][i-1] 3)dp数组如何初始化 第0行是1; 第0列是1&a…...
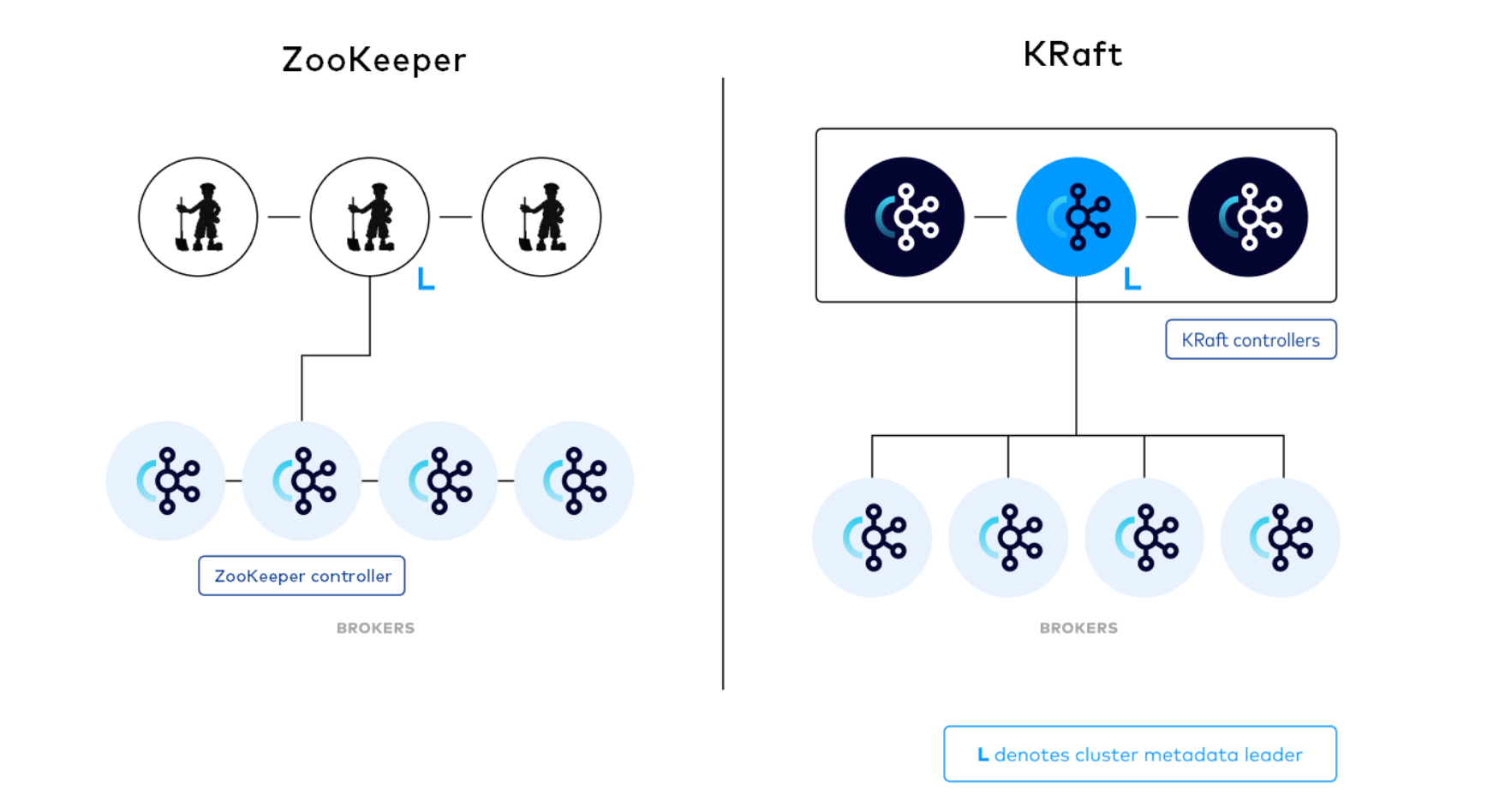
【运维】Kafka高可用: KRaft(不依赖zookeeper)集群搭建
文章目录 一. kafka kraft 集群介绍1. KRaft架构2. Controller 服务器3. Process Roles4. Quorum Voters5. kraft的工作原理 ing 二. 集群安装1. 安装1.1. 配置1.2. 格式化 2. 启动测试2.1. 启功节点服务2.2. 测试 本文主要介绍了 kafka raft集群架构: 与旧架构的不…...

Python 自动化之批量处理文件(一)
批量新建目录、文档Pro版本 文章目录 批量新建目录、文档Pro版本前言一、做成什么样子二、基本思路1.引入库2.基本架构 三、用户输入模块四、数据处理模块1.excel表格数据获取2.批量数据的生成 总结 前言 我来写一个不一样的批量新建吧。在工作中,有些同学应该会遇…...

力扣72. 编辑距离
动态规划 思路: 假设 dp[i][j] 是 word1 前 i 个字母到 word2 前 j 个字母的编辑距离;那么状态 dp[i][j] 状态的上一个状态有: dp[i - 1][j],word1 前 i - 1 个字母到 word2 前 j 个字母的编辑距离,此状态再插入一个字…...
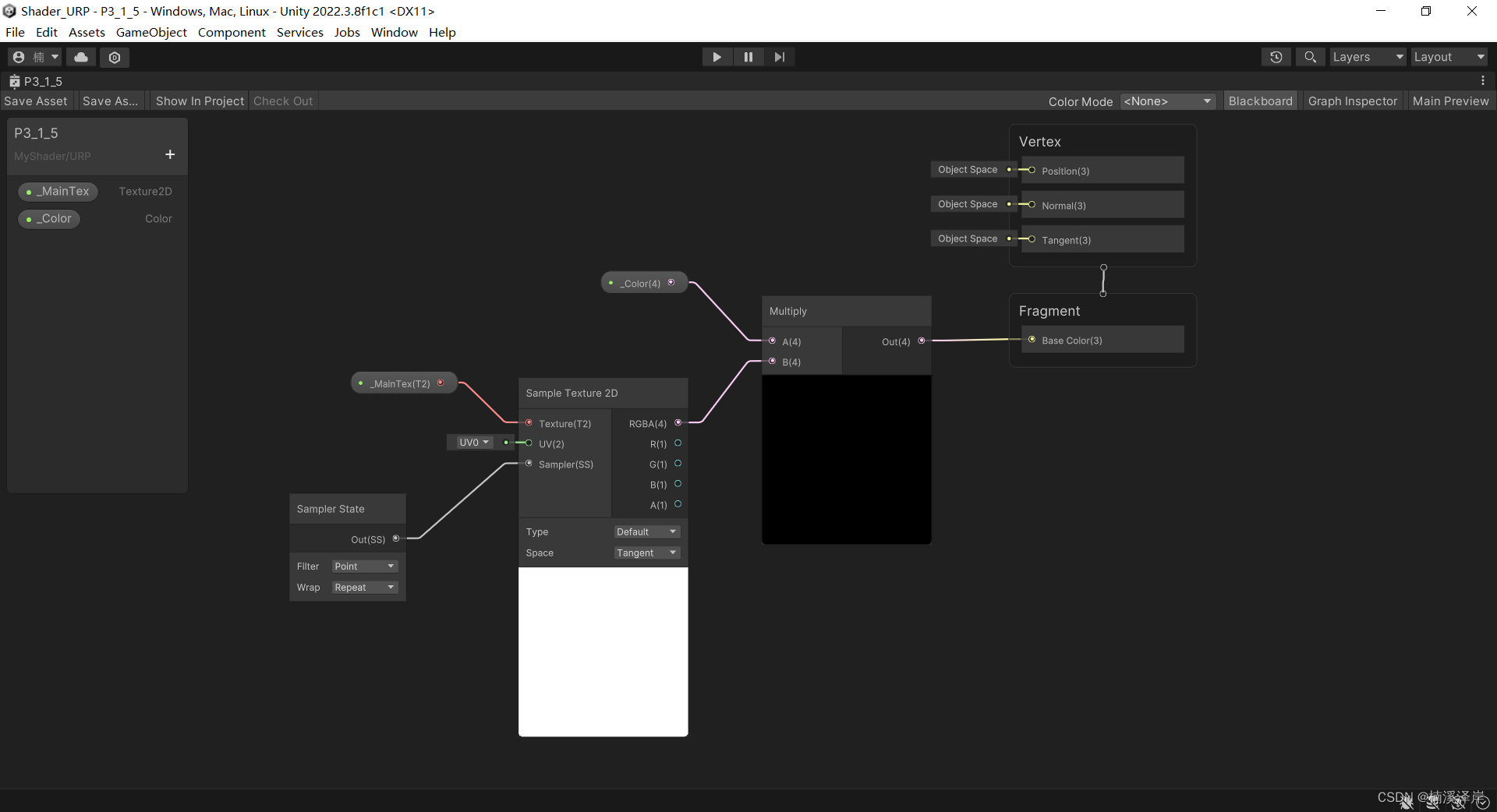
Unity中 URP Shader 的纹理与采样器的分离定义
文章目录 前言一、URP Shader 纹理采样的实现1、在属性面板定义一个2D变量用于接收纹理2、申明纹理3、申明采样器4、进行纹理采样 二、申明纹理 和 申明采样器内部干了什么1、申明纹理2、申明采样器 三、采样器设置采样器的传入格式1、纹理设置中,可以看见我们的采样…...

Electron学习第一天 ,启动项目
之前在安装官网的步骤操作,结果报错,找了好多办法,最后这种办法成功启动项目,并且没有报错,特此记录 特别提醒,最好安装淘宝镜像,npm 太慢,会导致报错问题,解决起来个人觉…...

WebService技术--随笔1
1.WebService 发展史 创建阶段(1990 年代末至 2000 年代初):在这个阶段,XML-RPC 和 SOAP 协议被引入,为跨平台和跨语言的应用程序集成提供了基础。XML-RPC 提供了一种基于 XML 的远程过程调用机制,而 SOAP…...

如何使用Docker将.Net6项目部署到Linux服务器(一)
目录 一 配置服务器环境 1.1 配置yum 1.1.1 更新yum包 1.1.2 yum命令 1.2 配置docker …...

第4章-第3节-Java中跟数组相关的几个算法以及综合应用
在写这篇博文之前,先大概说明一下,就是很常见的数组算法如求最大值、一维数组的遍历等,这里就不去专门说明了,只说一些有代表性的,然后就是冒泡排序算法很容易查阅到,这里也不专门说明了,只说明…...
AlexNet(pytorch)
AlexNet是2012年ISLVRC 2012(ImageNet Large Scale Visual Recognition Challenge)竞赛的冠军网络,分类准确率由传统的 70%提升到 80% 该网络的亮点在于: (1)首次利用 GPU 进行网络加速训练。 ÿ…...

【单调栈 】LeetCode321:拼接最大数
作者推荐 【动态规划】【广度优先搜索】LeetCode:2617 网格图中最少访问的格子数 本文涉及的知识点 单调栈 题目 给定长度分别为 m 和 n 的两个数组,其元素由 0-9 构成,表示两个自然数各位上的数字。现在从这两个数组中选出 k (k < m n) 个数字…...

TikTok与虚拟现实的完美交融:全新娱乐时代的开启
TikTok,这个风靡全球的短视频平台,与虚拟现实(VR)技术的深度结合,为用户呈现了一场全新的娱乐盛宴。虚拟现实技术为TikTok带来了更丰富、更沉浸的用户体验,标志着全新娱乐时代的开启。本文将深入探讨TikTok…...

PXI/PCIe/VPX机箱 ARM|x86 + FPGA测试测量板卡解决方案
PXI便携式测控系统是一种基于PXI总线的便携式测试测控系统,它填补了现有台式及机架式仪器在外场测控和便携测控应用上的空白,在军工国防、航空航天、兵器电子、船舶舰载等各个领域的外场测控场合和科学试验研究场合都有广泛的应用。由于PXI便携式测控系统…...

ES6 面试题 | 12.精选 ES6 面试题
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

【linux】Debian不能运行sudo的解决
一、问题: sudo: 没有找到有效的 sudoers 资源,退出 sudo: 初始化审计插件 sudoers_audit 出错 二、可用的方法: 出现 "sudo: 没有找到有效的 sudoers 资源,退出" 和 "sudo: 初始化审计插件 sudoers_audit 出错&q…...

讲解ThinkPHP的链式操作
数据库提供的链式操作方法,可以有效的提高数据存取的代码清晰度和开发效率,并且支持所有的CURD操作。 使用也比较简单,假如我们现在要查询一个User表的满足状态为1的前10条记录,并希望按照用户的创建时间排序 Db::table(think_u…...
Java技术栈 —— 微服务框架Spring Cloud —— Ruoyi-Cloud 学习(二)
RuoYi项目开发过程 一、登录功能(鉴权模块)1.1 后端部分1.1.1 什么是JWT?1.1.2 什么是Base64?为什么需要它?1.1.3 SpringBoot注解解析1.1.4 依赖注入和控制反转1.1.5 什么是Restful?1.1.6 Log4j 2、Logpack、SLF4j日志框架1.1.7 如何将项目打包成指定bytecode字节…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...
