C语言经典错误总结(三)
一.指针与数组理解
我们都知道定义一个数组然后对其进行各种想要的操作,但是你真的能够区分那些是对数组的操作,那些是通过指针实现的吗?
例如;arr[1]=10;这个是纯粹对数组操作实现的吗?
答案肯定不是,实际上我们定义一个数组之后只能做两件事:
1.确定数组的大小
2.获得一个指向该数组下标为0的元素指针
其他的操作本质上都是通过指针来实现的!
为什么我要将这个呢?因为如果你能够理解这个,那么你就会明确的知道下面这个结论:
任何一个数组下标运算都等同于一个对应的指针运算
讲到这里,我们有必要重新讲解下对数组名的理解:
int* fast=NULL, slow=NULL;但是你会发现在使用时,fast是指针,而slow却只是一个int型整数,原因就在于这里定义你写错了,正确的如下:
int* fast=NULL, *slow=NULL//注意slow前面加*指针常见错误二:
如果两个指针fast 和 slow不指向同一个数组中(同一个连续的空间),是不能够进行相减操作的
#include <stdio.h>
#include <string.h>
int main()
{char arr1 = "hello";char arr2 = "world";char* pc = malloc(strlen(arr1) + strlen(arr2));//操作//……//结束return 0;
}下面看我说的对不对:
1.用到malloc一定要检查空间大小,如果接下来我要进行strcat或者strcpy等操作,你确定开辟的空间够用吗?‘\0'我放在哪呢?所以,第一个问题就是malloc开辟空间不够大,我们应该开辟:
char* pc = malloc(strlen(arr1) + strlen(arr2)+1);2.一个动态开辟的内存,你确定一定开辟成功?所以我们开辟后一定要检查:
char* pc = malloc(strlen(arr1) + strlen(arr2)+1);
if (pc == NULL)
{return -1;
}3.指针有没有问题呢?你如果用完了指针,你是不是要归还给系统呢?
//结束
free(pc);
pc = NULL;因此,正确代码如下:
#include <stdio.h>
#include <string.h>
int main()
{char arr1 = "hello";char arr2 = "world";char* pc = malloc(strlen(arr1) + strlen(arr2)+1);if (pc == NULL){return -1;}//操作//……//结束free(pc);pc = NULL;return 0;
}int arr[3]={1,2,3};
int* p1=arr如果现在我们在:
int arr[3]={1,2,3};
int* p1=arr;
int* p2=p1;现在是不是p1和p2都指向数组首元素了,如果我再:
int arr[3]={1,2,3};
int* p1=arr;
int* p2=p1;
p2[1]=5;此时我想问p1[1]=?是不是也是5,没错,这就表明,新开辟p2指针是没有复制数据的,而是直接和p1指向同一块空间,明白这个有利于我们加深对指针底层理解!
二.边界计算和不对称边界
#include <stdio.h>
int main()
{int i = 0;int arr[] = { 1,2,3,4,5,6,7,8,9,10 };for (i; i <= 12; i++){arr[i] = 0;printf("hello world\n");}return 0;
}看这个代码,结果大家都知道,就是会陷入死循环,现在我为什么要提出这个简单问题呢?假如你写的i<=12改成i<=10,如果编译器检查不严格,也可能代码陷入死循环的状态,接下来我们就慢慢来告诉大家如何能够避免这种错误代码(即循环次数问题)。
现在假如我有100米长的围栏需要每10米立一根栏杆,请问我要买几根?
对于这个问题,大家肯定会不假思索的答出:11根
现在我们回到元素上,请问:16<=x<=37,满足条件的整数有多少?是20?21?还是22?
我想如果你对此不熟悉的话,可能需要一番思索,然后才会回答:22
现在我们有这样一个方法来快速的判断元素个数:
如果我们将16<=x<=37转换为;16<=x<38,这个你会发现:38-16=22,即为结果
这个对于编程有啥关系呢?你可能会问
首先这种不对称关系被称为:不对称边界,在数组中,该边界中的上界(大的边界)即为元素个数,这样可以非常简洁的表示而不会出错。
对比下面代码:
#include <stdio.h>
int main()
{int arr[10] = { 0 };for (int i = 0; i <= 9; i++){arr[i] = i;}return 0;
}#include <stdio.h>
int main()
{int arr[10] = { 0 };for (int i = 0; i <10; i++){arr[i] = i;}return 0;
}将i<=9改成i<10,这样看起来可能不美观,但是可以非常有效帮助到你,如果你对此还感兴趣,可以去了解缓冲区知识,那里运用不对称边界又是美妙的体会。
相关文章:
)
C语言经典错误总结(三)
一.指针与数组理解 我们都知道定义一个数组然后对其进行各种想要的操作,但是你真的能够区分那些是对数组的操作,那些是通过指针实现的吗? 例如;arr[1]10;这个是纯粹对数组操作实现的吗? 答案肯定不是,实际上我们定义…...

Ubuntu系统入门指南:基础操作和使用
Ubuntu系统的基础操作和使用 一、引言二、安装Ubuntu系统三、Ubuntu系统的基础操作3.1、界面介绍3.2、应用程序的安装和卸载3.3、文件管理3.4、系统设置 四、Ubuntu系统的日常使用4.1、使用软件中心4.2、浏览器的使用和网络连接设置4.3、邮件客户端的配置和使用4.4、文件备份和…...
MyBatis原理解读
我们项目中多用MyBatis进行数据库的读写,开源的MyBatis-Plus框架对其进行了增强,使用上更加简单,我们之前的很多项目也是直接用的MyBatis-Plus。 数据库操作的时候,简单的单表读写,我们可以直接在方法里链式组装SQL,复杂的SQL或涉及多表联合join的,需要在xml手写SQL语句…...
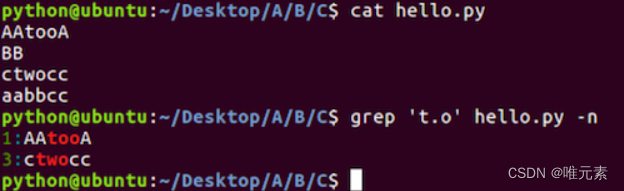
Linux---文本搜索命令
1. grep命令的使用 命令说明grep文本搜索 grep命令效果图: 2. grep命令选项的使用 命令选项说明-i忽略大小写-n显示匹配行号-v显示不包含匹配文本的所有行 -i命令选项效果图: -n命令选项效果图: -v命令选项效果图: 3. grep命令结合正则表达式的使用 正则表达式说明^以指…...

Unity中Shader语义的理解
前言 以下内容主要是个人理解,如有错误,欢迎严厉批评指正。 一、语义的形式在Shader中是必要的吗? 不是必要的。 使用HLSL和CG语言来编写Shader需要语义,使用GLSL编写Shader不需要。 二、语义的意义? 语义是什么&…...

Flink系列之:Top-N
Flink系列之:Top-N 一、TOP-N二、无排名输出优化 一、TOP-N 适用于流、批Top-N 查询可以根据指定列排序后获得前 N 个最小或最大值。最小值和最大值集都被认为是Top-N查询。在需要从批表或流表中仅显示 N 个底部或 N 个顶部记录时,Top-N 查询是非常有用…...
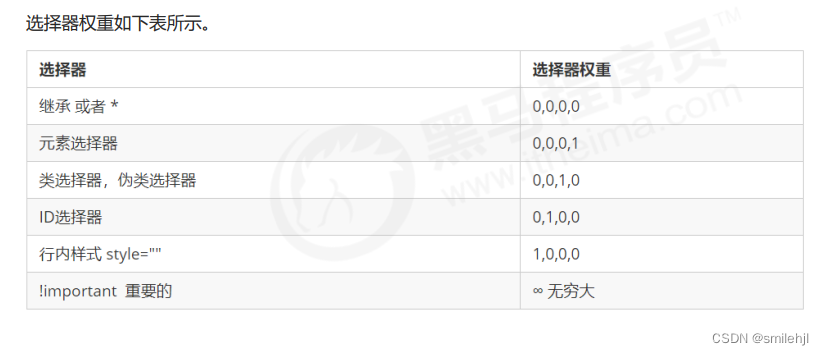
CSS的三大特性(层叠性、继承性、优先级---------很重要)
CSS 有三个非常重要的三个特性:层叠性、继承性、优先级。 层叠性 场景:相同选择器给设置相同的样式,此时一个样式就会覆盖(层叠)另一个冲突的样式。层叠性主要解决样式冲突 的问题 原则: 样式冲突&am…...
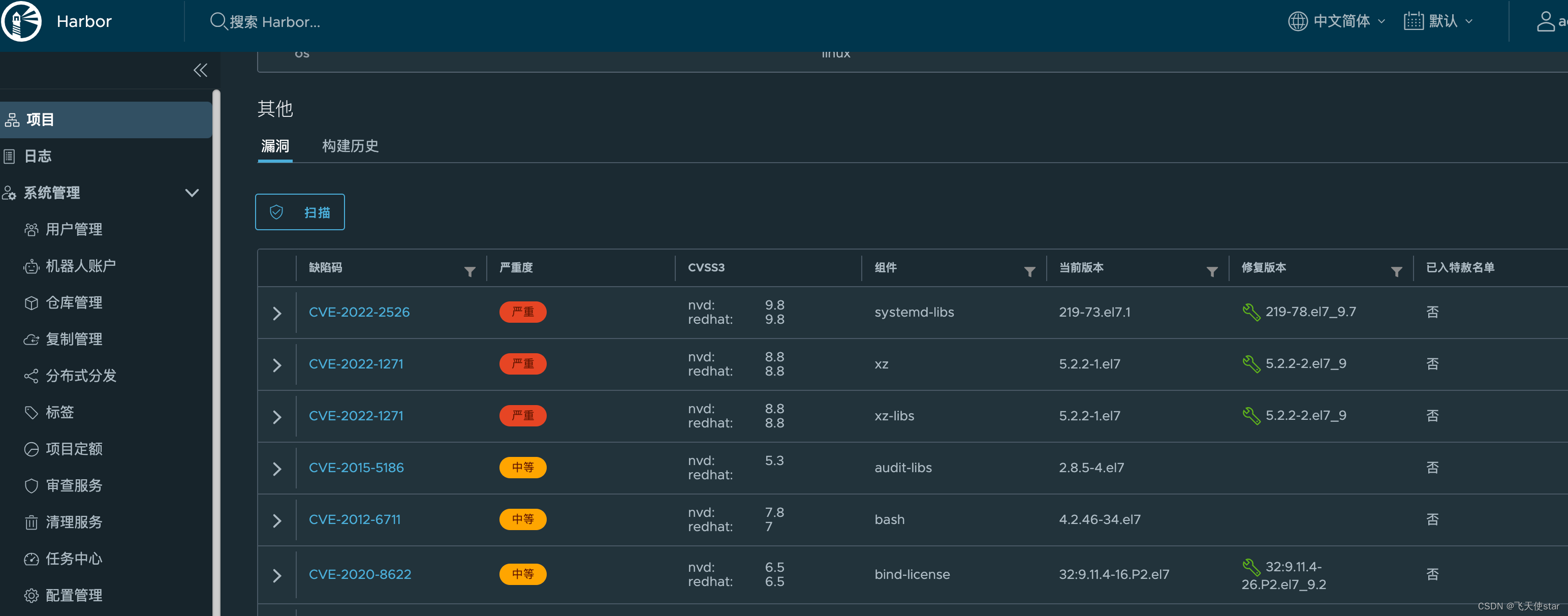
飞天使-docker知识点10-docker总结
文章目录 docker 知识点汇总docker chatgpt解释学习路线cmd和 ENTRYPOINT 的区别harbor安装漏洞扫描 docker 知识点汇总 docker 基础用法 docker 镜像基础用法 docker 容器网络 docker 存储卷 dockerfile docker仓库 harbor docker-compose docker chatgpt解释学习路线 学习…...

旅游管理虚拟情景实训教学系统演示
首先,虚拟情景实训教学系统为旅游管理专业的学生提供了一个全新的实践平台。在传统的旅游管理教学中,学生往往只能通过理论学习来了解相关知识,而无法亲身实践。虚拟情景实训教学系统则可以通过模拟真实的旅游场景,让学生能够亲身…...

Linux Shell——输入输出命令详解
Shell 输入输出 1. read2. echo3. printf 总结 最近学习了shell相关语法,顺便总结一下关于shell的输入输出命令read和echo、printf。 1. read shell的输入命令,可以从标准控制台中读取一行,并把输入行中的每个字段赋值给指定的变量 可以看到…...
MFC 第一个窗口程序
目录 一、新建Windows桌面应用程序,空项目 二、修改项目属性 三、编写程序 一、新建Windows桌面应用程序,空项目 创建MFCBase.cpp,整个项目很干净 二、修改项目属性 使用多字节编码 使用MFC库 三、编写程序 需要包含 afxwin.h 文件&…...

SQL语句的执行顺序怎么理解?
SQL语句的执行顺序怎么理解? 我们常常会被SQL其书写顺序和执行顺序之间的差异所迷惑。理解这两者的区别,对于编写高效、可靠的SQL代码至关重要。今天,让我们用一些生动的例子和场景来深入探讨SQL的执行顺序。 一、书写顺序 VS 执行顺序 SQ…...

js解析.shp文件
效果图 原理与源码 本文采用的是shapefile.js工具 这里是他的npm地址 https://www.npmjs.com/package/shapefile 这是他的unpkg地址,可以点开查看源码 https://unpkg.com/shapefile0.6.6/dist/shapefile.js 这个最关键的核心问题是如何用这个工具,网上…...

关于“Python”的核心知识点整理大全25
目录 10.3.4 else 代码块、 10.3.5 处理 FileNotFoundError 异常 alice.py 在这个示例中,try代码块引发FileNotFoundError异常,因此Python找出与该错误匹配的 except代码块,并运行其中的代码。最终的结果是显示一条友好的错误消息&#x…...
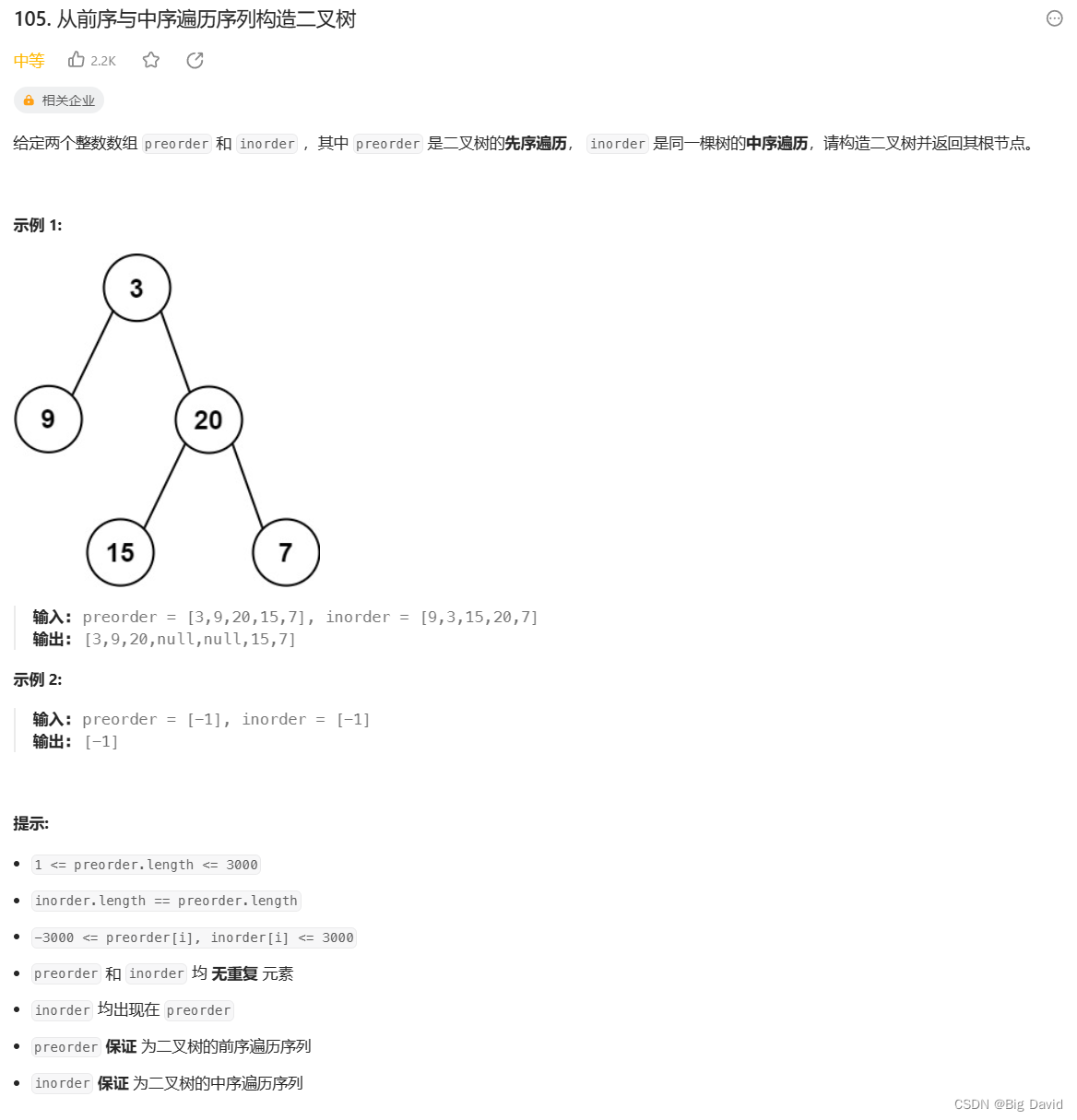
代码随想录刷题题Day15
刷题的第十五天,希望自己能够不断坚持下去,迎来蜕变。😀😀😀 刷题语言:C Day15 任务 ● 513.找树左下角的值 ● 112. 路径总和 113.路径总和ii ● 106.从中序与后序遍历序列构造二叉树 105.从前序与中序遍历…...
软件设计师——信息安全(一)
📑前言 本文主要是【信息安全】——软件设计师——信息安全的文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是听风与他🥇 ☁️博客首页:CSDN主页听风与他 🌄…...

git必须掌握:git远程变动怎么解决
如何已经指定了选择分支 那下面的分支名称可以省略 如果远程分支存在变动,通常 git 推送的流程如下: 首先,使用 git fetch 命令从远程仓库获取最新的分支信息和变动。 git fetch然后,可以使用 git merge 或者 git rebase 命令进…...

Python里的时间模块
time 模块 时间表示方式 时间戳 timestamp:表示的是从 1970 年1月1日 00:00:00 开始按秒计算的偏移量UTC(Coordinated Universal Time, 世界协调时)亦即格林威治天文时间,世界标准时间。在中国为 UTC+8 DST(Daylight Saving Time) 即夏令时;结构化时间(struct_time): …...
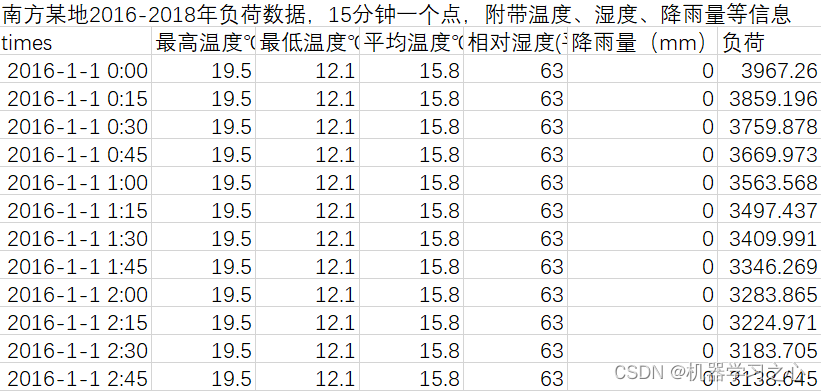
SCI一区级 | Matlab实现GWO-CNN-GRU-selfAttention多变量多步时间序列预测
SCI一区级 | Matlab实现GWO-CNN-GRU-selfAttention多变量多步时间序列预测 目录 SCI一区级 | Matlab实现GWO-CNN-GRU-selfAttention多变量多步时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.Matlab实现GWO-CNN-GRU-selfAttention灰狼算法优化卷积门控循环…...

C#学习相关系列之自定义遍历器
在C#中,自定义遍历器需要实现IEnumerable接口和IEnumerator接口。其中,IEnumerable接口包含一个GetEnumerator方法,该方法返回一个IEnumerator接口的实例,而IEnumerator接口包含Current、MoveNext和Reset方法。 IEnumerable&#…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
