光栅化渲染:可见性问题和深度缓冲区算法
在前面第二章中,我们了解到,在投影点(屏幕空间中的点)的第三个坐标中,我们存储原始顶点 z 坐标(相机空间中点的 z 坐标):

当一个像素与多个三角形重叠时,查找三角形表面上一点的 z 坐标非常有用。 我们找到 z 坐标的方法是使用我们在上一章中学到的重心坐标对原始顶点 z 坐标进行插值。 换句话说,我们可以将三角形顶点的 z 坐标视为任何其他顶点属性,并以与上一章中插值颜色相同的方式对它们进行插值。 在详细研究如何计算 z 坐标之前,让我们先解释一下为什么需要这样做。
NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎
1、深度缓冲或 Z 缓冲算法和隐藏面剔除
当一个像素与一个点重叠时,我们通过该像素看到的是三角形表面上的一小块区域,为了简化,我们将其简化为单个点(在图 1 中表示为 P):

图1:当一个像素与一个三角形重叠时,这个像素对应于三角形表面上的一个点(图中记为P)
因此,覆盖三角形的每个像素对应于该三角形表面上的一个点。 当然,如果一个像素覆盖多个三角形,那么我们就有几个这样的点。 发生这种情况时的问题是找到这些点中哪一个是可见的。 我们在图 2 中以 2D 形式说明了这个概念:
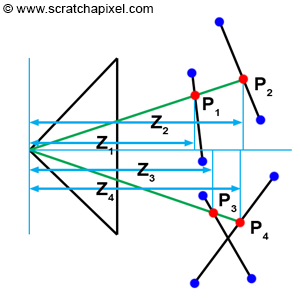
图 2:当一个像素与多个三角形重叠时,我们可以使用三角形 z 坐标上的点来找到这些三角形中哪一个距离相机最近
我们可以从后到前测试三角形(此技术需要首先通过减小深度对三角形进行排序),但当三角形彼此相交时,这并不总是有效(图 2,底部)。 唯一可靠的解决方案是计算像素重叠的每个三角形的深度,然后比较这些深度值以找出哪一个最接近相机。
如果查看图 2,你可以看到图像中的一个像素与 P1 和 P2 中的两个三角形重叠。 然而,P1 z 坐标 (Z1) 低于 P2 z 坐标 (Z2),因此我们可以推断 P1 在 P2 之前。 请注意,需要此技术,因为三角形是按“随机”顺序测试的。 正如之前提到的,我们可以按深度递减的顺序对三角形进行排序,但这还不够好。 一般来说,它们只是按照程序中指定的顺序进行测试,因此可以先测试离相机较近的三角形T1,然后再测试较远的三角形T2。 如果我们不比较这些三角形的深度,那么在这种情况下我们最终会看到最后测试的三角形 (T2),而实际上我们应该看到 T1。 正如之前多次提到的,这称为可见性(visibility)问题或隐藏面(hidden surface)问题。 对对象进行排序以便正确绘制对象的算法称为可见表面算法或隐藏面去除算法。 我们接下来要研究的深度缓冲区(depth buffer)或z缓冲区(z-buffer)算法就属于此类算法。
可见性问题的一种解决方案是使用深度缓冲区或 z 缓冲区。 深度缓冲区只不过是一个二维浮点数组,其尺寸与帧缓冲区相同,用于在三角形被光栅化时存储对象的深度。 创建此数组时,我们用一个非常大的数字初始化数组中的每个像素。 如果我们发现某个像素与当前三角形重叠,我们会执行以下操作:
- 我们首先计算像素重叠的三角形上的点的 z 坐标或深度。
- 然后,我们将当前三角形深度与该像素的深度缓冲区中存储的值进行比较。
- 如果我们发现深度缓冲区中存储的值大于三角形上点的深度,则新点比深度缓冲区中该像素位置处存储的点更靠近观察者或相机。 然后,深度缓冲区中存储的值将替换为新的深度,并且帧缓冲区将更新为当前的三角形颜色。 另一方面,如果深度缓冲区中存储的值小于当前深度样本,则像素重叠的三角形将被深度缓冲区中当前存储的深度的对象隐藏。
请注意,一旦处理完所有三角形,深度缓冲区就会包含“某种”图像,它表示场景中对象的可见部分与相机之间的“距离”(这不是距离,而是 z- 通过相机可见的每个点的坐标)。 深度缓冲区本质上对于解决可见性问题很有用,但是,它也可以在后处理中用于执行诸如 2D 景深、添加雾等操作。所有这些效果在 3D 中效果更好,但在 2D 通常更快,但结果并不总是像 3D 那样准确。
以下是深度缓冲区算法的伪代码实现:
float *depthBuffer = new float [imageWidth * imageHeight];
// Initialize depth-buffer with a very large number
for (uint32_t y = 0; y < imageHeight; ++y)for (uint32_t x = 0; x < imageWidth; ++x)depthBuffer[y][x] = INFINITY;for (each triangle in the scene) {// Project triangle vertices...// Compute 2D triangle bounding-box...for (uint32_t y = bbox.min.y; y <= bbox.max.y; ++y) {for (uint32_t x = bbox.min.x; x <= bbox.max.x; ++x) {if (pixelOverlapsTriangle(i + 0.5, j + 0.5) {// Compute the z-coordinate of the point on the triangle surfacefloat z = computeDepth(...);// Current point is closest than object stored in depth/frame-bufferif (z < depthBuffer[y][x]) {// Update depth-buffer with that depthdepthBuffer[y][x] = z;frameBuffer[y][x] = triangleColor;}}} }
}2、通过插值求 Z

图 3:我们可以通过使用重心坐标对三角形顶点 z 坐标进行插值来找到 P 的深度吗?
希望深度缓冲区的原理简单易懂。 我们现在需要做的就是解释如何计算深度值。 首先,让我们再次重复一下深度值是什么。 当一个像素与一个三角形重叠时,它会与三角形表面上的一个小表面重叠,正如引言中提到的,我们将其简化为一个点(图1中的点P)。 我们在这里要找到的是该点的 z 坐标。 正如本章前面提到的,如果我们知道三角形顶点的 z 坐标(我们这样做,它们存储在投影点的 z 坐标中),我们需要做的就是使用 P 的重心坐标对这些坐标进行插值(图 4):

图 4:通过线性插值求出点的 y 坐标
计算公式如下:

从技术上讲,这听起来很合理,但不幸的是,它不起作用。 让我们看看为什么。 问题不在于公式本身,它完全没问题。 问题是,一旦三角形的顶点被投影到画布上(一旦我们执行了透视分割),那么 z(我们想要插值的值)就不再在 2D 三角形的表面上线性变化。 通过 2D 示例更容易演示这一点。
秘密就在图 4 中。想象一下,我们想要找到 2D 空间中由两个顶点 V0 和 V1 定义的一条线的“图像”。 画布由水平绿线表示。 这条线距坐标系原点 1 个单位(沿 z 轴)。 如果我们从 V0 和 V1 追踪直线到原点,那么我们就会在两个点处与绿线相交(在图中表示为 V0' 和 V1')。 该点的 z 坐标为 1,因为它们位于画布上,距原点 1 个单位。 使用透视投影可以轻松计算点的 x 坐标。 我们只需要将原始顶点的 x 坐标除以 z 坐标即可。 我们得到:
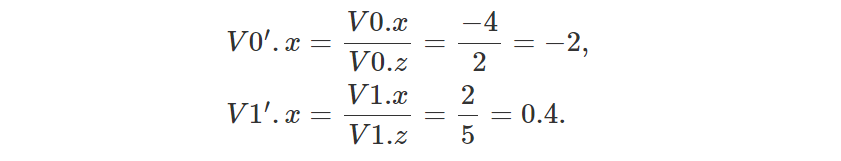
练习的目标是找到 P 的 z 坐标,P 是由 V0 和 V1 定义的直线上的一个点。 在这个例子中,我们对 P 的了解就是它在绿线上的投影 P' 的位置。 P'的坐标是{0,1}。 该问题类似于尝试查找像素重叠的三角形上的点的 z 坐标。 在我们的示例中,P' 是像素,P 是像素重叠的三角形上的点。 我们现在需要做的是计算 P' 相对于 V0' 和 V1' 的“重心坐标”。 我们将结果值称为 λ 。 与我们的三角形重心坐标一样,λ 也在 [0,1] 范围内。 要找到 λ ,我们只需获取 V0' 和 P' 之间的距离(沿 x 轴),然后将该数字除以 V0' 和 V1' 之间的距离。 如果使用 λ 对原始顶点 V0 和 V1 的 z 坐标进行线性插值来求出 P 的深度,那么我们应该得到数字 4(通过看图我们很容易看出 P 的坐标为 {0 ,4})。 我们首先计算 λ :

如果我们现在对 V0 和 V1 z 坐标进行线性插值来找到 P z 坐标,我们会得到:

这不是我们期望的值! 在本例中使用 P 的“重心坐标”或 λ 对原始顶点 z 坐标进行插值来查找 P z 坐标是行不通的。 为什么? 原因很简单。 透视投影保留线条但不保留距离。 从图 4 中很容易看出,V0 和 P 之间的距离与 V0 和 V1 之间的距离的比率 (0.666) 与 V0' 和 P' 之间的距离与 V0 之间的距离的比率不同。 ' 和 V1' (0.833)。 如果 λ 等于 0.666 就可以正常工作,但问题是,它等于 0.833! 那么,我们如何求出P的z坐标呢?
该问题的解决方案是通过使用 λ 对顶点 V0 和 V1 z 坐标的倒数进行插值来计算 P的z 坐标的倒数。 换句话说,解决方案是:

让我们检查一下它是否有效:

如果现在取这个结果的倒数,我们就得到 P的z 坐标的值 4。这是正确的结果! 如前所述,解决方案是使用重心坐标对顶点的 z 坐标进行线性插值,然后反转结果数以找到 P 的深度(其 z 坐标)。 对于我们的三角形,公式是:


图 5:透视投影保留线条,但不保留距离
现在让我们更正式地研究这个问题。 为什么我们需要对顶点的逆 z 坐标进行插值? 正式的解释有点复杂,如果你愿意的话可以跳过。
让我们考虑相机空间中由两个顶点定义的线,其坐标分别表示为 (X0,Z0) 和 (X1,Z1)。 这些顶点在屏幕上的投影分别表示为 S0 和 S1(在我们的示例中,我们假设相机原点和画布之间的距离为 1,如图 5 所示)。 我们将 S 称为 S0 和 S1 定义的直线上的点。 S 在 2D 线上有一个对应的点 P,其坐标为 (X,Z = 1)(在本例中我们假设投影点的屏幕或垂直线距坐标系原点 1 个单位)。 最后,参数 t 和 q 的定义如下:

我们也可以写成:

因此,可以通过插值计算点 P 的 (X,Z) 坐标(等式 1):
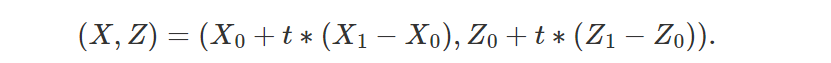
类似地(等式 2):

S 是一个一维点(它已投影在屏幕上),因此它没有 z 坐标。 S 也可以计算为:

因此:

如果我们将分子替换为方程 1,将分母替换为方程 2,则我们得到(方程 3):

我们也得到:
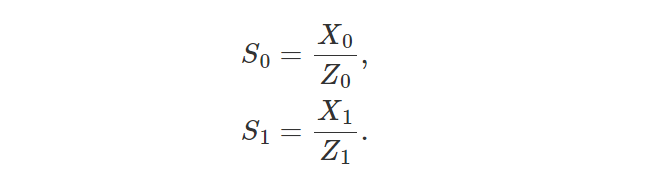
因此(等式 4):

如果现在将方程 3 中的 X0 和 X1 替换为方程 4,我们得到(等式5):

记住等式 1(等式 6):

如果结合方程 5 和 6,我们得到:
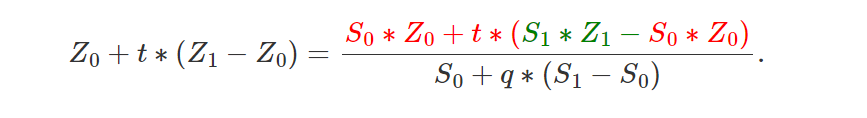
可以简化为:

我们现在可以用 q 来表达参数 t:

如果代入等式 6 中的 t,我们得到:

因此可以得到:
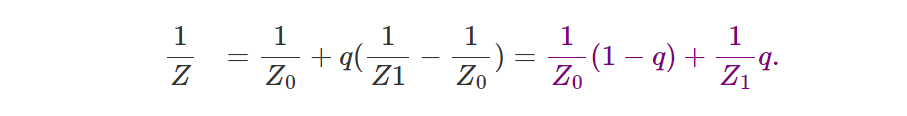
这就是我们最终想要得到的公式。
3、其他可见表面算法
正如简介中提到的,z 缓冲区算法属于隐藏表面去除或可见表面算法系列。 这些算法可以分为两类:对象空间算法和图像空间算法。 本课我们没有讨论的“painter”算法属于前者,而z-buffer算法则属于后者。 painter算法背后的概念大致是从后到前绘制或绘制对象。 该技术需要对对象进行深度排序。 正如本章前面所解释的,第一个对象以任意顺序传递到渲染器,然后当两个三角形彼此相交时,很难弄清楚哪个三角形在另一个前面(从而决定应该绘制哪个三角形) 第一的)。 该算法已不再使用,但 z 缓冲区非常常见(GPU 使用它)。
原文链接:可见性和深度缓冲区算法 - BimAnt
相关文章:
光栅化渲染:可见性问题和深度缓冲区算法
在前面第二章中,我们了解到,在投影点(屏幕空间中的点)的第三个坐标中,我们存储原始顶点 z 坐标(相机空间中点的 z 坐标): 当一个像素与多个三角形重叠时,查找三角形表面上…...
docker入门小结
docker是什么?它有什么优势? 快速获取开箱即用的程序 docker使得所有的应用传输就像我们日常通过聊天工具文件传输一样,发送方将程序传输到超级码头而接收方也只需通过超级码头进行获取即可,就像一只鲸鱼拖着货物来回运输一样。…...
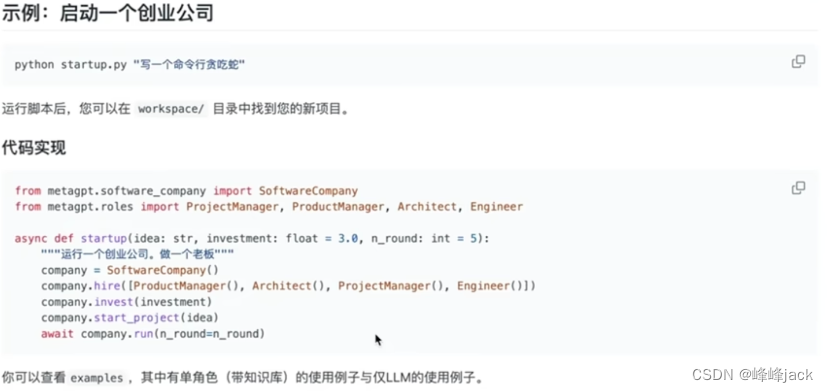
LLM Agent发展演进历史(观看metagpt视频笔记)
LLM相关的6篇重要的论文,其中4篇来自谷歌,2篇来自openai。技术路径演进大致是:SSL (Self-Supervised Learning) -> SFT (Supervised FineTune) IT (Instruction Tuning) -> RLHF。 word embedding的问题:新词如何处理&…...
面经——part2)
Linux(操作系统)面经——part2
1、请你说说进程和线程的区别 1.进程是操作系统资源分配和调度的最小单位,实现操作系统内部的并发;线程是进程的子任务,cpu可以识别、执行的最小单位,实现程序内部的并发。 2.一个进程最少有一个线程或有多个,一个线程…...

Flink系列之:WITH clause
Flink系列之:WITH clause 适用流、批提供了一种编写辅助语句以在较大查询中使用的方法。这些语句通常称为公共表表达式 (CTE),可以被视为定义仅针对一个查询而存在的临时视图。 WITH 语句的语法为: WITH <with_item_definition> [ , …...
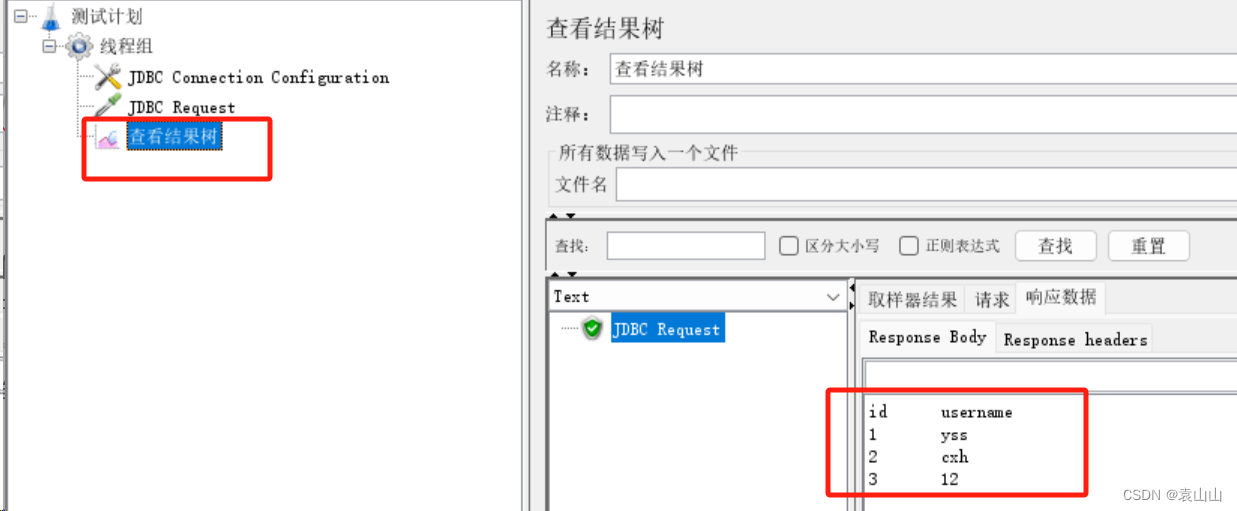
JMeter直连数据库
JMeter直连数据库 使用场景操作步骤 使用场景 用作请求的参数化 登录时需要的用户名,密码可以从数据库中查询获取 用作结果的断言 添加购物车下订单,检查接口返回的订单号,是否与数据库中生成的订单号一致 清理垃圾数据 添加商品后ÿ…...
Linux部署MySQL5.7和8.0版本 | CentOS和Ubuntu系统详细步骤安装
一、MySQL数据库管理系统安装部署【简单】 简介 MySQL数据库管理系统(后续简称MySQL),是一款知名的数据库系统,其特点是:轻量、简单、功能丰富。 MySQL数据库可谓是软件行业的明星产品,无论是后端开发、…...
)
STL中set和multiset容器的用法(轻松易懂~)
目录 1. 基本概念 2. 构造和赋值 3. 大小和交换 4. 插入 和 删除 5. 统计 和 查找 6. set容器的排序 1. 基本概念 set和multiset属于关联式容器,底层结构式二叉树,所有元素都会在插入时自动排序。 如果你对容器的概念,或是二叉树不太了…...
Codeforces Round 915 (Div. 2)
Constructive Problems(Problem - A - Codeforces) 题目大意:现在有一片城市被摧毁了,需要进行重建,当一个城市水平相邻和竖直相邻的位置都至少有一个城市的时候,该城市可以被重建。所有城市排成n行m列的矩…...
)
C语言经典错误总结(三)
一.指针与数组理解 我们都知道定义一个数组然后对其进行各种想要的操作,但是你真的能够区分那些是对数组的操作,那些是通过指针实现的吗? 例如;arr[1]10;这个是纯粹对数组操作实现的吗? 答案肯定不是,实际上我们定义…...

Ubuntu系统入门指南:基础操作和使用
Ubuntu系统的基础操作和使用 一、引言二、安装Ubuntu系统三、Ubuntu系统的基础操作3.1、界面介绍3.2、应用程序的安装和卸载3.3、文件管理3.4、系统设置 四、Ubuntu系统的日常使用4.1、使用软件中心4.2、浏览器的使用和网络连接设置4.3、邮件客户端的配置和使用4.4、文件备份和…...
MyBatis原理解读
我们项目中多用MyBatis进行数据库的读写,开源的MyBatis-Plus框架对其进行了增强,使用上更加简单,我们之前的很多项目也是直接用的MyBatis-Plus。 数据库操作的时候,简单的单表读写,我们可以直接在方法里链式组装SQL,复杂的SQL或涉及多表联合join的,需要在xml手写SQL语句…...
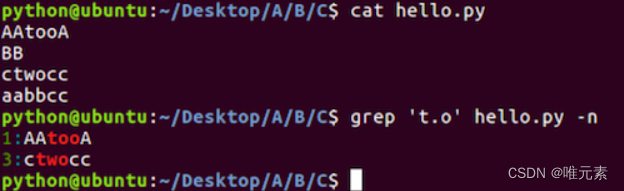
Linux---文本搜索命令
1. grep命令的使用 命令说明grep文本搜索 grep命令效果图: 2. grep命令选项的使用 命令选项说明-i忽略大小写-n显示匹配行号-v显示不包含匹配文本的所有行 -i命令选项效果图: -n命令选项效果图: -v命令选项效果图: 3. grep命令结合正则表达式的使用 正则表达式说明^以指…...

Unity中Shader语义的理解
前言 以下内容主要是个人理解,如有错误,欢迎严厉批评指正。 一、语义的形式在Shader中是必要的吗? 不是必要的。 使用HLSL和CG语言来编写Shader需要语义,使用GLSL编写Shader不需要。 二、语义的意义? 语义是什么&…...

Flink系列之:Top-N
Flink系列之:Top-N 一、TOP-N二、无排名输出优化 一、TOP-N 适用于流、批Top-N 查询可以根据指定列排序后获得前 N 个最小或最大值。最小值和最大值集都被认为是Top-N查询。在需要从批表或流表中仅显示 N 个底部或 N 个顶部记录时,Top-N 查询是非常有用…...
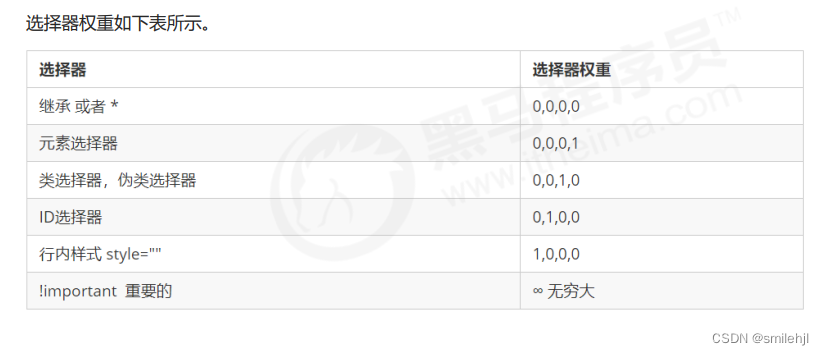
CSS的三大特性(层叠性、继承性、优先级---------很重要)
CSS 有三个非常重要的三个特性:层叠性、继承性、优先级。 层叠性 场景:相同选择器给设置相同的样式,此时一个样式就会覆盖(层叠)另一个冲突的样式。层叠性主要解决样式冲突 的问题 原则: 样式冲突&am…...
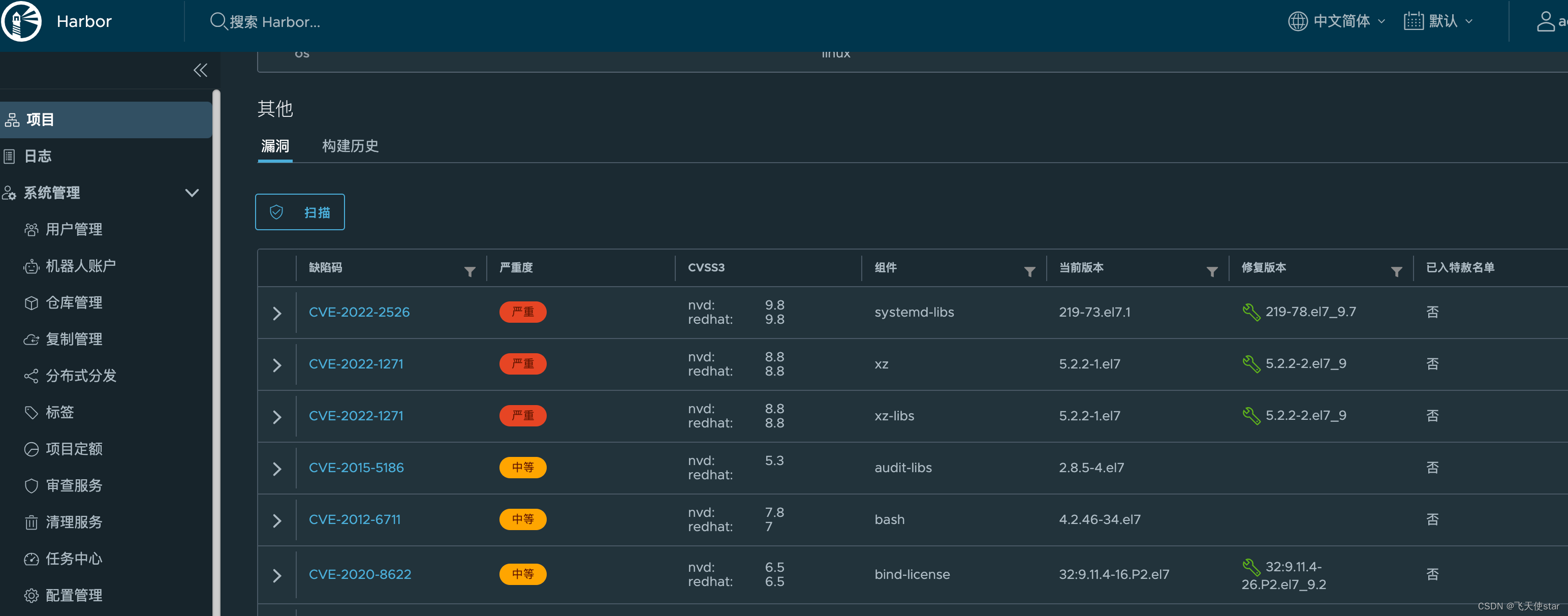
飞天使-docker知识点10-docker总结
文章目录 docker 知识点汇总docker chatgpt解释学习路线cmd和 ENTRYPOINT 的区别harbor安装漏洞扫描 docker 知识点汇总 docker 基础用法 docker 镜像基础用法 docker 容器网络 docker 存储卷 dockerfile docker仓库 harbor docker-compose docker chatgpt解释学习路线 学习…...

旅游管理虚拟情景实训教学系统演示
首先,虚拟情景实训教学系统为旅游管理专业的学生提供了一个全新的实践平台。在传统的旅游管理教学中,学生往往只能通过理论学习来了解相关知识,而无法亲身实践。虚拟情景实训教学系统则可以通过模拟真实的旅游场景,让学生能够亲身…...

Linux Shell——输入输出命令详解
Shell 输入输出 1. read2. echo3. printf 总结 最近学习了shell相关语法,顺便总结一下关于shell的输入输出命令read和echo、printf。 1. read shell的输入命令,可以从标准控制台中读取一行,并把输入行中的每个字段赋值给指定的变量 可以看到…...
MFC 第一个窗口程序
目录 一、新建Windows桌面应用程序,空项目 二、修改项目属性 三、编写程序 一、新建Windows桌面应用程序,空项目 创建MFCBase.cpp,整个项目很干净 二、修改项目属性 使用多字节编码 使用MFC库 三、编写程序 需要包含 afxwin.h 文件&…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...
