会旋转的树,你见过吗?
🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨
🐻强烈推荐优质专栏: 🍔🍟🌯C++的世界(持续更新中)
🐻推荐专栏1: 🍔🍟🌯C语言初阶
🐻推荐专栏2: 🍔🍟🌯C语言进阶
🔑个人信条: 🌵知行合一
🍉本篇简介:>:AVL树的实现,旋转的详细分析,抽象图,具体图分步骤讲解,保姆级教学。
金句分享:
✨人生若只如初见,✨
✨何事秋风悲画扇。✨
前言
前面我们学习了二叉搜索树,二叉搜索树如果左右子树高度相差不大,那么效率还是可观的,比如:满二叉搜索树的查询效率为 O(logn).
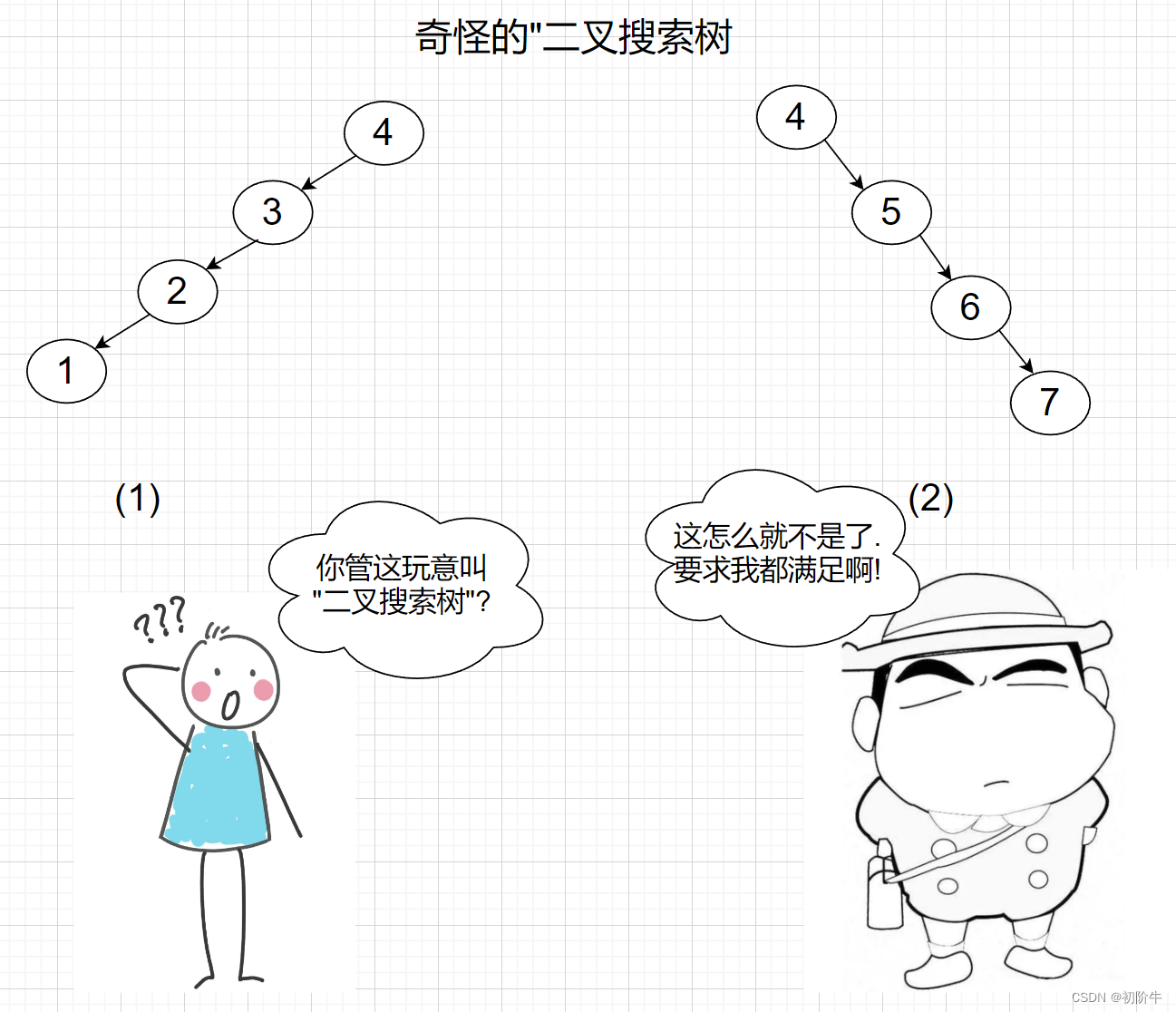
但是,如果插入的数据是有序的,或者大部分有序,则会导致 “二叉搜索树” 退化为类似于链表的结构.
那链表查询数据的时间复杂度牛牛就不用多说了吧.答案: O(n)
示例:
目录
- 前言
- 一、AVL树的介绍
- 二、AVL树的模拟实现
- 🍭结点类
- 🍔AVL树的框架:
- 2.1 "插入"操作(重点)
- ①:右旋
- (1) 右旋具体图:
- (2)右旋抽象图:
- ②左旋:
- (1)左旋具体图:
- (2)左旋抽象图
- ③右左双旋
- (1)右左双旋具体图
- (2)右左双旋抽象图
- ④左右双旋
- (1)左右双旋具体图
- (2)左右双旋抽象图
- "插入"操作的代码实现:
- 2.2 中序遍历:
- 2.3 AVL树的"高度"
- 2.4 验证AVL树
- 结语
一、AVL树的介绍
AVL树是一种自"平衡二叉搜索树",它的每个节点存储一个关键字,具有以下特点:
-
每个节点的左右子树高度差至多为1,也就是说,
AVL树的任何一个节点的左右子树高度差不超过1。 -
对于任意一个节点,其左子树和右子树都是一个
AVL树。 -
AVL树中的每个节点都能保证左子树中的所有节点小于当前节点的关键字,右子树中的所有节点大于当前节点的关键字。(也就是满足二叉搜索树的性质)
如果我们定义 平衡因子=右子树的高度-左子树的高度
则树中每个结点的平衡因子的绝对值 不超过1 即可以为( 1 0 -1三种)
1:表示右子树比左子树高.
0:表示左子树和右子树一样高.
-1:表示左子树比右子树高.
每当向AVL树中插入、删除节点时,AVL树会自动地进行旋转操作将树变为平衡状态,从而保证了AVL树的平衡性。
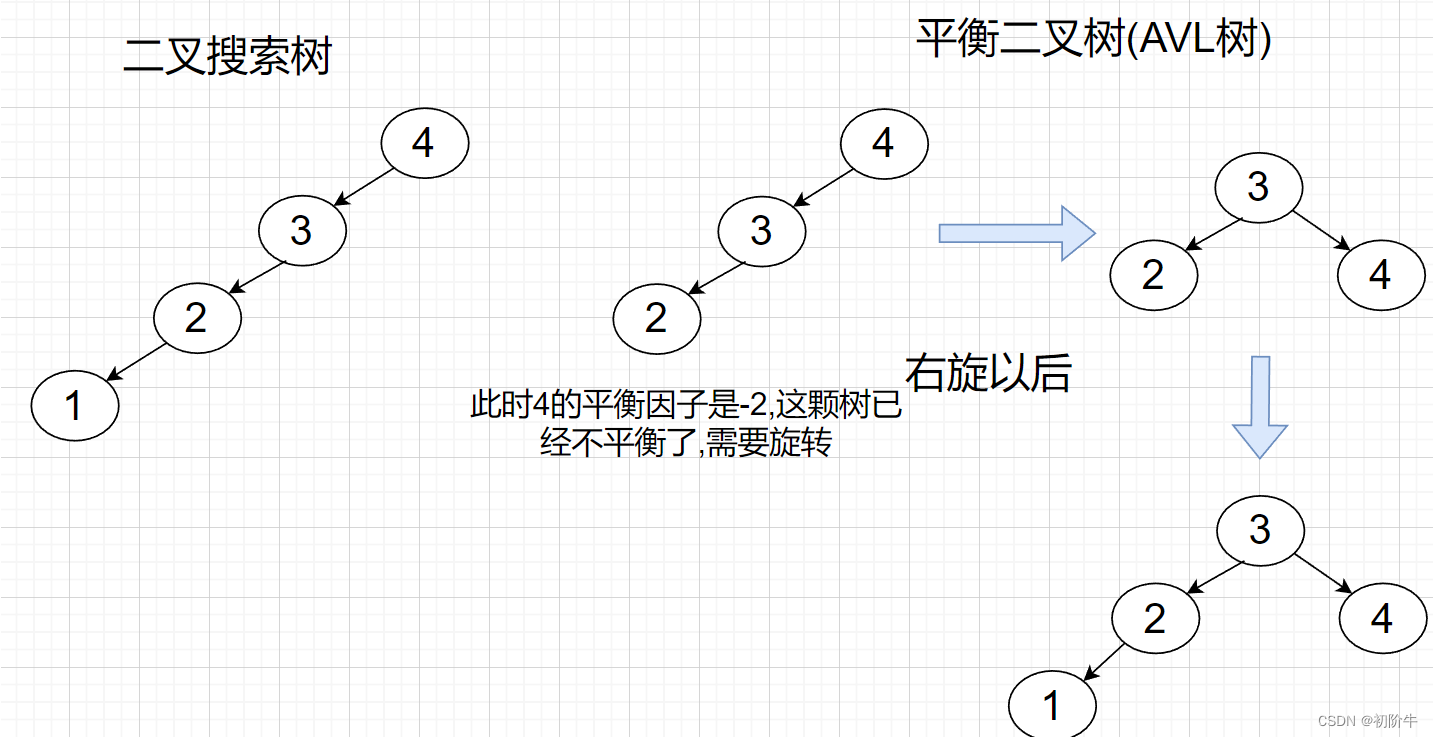
会旋转的树才够强,AVL树的查询数据的时间复杂度总是控制在 O(logn)量级.
二、AVL树的模拟实现
补充知识点:
在c++中 pair类是一个模板类,用于将两个值组成一个单元,也就是我们称为的键值对.
template<class T1, class T2>
struct pair {typedef T1 first_type;typedef T2 second_type;T1 first; // 第一个元素T2 second; // 第二个元素// 默认构造函数pair() : first(T1()), second(T2()) {}// 初始化构造函数pair(const T1& x, const T2& y) : first(x), second(y) {}
};
🍭结点类
没错,AVL树是三叉树,为了方便旋转,我们需要多存储一个指针域(_parent) ,指向父节点.
template<class K, class V>
struct AVLTreeNode
{pair<K, V> _kv; //键值对AVLTreeNode<K, V>* _left; //左子树AVLTreeNode<K, V>* _right; //右子树AVLTreeNode<K, V>* _parent; //父节点int _bf; // balance factor平衡因子//构造AVLTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}
};
🍔AVL树的框架:
// AVL树的结构
template<class K,class V>
class AVLTree
{typedef AVLTreeNode<K,V> Node;
public:AVLTree(): _root(nullptr){}// 在AVL树中插入值为data的节点bool Insert(const pair<K, V>& kv);void InOrder();// AVL树的验证bool IsAVLTree(){return _IsAVLTree(_root);}private:// 根据AVL树的概念验证proot是否为有效的AVL树bool _IsAVLTree(Node* root);size_t _Height(Node* root);void _InOrder(Node* root);// 右单旋void RotateR(Node* parent);// 左单旋void RotateL(Node* parent);// 右左双旋void RotateRL(Node* parent);// 左右双旋void RotateLR(Node* parent);private:Node* _root;
};2.1 "插入"操作(重点)
注意: 本篇实现的AVL树,平衡因子是右子树高度—左子树高度.
故:
当新增结点在父亲结点的左边时,左子树的高度+1,则平衡因子-1.
当新增结点在父亲结点的右边时,右子树的高度+1,则平衡因子+1.
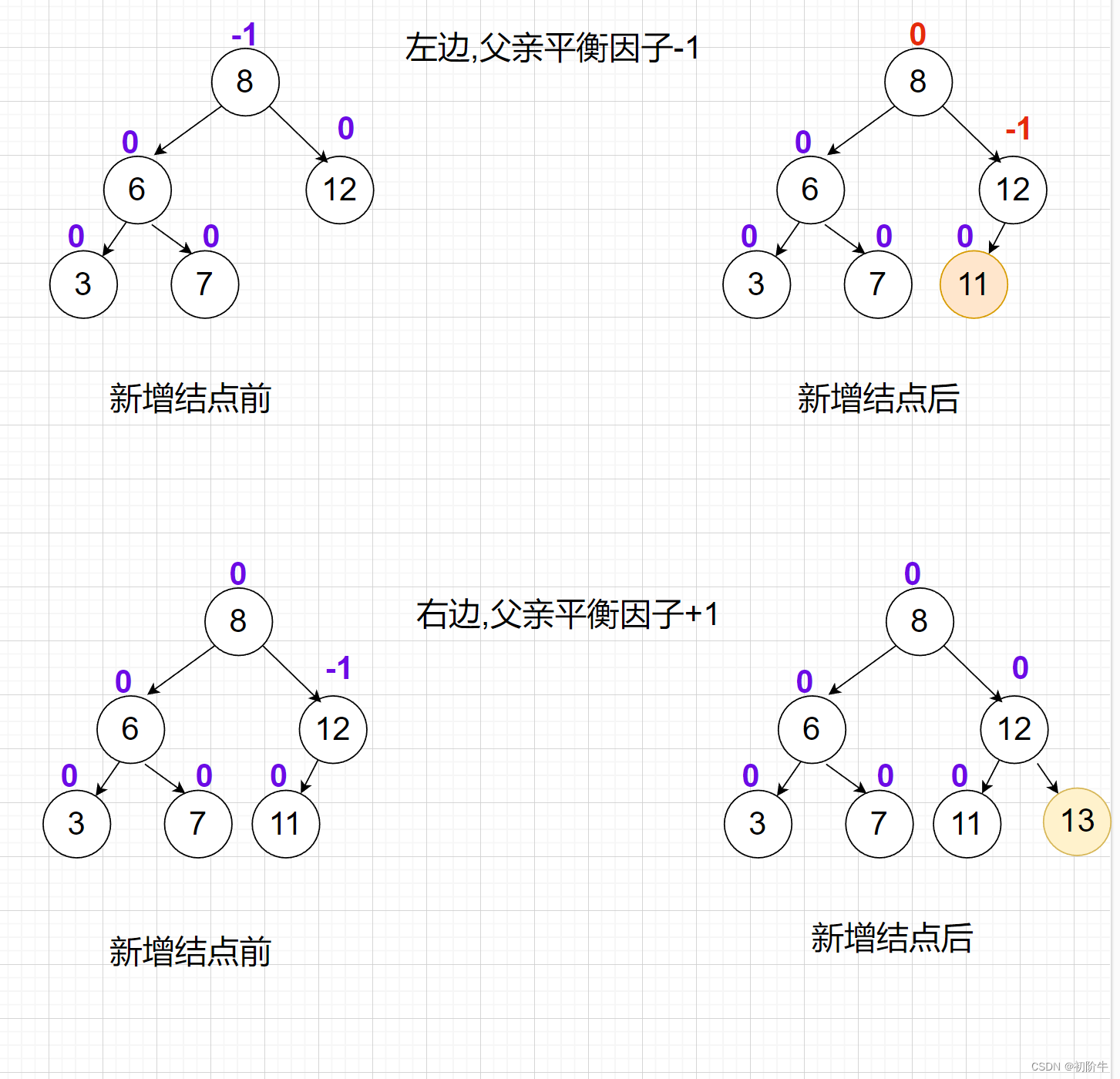
子树的平衡因子变化,可能会影响祖先路径上的结点,需要继续向上更新.
(1) 当新增结点后,父节点的平衡因子变成0,则插入结束.
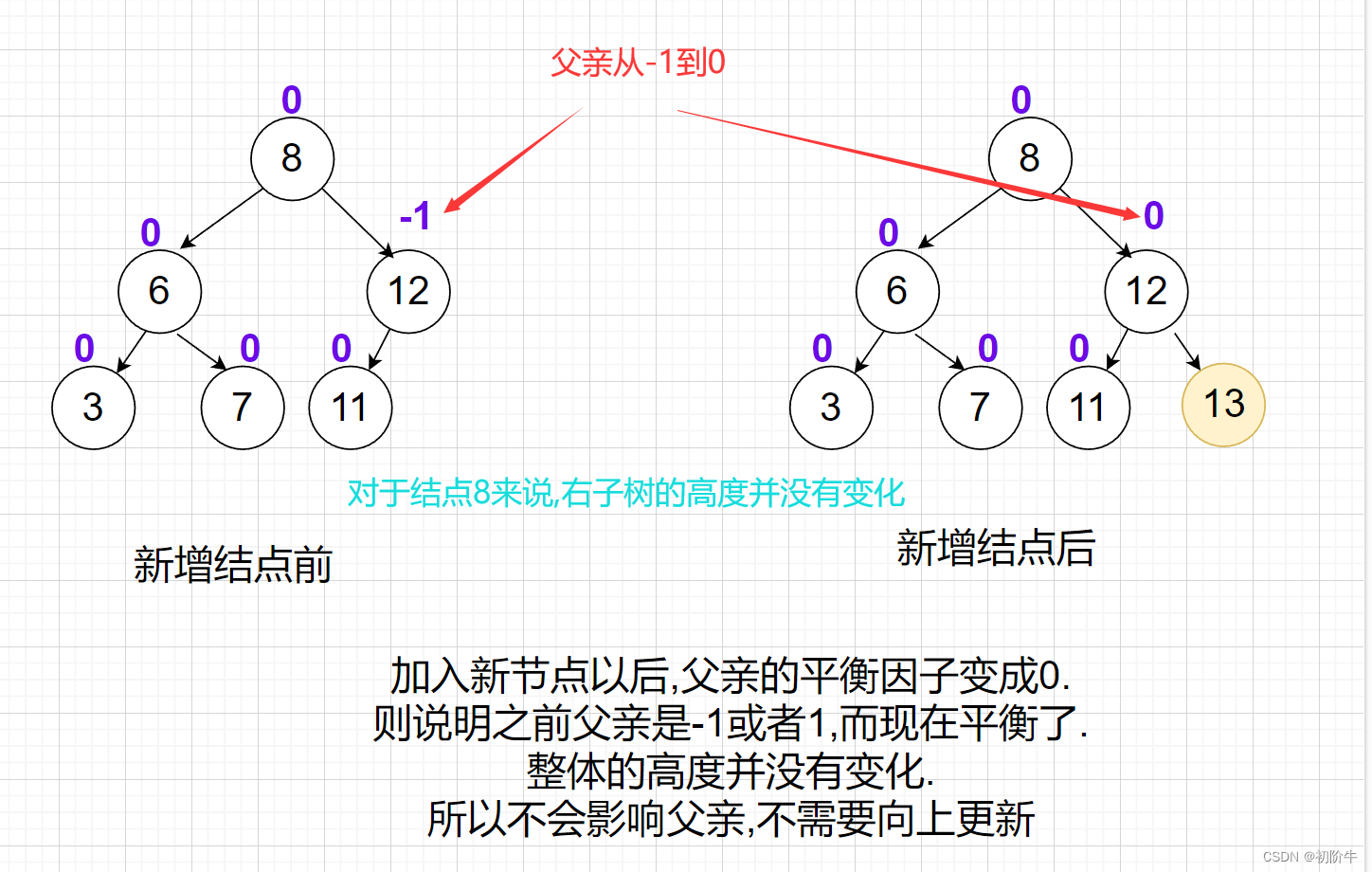
(2) 当新增结点后,父节点的平衡因子变成1或者-1,则需要向上更新.
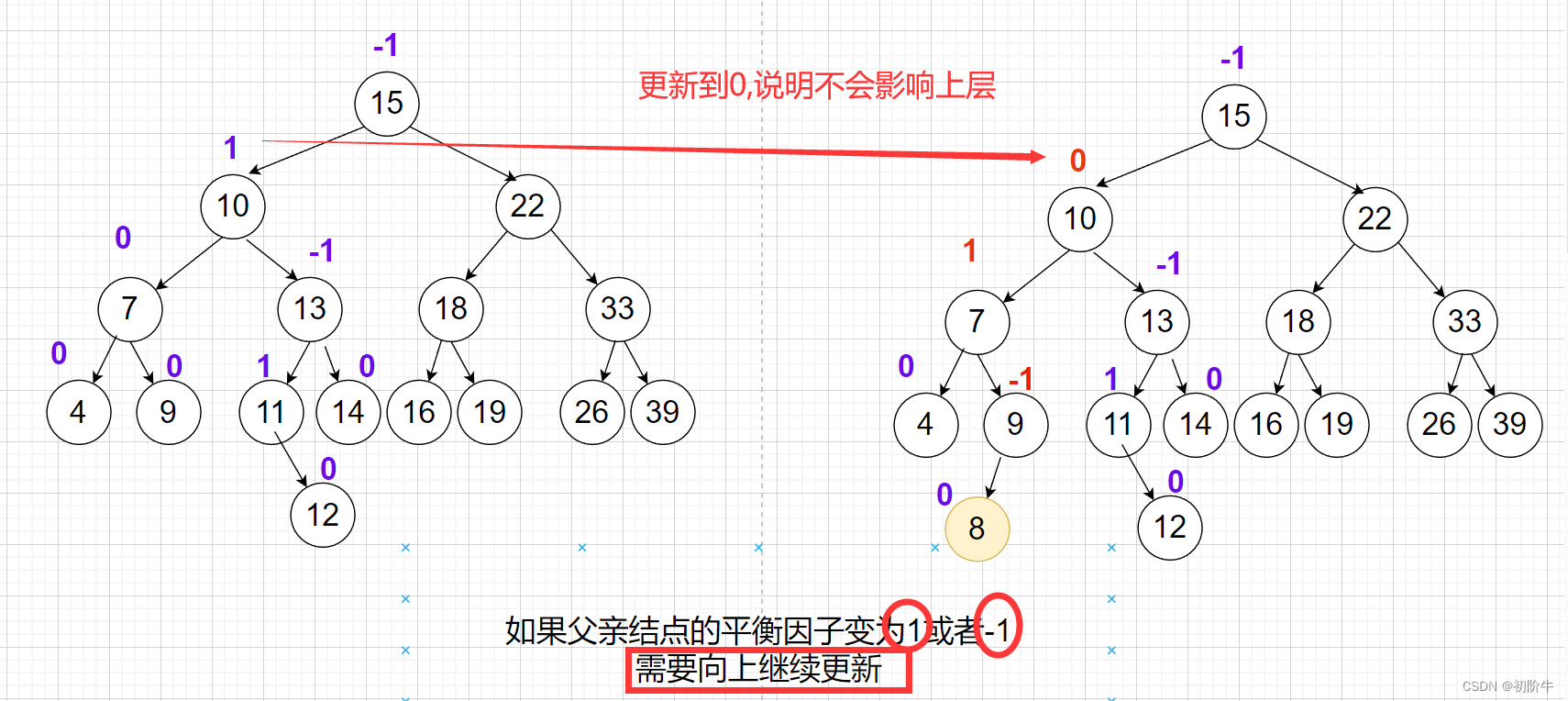
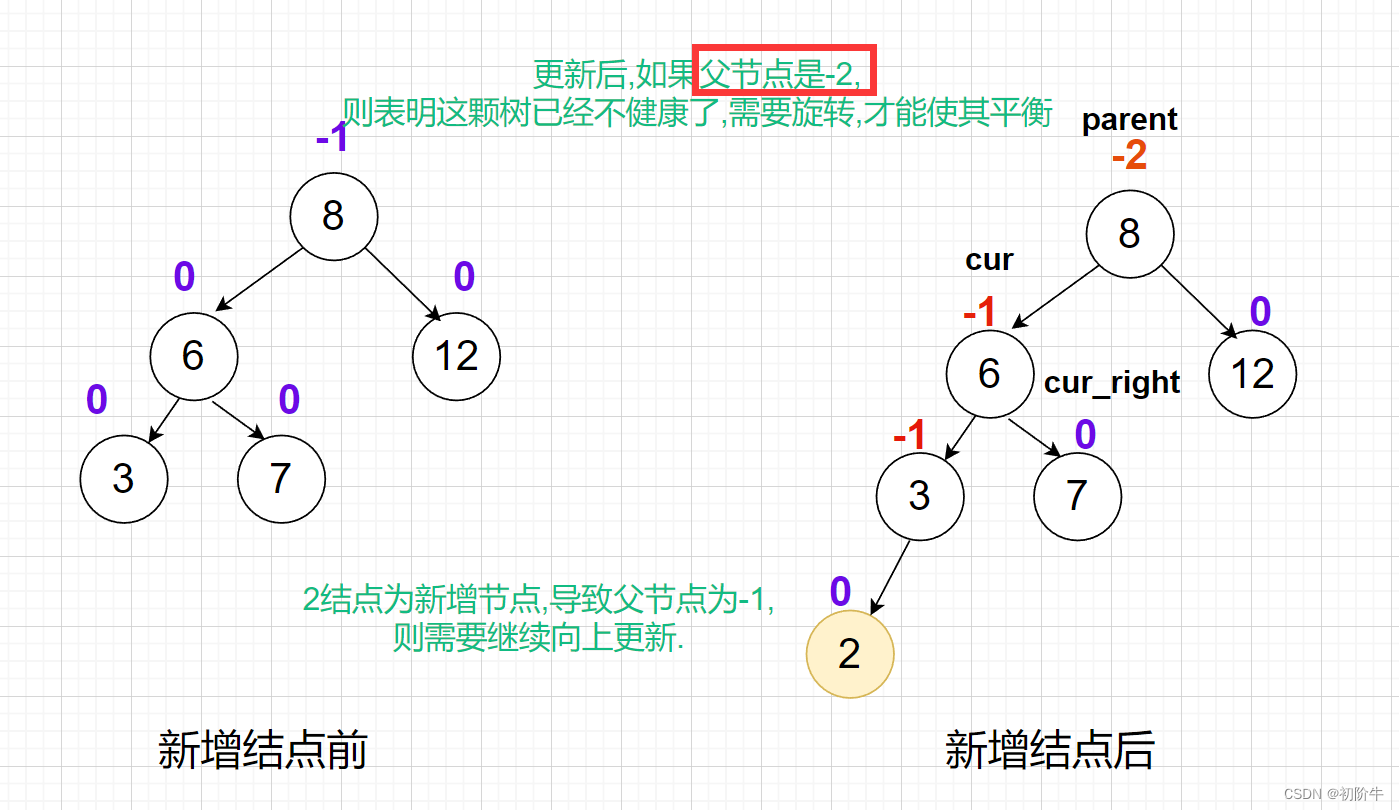
(3)当新增结点后,父节点的平衡因子变成2或者-2需要旋转.
①:右旋
当继续向上更新到父节点是平衡因子-2时,则需要右旋.
因为左边比右边高,需要旋转到右边.使其平衡.
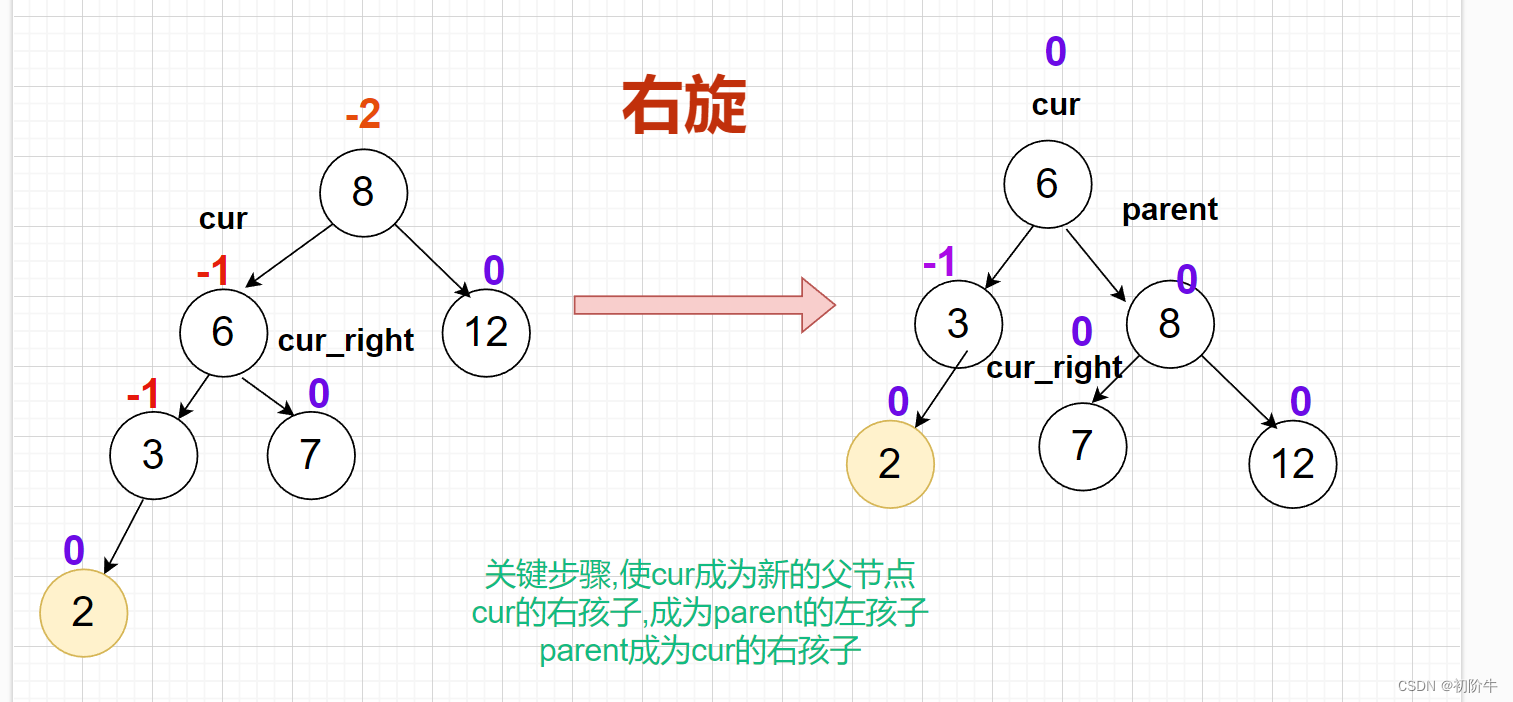
(1) 右旋具体图:
关键步骤:
使
cur成为新的父节点
cur的右孩子,成为parent的左孩子
parent成为cur的右孩子
(2)右旋抽象图:
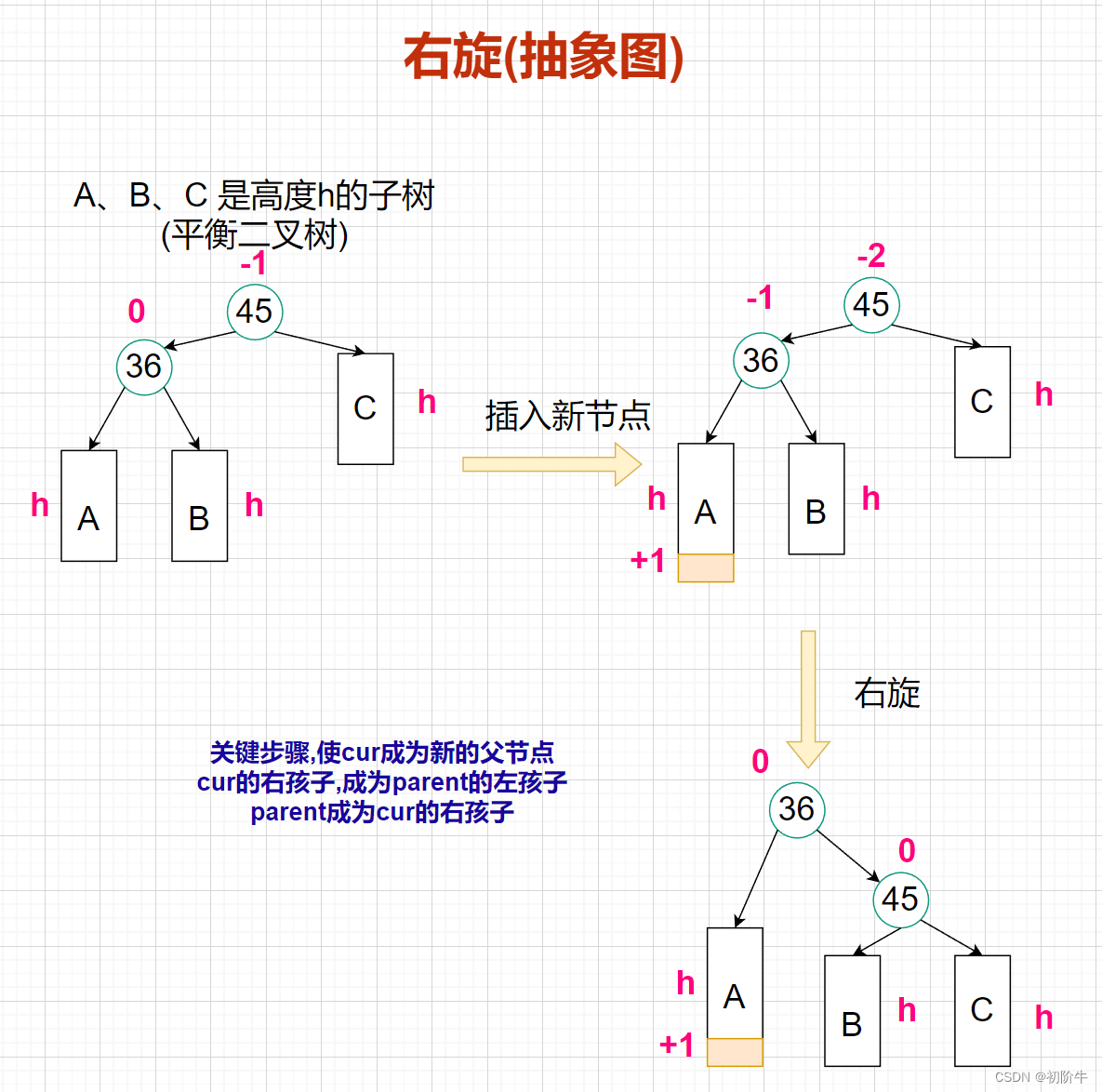
更新平衡因子:
从抽象图可以看出,右旋旋转后,平衡因子cur parent都可以无脑设置为0.
代码实现:
//右旋
template<class K,class V>
void AVLTree<K,V>::RotateR(Node* parent)
{Node* ppnode = parent->_parent;Node* cur = parent->_left;Node* cur_right = cur->_right;//cur的右子树变成parent的左子树if (cur_right) { //cur_right 可能不存在parent->_left = cur_right;cur_right->_parent = parent;//保持三叉连}else {parent->_left = nullptr;}//parent变成cur的右子树cur->_right = parent; parent->_parent = cur;//保持三叉连if (ppnode) { cur->_parent = ppnode;if (ppnode->_left == parent) { //如果是上面的左子树ppnode->_left = cur;}else {ppnode->_right = cur; //如果是上面的右子树}}else { //如果ppnode是nullptr,则代表parent为root_root = cur;cur->_parent = nullptr;}parent->_bf = 0;cur->_bf = 0;
}
②左旋:
当继续向上更新到父节点平衡因子是2时,则需要左旋.
因为右边比左边高,需要旋转到左边,使其平衡.
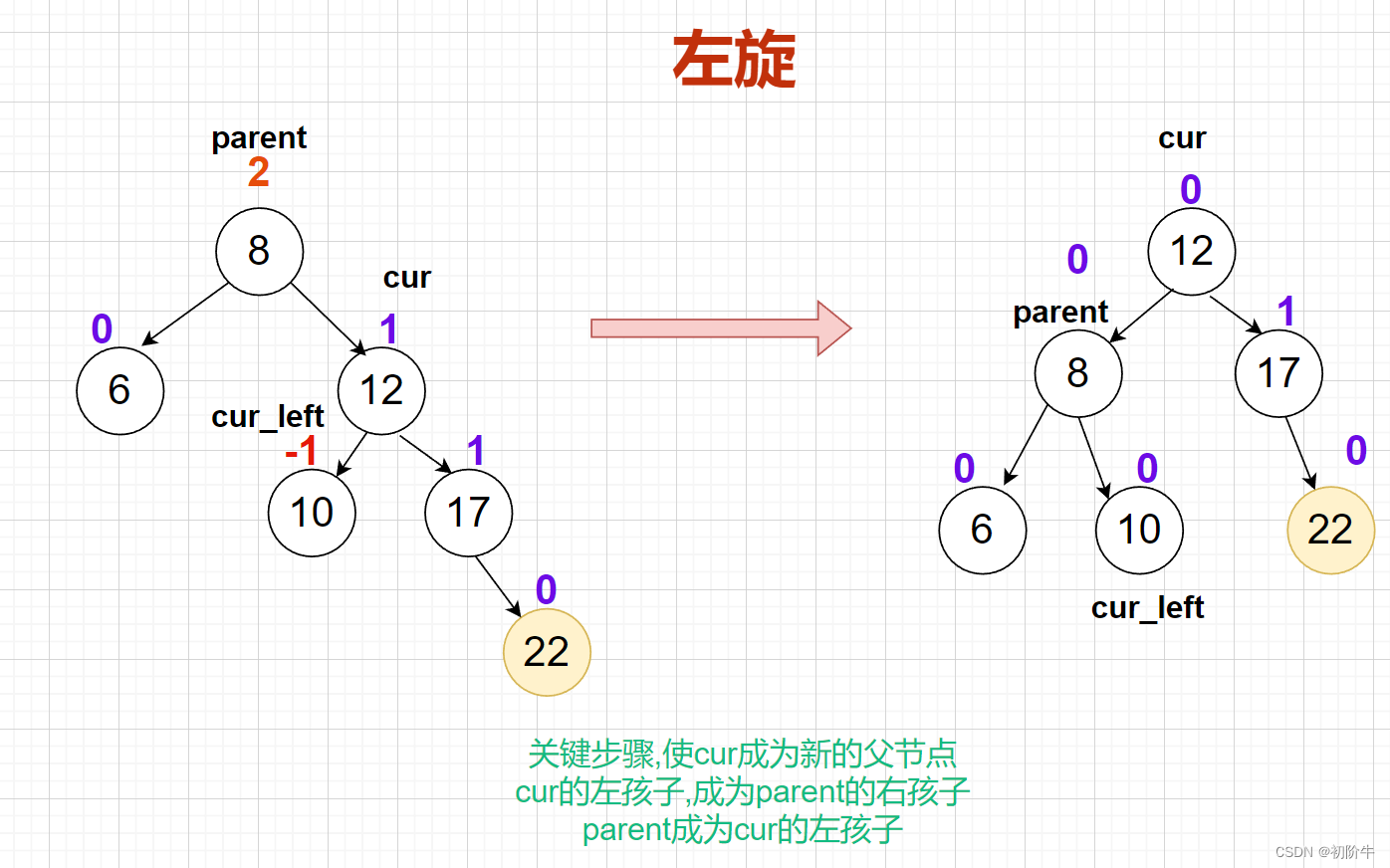
(1)左旋具体图:
关键步骤:
使
cur成为新的父节点
cur的左孩子,成为parent的右孩子
parent成为cur的左孩子
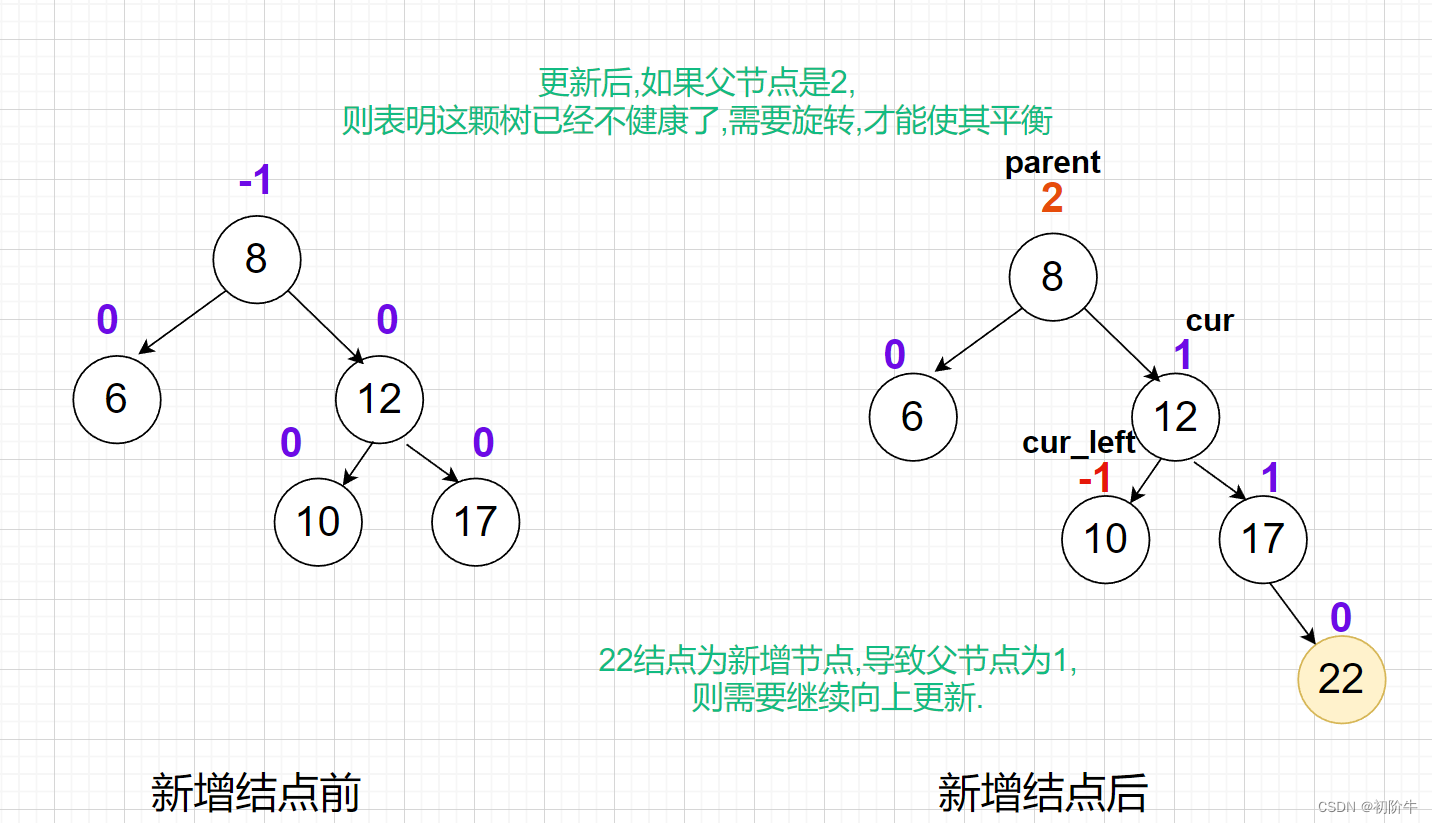
(2)左旋抽象图
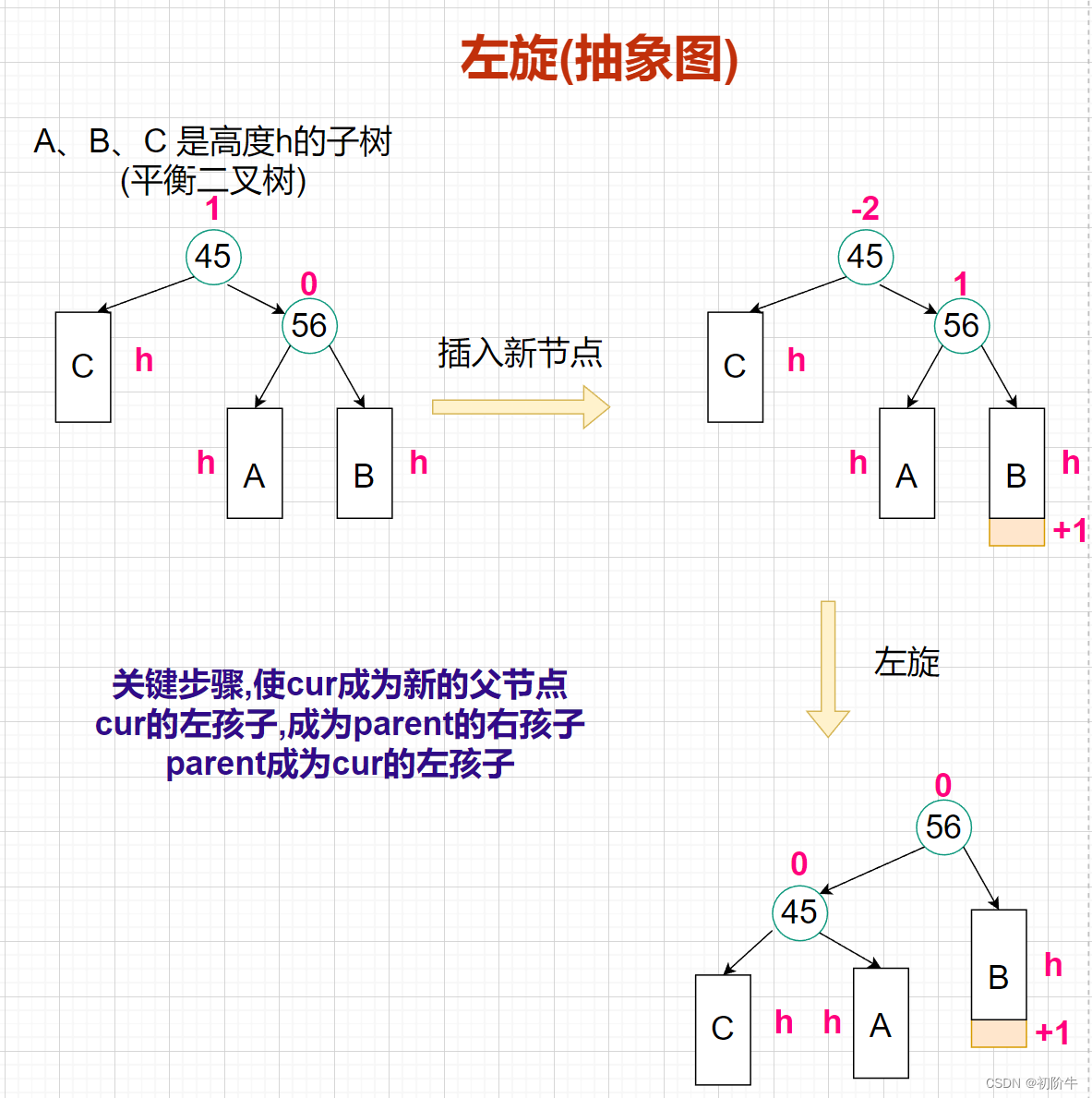
更新平衡因子:
从抽象图可以看出,左旋旋转后,平衡因子cur parent都可以无脑设置为0.
代码实现:
//左旋
template<class K, class V>
void AVLTree<K, V>::RotateL(Node* parent)
{Node* ppnode = parent->_parent;Node* cur = parent->_right;Node* cur_left = cur->_left;//cur的右子树变成parent的左子树if (cur_left) { //cur_right 可能不存在parent->_right = cur_left;cur_left->_parent = parent;//保持三叉连}else {parent->_right = nullptr;}//parent变成cur的左子树cur->_left = parent;parent->_parent = cur;//保持三叉连if (ppnode) {cur->_parent = ppnode;if (ppnode->_left == parent) { //如果是上面的左子树ppnode->_left = cur;}else {ppnode->_right = cur; //如果是上面的右子树}}else { //如果ppnode是nullptr,则代表parent为root_root = cur;cur->_parent = nullptr;}//更新平衡因子parent->_bf = 0;cur->_bf = 0;
}
③右左双旋
当cur->_bf 的值是-1,并且parent->_bf 的值是 2,如下图15结点,22结点,18结点这般成折线状。
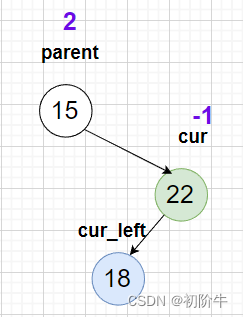
(1)右左双旋具体图
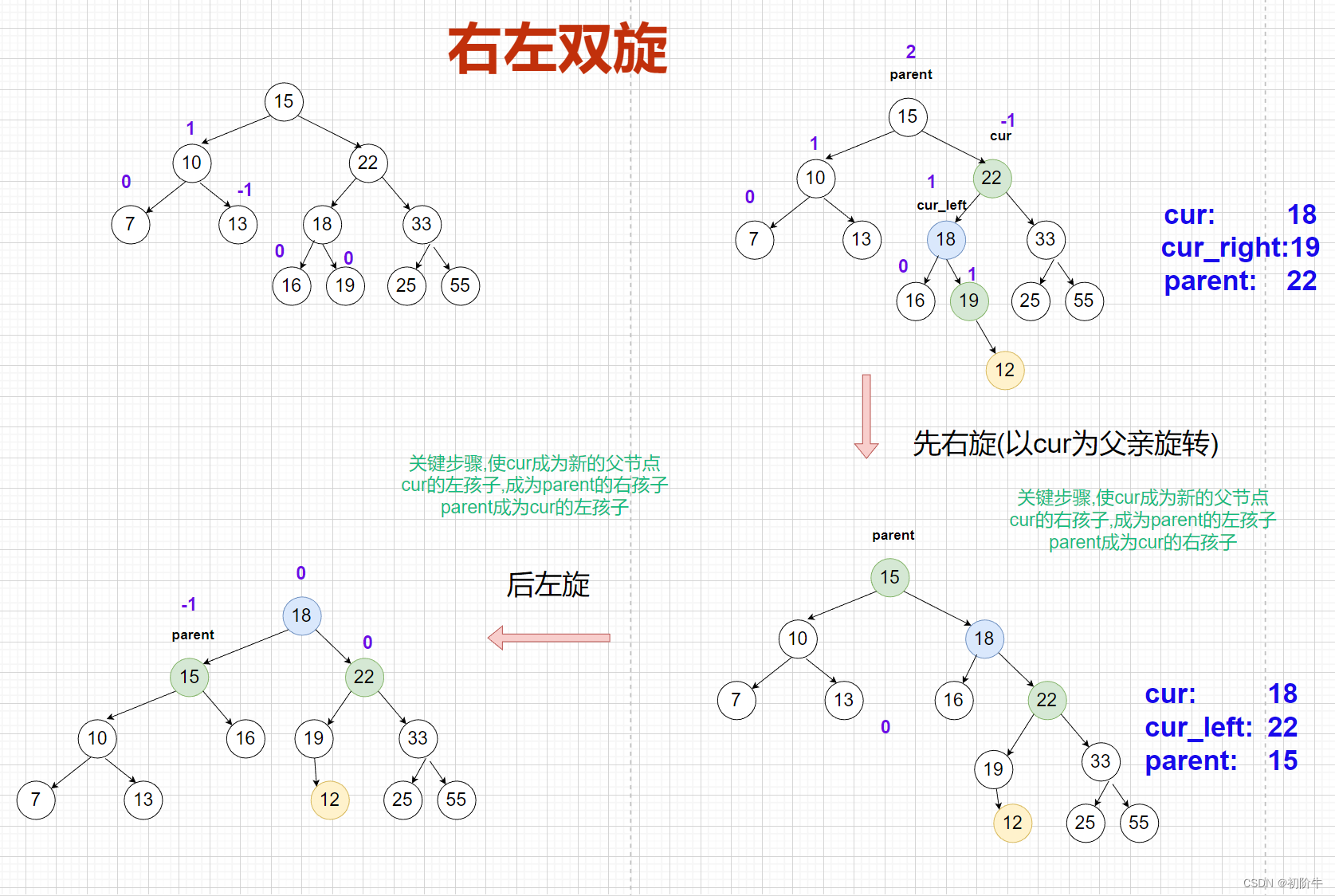
(2)右左双旋抽象图
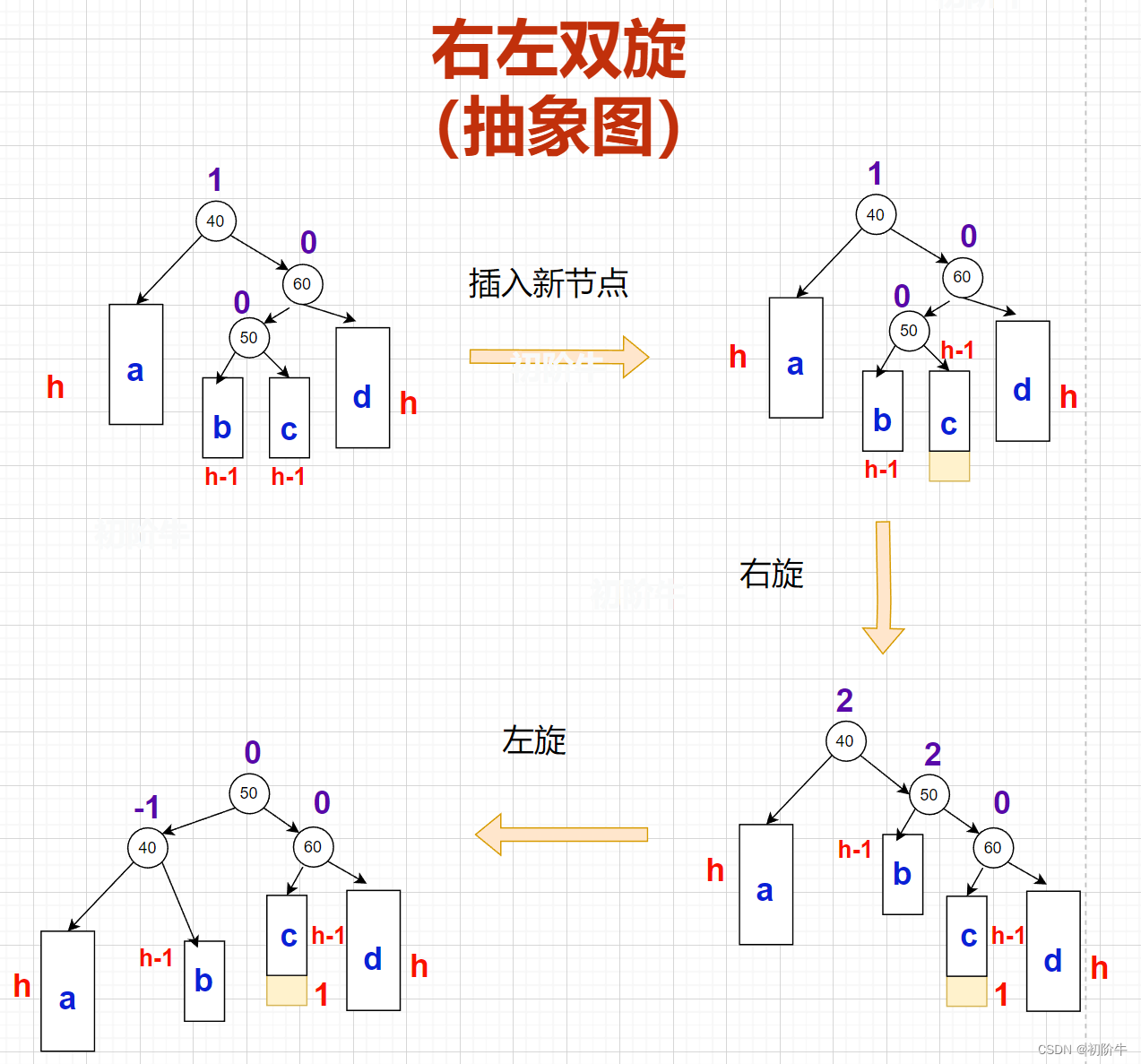
对于双旋,重点在于如何更新平衡因子。
双旋的重点!!!:
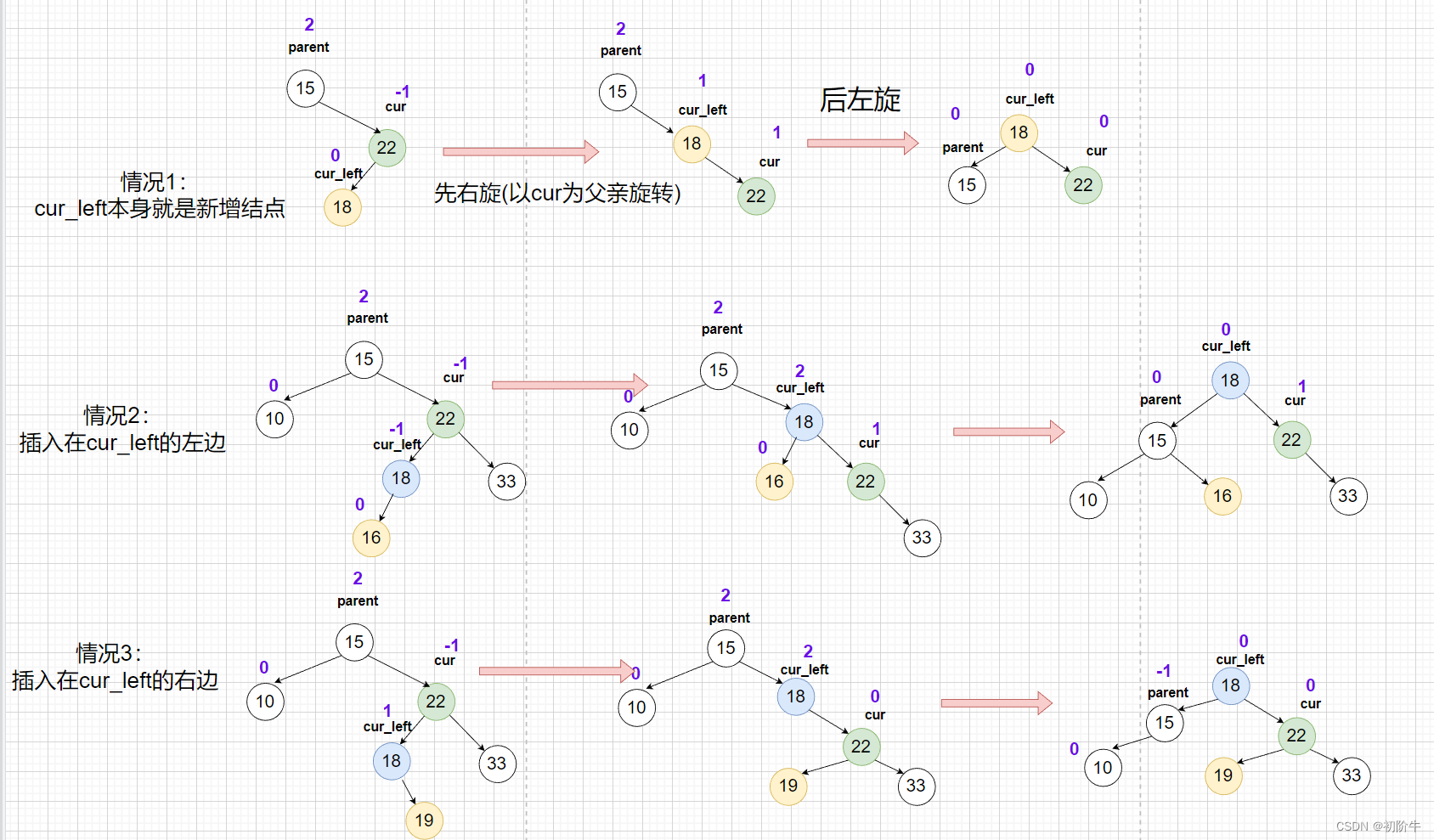
代码实现:
// 右左双旋template<class K, class V>
void AVLTree<K, V>::RotateRL(Node* parent) {Node* cur = parent->_right;Node* cur_left = cur->_left;RotateR(cur); //以parent的right作为新的parent进行右单旋RotateL(parent);//更新平衡因子(最重要)if (cur_left->_bf == 0) { //情况1parent->_bf = 0;cur_left->_bf = 0;cur->_bf = 0;}else if(cur_left->_bf == 1) { //情况3parent->_bf = -1;cur_left->_bf = 0;cur->_bf = 0;}else if (cur_left->_bf == -1) { //情况2parent->_bf = 0;cur_left->_bf = 0;cur->_bf = 1;}else {assert(false);}
}
④左右双旋
与左右双旋类似,这里不过多介绍了,注意更新平衡因子!!!
(1)左右双旋具体图
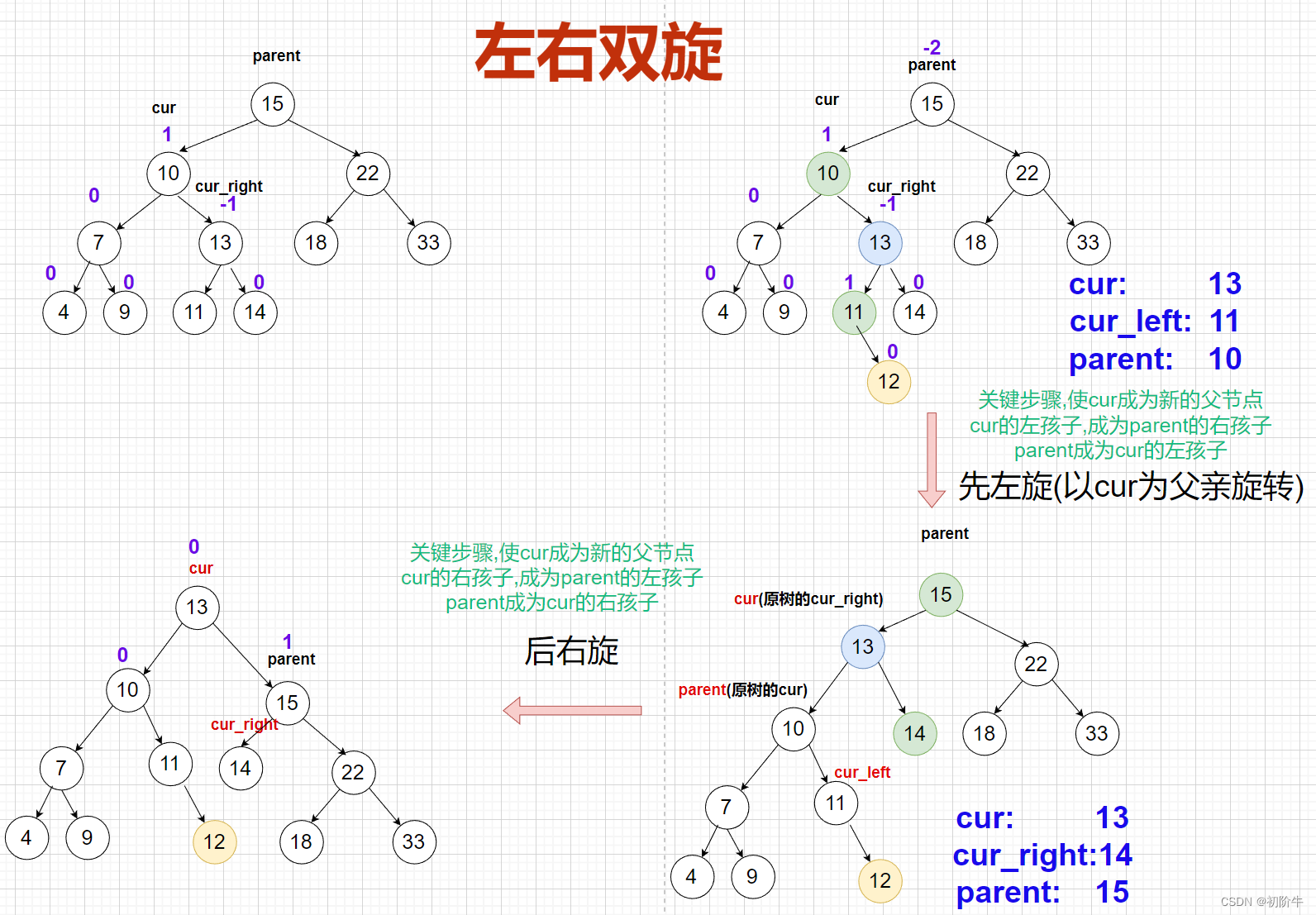
(2)左右双旋抽象图
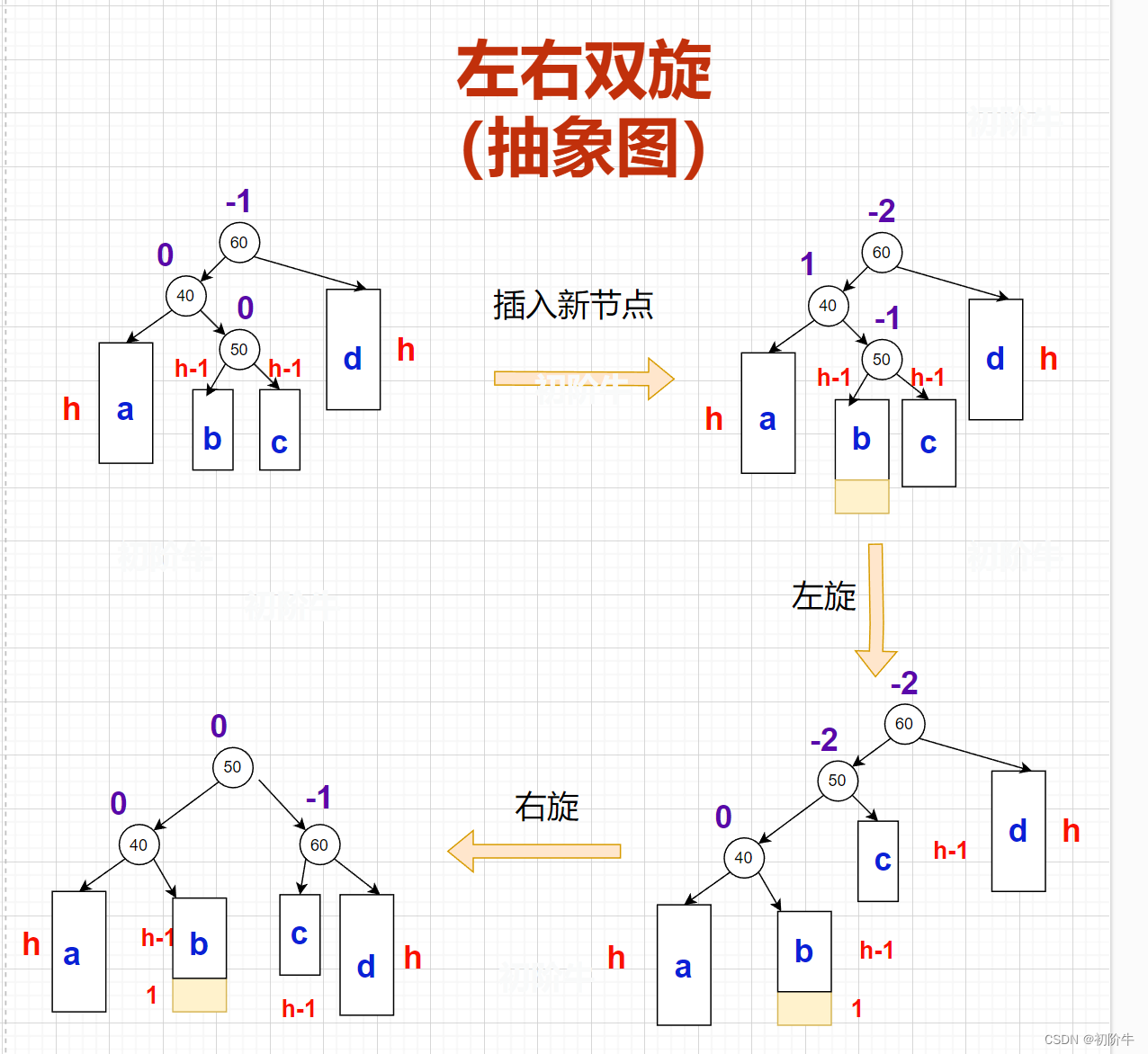
template<class K, class V>
void AVLTree<K, V>::RotateLR(Node* parent) {Node* cur = parent->_left;Node* cur_right = cur->_right;RotateR(cur); //以parent的right作为新的parent进行右单旋RotateL(parent);//更新平衡因子(最重要)if (cur_right->_bf == 0) {parent->_bf = 0;cur_right->_bf = 0;cur->_bf = 0;}else if (cur_right->_bf == 1) {parent->_bf = 0;cur_right->_bf = 0;cur->_bf = -1;}else if (cur_right->_bf == -1) {parent->_bf = 1;cur_right->_bf = 0;cur->_bf = 0;}else {assert(false);}
}
"插入"操作的代码实现:
template<class K,class V>
bool AVLTree<K,V>::Insert(const pair<K, V>& kv)
{if (_root == nullptr) {_root = new Node(kv);return true;}Node* cur = _root, * parent = nullptr;//寻找插入位置while (cur) {parent = cur;if (_root->_kv.first > kv.first) {cur = cur->_left;}else if (_root->_kv.first < kv.first) {cur = cur->_right;}else {return false;}}//判断插入在左边还是右边cur = new Node(kv);if (kv.first < parent->_kv.first){ //插入在左边parent->_left = cur;}else{ //插入在右边parent->_right = cur;}cur->_parent = parent; //保证三叉链的关系//更新平衡因子,最终可能更新到根节点while (parent) { if (cur==parent->_left) { //如果是插入在左边,平衡因子-1parent->_bf--; }else if(parent->_right == cur) { //如果是插入在右边,//平衡因子+1parent->_bf++; }if (parent->_bf == 0) { //平衡了,很健康,不需要往上调整break;}else if (parent->_bf == -1 || parent->_bf == 1) { //表明只是有点感冒,还无伤大雅,继续往上更新.cur = parent;parent = parent->_parent;}else if (parent->_bf == -2 || parent->_bf == 2) { //此时已经不平衡了,需要旋转//左边高,右单旋if (cur->_bf == -1 && parent->_bf == -2) {RotateR(parent);}else if (cur->_bf == 1 && parent->_bf == 2) { //右边高,左单旋RotateL(parent);}else if (cur->_bf == 1 && parent->_bf == -2) { //左右双旋RotateLR(parent);}else if (cur->_bf == -1 && parent->_bf == 2) { //右左双旋RotateRL(parent);}}}return true;
}2.2 中序遍历:
由于中序遍历需要传参 参数为根节点,而根节点是私有成员变量,所以这里用再套一层函数的方法,是一个不错的设计。
template<class K, class V>
void AVLTree<K, V>::_InOrder(Node* root)
{if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << "->" << root->_kv.second << endl;_InOrder(root->_right);
}template<class K, class V>
void AVLTree<K, V>::InOrder()
{if (_root == nullptr){cout << "空树" << endl;return;}_InOrder(_root);
}
2.3 AVL树的"高度"
同求二叉树的高度没有啥区别。
需要注意的是:
1处和2处,需要记录左右子树的根否则后面的都需要重新大量的重复计算。
template<class K, class V>
size_t AVLTree<K, V>::_Height(Node* root)
{if (root == nullptr)return 0;int leftHeight = _Height(root->_left); //1int rightHeight = _Height(root->_right); //2return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
2.4 验证AVL树
判断每棵树的平衡因子是否=右子树-左子树的高度即可。
template<class K, class V>
bool AVLTree<K, V>::_IsAVLTree(Node* root) {if (root == nullptr)return true;int leftHight = _Height(root->_left);int rightHight = _Height(root->_right);if (rightHight - leftHight != root->_bf){cout << "平衡因子异常:" << root->_kv.first << "->" << root->_bf << endl;return false;}return abs(rightHight - leftHight) < 2&& _IsAVLTree(root->_left)&& _IsAVLTree(root->_right);
}
结语
AVL树的平衡性使得它的插入、删除和查找操作的时间复杂度都是O(logn),与红黑树相当。然而,由于AVL树在每次插入或删除时都需要进行平衡调整,所以它的常数比红黑树稍大,因此在实际应用中,红黑树更为常用。
后续会更新红黑树的介绍,很多人认为红黑树是比AVL树还要优秀的结构,不想要了解一下吗? 还请保持关注哦!

相关文章:

会旋转的树,你见过吗?
🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨ 🐻强烈推荐优质专栏: 🍔🍟🌯C的世界(持续更新中) 🐻推荐专栏1: 🍔🍟🌯C语言初阶 🐻推荐专栏2: 🍔…...

Azure Machine Learning - 提示工程简介
OpenAI的GPT-3、GPT-3.5和GPT-4模型基于用户输入的文本提示工作。有效的提示构造是使用这些模型的关键技能,涉及到配置模型权重以执行特定任务。这不仅是技术操作,更像是一种艺术,需要经验和直觉。本文旨在介绍适用于所有GPT模型的提示概念和…...

服务器的安全包括哪些方面?服务器安全该如何去加固处理?
服务器安全包括如下几个方面: 系统安全:包括操作系统的安全性、系统的漏洞和补丁管理、用户管理、文件权限和访问控制等。 网络安全:包括网络拓扑结构、网络设备的安全性、网络协议的安全性、防火墙和入侵检测等。 数据安全:包括数…...
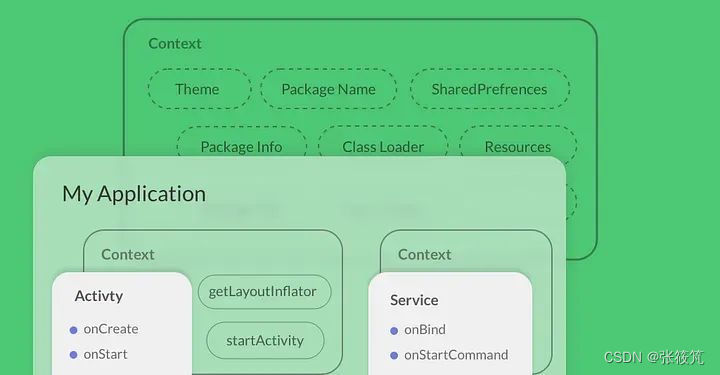
为什么在Android中需要Context?
介绍 在Android开发中,Context是一个非常重要的概念,但是很多开发者可能并不清楚它的真正含义以及为什么需要使用它。本文将详细介绍Context的概念,并解释为什么在Android应用中需要使用它。 Context的来源 Context的概念来源于Android框架…...

AIGC实战——条件生成对抗网络(Conditional Generative Adversarial Net, CGAN)
AIGC实战——条件生成对抗网络 0. 前言1. CGAN架构2. 模型训练3. CGAN 分析小结系列链接 0. 前言 我们已经学习了如何构建生成对抗网络 (Generative Adversarial Net, GAN) 以从给定的训练集中生成逼真图像。但是,我们无法控制想要生成的图像类型,例如控…...

高性能计算HPC与统一存储
高性能计算(HPC)广泛应用于处理大量数据的复杂计算,提供更精确高效的计算结果,在石油勘探、基因分析、气象预测等领域,是企业科研机构进行研发的有效手段。为了分析复杂和大量的数据,存储方案需要响应更快&…...

秋招上岸记录咕咕咕了。
思考了一下,感觉并没有单独写这样一篇博客的必要。 能够写出来的,一些可能会对人有帮助的东西都做进了视频里面,未来会在blbl发布,目前剪辑正在施工中(?) 另外就是,那个视频里面使…...

vue模板语法
一、插值 1、文本 (1)v-text语法 缩写: {{…}}(双大括号)的文本插值 方法一: <template><h1> hello </h1><p v-text"data.name"></p><!-- v-text的简写--&…...
)
Pytorch神经网络的模型架构(nn.Module和nn.Sequential的用法)
一、层和块 在构造自定义块之前,我们先回顾一下多层感知机的代码。下面的代码生成一个网络,其中包含一个具有256个单元和ReLU激活函数的全连接隐藏层,然后是一个具有10个隐藏单元且不带激活函数的全连接输出层。 import torch from torch im…...

JS数组之展开运算符
展开运算符是什么?有什么作用? 展开运算符可以将一个数组展开 const arr [1,2,3,4,5]// 我们使用...展开数组console.log(...arr) //1 2 3 4 5它不会修改原数组 典型运用场景:求数组最大值、最小值、合并数组等 会让我们代码更加简洁 最大值…...

读书笔记:《汽车构造与原理》
《透视汽车会跑的奥秘》《汽车为什么会跑:底盘图解》《汽车为什么会跑:图解汽车构造与原理》 一、心脏:发动机 活塞往复运动转化为曲轴的旋转运动 活塞:膝关节活塞连杆:小腿曲轴:自行车脚踏板 四冲程&…...

INS 量测更新
5 量测更新 5.1 GNSS位置及速度更新 r ^ G P S , i n r ^ I M U n D R − 1 C b n l b v ^ G P S , i n v ^ I M U n ω i n n C b n l b − C b n ω i b b l b \begin{aligned} \hat{r}_{GPS,i}^{n} & \hat{r}_{IMU}^{n} D_{R}^{-1}C_{b}^{n} l^b\\ \hat{v}_{GPS…...

【ssh基础知识】
ssh基础知识 常用命令登录流程配置文件ssh密钥登录生成密钥上传公钥关闭密码登录 ssh服务管理查看日志ssh端口转发 ssh(ssh客户端)是一个用于登录到远程机器并在远程机器上执行命令的程序。 它旨在提供安全的加密通信在不安全的网络上的两个不受信任的主…...

04 开发第一个组件
概述 在Vue3中,一个组件就是一个.vue文件。 在本小节中,我们来开发第一个Vue3组件。这个组件的功能非常的简单,只需要在浏览器上输出一个固定的字符串”欢迎跟着Python私教一起学Vue3“即可。 实现步骤 第一步:新增src/compon…...

【Unity】如何让Unity程序一打开就运行命令行命令
【背景】 Unity程序有时依赖于某些服务去实现一些功能,此时可能需要类似打开程序就自动运行Windows命令行命令的功能。 【方法】 using UnityEngine; using System.Diagnostics; using System.Threading.Tasks; using System.IO; using System.Text...
Web前端-HTML(表格与表单)
文章目录 1.表格与表单1.1 概述 2.表格 table2.1 表格概述2.2. 创建表格2.3 表格属性2.4. 表头单元格标签th2.5 表格标题caption(了解)2.6 合并单元格(难点)2.7 总结表格 3. 表单标签(重点)3.1 概述3.2 form表单3.3 input 控件(重点)type 属性value属性值…...

Android RecycleView实现平滑滚动置顶和调整滚动速度
目录 一、滑动到指定位置(target position)并且置顶 1. RecycleView默认的几个实现方法及缺陷 2. 优化源码实现置顶方案 二、调整平移滑动速率 三、其他方案:置顶、置顶加偏移、居中 1. 其他置顶方案 2. 置顶加偏移 3. 滚动居中 在实…...

跳跃游戏 + 45. 跳跃游戏 II
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 示例 1: 输…...
)
在Django中使用多语言(i18n)
在Django中使用多语言 配置中间件 MIDDLEWARE [......django.contrib.sessions.middleware.SessionMiddleware,django.middleware.locale.LocaleMiddleware, # 此行重点django.middleware.common.CommonMiddleware,...... ]配置翻译文件目录 根目录下创建目录locale # 国…...
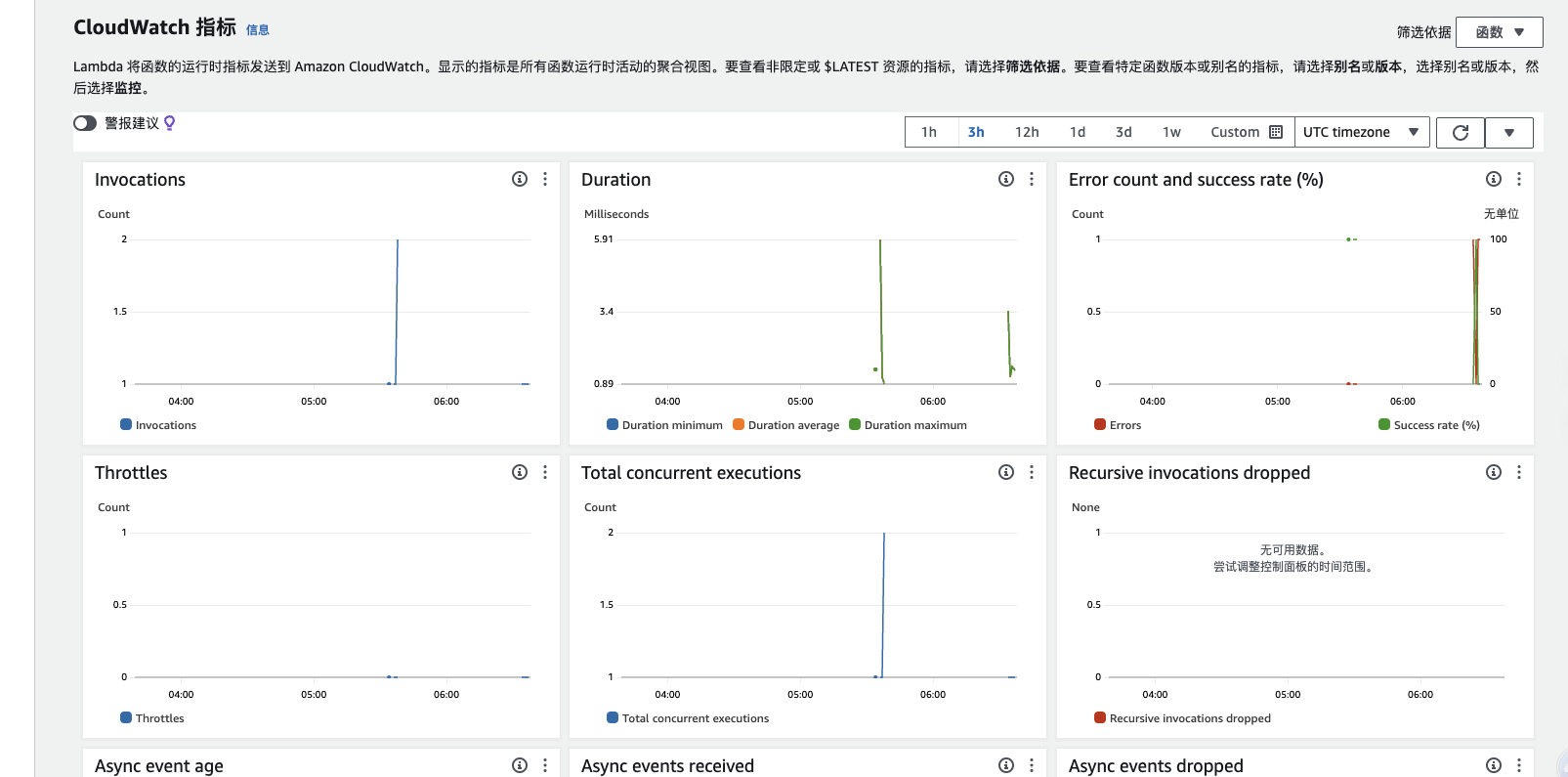
高性价比AWS Lambda无服务体验
前言 之前听到一个讲座说到AWS Lambda服务,基于Serverless无服务模型,另外官网还免费提供 100 万个请求 按月,包含在 AWS 免费套餐中是真的很香,对于一些小型的起步的网站或者用户量不大的网站,简直就是免费ÿ…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...