【数据结构】八大排序之直接插入排序算法
🦄个人主页:修修修也
🎏所属专栏:数据结构
⚙️操作环境:Visual Studio 2022

一.直接插入排序简介及思路
直接插入排序(Straight Insertion Sort)是一种简单直观的插入排序算法.
它的基本操作是:
- 将一个数据插入到已经排好的有序表中,从而得到一个新的,数据数增1的有序表.
- 直到所有的数据插入完为止,得到一个新的有序序列.
在实际生活中,我们玩扑克牌时就使用了插入排序的思想:
算法动图演示如下:
二.直接插入排序的代码实现
算法实现步骤:(以升序为例)
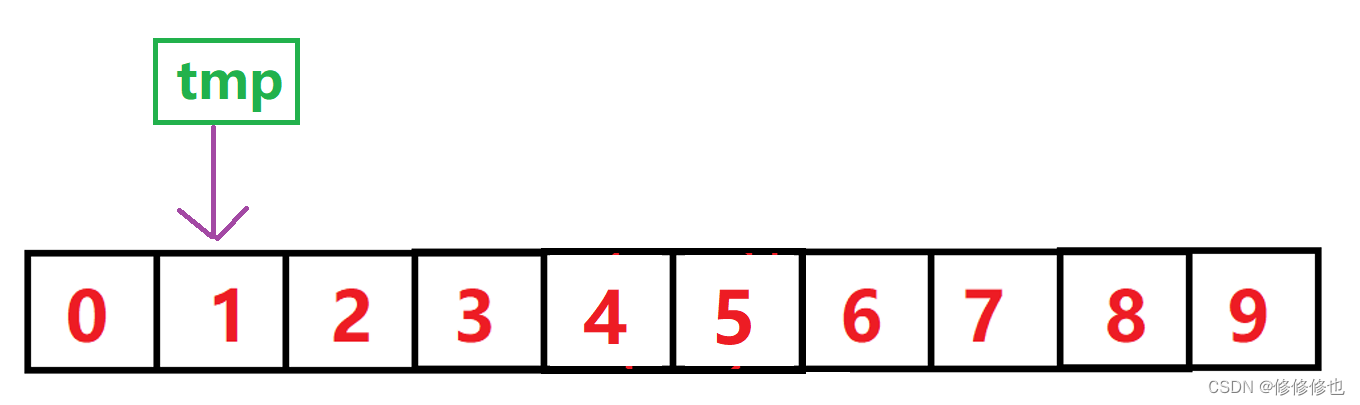
- 当表中只有第一个数据的时候它是一定有序的,因此我们从第二个元素开始向前面的有序表"插入"数据.
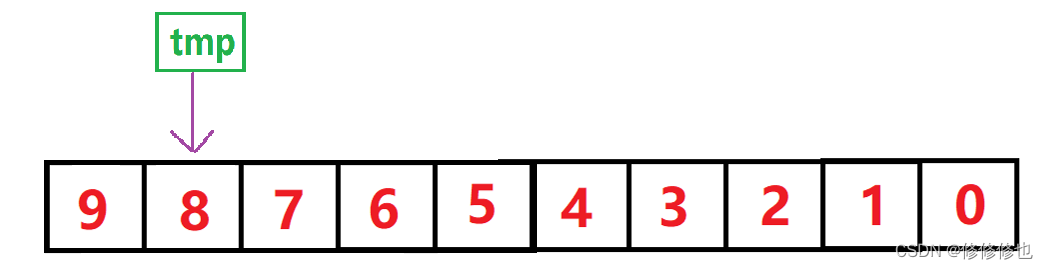
- 具体插入方式,使用tmp记录下当前待插入元素,然后tmp从后向前与有序表中的元素逐一比对,如果tmp小于比对元素,则比对元素向后挪动一个位置.
- 直到tmp不小于比对元素时,将tmp插入到比对元素后面.
- 循环将数据向前插入,直到将待排数组的所有数据元素都插入进有序表,排序完成.
清楚了逻辑和概念后,我们的代码实现就比较简单了.代码如下:
//插入排序(升序
void InsertSort(int* a, int n)
{for (int i = 1; i < n; i++){int end = i - 1;int tmp = a[i];//将tmp插入到[0,end]这个有序表的区间里while (end >= 0){if (tmp < a[end]) //如果tmp小于比对元素,将比对元素向后挪{a[end + 1] = a[end];end--;}else //如果tmp不小于比对元素,将tmp插入到比对元素后面{break;}}a[end + 1] = tmp;}
}三.直接插入排序的时间复杂度分析
📌最好情况时间复杂度
直接排序的最好情况是每个tmp向前插入时都发现自己恰好不小于前面有序表中的最后一个元素,这时就直接将自己放在自己原本的地方就可以继续向前插入下一个元素了,即数组完全顺序的情况:
易得此时的:
- 算法执行次数为:
- 算法时间复杂度为:
📌最坏情况时间复杂度
直接插入的最坏情况是遇到每一个tmp都直到比对到前面有序表的0号位置才插入,即数组完全逆序的情况:
此时算法每趟的交换次数累加起来就是1 + 2 + ...... +(n-2)+(n-1),可以发现当算法执行结束,所有次数累加起来恰好是一个等差数列,我们利用求和公式可得:
- 算法执行总次数为:
- 算法时间复杂度为:
四.直接插入排序的优化
我们通过对前面直接插入排序的分析可以发现,当数组整体完全逆序时:
算法的执行总次数为:
算法的执行总次数为:
但是如果我们面对的是前后两部分分别逆序的数组时:
算法的执行总次数为:
算法的执行总次数为:
此时算法的效率就提高了:
如果我们再分为前后四部分逆序的数组时:
算法的执行总次数为:
算法的执行总次数为:
此时算法的效率又提高了:
通过前面的分析,我们可以发现,随着我们分的部分的增加,算法的执行次数在有规律的减少:
分成k部分与算法执行总次数有如下关系:
如果我们令k无限大,此时算法的执行次数就可以忽略n^2项,而只剩下1/2n项了
其实k无限大的情况,就是数组被分为只有前后两个元素逆序的情况:
这种情况下,算法的执行总次数:(1+1+......+1+1)
算法的执行总次数:
通过上面的分析,我们可以得到一个结论:
当数组元素越接近基本有序,直接插入排序算法的时间复杂度就会越低.
那么我们是不是可以在正式进行插入排序之前将数组元素先简单"预排序"一下呢,即在预排序中,我们尽量将大一些的元素放在数组靠后的位置,小一些的元素放在数组靠前的位置,这样再进行直接插入排序就能使效率提高很多.
如果你能够理解这一直接插入排序算法的优化思路,那么恭喜你,你已经理解了希尔排序的思想,接下来我会在另一篇博客中,详细介绍怎样通过这一思路优化直接插入排序算法,最终构造出非常著名的希尔排序算法.
感兴趣的朋友可以直接点击下方文章链接查看希尔排序算法的相关内容:
【数据结构】八大排序之希尔排序
https://blog.csdn.net/weixin_72357342/article/details/135043566
结语
希望这篇直接插入排序算法详解能对大家有所帮助,欢迎大佬们留言或私信与我交流.
有关更多排序相关知识可以移步:
【数据结构】八大排序算法![]() https://blog.csdn.net/weixin_72357342/article/details/135038495?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22135038495%22%2C%22source%22%3A%22weixin_72357342%22%7D&fromshare=blogdetail
https://blog.csdn.net/weixin_72357342/article/details/135038495?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22135038495%22%2C%22source%22%3A%22weixin_72357342%22%7D&fromshare=blogdetail
学海漫浩浩,我亦苦作舟!关注我,大家一起学习,一起进步!
相关文章推荐
【数据结构】八大排序之冒泡排序算法
【数据结构】八大排序之希尔排序算法
......
数据结构排序算法篇思维导图:

相关文章:

【数据结构】八大排序之直接插入排序算法
🦄个人主页:修修修也 🎏所属专栏:数据结构 ⚙️操作环境:Visual Studio 2022 一.直接插入排序简介及思路 直接插入排序(Straight Insertion Sort)是一种简单直观的插入排序算法. 它的基本操作是: 将一个数据插入到已经排好的有序表中,从而得到一个新的,数…...

网络编程『socket套接字 ‖ 简易UDP网络程序』
🔭个人主页: 北 海 🛜所属专栏: Linux学习之旅、神奇的网络世界 💻操作环境: CentOS 7.6 阿里云远程服务器 文章目录 🌤️前言🌦️正文1.预备知识1.1.IP地址1.2.端口号1.3.端口号与进…...

FreeSWITCH rtp endpoint recvonly
查了下rtp.c的源码,远端端口为0就意味着recvonly,但其实不然,调用switch_rtp_new会马上返回失败 经过反复测试,增加下面几行代码之后终于变成了recvonly: tech_pvt->mode RTP_RECVONLY; rtp_flags[SWITCH_RTP_FLAG_AUTOADJ];…...
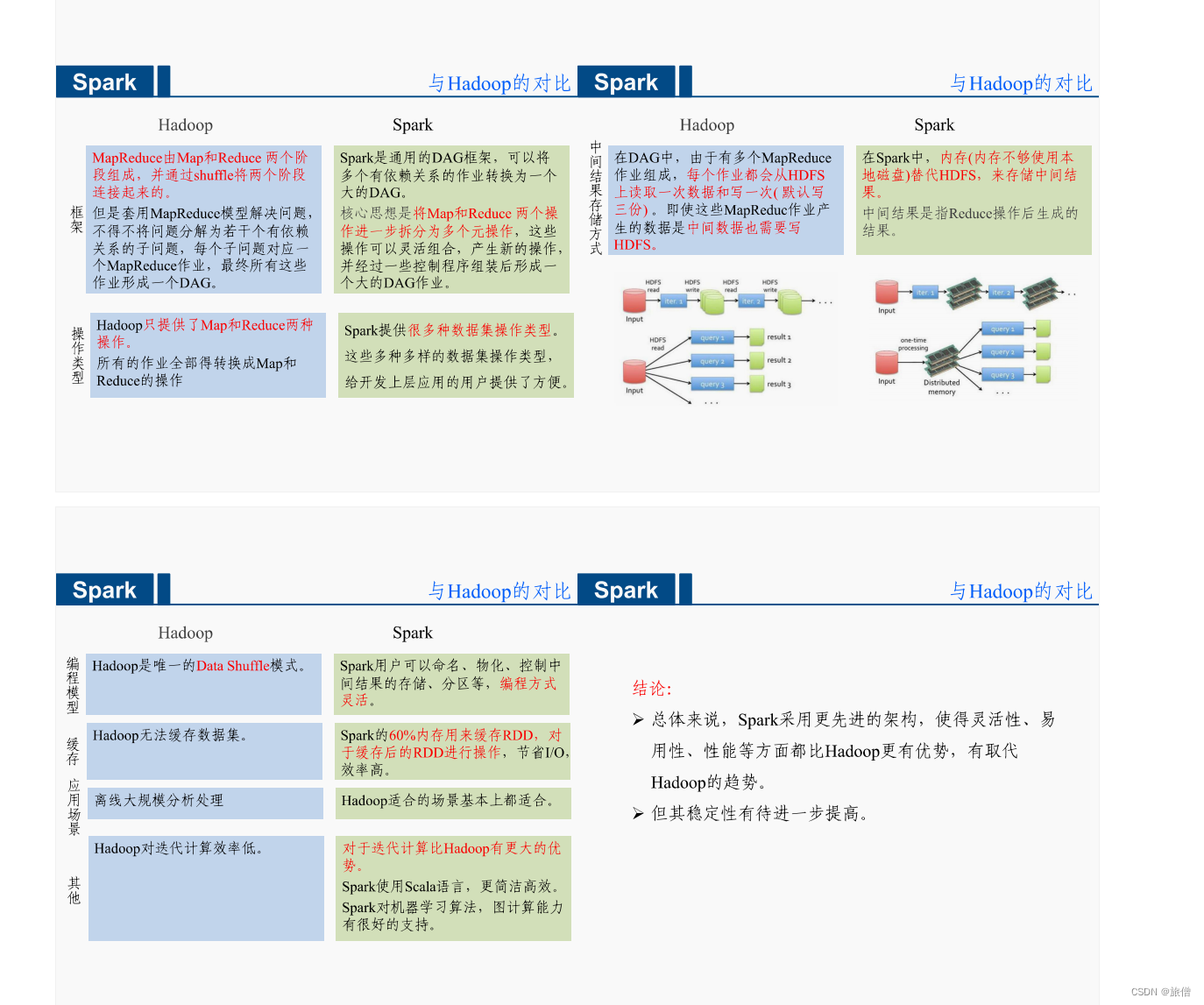
Hadoop和Spark的区别
Hadoop 表达能力有限。磁盘IO开销大,延迟度高。任务和任务之间的衔接涉及IO开销。前一个任务完成之前其他任务无法完成,难以胜任复杂、多阶段的计算任务。 Spark Spark模型是对Mapreduce模型的改进,可以说没有HDFS、Mapreduce就没有Spark。…...
英文论文降重修改技巧 papergpt
大家好,今天来聊聊英文论文降重修改技巧,希望能给大家提供一点参考。 以下是针对论文重复率高的情况,提供一些修改建议和技巧,可以借助此类工具: 英文论文降重修改技巧 作为网站编辑,我们经常需要处理大量…...
DevOps搭建(十)-安装Harbor镜像仓库详细步骤
1、下载Harbor 官方地址: https://goharbor.io/ 下载地址: https://github.com/goharbor/harbor/tags 选择文档版本进行下载,这里我们选择v2.7.2版本 2、上传到服务器并解压 上传压缩包到服务器后,解压到/usr/local目录下&a…...
DDA 算法
CAD 算法是计算机辅助设计的算法,几何算法是解决几何问题的算法 CAD 算法是指在计算机辅助设计软件中使用的算法,用于实现各种设计和绘图功能,CAD 广泛应用于建筑、机械、电子等领域,可以大大提高设计效率和精度 绘图算法是 CAD…...
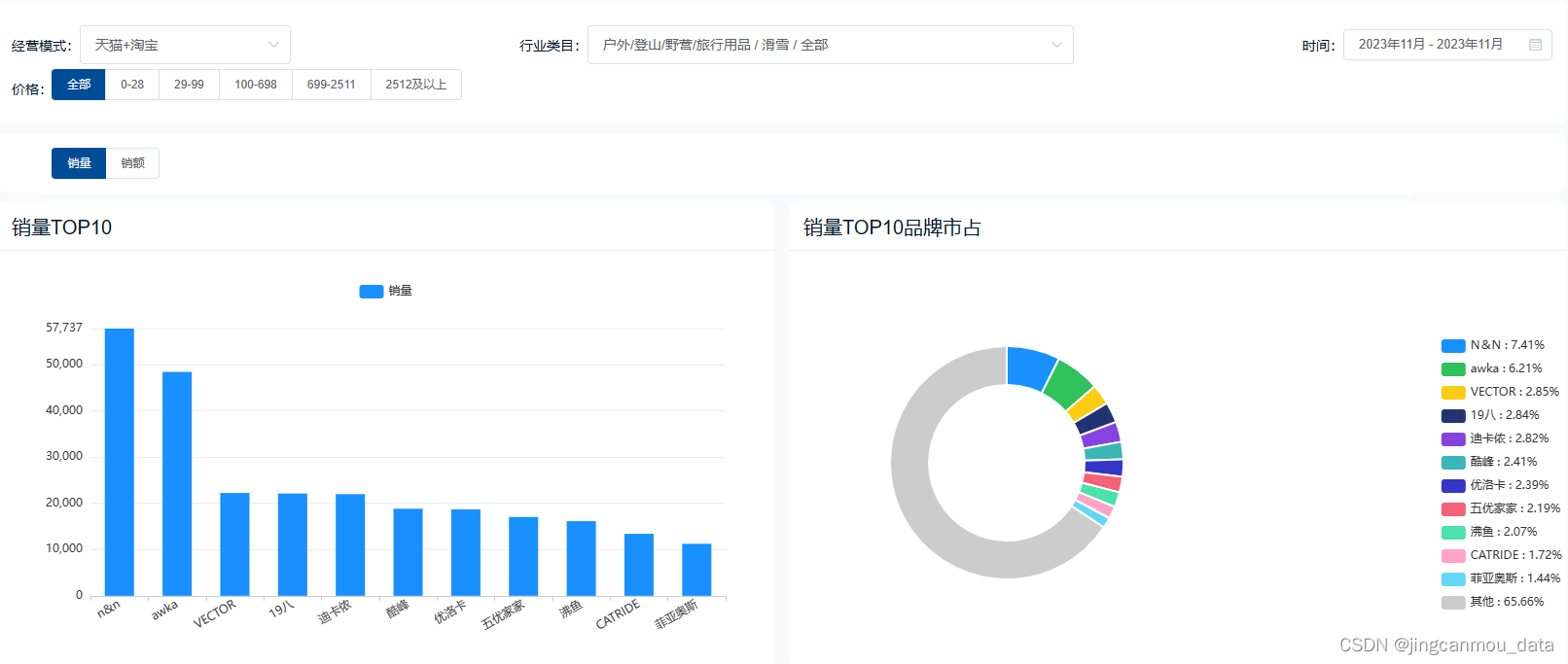
天猫数据平台-淘宝天猫数据-天猫销售数据分析:11月天猫平台滑雪运动装备行业销量翻倍!
随着天气变冷、冬季来临,迎来了疫情后的首个滑雪季,加之自冬奥会结束以来,大众参与冰雪运动的热度持续攀升,因此,冰雪运动的需求正集中释放。 根据相关数据显示,11月以来,全国滑雪场门票预订量较…...

使用OpenCV和PIL库读取图片的区别
OpenCV 和 PIL(Pillow)是两个不同的图像处理库,它们使用不同的数据结构来表示图像。 OpenCV 格式图像: OpenCV 中的图像通常表示为 NumPy 数组。这些数组可以是多维的,例如对于彩色图像,它们是三维数组&am…...
Amazon CodeWhisperer:AI 编程助手
文章作者:prigioni 1. 什么是 Amazon CodeWhisperer? Amazon CodeWhisperer 能够理解以自然语言(英语)编写的注释,并能实时生成多条代码建议,以此提高开发人员生产力。该服务可以直接在集成开发环境&#…...
Linux 使用 Anaconda+Uwsgi 部署 Django项目和前端项目
一、安装Anaconda 使用Anaconda创建python环境的优点: virtualenv只能创建系统原有的python版本,而不能创建创建任意版本的环境 而Anaconda的虚拟环境中,你可以指定任意现存可使用的python环境(包括比原环境版本高的python版本&a…...

分析若依的文件上传处理逻辑
分析若依的文件上传处理逻辑 注:已经从若依框架完成拆分,此处单独分析一下人家精彩的封装,也来理解一下怎么做一个通用的上传接口!如有分析的,理解的不透彻的地方,大家多多包含,欢迎批评指正&am…...

Note3---初阶二叉树~~
目录 前言🍄 1.树概念及结构☎️ 1.1 树的概念🎄 1.2 树的相关概念🦜 1.2.1 部分概念的加深理解🐾 1.2.2 树与非树🪴 1.3 树的表示🎋 1.4 树在实际中的运用(表示文件系统…...

ElasticSearch学习篇8_Lucene之数据存储(Stored Field、DocValue、BKD Tree)
前言 Lucene全文检索主要分为索引、搜索两个过程,对于索引过程就是将文档磁盘存储然后按照指定格式构建索引文件,其中涉及数据存储一些压缩、数据结构设计还是很巧妙的,下面主要记录学习过程中的StoredField、DocValue以及磁盘BKD Tree的一些…...

ROS机器人入门
http://www.autolabor.com.cn/book/ROSTutorials/ 1、ROS简介 ROS 是一个适用于机器人的开源的元操作系统。其实它并不是一个真正的操作系统,其 底层的任务调度、编译、寻址等任务还是由 Linux 操作系统完成,也就是说 ROS 实际上是运 行在 Linux 上的次级…...

30. 深度学习进阶 - 池化
Hi,你好。我是茶桁。 上一节课,我们详细的学习了卷积的原理,在这个过程中给大家讲了一个比较重要的概念,叫做input channel,和output channel。 当然现在不需要直接去实现, 卷积的原理PyTorch、或者TensorFlow什么的…...

工业应用新典范,飞凌嵌入式FET-D9360-C核心板发布!
来源:飞凌嵌入式官网 当前新一轮科技革命和产业变革突飞猛进,工业领域对高性能、高可靠性、高稳定性的计算需求也在日益增长。为了更好地满足这一需求,飞凌嵌入式与芯驰科技(SemiDrive)强强联合,基于芯驰D9…...
Webrtc 学习交流
花了几周的时间研究了一下webrtc ,并开发了一个小项目,用来点对点私密聊天 交流传输文件等…后续会继续扩展其功能。 体验地址,大狗子的ID,我在线时可以连接测试到我 f3e0d6d0-cfd7-44a4-b333-e82c821cd927 项目特点 除了交换信令与stun 没…...

华为云之轻松搭建 Nginx 静态网站
华为云之轻松搭建 Nginx 静态网站 一、本次实践介绍1. 本次实践目的2. 本次实践环境 二、ECS弹性云服务器介绍三、准备实践环境1. 预置环境2. 查看ECS服务器的账号密码信息3. 登录华为云4. 远程登录ECS服务器 四、安装配置 Nginx1. 安装nginx2. 启动nginx3. 浏览器中访问nginx服…...

【pytorch】图像运行过程中,保证梯度情况下变换
部分操作是危险的,会中断梯度流。 self.patch_transformer(adv_patch, lab_batch, img_size, do_rotateTrue, rand_locFalse)p_img_batch self.patch_applier(img_batch, adv_batch_t) # torch.Size([56, 3, 329, 416])可行危险操作 torch.clamp(adv_batch, 0…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...