小信砍柴的题解
目录
原题描述:
时间:1s 空间:256M
题目描述:
输入格式:
输出格式:
样例1输入:
题目大意:
主要思路:
注意事项:
总代码:
原题描述:
时间:1s 空间:256M
题目描述:
小信家里有段木材,初始长度表示为数组
。他可以进行以下填补操作至多
次(可以不操作):
选择两段木材,将
长度截
补到
上,即操作后
,
。
填补操作后,小信要将木材都砍成相同长度的小段,并且不能有剩余,请你告诉他最长的小段能有多长?
输入格式:
第一行包含两个整数表示木材数和操作数。
第二行包含个整数
,表示每段木材的初始长度。
输出格式:
输出一个整数,表示最长的小段的长度。
样例1输入:
2 1
15 9
样例1输出:
8
样例2输入:
2 10
15 9
样例2输出:
24
约定与提示:
对于100%的数据,。
样例1解释:选择操作之后序列变成
,能切成
根长度为
的木材。
样例2解释:选择 操作
次之后序列变成
,能切成
根长度为
的木材。
题目大意:
就是给你一个数组,然你可以操作最多m次,每次操作可以将一个数-1,另一个数+1,最后问你所有数的最大共约数(就是gcd)
主要思路:
直接上思维导图:
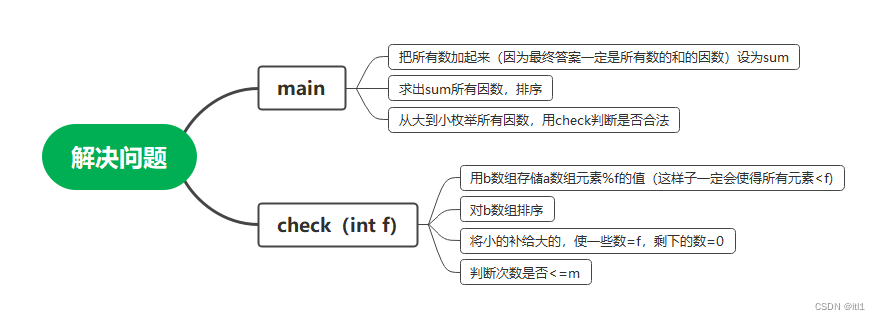
说一下几个重点,给上代码片段:
- 求因数:
int cnt=0;//数组下标 for(int i=1;i*i<=sum;i++)//只要枚举到(sqrt(sum)就可以了 {if(sum%i == 0)//如果是因数 {factor[cnt++] = i;//用来记录因数,放入因数数组中 if(i*i!=sum)//如果不是sum的平方根 {factor[cnt++] = sum/i;//sum/i也是sum的因数 }} } - 将小的补给大的:
int t=0;//记录花费次数 int pos=1;//记录从哪个小的开始补(就是被减的) for(int i=n;i>=1;i--)//枚举大的 {if(b[i]!=0)//如果不是大的(也可以这么理解(被用光了) {int x=f-b[i];//记录要消耗的次数(也是要被补多少) t+=x;//计入次数 while(x>0)//如果还需要补 {if(b[pos]>=x)//如果小的可以补完 {b[pos]-=x;//就补了 break;//跳出 }else{x-=b[pos];//否则就消耗一些要补的 b[pos] = 0;//把小的设成0pos++;//就让下一个小的来补 }}} } /* 直接看不太好看,我演示一遍。当f = 8,b数组为:{1,2,5},pos=1; 先枚举到5。t+=3, x=3。 开始补 第一次发现不可以全补完。 b[pos]也就是b[1]<3,那就耗掉一些。b[1] = 0,x=2,pos=2。 第二次发现可以补完,那就补完,b[2]-=2就是0,跳出。 此时的b数组为:{0,0,5} i枚举到 2时,b[2] == 0了,也就是被用光了,那就跳过。 i枚举到 1时,b[1] == 0了,也就是被用光了,那就跳过。 现在应该理解了吧。 */
注意事项:
不要把check中的b写成a了哦。
第一个合法因数输出后要return 0;
总代码:
#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[510];
int b[510];
int sum;
int factor[10010];//用来记录因数
bool check(int f)
{//千万不要把b写成afor(int i=1;i<=n;i++){b[i] = a[i]%f;}sort(b+1,b+1+n);int t=0;//记录花费次数 int pos=1;//记录从哪个小的开始补(就是被减的) for(int i=n;i>=1;i--)//枚举大的 {if(b[i]!=0)//如果不是大的(也可以这么理解(被用光了) {int x=f-b[i];//记录要消耗的次数(也是要被补多少) t+=x;//计入次数 while(x>0)//如果还需要补 {if(b[pos]>=x)//如果小的可以补完 {b[pos]-=x;//就补了 break;//跳出 }else{x-=b[pos];//否则就消耗一些要补的 b[pos] = 0;//把小的设成0pos++;//就让下一个小的来补 }}}}/*直接看不太好看,我演示一遍。当f = 8,b数组为:{1,2,5},pos=1; 先枚举到5。t+=3, x=3。开始补第一次发现不可以全补完。b[pos]也就是b[1]<3,那就耗掉一些。b[1] = 0,x=2,pos=2。 第二次发现可以补完,那就补完,b[2]-=2就是0,跳出。此时的b数组为:{0,0,5}i枚举到 2时,b[2] == 0了,也就是被用光了,那就跳过。 i枚举到 1时,b[1] == 0了,也就是被用光了,那就跳过。现在应该理解了吧。 */ return t<=m;
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];sum+=a[i];}int cnt=0;//数组下标 for(int i=1;i*i<=sum;i++)//只要枚举到(sqrt(sum)就可以了 {if(sum%i == 0)//如果是因数 {factor[cnt++] = i;//放入因数数组中 if(i*i!=sum)//如果不是sum的平方根 {factor[cnt++] = sum/i;//sum/i也是sum的因数 }}}sort(factor,factor+cnt);for(int i=cnt-1;i>=0;i--)//从大到小枚举,这样子第一个合法因数一定是最大的{if(check(factor[i]))//用来判断每个因数是否合法{cout<<factor[i];return 0;//别忘了return 0;}}return 0;
}相关文章:

小信砍柴的题解
目录 原题描述: 时间:1s 空间:256M 题目描述: 输入格式: 输出格式: 样例1输入: 题目大意: 主要思路: 注意事项: 总代码: 原题描述&#…...
)
华为OD机试 - 跳格子3(Java JS Python C)
题目描述 小明和朋友们一起玩跳格子游戏, 每个格子上有特定的分数 score = [1, -1, -6, 7, -17, 7], 从起点score[0]开始,每次最大的步长为k,请你返回小明跳到终点 score[n-1] 时,能得到的最大得分。 输入描述 第一行输入总的格子数量 n 第二行输入每个格子的分数 sc…...
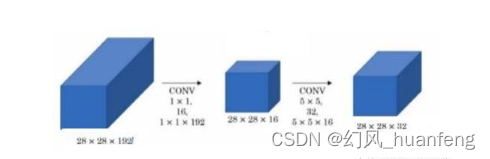
每天五分钟计算机视觉:谷歌的Inception模块的计算成本的问题
计算成本 Inception 层还有一个问题,就是计算成本的问题,我们来看一下55 过滤器在该模块中的计算成本。 原始图片为28*28*192经过32个5*5的过滤操作,它的计算成本为: 我们输出28*28*32个数字,对于输出的每个数字来说,你都需要执行 55192 (5*5为卷积核的大小,192为通道…...
最新AI创作系统ChatGPT系统源码+DALL-E3文生图+支持AI绘画+GPT语音对话功能
一、AI创作系统 SparkAi创作系统是基于ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI…...

78-C语言-完数的判断,以及输出其因子
简介:一个数如果恰好等于它的因子之和,这个数就称为完数,C语言编程找出1000之内的所有完数,并输出其因子。因子可以整除该数字的数, 如6的因子:1 2 3,6%10 6%20 6%30 解释全在注…...
C# 使用FluentHttpClient请求WebApi
写在前面 FluentHttpClient 是一个REST API 异步调用 HTTP 客户端,调用过程非常便捷,采用流式编程,可以将所有请求所需的参数一次性发送,并直接获取序列化后的结果。 老规矩从NuGet上安装该类库: 这边一定要认准是 P…...

AXure交互及案列
AXure交互及案列 1.交互样式简介2.axure交互事件简介3.axure交互动作简介4.axure情形简介2.完成案列1.登录案列2.省市联动案列3.左侧联动 1.交互样式简介 Axure是一种强大的原型设计工具,它允许用户创建高保真的交互式原型,用于演示和测试Web和移动应用…...

美颜SDK技术对比,深入了解视频美颜SDK的工作机制
如何在实时视频中呈现更加自然、美丽的画面,而这正是美颜SDK技术发挥作用的领域之一。本文将对几种主流视频美颜SDK进行深入比较,以揭示它们的工作机制及各自的优劣之处。 随着科技的不断进步,美颜技术已经从简单的图片处理发展到了视频领域…...

OkHttp ,使用 HttpUrl.Builder 来添加查询参数并添加到请求对象
在使用 OkHttp 中,你可以使用 HttpUrl.Builder 来添加查询参数并将其添加到请求对象中。下面是一个示例代码: import okhttp3.HttpUrl; import okhttp3.OkHttpClient; import okhttp3.Request; import okhttp3.Response;public class Main {public stat…...
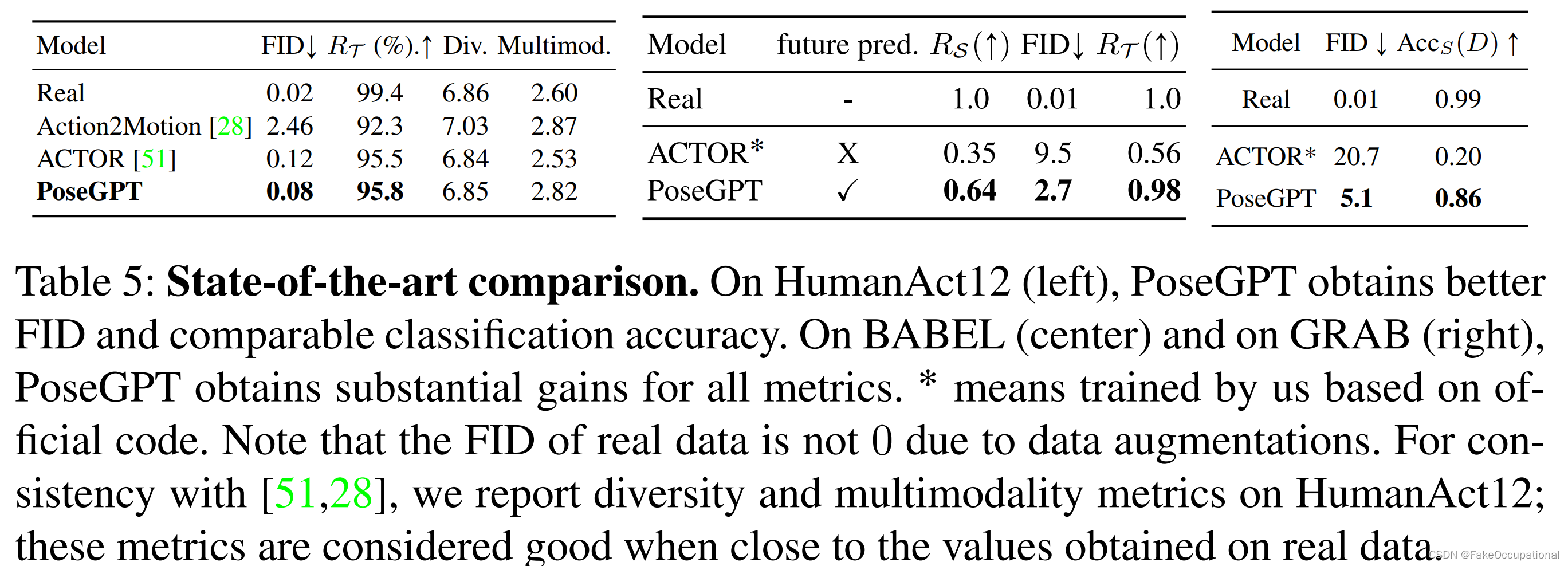
图片速览 PoseGPT:基于量化的 3D 人体运动生成和预测(VQVAE)
papercodehttps://arxiv.org/pdf/2210.10542.pdfhttps://europe.naverlabs.com/research/computer-vision/posegpt/ 方法 将动作压缩到离散空间。使用GPT类的模型预测未来动作的离散索引。使用解码器解码动作得到输出。 效果 提出的方法在HumanAct12(一个标准但小规…...

Java对象结构
Java 对象(Object 实例)结构包括三部分:对象头、对象体、对齐字节。 Object的三个部分 对象头包括三个字段,第一个字段叫做 Mark Word(标记字),用于存储自身运行时的数据 例如 GC 标志位、哈希码、锁状态等信息。 第二个字段叫做 Class Pointer(类对象…...

基于redis的分布式锁实现方案
3. 基于redis的分布式锁实现方案: redis集群,原理是因为redis单线程串行处理. (1). SETNX方案: ①. SETNX(Set if not exists):a. 命令在指定的key不存在时,为key设置指定的值.b. SETNX Key Value设置成功,返回1.设置失败,返回0.c. 没有有效期的②. 原子操作(多个执行命令):Mu…...
基于JAVA+SpringBoot的线上智能问诊就医平台
✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景介绍: 智慧医药系统…...

adb: error: cannot create file/directory ‘d:/1.png‘: No such file or directory
将文件从设备读取到PC 由于权限问题,不能直接pull到电脑磁盘根目录,否则会报错: adb pull <remote> <local> eg: C:\Users\admin>adb pull /sdcard/server.log C:\Users\admin\Desktop /sdcard/server.log: 1 file pulled.…...

Pelee: A Real-Time Object Detection System on Mobile Devices(CVPR 2019)
文章目录 年三十AbstractIntroductionPeleeNet:一个高效的特征提取网络架构消融实验数据集不同设计选择对性能的影响 在ImageNet ILSVRC 2012上的结果真实设备上的速度 Pelee:实时目标检测系统Overview在VOC 2007上的结果不同设计选择的影响与其他框架的比较真实设备…...
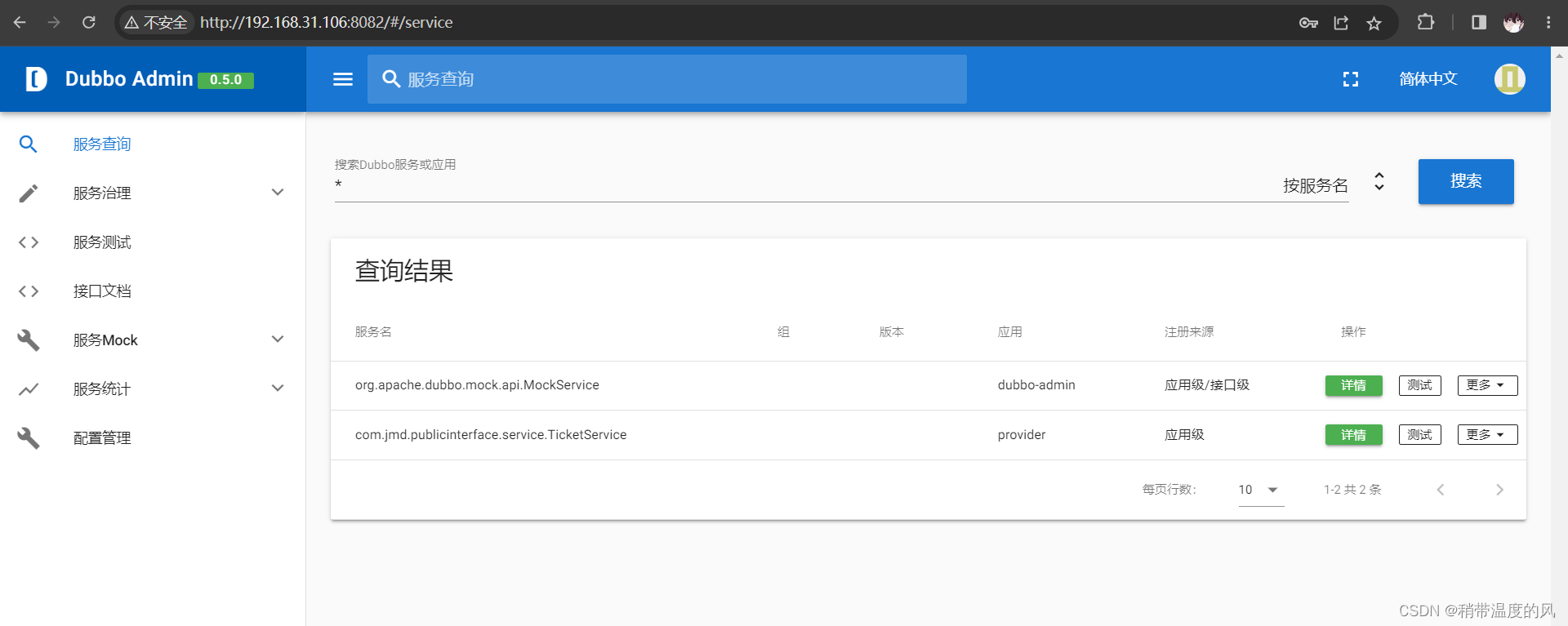
分布式理论 | RPC | Spring Boot 整合 Dubbo + ZooKeeper
一、基础 分布式理论 什么是分布式系统? 在《分布式系统原理与范型》一书中有如下定义:“分布式系统是若干独立计算机的集合,这些计算机对于用户来说就像单个相关系统”; 分布式系统是由一组通过网络进行通信、为了完成共同的…...
局域网其他pc如何访问宿主机虚拟机IP?
文章目录 背景贝瑞蒲公英设置虚拟机网络连接测试 背景 使用贝瑞蒲公英异地组网,将家里的pc作为pgsql服务器在公司使用,但是虚拟机的ip和端口访问不了 贝瑞蒲公英 设置虚拟机网络 就是添加端口转发规则 连接测试 公网内其他pc连接测试 可以看到已经连接成…...

U8 语法制导翻译技术
文章目录 一、总述二、翻译文法1、概念 三、语法制导翻译1、概念2、带属性的翻译文法3)综合属性4)继承属性5)举例 3、 L-属性翻译文法(L-ATG)1)概念2)求值规则 4、简单赋值形式的L-ATGÿ…...

剑指offer A + B
剑指offer A B 题目 输入两个整数,求这两个整数的和是多少。 输入格式 输入两个整数A,B,用空格隔开,0≤A,B≤10的8次幂 输出格式 输出一个整数,表示这两个数的和 样例输入: 3 4样例输出: 7参考答…...
gitlab(gitlab-ce)下载,离线安装
目录 1.下载 2.安装 3.配置 4.启动 5.登录 参考: 1.下载 根据服务器操作系统版本,下载对应的RPM包。 gitlab官网: The DevSecOps Platform | GitLab rpm包官网下载地址: gitlab/gitlab-ce - Results in gitlab/gitlab-ce 国内镜像地…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...
