第7章 排序
前言
在这一章,我们讨论数组元素的排序问题。为简单起见,假设在我们的例子中数组只包含整数,虽然更复杂的结构显然也是可能的。对于本章的大部分内容,我们还假设整个排序工作能够在主存中完成,因此,元素的个数相对来说比较小(小于)。当然,不能在主存中完成而必须在磁盘或磁带上完成的排序也相当重要。这种类型的排序叫作外部排序(external sorting),将在本章末尾讨论外部排序。
我们对内部排序的考察将指出:
- 存在几种容易的算法以
排序,如插入排序。
- 有一种算法叫作希尔排序(Shellsort),它的编程非常简单,以
运行,并在实践中很有效。
- 有一些稍微复杂的
的排序算法。
- 任何通用的排序算法均需要
次比较。
本章的其余部分将描述和分析各种排序算法。这些算法包含一些有趣的、重要的代码优化和算法设计思想。可以对排序做出精确的分析。预先说明,在适当的时候,我们将尽可能地多做一些分析。
7.1 预备知识
我们描述的算法都将是可以互换的。每个算法都将接收一个含有元素的数组和一个包
含元素个数的整数。
我们将假设是传递到排序例程中的元素个数,它已经被检查过,是合法的。按照C
的约定,对于所有的排序,数据都将在位置0处开始。
我们还假设“<”和“>”运算符存在,它们可以用于对输入进行一致的排序。除赋
值运算符外,这两种运算是仅有的允许对输入数据进行的操作。在这些条件下的排序叫作
基于比较的排序(comparison-based sorting)。
7.2 插入排序
7.2.1 算法
最简单的排序算法之一是插入排序(insertion sort)。插入排序由趟(pass)排序组成。对于
趟到
趟,插入排序保证从位置0到位置
上的元素为已排序状态。插入排序利用了这样的事实:位置0到位置
上的元素是已排过序的。图7-1显示一个简单的数组在每一趟插入排序后的情况。
图7-1表达了一般的方法。在第趟,我们将位置
上的元素向左移动到它在前
个元素中的正确位置上。图7-2中的程序实现该想法。第2~5行实现数据移动而没有明显使用交换。将位置
上的元素存于Tmp中,而(在位置
之前)所有更大的元素都向右移动一个位置。然后将Tmp置于正确的位置上。这种方法与实现二叉堆时所用到的技巧相同。

void InsertionSort(ElementType A[], int N)
{int j, P;ElementType Tmp;for (P = 1; P < N; P++){Tmp = A[P];for (j = P; j > 0 && A[j - 1] > Tmp; j--)A[j] = A[j - 1];A[j] = Tmp;}
}![]()
7.2.2 插入排序的分析
由于嵌套循环每趟花费N次迭代,因此插入排序为,而且这个界是精确的,因为以反序输入可以达到该界。精确计算指出对于
的每一个值,第4行的测试最多执行
次。对所有的
求和,得到总数为
另一方面,如果输入数据已预先排序,那么运行时间为,因为内层for循环的检测总是立即判定不成立而终止。事实上,如果输入几乎已排序(该术语将在下一节更严格地定义),那么插入排序将运行得很快。由于这种变化差别很大,因此值得我们去分析该算法平均情形的行为。实际上,和各种其他排序算法一样,插入排序的平均情形也是
,详见下节的分析。
7.3 一些简单排序算法的下界
数字数组的一个逆序(inversion)是指数组中具有但
的序偶(
)。在上节的例子中,输入数据34,8,64,51,32,21有9个逆序,即(34,8),(34,32),(34,21),(64,51),(64,32),(64,21),(51,32),(51,21),(32,21)。这正好是需要由插入排序(非直接)执行的交换次数。情况总是这样,因为交换两个不按原序排列的相邻元素恰好消除一个逆序,而一个排过序的数组没有逆序。由于算法中还有
项其他的工作,因此插入排序的运行时间是
,其中
为原始数组中的逆序数。于是,若逆序数是
,则插入排序以线性时间运行。
我们可以通过计算排列中的平均逆序数而得出插入排序平均运行时间的精确的界。如往常一样,定义平均是一个困难的命题。我们将假设不存在重复元素(如果允许重复,那么我们甚至连重复的平均次数究竟是什么都不清楚)。利用该假设,我们可设输入数据是前个整数的某个排列(因为只有相对顺序才是重要的),并设所有的排列都是等可能的。在这些假设下,我们有如下定理:
定理 7.1 个互异数的数组的平均逆序数是
。
证明:对于含有任意的数的表,考虑其反序表
。上例中的反序表是21,32,51,64,8,34。考虑该表中任意两个数的序偶(x,y),且y>x。显然,恰是
和
之中的一个,该序偶表示一个逆序。在表
和它的反序表
,中序偶的总个数为
。因此,平均表有该量的一半,即
个逆序。
这个定理意味着插入排序平均是二次的,同时也提供了只交换相邻元素的任何算法的一个很强的下界。
定理 7.2 通过交换相邻元素进行排序的任何算法平均需要时间。
证明:初始的平均逆序数 是,而每次交换只减少一个逆序,因此需要
次交换。
这是证明下界的一个例子,它不仅对非显式地实施相邻元素的交换的插入排序有效,而且对诸如冒泡排序和选择排序等其他一些简单算法也是有效的,不过这些算法将不在这里描述。事实上,它对一整类只进行相邻元素的交换的排序算法(包括那些未被发现的算法)都是有效的。正因为如此,这个证明在经验上是不能被认可的。虽然这个下界的证明非常简单,但是一般说来证明下界要比证明上界复杂得多。
这个下界告诉我们,为了使一个排序算法以亚二次(subquadratic)或时间运行,必须执行一些比较,特别要对相距较远的元素进行交换。一个排序算法通过删除逆序得以向前进行,而为了有效地运行,它必须每次交换删除不止一个逆序。
7.4 希尔排序
希尔排序(Shellsort)的名称源于它的发明者Donald Shell,该算法是冲破二次时间屏障的第一批算法之一,不过,从它的发现之日起,又过了若干年后才证明了它的亚二次时间界。正如上节所提到的,它通过比较相距一定间隔的元素来工作,各趟比较所用的距离随着算法的进行而减小,直到只比较相邻元素的最后一趟排序为止。由于这个原因,希尔排序有时也叫作缩小增量排序(diminishing increment sort)。
希尔排序使用一个序列叫作增量序列(increment sequence)。只要
,任何增量序列都是可行的,不过,有些增量序列比另外一些增量序列更好(后面我们将讨论这个问题)。在使用增量
的一趟排序之后,对于每一个
我们有
(这里它是有意义的),所有相隔
的元素都被排序。此时称文件是
-排序的(
-sorted)。例如,图7-3显示了各趟排序后数组的情况。希尔排序的一个重要性质(我们只叙述而不证明)是一个
-排序的文件(此后将是
-排序的)保持它的
-排序性。事实上,假如情况不是这样的话,那么该算法也就没什么意义了,因为前面各趟排序的结果会被后面各趟排序给打乱。

-排序的一般做法是,对于
中的每一个位置
,把其上的元素放到
中间的正确位置上。虽然这并不影响最终结果,但是仔细的考察指出,一趟
-排序的作用就是对
个独立的子数组执行一次插入排序。当我们分析希尔排序的运行时间时,这个考察结果将是很重要的。
增量序列的一种流行(但是不好)的选择是使用Shell建议的序列:和
。图7-4包含一个使用该序列实现希尔排序的程序。后面我们将看到,存在一些递增的序列,它们对该算法的运行时间做出了重要的改进,即使是一个小的改变都可能剧烈地影响算法的性能。
void ShellSort(ElementType A[], int N)
{int i, j, Increment;ElementType Tmp;for (Increment = N / 2; Increment > 0; Increment /= 2)for(i = Increment; i < N; i++){Tmp = A[i];for (j = i; j >= Increment; j -= Increment)if(Tmp < A[j - Increment])A[j] = A[j - Increment];elsebreak;A[j] = Tmp;}
}![]()
希尔排序的最坏情形分析
虽然希尔排序编程简单,但是,其运行时间的分析则完全是另外一回事。希尔排序的运行时间依赖于增量序列的选择,而证明可能相当复杂。希尔排序的平均情形分析,除最平凡的一些增量序列外,是一个长期未解决的问题。我们将证明在两个特别的增量序列下最坏情形的精确的界。
定理 7.3 使用希尔增量时希尔排序的最坏情形运行时间为。
证明:证明不仅需要指出最坏情形运行时间的上界,而且还需要指出存在某个输入实际上就花费时间运行。首先通过构造一个坏情形来证明下界。我们先选择
是2的幂。这使得除最后一个增量是1外所有的增量都是偶数。现在,我们给出一个数组Input-Data作为输入,它的偶数位置上有
个同为最大的数,而在奇数位置上有
个同为最小的数(对该证明,第一个位置是位置1)。由于除最后一个增量外所有的增量都是偶数,因此,当我们进行最后一趟排序前,
个最大的元素仍然处在偶数位置上,而
个最小的元素也还是在奇数位置上。于是,在最后一趟排序开始之前第
个最小的数(
)在位置
上。将第
个元素恢复到其正确位置需要在数组中移动
个间隔。这样,仅仅将
个最小的元素放到正确的位置上就至少需要
的工作。举一个例子,图7-5显示一个
时的坏(但不是最坏)的输入。在2-排序后的逆序数一直恰好保持为1+2+3+4+5+6+7=28,因此,最后一趟排序将花费相当多的时间。
现在我们证明上界以结束本证明。前面已经观察到,带有增量
的一趟排序由
个关于
个元素的插入排序组成。由于插入排序是二次的,因此一趟排序总的开销是
。对所有各趟排序求和则给出总的界为
。因为这些增量形成一个几何级数,其公比为2,而该级数中的最大项是
,因此,
。于是,我们得到总的界
。

希尔增量的问题在于,这些增量对未必互素,因此较小的增量可能影响很小。Hibbard提出一个稍微不同的增量序列,它在实践中(并且理论上)给出更好的结果。他的增量形如。虽然这些增量几乎是相同的,但关键的区别是相邻的增量没有公因子。现在我们就来分析使用这个增量序列的希尔排序的最坏情形运行时间,这个证明相当复杂。
定理 7.4 使用Hibbard增量的希尔排序的最坏情形运行时间为。
证明:我们只证明上界而将下界的证明留作练习。这个证明需要堆垒数论(additivenumber theory)中某些众所周知的结果。本章末提供了这些结果的参考资料。
和前面一样,对于上界,我们还是计算每一趟排序的运行时间的界,然后对各趟求和。对于那些的增量,我们将使用前一定理得到的界
。虽然这个界对于其他增量也是成立的,但是它太大,用不上。直观地看,我们必须利用这个增量序列是特殊的这样一个事实。我们需要证明的是,对于位置
上的任意元素
,当要执行
-排序时,只有少数元素在位置
的左边且大于
。
当对输入数组进行-排序时,我们知道它已经是
-排序和
-排序的了。在
-排序以前,考虑位置
和
上的两个元素,其中
。如果
是
或
的倍数,那么显然
。不仅如此,如果
可以表示为
和
的线性组合(以非负整数的形式),那么也有
。例如,当我们进行3-排序时,文件已经是7-排序和
15-排序的了。52可以表示为7和15的线性组合:52=1×7+3×15。因此,A[100]不可能大于A[152],因为。
现在,,因此
和
没有公因子。在这种情形下,可以证明,至少和
一样大的所有整数都可以表示为
和
的线性组合(见本章末尾的参考文献)。
这就告诉我们,第4行的for循环体对于这些位置上的每一个,最多执行
次。于是我们得到每趟的界
。
利用大约一半的增量满足的事实并假设
是偶数,那么总的运行时间为
因为两个和都是几何级数,并且,所以上式简化为
使用Hibbard增量的希尔排序平均情形运行时间基于模拟的结果被认为是,但是没有人能够证明该结果。Pratt已经证明,
的界适用于广泛的增量序列。
Sedgewick 提出了几种增量序列,其最坏情形运行时间(也是可以达到的)为。对于这些增量序列的平均运行时间猜测为
。经验研究指出,在实践中这些序列的运行要比Hibbard的好得多,其中最好的是序列(1,5,19,41,109,...),该序列中的项或者是
,或者是
。通过将这些值放到一个数组中可以最容易地实现该算法。虽然有可能存在某个增量序列使得能够对希尔排序的运行时间做出重大改进,但是,这个增量在实践中还是最为人们称道的。
关于希尔排序还有几个其他结果,它们需要数论和组合数学中一些艰深的定理而且主要是在理论上有用。希尔排序是算法非常简单又具有极其复杂的分析的一个好例子。
希尔排序的性能在实践中是完全可以接受的,即使是对于数以万计的仍是如此。编程的简单特点使得它成为对较大的输入数据经常选用的算法。
7.5 堆排序
7.6 归并排序
7.7 快速排序
7.7.1 选取枢纽元
7.7.2 分割策略
7.7.3 小数组
7.7.4 实际的快速排序例程
7.7.5 快速排序的分析
7.7.6 选择的线性期望时间算法
7.8 大型结构的排序
7.9 排序的一般下界
7.10 桶式排序
7.11 外部排序
7.11.1 为什么需要新的算法
7.11.2 外部排序模型
7.11.3 简单算法
7.11.4 多路合并
7.11.5 多相合并
7.11.6 替换选择
相关文章:
第7章 排序
前言 在这一章,我们讨论数组元素的排序问题。为简单起见,假设在我们的例子中数组只包含整数,虽然更复杂的结构显然也是可能的。对于本章的大部分内容,我们还假设整个排序工作能够在主存中完成,因此,元素的个…...
AR眼镜光学方案_AR眼镜整机硬件定制
增强现实(Augmented Reality,AR)技术通过将计算机生成的虚拟物体或其他信息叠加到真实世界中,实现对现实的增强。AR眼镜作为实现AR技术的重要设备,具备虚实结合、实时交互的特点。为了实现透视效果,AR眼镜需要同时显示真实的外部世…...
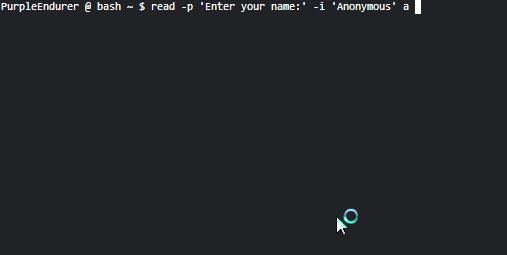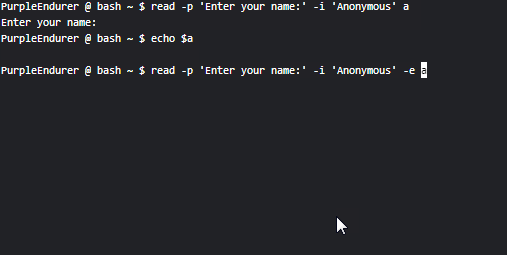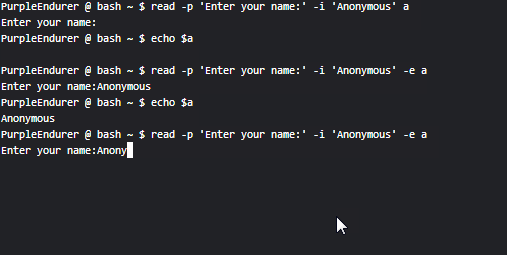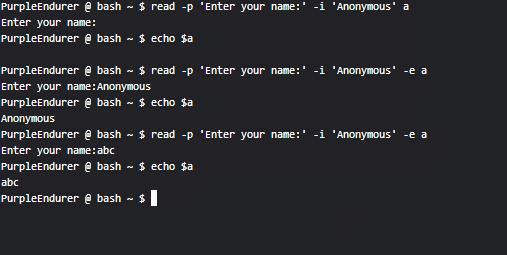
Linux shell编程学习笔记36:read命令
*更新日志 *2023-12-18 1.根据[美] 威廉肖特斯 (Willian shotts)所著《Linux命令行大全(第2版)》 更新了-e、-i、-r选项的说明 2.更新了 2.8 的实例,增加了gif动图 3.补充了-i的应用实例 2.1…...

Python表达式
表达式 本章将解释 Python 中组成表达式的各种元素的的含义。 语法注释: 在本章和后续章节中,会使用扩展 BNF 标注来描述语法而不是词法分析。 当(某种替代的)语法规则具有如下形式 name :: othername并且没有给出语义,则这种…...
风速预测(六)基于Pytorch的EMD-CNN-GRU并行模型
目录 前言 1 风速数据EMD分解与可视化 1.1 导入数据 1.2 EMD分解 2 数据集制作与预处理 2.1 先划分数据集,按照8:2划分训练集和测试集 2.2 设置滑动窗口大小为96,制作数据集 3 基于Pytorch的EMD-CNN-GRU并行模型预测 3.1 数据加载&a…...

【Stm32-F407】全速DAP仿真器下载程序
文章内容如下: 1) 全速DAP仿真器简介2) 全速DAP仿真器下载程序流程 1) 全速DAP仿真器简介 1)全速DAP仿真器简介 DAP全称 Data Acquisition Processor,是一种用于数据采集和实时控制的设备。本文使用的全速DAP仿真器遵循ARM公司的CMSIS-DAP标准ÿ…...

ArcGIS Pro SDK导出的几何XML和Json
本博主会持续更新关于ArcGIS Pro SDK的相关内容,请读者关注一下 圆 XML <PolygonN xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance" xmlns:xs"http://www.w3.org/2001/XMLSchema" xmlns:typens"http://www.esri.com/schemas/…...
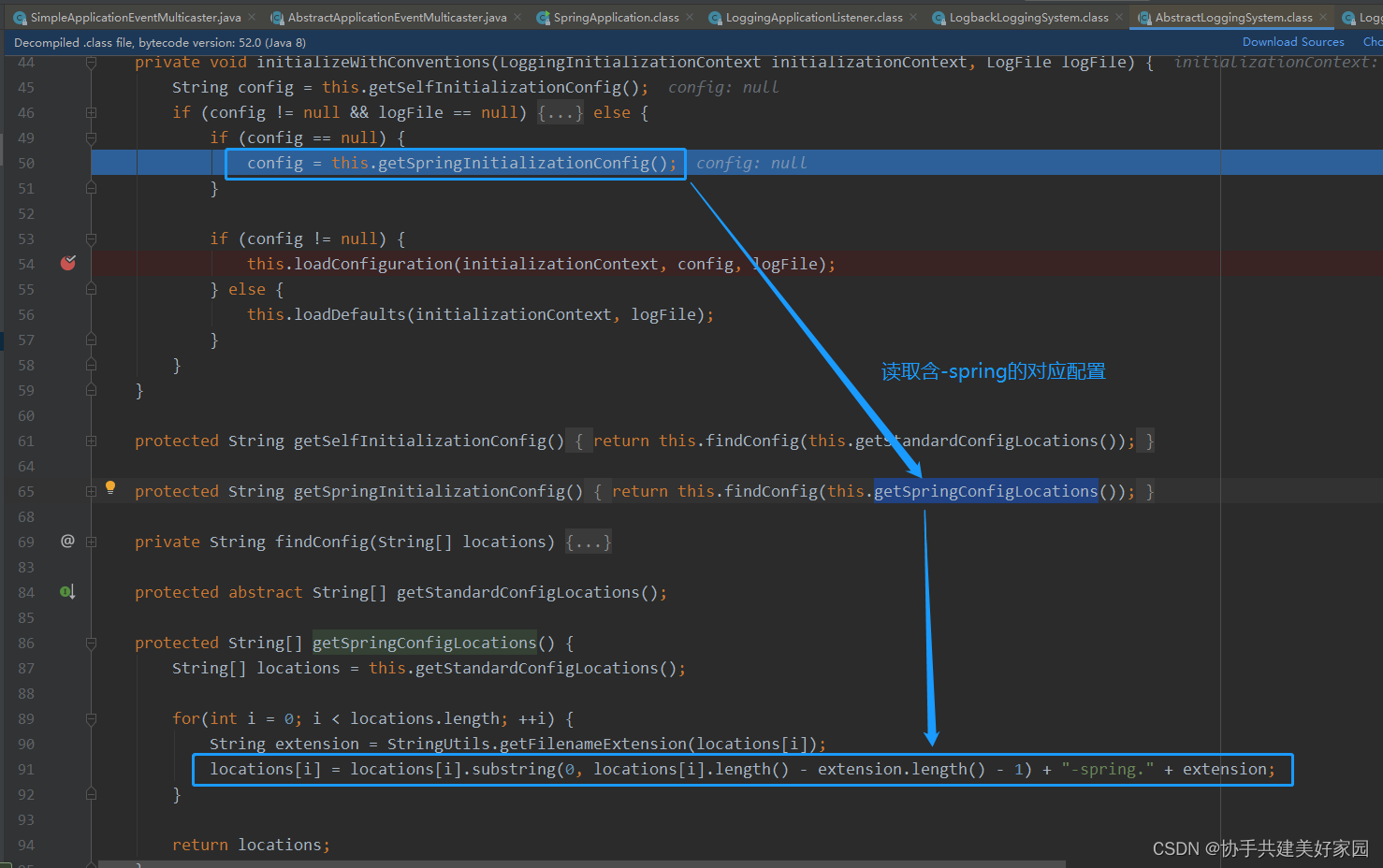
随笔记录-springboot_LoggingApplicationListener+LogbackLoggingSystem
环境:springboot-2.3.1 加载日志监听器初始化日志框架 SpringApplication#prepareEnvironment SpringApplicationRunListeners#environmentPrepared EventPublishingRunListener#environmentPrepared SimpleApplicationEventMulticaster#multicastEvent(Applicati…...

超级计算机与天气预报:精准预测的科技革命
超级计算机与天气预报:精准预测的科技革命 一、引言 随着科技的飞速发展,超级计算机已经成为现代社会不可或缺的一部分。它们在科研、工业、军事等领域发挥着重要作用,其中天气预报是一个颇具代表性的应用领域。本文将探讨超级计算机在天气…...

【uniapp小程序-分享】
//分享到聊天onShareAppMessage() {let shareMessage {title: this.liveInfo.wx_title,path: /subPages/livePages/liveCourse/live_course_info?courseid this.courseid,imageUrl: this.liveInfo.wx_thumb};let shearMsg uni.getStorageSync(shearImg this.courseid);if (…...

思幻二次元风格的工作室个人引导页源码
思幻工作室个人引导页源码已经完成开发!该源码支持三端自适应,并且具备赞助功能。我们选择了当前点赞量最高的配色方案,打造了一个独特的二次元风格引导页。经过在美国服务器上进行的测试,效果令人满意,网页加载速度达…...

Rsync+notify文件实时同步工具
rsync ( Remote sync,远程同步) 是一个开源的快速备份工具,可以在不同主机之间镜像同步整个目录树,支持增量备份,并保持链接和权限,且采用优化的同步算法,传输前执行压缩,因此非常适用于异地备…...
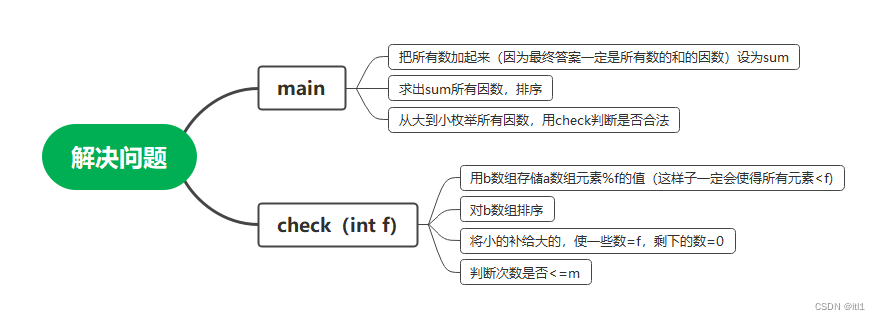
小信砍柴的题解
目录 原题描述: 时间:1s 空间:256M 题目描述: 输入格式: 输出格式: 样例1输入: 题目大意: 主要思路: 注意事项: 总代码: 原题描述&#…...
)
华为OD机试 - 跳格子3(Java JS Python C)
题目描述 小明和朋友们一起玩跳格子游戏, 每个格子上有特定的分数 score = [1, -1, -6, 7, -17, 7], 从起点score[0]开始,每次最大的步长为k,请你返回小明跳到终点 score[n-1] 时,能得到的最大得分。 输入描述 第一行输入总的格子数量 n 第二行输入每个格子的分数 sc…...
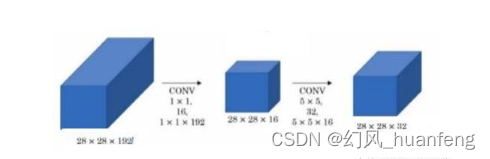
每天五分钟计算机视觉:谷歌的Inception模块的计算成本的问题
计算成本 Inception 层还有一个问题,就是计算成本的问题,我们来看一下55 过滤器在该模块中的计算成本。 原始图片为28*28*192经过32个5*5的过滤操作,它的计算成本为: 我们输出28*28*32个数字,对于输出的每个数字来说,你都需要执行 55192 (5*5为卷积核的大小,192为通道…...
最新AI创作系统ChatGPT系统源码+DALL-E3文生图+支持AI绘画+GPT语音对话功能
一、AI创作系统 SparkAi创作系统是基于ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI…...

78-C语言-完数的判断,以及输出其因子
简介:一个数如果恰好等于它的因子之和,这个数就称为完数,C语言编程找出1000之内的所有完数,并输出其因子。因子可以整除该数字的数, 如6的因子:1 2 3,6%10 6%20 6%30 解释全在注…...
C# 使用FluentHttpClient请求WebApi
写在前面 FluentHttpClient 是一个REST API 异步调用 HTTP 客户端,调用过程非常便捷,采用流式编程,可以将所有请求所需的参数一次性发送,并直接获取序列化后的结果。 老规矩从NuGet上安装该类库: 这边一定要认准是 P…...

AXure交互及案列
AXure交互及案列 1.交互样式简介2.axure交互事件简介3.axure交互动作简介4.axure情形简介2.完成案列1.登录案列2.省市联动案列3.左侧联动 1.交互样式简介 Axure是一种强大的原型设计工具,它允许用户创建高保真的交互式原型,用于演示和测试Web和移动应用…...

美颜SDK技术对比,深入了解视频美颜SDK的工作机制
如何在实时视频中呈现更加自然、美丽的画面,而这正是美颜SDK技术发挥作用的领域之一。本文将对几种主流视频美颜SDK进行深入比较,以揭示它们的工作机制及各自的优劣之处。 随着科技的不断进步,美颜技术已经从简单的图片处理发展到了视频领域…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...
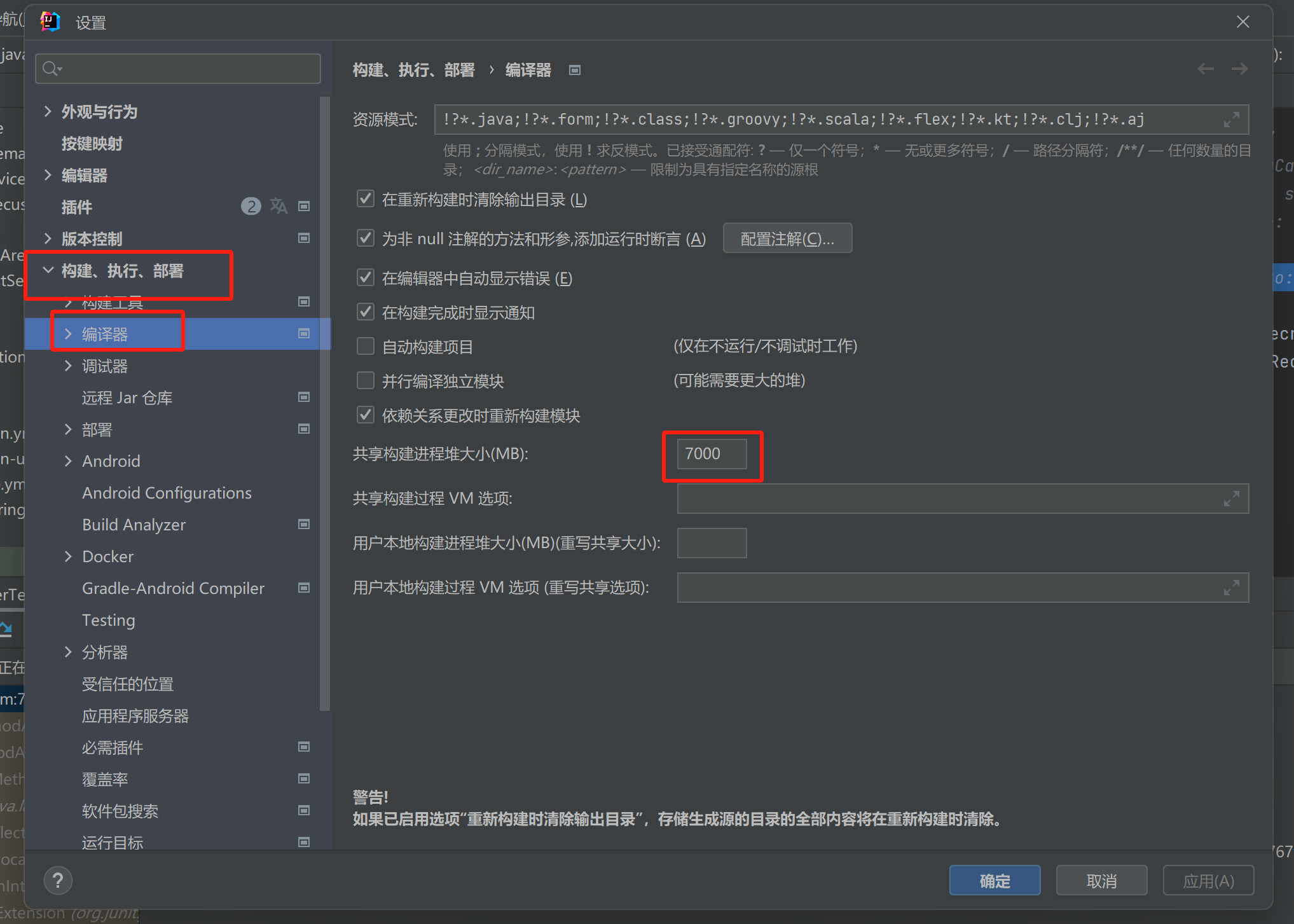
【记录坑点问题】IDEA运行:maven-resources-production:XX: OOM: Java heap space
问题:IDEA出现maven-resources-production:operation-service: java.lang.OutOfMemoryError: Java heap space 解决方案:将编译的堆内存增加一点 位置:设置setting-》构建菜单build-》编译器Complier...
