Python 全栈体系【四阶】(七)
第四章 机器学习
六、多项式回归
1. 什么是多项式回归
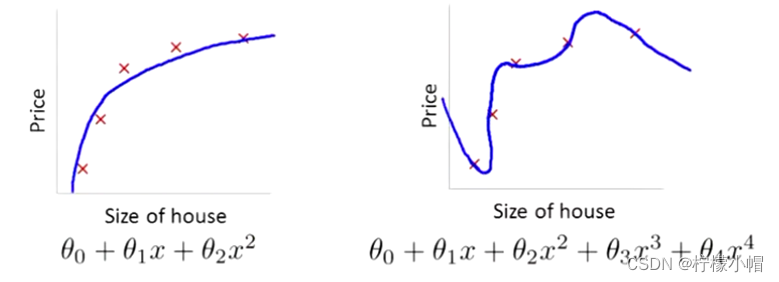
线性回归适用于数据呈线性分布的回归问题。如果数据样本呈明显非线性分布,线性回归模型就不再适用(下图左),而采用多项式回归可能更好(下图右)。例如:
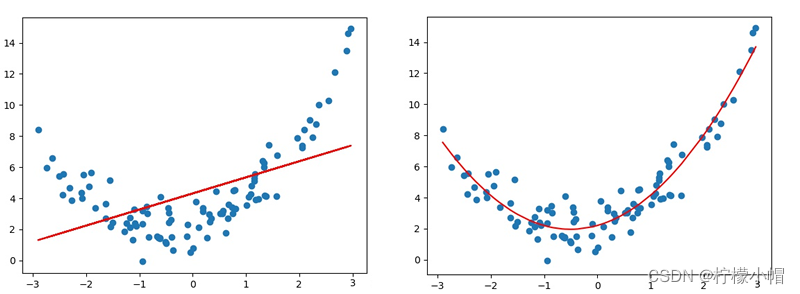
2. 多项式模型定义
与线性模型相比,多项式模型引入了高次项,自变量的指数大于 1,例如一元二次方程:
y = w 0 + w 1 x + w 2 x 2 y = w_0 + w_1x + w_2x^2 y=w0+w1x+w2x2
一元三次方程:
y = w 0 + w 1 x + w 2 x 2 + w 3 x 3 y = w_0 + w_1x + w_2x^2 + w_3x ^ 3 y=w0+w1x+w2x2+w3x3
推广到一元 n 次方程:
y = w 0 + w 1 x + w 2 x 2 + w 3 x 3 + . . . + w n x n y = w_0 + w_1x + w_2x^2 + w_3x ^ 3 + ... + w_nx^n y=w0+w1x+w2x2+w3x3+...+wnxn
上述表达式可以简化为:
y = ∑ i = 1 N w i x i y = \sum_{i=1}^N w_ix^i y=i=1∑Nwixi
3. 与线性回归的关系
多项式回归可以理解为线性回归的扩展,在线性回归模型中添加了新的特征值。例如,要预测一栋房屋的价格,有 x 1 , x 2 , x 3 x_1, x_2, x_3 x1,x2,x3三个特征值,分别表示房子长、宽、高,则房屋价格可表示为以下线性模型:
y = w 1 x 1 + w 2 x 2 + w 3 x 3 + b y = w_1 x_1 + w_2 x_2 + w_3 x_3 + b y=w1x1+w2x2+w3x3+b
对于房屋价格,也可以用房屋的体积,而不直接使用 x 1 , x 2 , x 3 x_1, x_2, x_3 x1,x2,x3三个特征:
y = w 0 + w 1 x + w 2 x 2 + w 3 x 3 y = w_0 + w_1x + w_2x^2 + w_3x ^ 3 y=w0+w1x+w2x2+w3x3
相当于创造了新的特征 x , x x, x x,x = 长 _ 宽 _ 高。
以上两个模型可以解释为:
房屋价格是关于长、宽、高三个特征的线性模型
房屋价格是关于体积的多项式模型
因此,可以将一元 n 次多项式变换成 n 元一次线性模型。
4. 多项式回归实现
对于一元 n 次多项式,同样可以利用梯度下降对损失值最小化的方法,寻找最优的模型参数 w 0 , w 1 , w 2 , . . . , w n w_0, w_1, w_2, ..., w_n w0,w1,w2,...,wn。可以将一元 n 次多项式,变换成 n 元一次多项式,求线性回归。以下是一个多项式回归的实现。
# 多项式回归示例
import numpy as np
# 线性模型
import sklearn.linear_model as lm
# 模型性能评价模块
import sklearn.metrics as sm
import matplotlib.pyplot as mp
# 管线模块
import sklearn.pipeline as pl
import sklearn.preprocessing as sptrain_x, train_y = [], [] # 输入、输出样本
with open("poly_sample.txt", "rt") as f:for line in f.readlines():data = [float(substr) for substr in line.split(",")]train_x.append(data[:-1])train_y.append(data[-1])train_x = np.array(train_x) # 二维数据形式的输入矩阵,一行一样本,一列一特征
train_y = np.array(train_y) # 一维数组形式的输出序列,每个元素对应一个输入样本
# print(train_x)
# print(train_y)# 将多项式特征扩展预处理,和一个线性回归器串联为一个管线
# 多项式特征扩展:对现有数据进行的一种转换,通过将数据映射到更高维度的空间中
# 进行多项式扩展后,我们就可以认为,模型由以前的直线变成了曲线
# 从而可以更灵活的去拟合数据
# pipeline连接两个模型
model = pl.make_pipeline(sp.PolynomialFeatures(3), # 多项式特征扩展,扩展最高次项为3lm.LinearRegression())# 用已知输入、输出数据集训练回归器
model.fit(train_x, train_y)
# print(model[1].coef_)
# print(model[1].intercept_)# 根据训练模型预测输出
pred_train_y = model.predict(train_x)# 评估指标
err4 = sm.r2_score(train_y, pred_train_y) # R2得分, 范围[0, 1], 分值越大越好
print(err4)# 在训练集之外构建测试集
test_x = np.linspace(train_x.min(), train_x.max(), 1000)
pre_test_y = model.predict(test_x.reshape(-1, 1)) # 对新样本进行预测# 可视化回归曲线
mp.figure('Polynomial Regression', facecolor='lightgray')
mp.title('Polynomial Regression', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.scatter(train_x, train_y, c='dodgerblue', alpha=0.8, s=60, label='Sample')mp.plot(test_x, pre_test_y, c='orangered', label='Regression')mp.legend()
mp.show()
打印输出:
0.9224401504764776
执行结果:
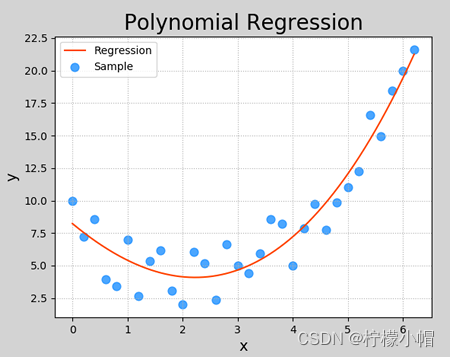
5. 过拟合与欠拟合
5.1 什么是欠拟合、过拟合
在上一小节多项式回归示例中,多项特征扩展器 PolynomialFeatures()进行多项式扩展时,指定了最高次数为 3,该参数为多项式扩展的重要参数,如果选取不当,则可能导致不同的拟合效果。下图显示了该参数分别设为 1、20 时模型的拟合图像:
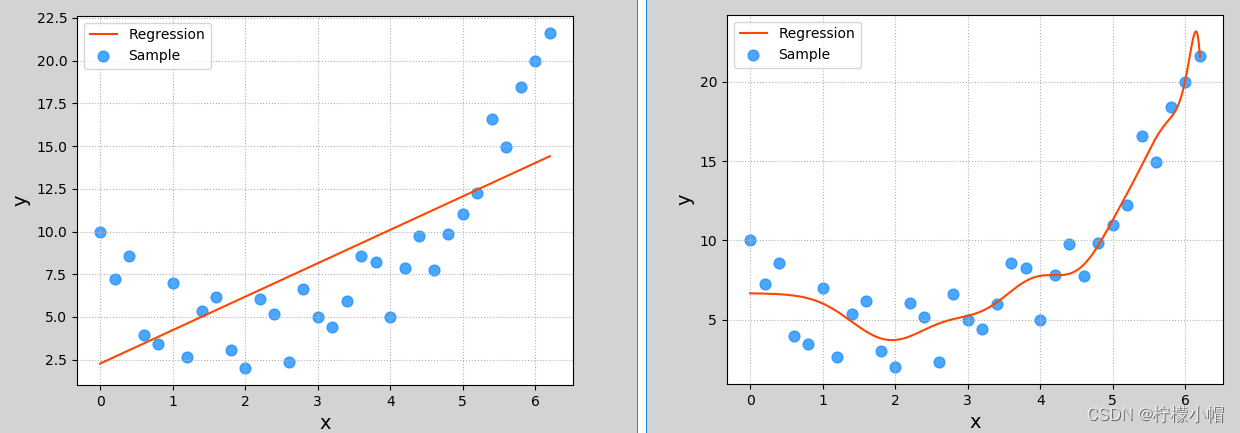
这两种其实都不是好的模型。前者没有学习到数据分布规律,模型拟合程度不够,预测准确度过低,这种现象称为“欠拟合”;后者过于拟合更多样本,以致模型泛化能力(新样本的适应性)变差,这种现象称为“过拟合”。欠拟合模型一般表现为训练集、测试集下准确度都比较低;过拟合模型一般表现为训练集下准确度较高、测试集下准确度较低。 一个好的模型,不论是对于训练数据还是测试数据,都有接近的预测精度,而且精度不能太低。
【思考 1】以下哪种模型较好,哪种模型较差,较差的原因是什么?
| 训练集 R2 值 | 测试集 R2 值 |
|---|---|
| 0.6 | 0.5 |
| 0.9 | 0.6 |
| 0.9 | 0.88 |
【答案】第一个模型欠拟合;第二个模型过拟合;第三个模型适中,为可接受的模型。
【思考 2】以下哪个曲线为欠拟合、过拟合,哪个模型拟合最好?
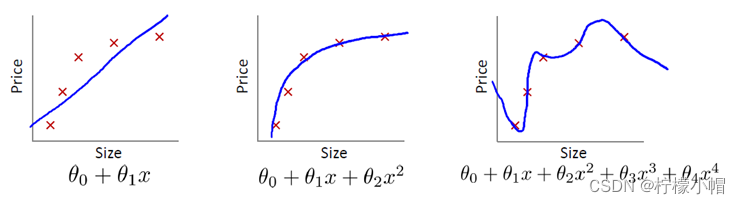
【答案】第一个模型欠拟合;第三个模型过拟合;第二个模型拟合较好。
5.2 如何处理欠拟合、过拟合
欠拟合:提高模型复杂度,如增加特征、增加模型最高次幂等等;
过拟合:降低模型复杂度,如减少特征、降低模型最高次幂等等。
七、线性回归模型变种
1. 正则化
1.1 什么是正则化
过拟合还有一个常见的原因,就是模型参数值太大,所以可以通过抑制参数的方式来解决过拟合问题。如下图所示,右图产生了一定程度过拟合,可以通过弱化高次项的系数(但不删除)来降低过拟合。
例如,可以通过在 θ 3 , θ 4 \theta_3, \theta_4 θ3,θ4的系数上添加一定的系数,来压制这两个高次项的系数,这种方法称为正则化。但在实际问题中,可能有更多的系数,我们并不知道应该压制哪些系数,所以,可以通过收缩所有系数来避免过拟合。
1.2 正则化的定义
正则化是指,在目标函数后面添加一个范数,来防止过拟合的手段,这个范数定义为:
∣ ∣ x ∣ ∣ p = ( ∑ i = 1 N ∣ x ∣ p ) 1 p ||x||_p = (\sum_{i=1}^N |x|^p)^{\frac{1}{p}} ∣∣x∣∣p=(i=1∑N∣x∣p)p1
当 p=1 时,称为 L1 范数(即所有系数绝对值之和):
∣ ∣ x ∣ ∣ 1 = ( ∑ i = 1 N ∣ x ∣ ) ||x||_1 = (\sum_{i=1}^N |x|) ∣∣x∣∣1=(i=1∑N∣x∣)
当 p=2 是,称为 L2 范数(即所有系数平方之和再开方):
∣ ∣ x ∣ ∣ 2 = ( ∑ i = 1 N ∣ x ∣ 2 ) 1 2 ||x||_2 = (\sum_{i=1}^N |x|^2)^{\frac{1}{2}} ∣∣x∣∣2=(i=1∑N∣x∣2)21
通过对目标函数添加正则项,整体上压缩了参数的大小,从而防止过拟合。
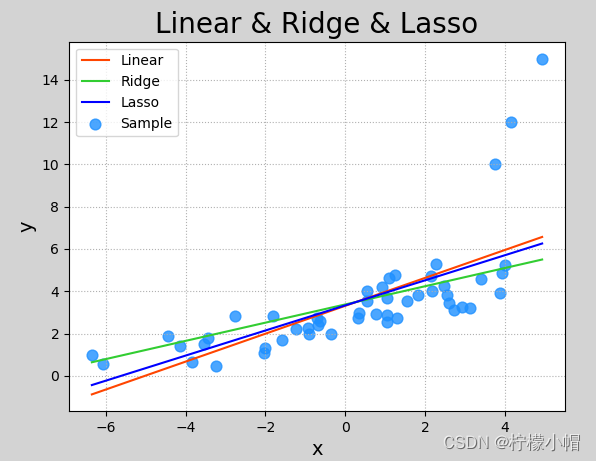
2. Lasso 回归与岭回归
Lasso 回归和岭回归(Ridge Regression)都是在标准线性回归的基础上修改了损失函数的回归算法。 Lasso 回归全称为 Least absolute shrinkage and selection operator,又译“最小绝对值收敛和选择算子”、”套索算法”,其损失函数如下所示:
E = 1 n ( ∑ i = 1 N y i − y i ′ ) 2 + λ ∣ ∣ w ∣ ∣ 1 E = \frac{1}{n}(\sum_{i=1}^N y_i - y_i')^2 + \lambda ||w||_1 E=n1(i=1∑Nyi−yi′)2+λ∣∣w∣∣1
岭回归损失函数为:
E = 1 n ( ∑ i = 1 N y i − y i ′ ) 2 + λ ∣ ∣ w ∣ ∣ 2 E = \frac{1}{n}(\sum_{i=1}^N y_i - y_i')^2 + \lambda ||w||_2 E=n1(i=1∑Nyi−yi′)2+λ∣∣w∣∣2
从逻辑上说,Lasso 回归和岭回归都可以理解为通过调整损失函数,减小函数的系数,从而避免过于拟合于样本,降低偏差较大的样本的权重和对模型的影响程度。
线性模型变种模型:在损失函数后面 + 正则项
- 损失函数 + L1 范数 -> Lasso 回归
- 损失函数 + L2 范数 -> 岭回归
以下关于 Lasso 回归于岭回归的 sklearn 实现:
# Lasso回归和岭回归示例
import numpy as np
# 线性模型
import sklearn.linear_model as lm
# 模型性能评价模块
import sklearn.metrics as sm
import matplotlib.pyplot as mpx, y = [], [] # 输入、输出样本
with open("abnormal.txt", "rt") as f:for line in f.readlines():data = [float(substr) for substr in line.split(",")]x.append(data[:-1])y.append(data[-1])x = np.array(x) # 二维数据形式的输入矩阵,一行一样本,一列一特征
y = np.array(y) # 一维数组形式的输出序列,每个元素对应一个输入样本
# print(x)
# print(y)# 创建线性回归器
model = lm.LinearRegression()
# 用已知输入、输出数据集训练回归器
model.fit(x, y)
# 根据训练模型预测输出
pred_y = model.predict(x)# 创建岭回归器并进行训练
# Ridge: 第一个参数为正则强度,该值越大,异常样本权重就越小
model_2 = lm.Ridge(alpha=200, max_iter=1000) # 创建对象, max_iter为最大迭代次数
model_2.fit(x, y) # 训练
pred_y2 = model_2.predict(x) # 预测# lasso回归
model_3 = lm.Lasso(alpha=0.5, # L1范数相乘的系数max_iter=1000) # 最大迭代次数
model_3.fit(x, y) # 训练
pred_y3 = model_3.predict(x) # 预测# 可视化回归曲线
mp.figure('Linear & Ridge & Lasso', facecolor='lightgray')
mp.title('Linear & Ridge & Lasso', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.scatter(x, y, c='dodgerblue', alpha=0.8, s=60, label='Sample')
sorted_idx = x.T[0].argsort()mp.plot(x[sorted_idx], pred_y[sorted_idx], c='orangered', label='Linear') # 线性回归
mp.plot(x[sorted_idx], pred_y2[sorted_idx], c='limegreen', label='Ridge') # 岭回归
mp.plot(x[sorted_idx], pred_y3[sorted_idx], c='blue', label='Lasso') # Lasso回归mp.legend()
mp.show()
以下是执行结果:
八、模型保存与加载
可以使用 Python 提供的功能对模型对象进行保存。使用方法如下:
import pickle
# 保存模型
pickle.dump(模型对象, 文件对象)
# 加载模型
model_obj = pickle.load(文件对象)
保存训练模型应该在训练完成或评估完成之后,完整代码如下:
# 模型保存示例
import numpy as np
import sklearn.linear_model as lm # 线性模型
import picklex = np.array([[0.5], [0.6], [0.8], [1.1], [1.4]]) # 输入集
y = np.array([5.0, 5.5, 6.0, 6.8, 7.0]) # 输出集# 创建线性回归器
model = lm.LinearRegression()
# 用已知输入、输出数据集训练回归器
model.fit(x, y)print("训练完成.")# 保存训练后的模型
with open('linear_model.pkl', 'wb') as f:pickle.dump(model, f)print("保存模型完成.")
执行完成后,可以看到与源码相同目录下多了一个名称为 linear_model.pkl 的文件,这就是保存的训练模型。使用该模型代码:
# 模型加载示例
import numpy as np
import sklearn.linear_model as lm # 线性模型
import sklearn.metrics as sm # 模型性能评价模块
import matplotlib.pyplot as mp
import picklex = np.array([[0.5], [0.6], [0.8], [1.1], [1.4]]) # 输入集
y = np.array([5.0, 5.5, 6.0, 6.8, 7.0]) # 输出集# 加载模型
with open('linear_model.pkl', 'rb') as f:model = pickle.load(f)print("加载模型完成.")# 根据加载的模型预测输出
pred_y = model.predict(x)# 可视化回归曲线
mp.figure('Linear Regression', facecolor='lightgray')
mp.title('Linear Regression', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.scatter(x, y, c='blue', alpha=0.8, s=60, label='Sample')mp.plot(x, pred_y, c='orangered', label='Regression')mp.legend()
mp.show()
执行结果和训练模型预测结果一样。
九、总结
1. 什么是线性模型
线性模型是自然界最简单的模型之一,反映自变量、因变量之间的等比例增长关系。
2. 什么时候使用线性回归
线性模型只能用于满足线性分布规律的数据中。
3. 如何实现线性回归
给定一组样本,给定初始的 w 和 b,通过梯度下降法求最优的 w 和 b。
十、补充知识
1. R2 系数详细计算
R2 系数详细计算过程如下:
若用 y i y_i yi表示真实的观测值,用 y ˉ \bar{y} yˉ表示真实观测值的平均值,用 y i ^ \hat{y_i} yi^表示预测值,则有以下评估指标:
回归平方和(SSR)
S S R = ∑ i = 1 n ( y i ^ − y ˉ ) 2 SSR = \sum_{i=1}^{n}(\hat{y_i} - \bar{y})^2 SSR=i=1∑n(yi^−yˉ)2
- 估计值与平均值的误差,反映自变量与因变量之间的相关程度的偏差平方和。
残差平方和(SSE)
S S E = ∑ i = 1 n ( y i − y i ^ ) 2 SSE = \sum_{i=1}^{n}(y_i-\hat{y_i} )^2 SSE=i=1∑n(yi−yi^)2
- 即估计值与真实值的误差,反映模型拟合程度。
总离差平方和(SST)
S S T = S S R + S S E = ∑ i = 1 n ( y i − y ˉ ) 2 SST =SSR + SSE= \sum_{i=1}^{n}(y_i - \bar{y})^2 SST=SSR+SSE=i=1∑n(yi−yˉ)2
- 即平均值与真实值的误差,反映与数学期望的偏离程度.
R2_score 计算公式
R2_score,即决定系数,反映因变量的全部变异能通过回归关系被自变量解释的比例。计算公式:
R 2 = 1 − S S E S S T R^2=1-\frac{SSE}{SST} R2=1−SSTSSE
即:
R 2 = 1 − ∑ i = 1 n ( y i − y ^ i ) 2 ∑ i = 1 n ( y i − y ˉ ) 2 R^2 = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)2}{\sum_{i=1}{n} (y_i - \bar{y})^2} R2=1−∑i=1n(yi−yˉ)2∑i=1n(yi−y^i)2
进一步化简为:
R 2 = 1 − ∑ i ( y i − y i ) 2 / n ∑ i ( y i − y ^ ) 2 / n = 1 − R M S E V a r R^2 = 1 - \frac{\sum\limits_i(y_i - y_i)^2 / n}{\sum\limits_i(y_i - \hat{y})^2 / n} = 1 - \frac{RMSE}{Var} R2=1−i∑(yi−y^)2/ni∑(yi−yi)2/n=1−VarRMSE
分子就变成了常用的评价指标均方误差 MSE,分母就变成了方差,对于 R 2 R^2 R2可以通俗地理解为使用均值作为误差基准,看预测误差是否大于或者小于均值基准误差。
R2_score = 1,样本中预测值和真实值完全相等,没有任何误差,表示回归分析中自变量对因变量的解释越好。
R2_score = 0,此时分子等于分母,样本的每项预测值都等于均值。
2. 线性回归损失函数求导过程
线性函数定义为:
y = w 0 + w 0 x 1 y = w_0 + w_0 x_1 y=w0+w0x1
采用均方差损失函数:
l o s s = 1 2 ( y − y ′ ) 2 loss = \frac{1}{2} (y - y')^2 loss=21(y−y′)2
其中,y 为真实值,来自样本;y’为预测值,即线性方程表达式,带入损失函数得:
l o s s = 1 2 ( y − ( w 0 + w 1 x 1 ) ) 2 loss = \frac{1}{2} (y - (w_0 + w_1 x_1))^2 loss=21(y−(w0+w1x1))2
将该式子展开:
l o s s = 1 2 ( y 2 − 2 y ( w 0 + w 1 x 1 ) + ( w 0 + w 1 x 1 ) 2 ) = 1 2 ( y 2 − 2 y ∗ w 0 − 2 y ∗ w 1 x 1 + w 0 2 + 2 w 0 ∗ w 1 x 1 + w 1 2 x 1 2 ) loss = \frac{1}{2} (y^2 - 2y(w_0 + w_1 x_1) + (w_0 + w_1 x_1)^2) =\\\frac{1}{2} (y^2 - 2y*w_0 - 2y*w_1x_1 + w_0^2 + 2w_0*w_1 x_1 + w_1^2x_1^2) \\ loss=21(y2−2y(w0+w1x1)+(w0+w1x1)2)=21(y2−2y∗w0−2y∗w1x1+w02+2w0∗w1x1+w12x12)
对 w 0 w_0 w0求导:
∂ l o s s ∂ w 0 = 1 2 ( 0 − 2 y − 0 + 2 w 0 + 2 w 1 x 1 + 0 ) = 1 2 ( − 2 y + 2 w 0 + 2 w 1 x 1 ) = 1 2 ∗ 2 ( − y + ( w 0 + w 1 x 1 ) ) = ( − y + y ′ ) = − ( y − y ′ ) \frac{\partial loss}{\partial w_0} = \frac{1}{2}(0-2y-0+2w_0 + 2w_1 x_1 +0) \\=\frac{1}{2}(-2y + 2 w_0 + 2w_1 x_1) \\= \frac{1}{2} * 2(-y + (w_0 + w_1 x_1)) \\=(-y + y') = -(y - y') ∂w0∂loss=21(0−2y−0+2w0+2w1x1+0)=21(−2y+2w0+2w1x1)=21∗2(−y+(w0+w1x1))=(−y+y′)=−(y−y′)
对 w 1 w_1 w1求导:
∂ l o s s ∂ w 1 = 1 2 ( 0 − 0 − 2 y ∗ x 1 + 0 + 2 w 0 x 1 + 2 w 1 x 1 2 ) = 1 2 ( − 2 y x 1 + 2 w 0 x 1 + 2 w 1 x 1 2 ) = 1 2 ∗ 2 x 1 ( − y + w 0 + w 1 x 1 ) = x 1 ( − y + y ′ ) = − x 1 ( y − y ′ ) \frac{\partial loss}{\partial w_1} = \frac{1}{2}(0-0-2y*x_1+0+2 w_0 x_1 + 2 w_1 x_1^2) \\= \frac{1}{2} (-2y x_1 + 2 w_0 x_1 + 2w_1 x_1^2) \\= \frac{1}{2} * 2 x_1(-y + w_0 + w_1 x_1) \\= x_1(-y + y') = - x_1(y - y') ∂w1∂loss=21(0−0−2y∗x1+0+2w0x1+2w1x12)=21(−2yx1+2w0x1+2w1x12)=21∗2x1(−y+w0+w1x1)=x1(−y+y′)=−x1(y−y′)
推导完毕。
相关文章:

Python 全栈体系【四阶】(七)
第四章 机器学习 六、多项式回归 1. 什么是多项式回归 线性回归适用于数据呈线性分布的回归问题。如果数据样本呈明显非线性分布,线性回归模型就不再适用(下图左),而采用多项式回归可能更好(下图右)。例…...

智能优化算法应用:基于蛾群算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于蛾群算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于蛾群算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.蛾群算法4.实验参数设定5.算法结果6.参考文献7.MA…...

Tekton 克隆 git 仓库
Tekton 克隆 git仓库 介绍如何使用 Tektonhub 官方 git-clone task 克隆 github 上的源码到本地。 git-clone task yaml文件下载地址:https://hub.tekton.dev/tekton/task/git-clone 查看git-clone task yaml内容: 点击Install,选择一种…...

高通平台开发系列讲解(AI篇)SNPE工作流程介绍
文章目录 一、转换网络模型二、量化2.1、选择量化或非量化模型2.2、使用离线TensorFlow或Caffe模型2.3、使用非量化DLC初始化SNPE2.4、使用量化DLC初始化SNPE三、准备输入数据四、运行加载网络沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇章主要介绍SNPE模型工作…...

YoloV8改进策略:ASF-YOLO,结合了空间和尺度特征在小目标和密集目标场景有效涨点
摘要 本文提出了一种新型的Attentional Scale Sequence Fusion based You Only Look Once (YOLO)框架(ASF-YOLO),该框架结合了空间和尺度特征,以实现准确且快速的细胞实例分割。该框架建立在YOLO分割框架之上,采用Scale Sequence Feature Fusion (SSFF)模块增强网络的多尺…...
OpenCV-8RGB和BGR颜色空间
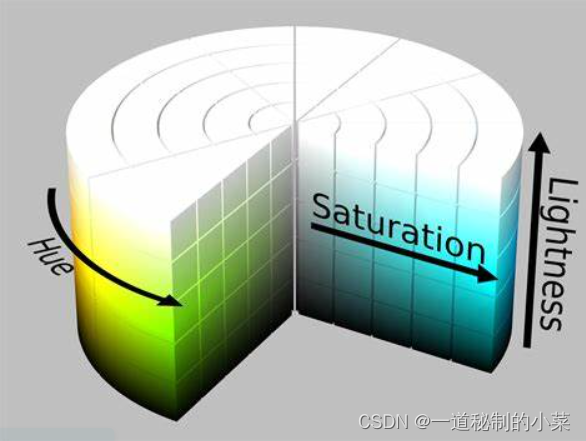
一. RGB和BGR 最常见的色彩空间就是RGB,人眼也是基于RGB的色彩空间去分辨颜色。 OpenCV默认使用的是BGR. BGR和RGB色彩空间的区别在于图片在色彩通道上的排列顺序不同。 二.HSV, HSL和YUV 1.HSV(HSB) OpenCV用的最多的色彩空间是HSV. Hue:色相&…...
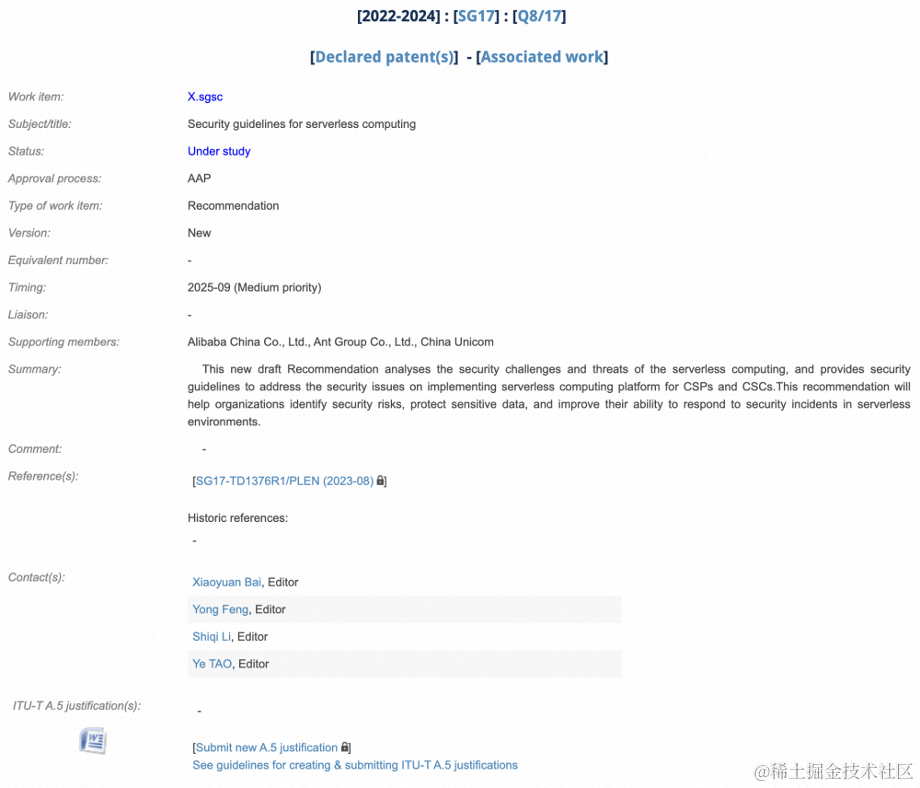
阿里云主导《Serverless 计算安全指南》国际标准正式立项!
日前,在韩国召开的国际电信联盟电信标准分局 ITU-T SG17 全会上,由阿里云主导的《Serverless 计算安全指南》国际标准正式立项成功。 图 1 项目信息 在现今数字化时代,Serverless 计算正逐渐成为云计算的一个新的发展方向,其灵活…...

YOLOv5改进 | 2023 | CARAFE提高精度的上采样方法(助力细节长点)
一、本文介绍 本文给大家带来的CARAFE(Content-Aware ReAssembly of FEatures)是一种用于增强卷积神经网络特征图的上采样方法。其主要旨在改进传统的上采样方法(就是我们的Upsample)的性能。CARAFE的核心思想是:使用…...
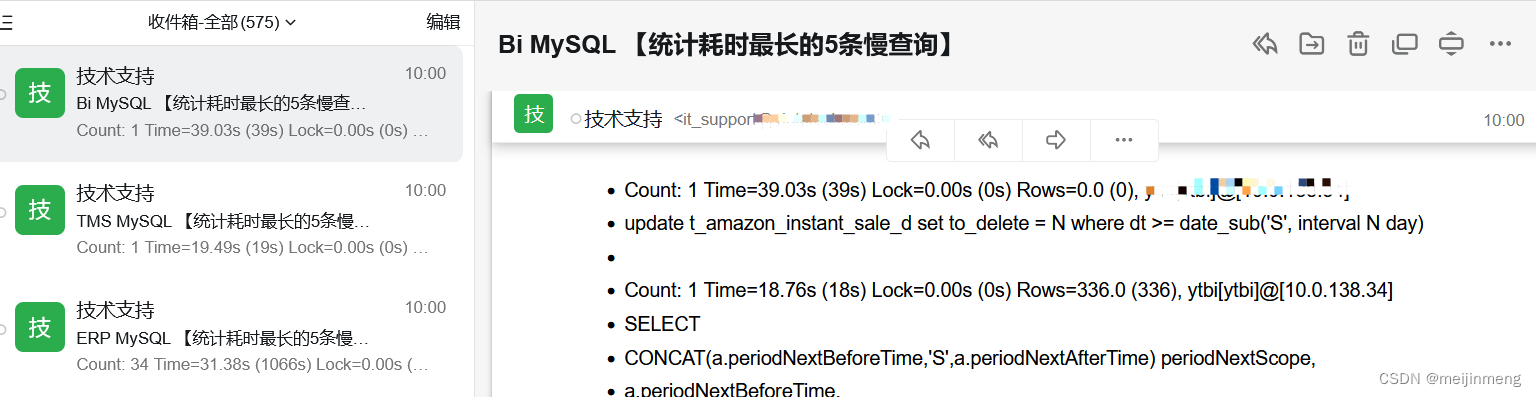
AWS RDS慢日志文件另存到ES并且每天发送邮件统计慢日志
1.背景:需要对aws rds慢日志文件归档到es,让开发能够随时查看。 2.需求:并且每天把最新的慢日志,过滤最慢的5条sql 发送给各个产品线的开发负责人。 3.准备: aws ak/sk ,如果rds 在不同区域需要认证不同的…...

如何在断线后不重连加入音视频房间
RTC 房间断网后,默认是一直尝试重连的,例如当主播再次联网重连成功后,会自动发布之前在发布的音视频流。针对某些不想断网后重新加入连接的场景,需要如下配置: 1、配置断开后不去重连(这种情况也会重连 4 次…...

RabbitMq交换机详解
目录 1.交换机类型2.Fanout交换机2.1.声明队列和交换机2.2.消息发送2.3.消息接收2.4.总结 3.Direct交换机3.1.声明队列和交换机3.2.消息接收3.3.消息发送3.4.总结 4.Topic交换机4.1.说明4.2.消息发送4.3.消息接收4.4.总结 5.Headers交换机5.1.说明5.2.消息发送5.3.消息接收5.4.…...

智能优化算法应用:基于适应度相关算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于适应度相关算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于适应度相关算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.适应度相关算法4.实验参数设定5.算法…...

spring之基于注解管理Bean
学习的最大理由是想摆脱平庸,早一天就多一份人生的精彩;迟一天就多一天平庸的困扰。各位小伙伴,如果您: 想系统/深入学习某技术知识点… 一个人摸索学习很难坚持,想组团高效学习… 想写博客但无从下手,急需…...

Wireshark在云计算中的应用
第一章:Wireshark基础及捕获技巧 1.1 Wireshark基础知识回顾 1.2 高级捕获技巧:过滤器和捕获选项 1.3 Wireshark与其他抓包工具的比较 第二章:网络协议分析 2.1 网络协议分析:TCP、UDP、ICMP等 2.2 高级协议分析:HTTP…...
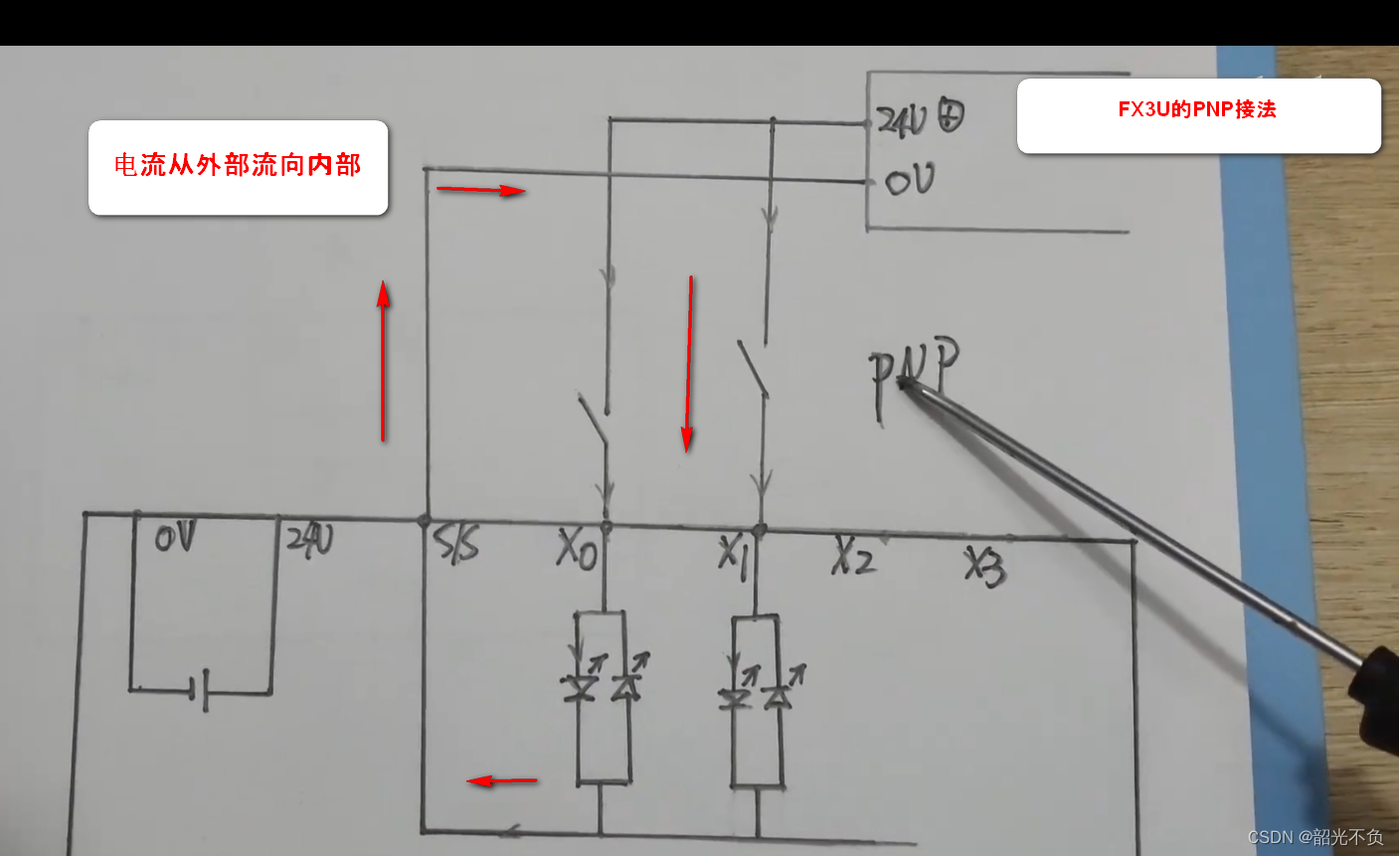
三菱plc学习入门(一,认识三菱plc)
今天就开始对三菱的plc软件入一个门,希望小编的文章对读者和初学者有所帮助!欢迎评论指正,废话不多说,下面开始学习。 目录 plc的型号介绍 M表示什么? T表示什么? R表示什么? 为什么三菱没…...
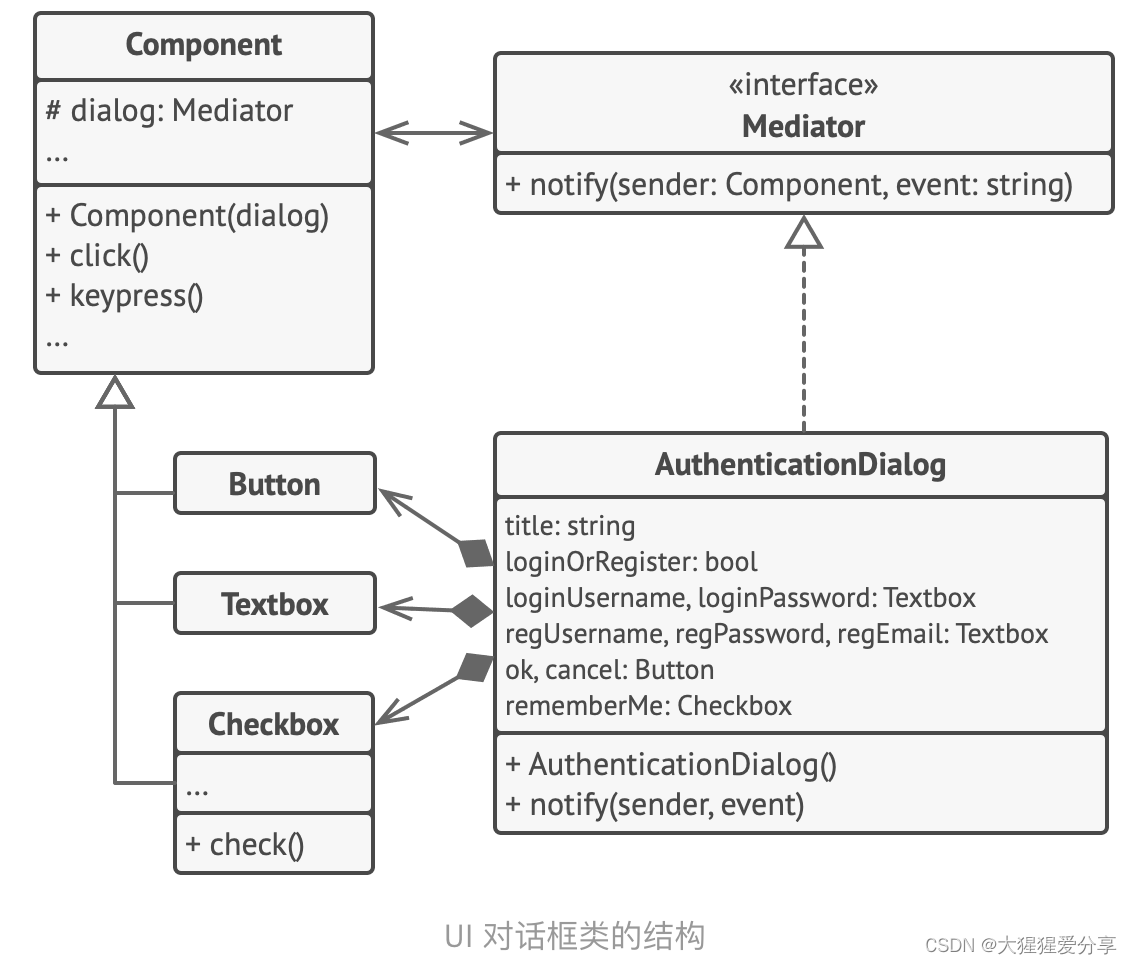
设计模式——中介者模式
引言 中介者模式是一种行为设计模式, 能让你减少对象之间混乱无序的依赖关系。 该模式会限制对象之间的直接交互, 迫使它们通过一个中介者对象进行合作。 问题 假如你有一个创建和修改客户资料的对话框, 它由各种控件组成, 例如…...
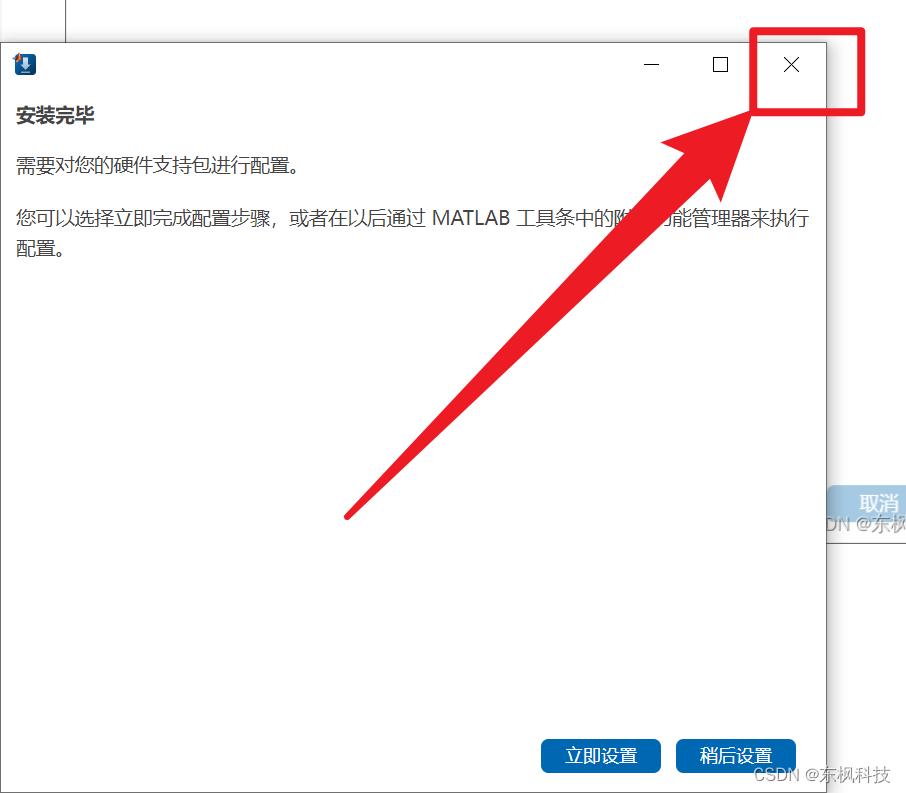
【 USRP安装教程】MATLAB 2023B
步骤 matlabdocusrp驱动包 doc 安装包内容列表 双击“R2023b_Doc_Windows.iso” 打开cmd 查看盘符 切换盘符 因为是F盘,所以cmd输入:“F:” F:进入可安装界面 cd F:\bin\win64安装离线文档库 .\mpm install-doc --matlabroot"C:\MATLAB\R202…...

AI绘画中UNet用于预测噪声
介绍 在AI绘画领域中,UNet是一种常见的神经网络架构,广泛用于图像相关的任务,尤其是在图像分割领域中表现突出。UNet最初是为了解决医学图像分割问题而设计的,但其应用已经扩展到了多种图像处理任务。 特点 对称结构:…...

解决 Hbuilder打包 Apk pad 无法横屏 以及 H5 直接打包 成Apk
解决 Hbuilder打包 Apk pad 无法横屏 前言云打包配置 前言 利用VUE 写了一套H5 想着 做一个APP壳 然后把 H5 直接嵌进去 客户要求 在pad 端 能够操作 然后页面风格 也需要pad 横屏展示 云打包 配置 下面是manifest.json 配置文件 {"platforms": ["iPad"…...

云原生之深入解析如何在K8S环境中使用Prometheus来监控CoreDNS指标
一、什么是 Kubernetes CoreDNS? CoreDNS 是 Kubernetes 环境的DNS add-on 组件,它是在控制平面节点中运行的组件之一,使其正常运行和响应是 Kubernetes 集群正常运行的关键。DNS 是每个体系结构中最敏感和最重要的服务之一。应用程序、微服…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

EEG-fNIRS联合成像在跨频率耦合研究中的创新应用
摘要 神经影像技术对医学科学产生了深远的影响,推动了许多神经系统疾病研究的进展并改善了其诊断方法。在此背景下,基于神经血管耦合现象的多模态神经影像方法,通过融合各自优势来提供有关大脑皮层神经活动的互补信息。在这里,本研…...
【QT控件】显示类控件
目录 一、Label 二、LCD Number 三、ProgressBar 四、Calendar Widget QT专栏:QT_uyeonashi的博客-CSDN博客 一、Label QLabel 可以用来显示文本和图片. 核心属性如下 代码示例: 显示不同格式的文本 1) 在界面上创建三个 QLabel 尺寸放大一些. objectName 分别…...
