Leetcode 1901. 寻找峰值 II(Java + 列最大值 + 二分)
题目
- 1901. 寻找峰值 II
- 一个 2D 网格中的 峰值 是指那些 严格大于 其相邻格子(上、下、左、右)的元
- 给你一个 从 0 开始编号 的 m x n 矩阵 mat ,其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值 mat[i][j] 并 返回其位置 [i,j] 。
- 你可以假设整个矩阵周边环绕着一圈值为 -1 的格子。
- 要求必须写出时间复杂度为 O(m log(n)) 或 O(n log(m)) 的算法
- m == mat.length
- n == mat[i].length
- 1 <= m, n <= 500
- 1 <= mat[i][j] <= 10 ^ 5
- 任意两个相邻元素均不相等.
解法
Java + 列最大值 + 二分
第 1 步:
- 类似:Leetcode 162. 寻找峰值(Java + 二分)
- 在行内找严格大于左右的元素,再找每列的最大值(一定是大于上下)
- 一定需要找该列的最大值,如果这也二分找极大值(仅严格大于左右),那么可能找到非该列最大值从而导致 左/右 列误判
第 2 步:
- 具体做法:
- 先找中间=mid 列,找到俩最大值 mat[maxRow][mid] ,元素一定严格大于上下的元素
- 如果 mat[maxRow][mid] 严格大于左右的元素,则直接返回,否则下一步
- 如果 mat[maxRow][mid] > mat[maxRow][mid+1] 则 maxRow 左边列一定存在,否则 maxRow 右边列一定存在
- 时间复杂度:O(m*logn),空间复杂度:O(1)
代码
/*** Java + 列最大值 + 二分:** 第 1 步:* 类似:162. 寻找峰值 FindPeakElement,在行内找严格大于左右的元素,再找每列的最大值(一定是大于上下)* 一定需要找该列的最大值,如果这也二分找极大值(仅严格大于左右),那么可能找到非该列最大值从而导致 左/右 列误判** 第 2 步:* 具体做法:* * 先找中间=mid 列,找到俩最大值 mat[maxRow][mid] ,元素一定严格大于上下的元素* * 如果 mat[maxRow][mid] 严格大于左右的元素,则直接返回,否则下一步* * 如果 mat[maxRow][mid] > mat[maxRow][mid+1] 则 maxRow 左边列一定存在,否则 maxRow 右边列一定存在* 时间复杂度:O(m*logn),空间复杂度:O(1)***/public int[] findPeakGrid(int[][] mat) {int leftCol = 0;int rightCol = mat[0].length - 1;int resCol = 0;while (leftCol <= rightCol) {int midCol = ((rightCol - leftCol) >> 1) + leftCol;int maxRow = getMaxRow(mat, midCol);if ((midCol == 0 || mat[maxRow][midCol] > mat[maxRow][midCol - 1])&& (midCol == mat[0].length - 1 || mat[maxRow][midCol] > mat[maxRow][midCol + 1])) {resCol = midCol;break;}if (midCol == mat[0].length - 1 || mat[maxRow][midCol] > mat[maxRow][midCol + 1]) {rightCol = midCol - 1;} else {leftCol = midCol + 1;}}return new int[]{getMaxRow(mat, resCol), resCol};}private int getMaxRow(int[][] mat, int resCol) {int maxRow = 0;for (int i = 0; i < mat.length; i++) {if (mat[maxRow][resCol] < mat[i][resCol]) {maxRow = i;}}return maxRow;}
相关文章:
)
Leetcode 1901. 寻找峰值 II(Java + 列最大值 + 二分)
题目 1901. 寻找峰值 II 一个 2D 网格中的 峰值 是指那些 严格大于 其相邻格子(上、下、左、右)的元给你一个 从 0 开始编号 的 m x n 矩阵 mat ,其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值 mat[i][j] 并 返回其位置 [i,j] 。你可以假设整个矩阵周边…...

RabbitMQ 消息持久化
默认情况下,exchange、queue、message 等数据都是存储在内存中的,这意味着如果 RabbitMQ 重启、关闭、宕机时所有的信息都将丢失。 RabbitMQ 提供了持久化来解决这个问题,持久化后,如果 RabbitMQ 发送 重启、关闭、宕机ÿ…...

Opencv实验合集——实验四:图片融合
1.概念 图像融合是将两个或多个图像结合在一起,创建一个新的图像的过程。这个过程的目标通常是通过合并图像的信息来获得比单个图像更全面、更有信息量的结果。图像融合可以在许多领域中应用,包括计算机视觉、遥感、医学图像处理等。 融合的方法有很多…...

Java复习
CH1 Java Fundamentals 1.1 Java Features(java特色) 1.1 Simplicity: simple grammar, rich library 简单好用: 语法简单,库文件丰富 1.2 Pure OO: everything is object! 所有程序都是对象 1.3 Security: memory access,…...
腾讯云微服务11月产品月报 | TSE 云原生 API 网关支持 WAF 对象接入
2023年 11月动态 TSE 云原生 API 网关 1、支持使用私有 DNS 解析 服务来源支持私有 DNS 解析器,用户可以添加自己的 DNS 解析器地址进行私有域名解析,适用于服务配置了私有域名的用户。 2、支持 WAF 对象接入 云原生 API 网关对接 Web 安全防火墙&…...

性能优化-待处理
1 性能优化-循环展开...

Linux: sysctl: network: ip_no_pmtu_disc,容易搞混的参数名称
这个参数的迷惑性在于双重否定,字面意思是关闭PMTU发现的功能。如果设置为1,代表关闭;如果是0,代表不关闭pmtu发现的功能。所以说明里,有disable/enable,就容易搞混。所以要甄别网上的某些博客的说明,不要被误导。 ip_no_pmtu_disc - INTEGER Disable Path MTU Discover…...

关于“Python”的核心知识点整理大全26
目录 10.3.9 决定报告哪些错误 10.4 存储数据 10.4.1 使用 json.dump()和 json.load() number_writer.py number_reader.py 10.4.2 保存和读取用户生成的数据 对于用户生成的数据,使用json保存它们大有裨益,因为如果不以某种方式进行存储…...

Axure中继器完成表格的增删改查的自定义元件(三列表格与十列表格)
目录 一、中继器 1.1 定义 1.2 特点 1.3 适用场景 二、三列表格增删改查 2.1 实现思路 2.2 效果演示 三、十列表格增删改查 3.1 实现思路 3.2 效果演示 一、中继器 1.1 定义 在Axure中,"中继器"通常指的是界面设计中的一个元素,用…...

刚clone下来的项目如何上传到新的仓库
查看当前项目的git信息 git remote -v 查看git目录上传到哪个路径下 拉下的项目如何上传到新的仓库 git clone xxxcd xxxrm -r .git 删除原有的git信息,有问题一直回车git init 初始化gitgit add . git commit -m ‘xxx’git remote add origin 远程库地址&#…...
【ARMstm32】【华清远见西安中心】)
面试题总结(十五)【ARMstm32】【华清远见西安中心】
ARM Cortex-M,Cortex-R,Cortex-A的区别和差异是什么? ARM Cortex-M,Cortex-R和Cortex-A是ARM架构下的不同处理器系列,针对不同的应用领域和需求进行了优化和设计。它们之间的区别和差异主要体现在以下几个方面: 1. 应用领域&#…...
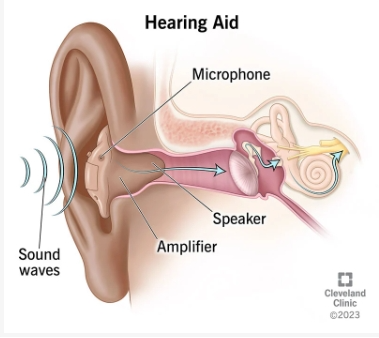
助听器概述
助听器概述 什么是助听器? 助听器是一种放置在耳内或耳后的小型电子设备。助听器可以放大声音,使听力损失的人能够提高他们的听力和言语理解能力。 今天有许多不同类型的助听器,包括处方助听器和非处方 (OTC) 助听器…...
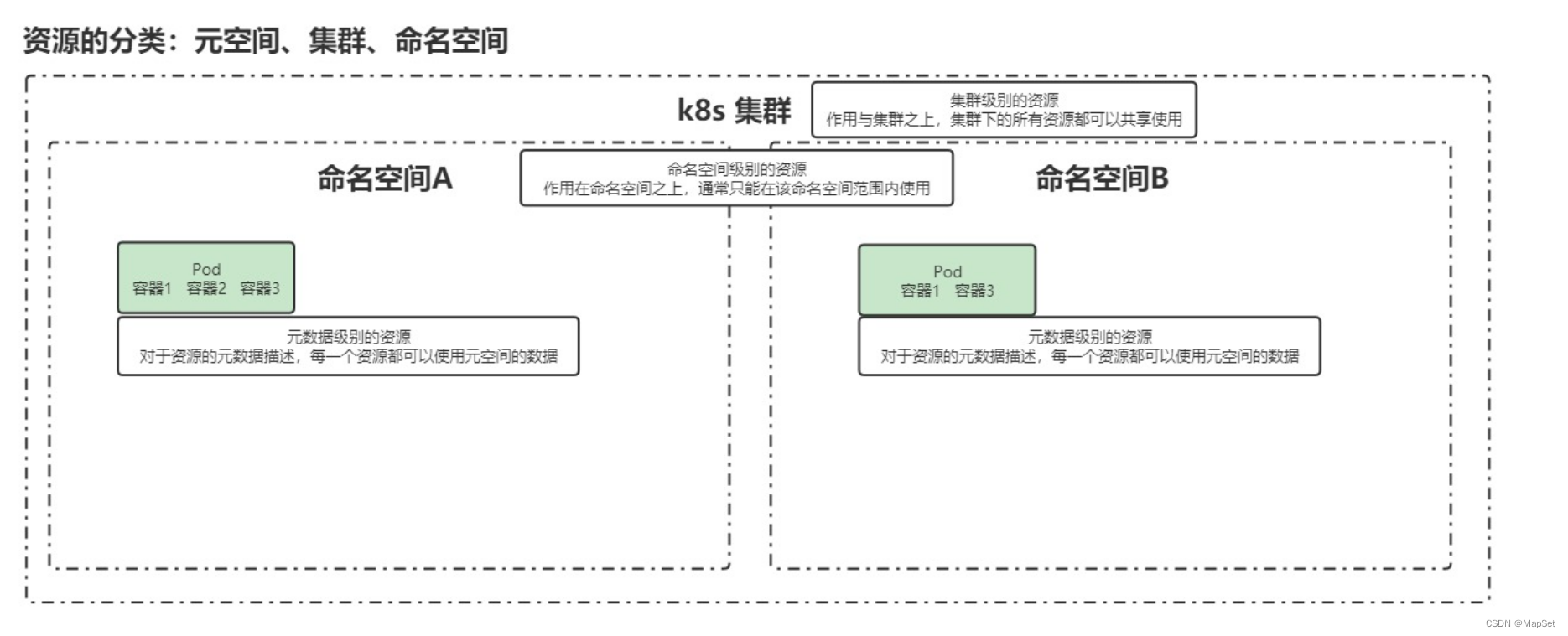
学习k8s
学习k8s 我为什么要用k8s 和其他部署方式的区别是什么? 传统部署方式 java --> package --> 放到服务器上 --> Tomcat 如果是同时进行写操作,会存在并发问题. 用户 --网络带宽–> 服务器 -->服务 同一个服务器上,多个服务: 网络资源的占用 内存的占用 cpu的占…...

iOS 将sdk更新到最新并为未添加版本号的三方库增加版本号
1、更新cocoapod sudo gem install cocoapods2、更新sdk pod update3、查看最新版本号 # 查看最新版本号 cat Podfile.lock4、增加版本号 将查询到的版本号添加到pod中 pod MJRefresh, 3.7.6...
Appium —— 初识移动APP自动化测试框架Appium
说到移动APP自动化测试,代表性的测试框架非Appium莫属,从今天开始我们将从APP结构解析、Appium框架学习、安卓/iOS自动化测试实战、自动遍历回归测试、自动化测试平台及持续集成,多个维度一起由浅入深的学废Appium 今天我们先来初步认识Appi…...

自助式可视化开发,ETLCloud的集成之路
自助式可视化开发 自助式可视化开发是指利用可视化工具和平台,使非技术人员能够自主创建、定制和部署数据分析和应用程序的过程。 传统上,数据分析和应用程序开发需要专业的编程和开发技能。但是,自助式可视化开发工具的出现,使…...
diffu-Distributed inference with multiple GPUs
pytorch的ddp...

在Python中使用Kafka帮助我们处理数据
Kafka是一个分布式的流数据平台,它可以快速地处理大量的实时数据。Python是一种广泛使用的编程语言,它具有易学易用、高效、灵活等特点。在Python中使用Kafka可以帮助我们更好地处理大量的数据。本文将介绍如何在Python中使用Kafka简单案例。 一、安装K…...

进程和线程和协程区别
目录 一、进程和线程 二、线程上下文切换 三、线程与协程区别 一、进程和线程 线程是可以由调度程序对立管理的最小程序指令集,而进程是程序运行的实例。 大多情况下,线程是进程的组成部分,一个进程中可以存在多个线程,这些线…...
银行测试:第三方支付平台业务流,功能/性能/安全测试方法
1、第三方支付平台的功能和结构特点 在信用方面,第三方支付平台作为中介,在网上交易的商家和消费者之间作一个信用的中转,通过改造支付流程来约束双方的行为,从而在一定程度上缓解彼此对双方信用的猜疑,增加对网上购物…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
