23级新生C语言周赛(6)(郑州轻工业大学)
题目链接:ZZULIOJ
3110: 数(shu)数(shu)问题
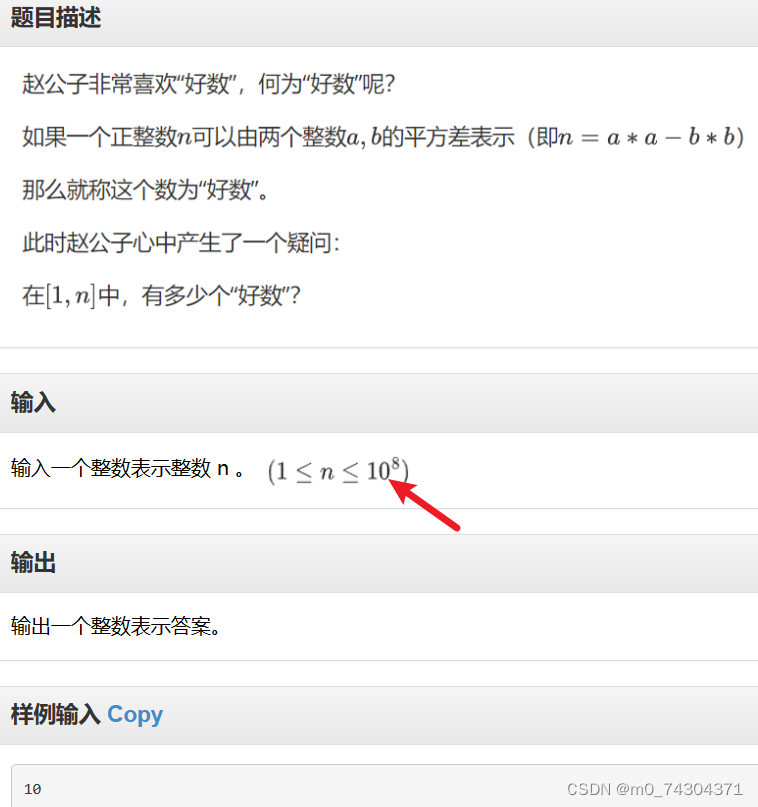
分析:
看到这个题第一步想的是 先把每个平方数给求出来 然后枚举 但是时间复杂度大于1e8 交了一下TLE 但后来打表发现,好数太多了要是枚举的话 注定TLE 能不能间接的去做呢? 把不是的减去,那不就是好数了吗? 这个时候又是打表,会发现要是100以内的好数的话,2 6 10 14 22....不是好数 咱们分析 2 = 2 * 1, 6 = 2 * 3, 10 = 2 * 5, 14 = 2 * 7......so
代码:
#include<bits/stdc++.h>
using namespace std;
int n, m, ret = n;signed main() {cin >> n;ret = n;for(int i = 1, j = 1; 2 * i <= n; i = j * 2 + 1,++j, ret--) {}cout << ret << endl;return 0;
}3111: 点(dian)点(dian)问题

这个题的大致意思就是 在x轴上给你n个点, 让你求一个点x 使得这n个点到这个x的距离是最小的,问你最小的距离是多少?
分析:
这个题是一个典型的 绝对值贪心问题, 这个题的模板是 厂库选址的问题 ,结论是 选的那个点,就是给的这n个点(从小到大排序) 的中位点,也就是中间位置的那个点, 然后枚举这个n个点 ret += abs(a[i] - x) ret就是最后的答案
证明:
设最后选取的点是x 那么这n个点到x的距离就是 dis = |x1 - x| + |x2 - x| + ..... + |xn - x|
第一个和最后一个 第二个和倒数第二个 ..... 结合在一起 这里需要用到的是 |a - x| + |b - x| >= |a - b| 当且仅当 x在a和b的中间的时候 等号成立
因此 这个x只要 都在 每两两结合(第一个和最后一个 第二个和倒数第二个.......)的中间的话 就是最小的 那么 就是中位数那个点 就是最后选择的那个点
代码:
#include<bits/stdc++.h>
#define y1 Y1
#define fi first
#define endl "\n"
#define se second
#define PI acos(-1)
#define int long long
#define pb(x) push_back(x)
#define PII pair<int, int>
#define Yes cout << "Yes\n";
#define No cout << "No\n";
#define YES cout << "YES\n";
#define NO cout << "NO\n";
#define _for(i, a, b) for(int i = a; i <= b; ++i)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;const int N = 2e5 + 10;
int a[N];
int n, m, ret = 0;
string s;signed main() {IOS;cin >> n;_for(i, 1, n)cin >> a[i];int t = a[(n + 2 - 1) / 2]; // a / b向上取整是 (a + b - 1) / b for(int i = 1; i <= n; ++ i ) {ret += abs(a[i] - t);}cout << ret << endl;return 0;
}
/*
贪心问题:
设建在x的位置上 则 距离是
dis = |x1 - x| + |x2 - x| + ..... + |xn - x|
第一个和最后一个 第二个和倒数第二个 ..... 结合在一起 这里需要用到的是 |a - x| + |b - x| >= |a - b| 当且仅当x在a和b的中间的时候 等号成立
因此 这个x只要都在的话 就是最小的 那么 就是中位数那个点 就是答案
*/
相关文章:

23级新生C语言周赛(6)(郑州轻工业大学)
题目链接:ZZULIOJ 3110: 数(shu)数(shu)问题 分析: 看到这个题第一步想的是 先把每个平方数给求出来 然后枚举 但是时间复杂度大于1e8 交了一下TLE 但后来打表发现,好数太多了要是枚举的话 注定TLE 能不能间接的去做呢? 把不是的减去,那不就是好数了吗? 这个时候又是打表,会…...

关于“Python”的核心知识点整理大全24
目录 编辑 10.1.6 包含一百万位的大型文件 pi_string.py 10.1.7 圆周率值中包含你的生日吗 10.2 写入文件 10.2.1 写入空文件 write_message.py programming.txt 10.2.2 写入多行 10.2.3 附加到文件 write_message.py programming.txt 10.3 异常 10.3.1 处理 Ze…...

Vue - 基于Element UI封装一个表格动态列组件
1 组件需求背景 在后台管理系统中,表格的使用频率非常高,统一封装表格动态列组件并全局注册使用,可大大提升代码的复用性和可维护性。 2 全局注册 src/plugins/index.js: import columns from ./columns/indexexport default …...
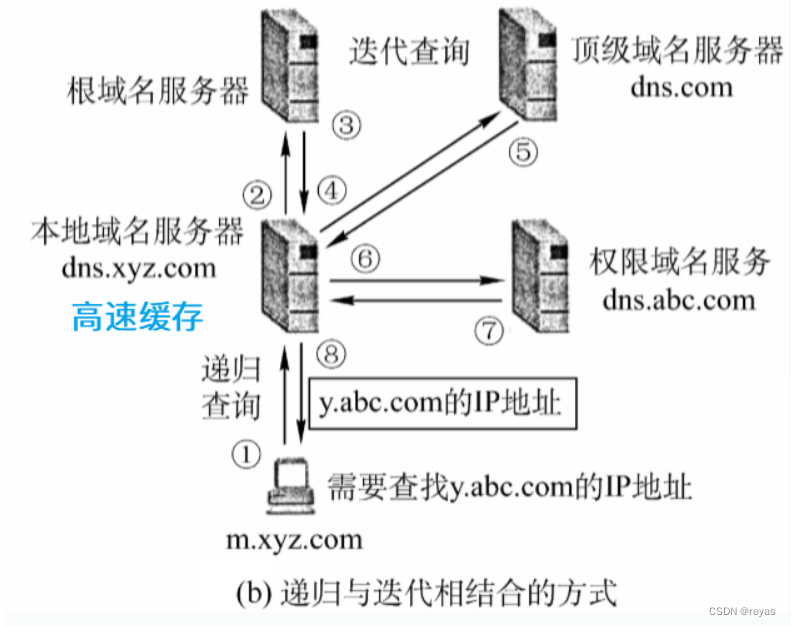
计算机网络:DNS域名解析系统
我最近开了几个专栏,诚信互三! > |||《算法专栏》::刷题教程来自网站《代码随想录》。||| > |||《C专栏》::记录我学习C的经历,看完你一定会有收获。||| > |||《Linux专栏》࿱…...

java面试:==和equals有什么区别?
在 Java 中,"" 和 "equals" 有着不同的作用: "" 运算符: 在基本数据类型(如 int、char 等)中,"" 用于比较它们的值是否相等。 在引用类型中,"&q…...

数字人SaaS系统无限生成AI数字人!
市面上数字人软件层出不穷,选择一款适合的数字人软件是成功的第一步,只需要一款软件就解决数字人直播和数字人短视频的制作,青否数字人SaaS系统(数字人源码:zhibo175)你值得拥有! 青否数字人Saa…...
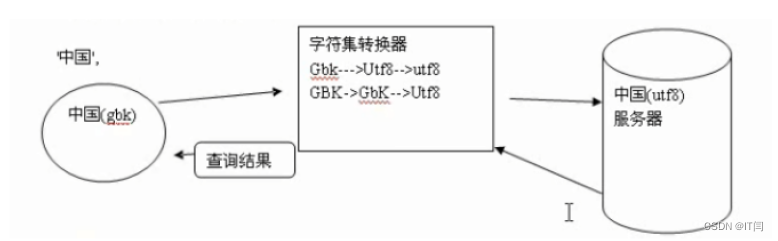
【MySQL】——数据类型及字符集
🎃个人专栏: 🐬 算法设计与分析:算法设计与分析_IT闫的博客-CSDN博客 🐳Java基础:Java基础_IT闫的博客-CSDN博客 🐋c语言:c语言_IT闫的博客-CSDN博客 🐟MySQL:…...

Redis cluster集群设置密码
Redis cluster集群设置密码 1 备份数据 # 链接redis集群,执行rdb快照 bgsave # 备份dump.rdb文件 cp /data/redis/cluster/dump.rdb /data/redis/cluster/backup/dump.rdb.202312202 设置密码 必须保证每个节点的密码保持一致,不然 Redirected 的时候会失败 2.1…...
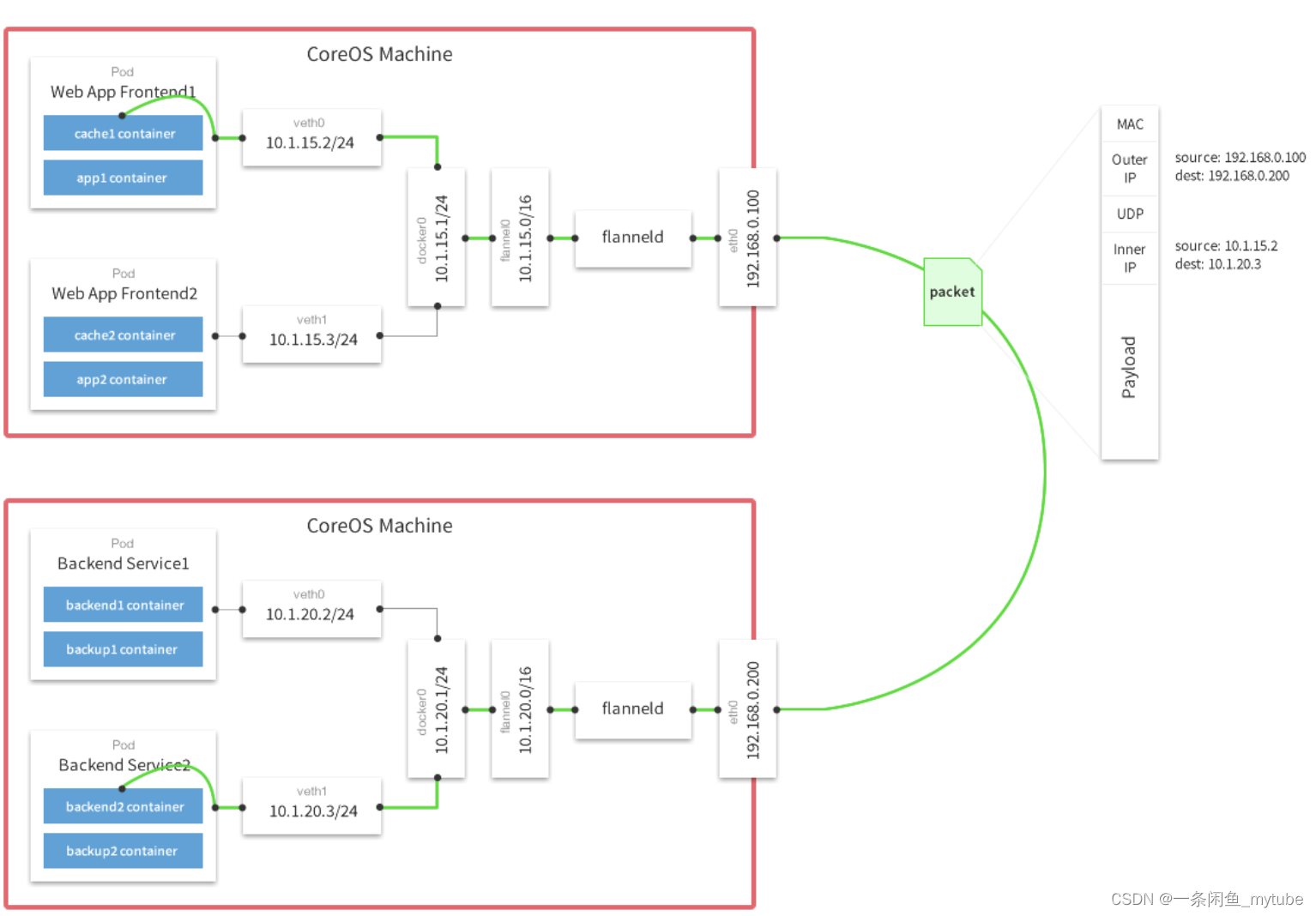
Docker 核心技术
Docker 定义:于 Linux 内核的 Cgroup,Namespace,以及 Union FS 等技术,对进程进行封装隔离,属于操作系统层面的虚拟化技术,由于隔离的进程独立于宿主和其它的隔离的进程,因此也称其为容器Docke…...
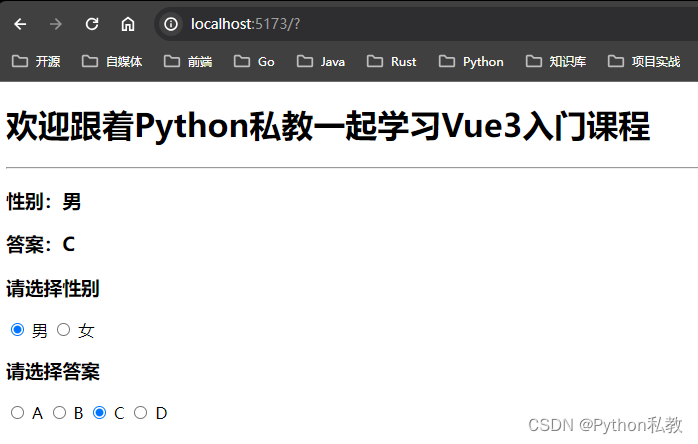
15 使用v-model绑定单选框
概述 使用v-model绑定单选框也比较常见,比如性别,要么是男,要么是女。比如单选题,给出多个选择,但是只能选择其中的一个。 在本节课中,我们演示一下这两种常见的用法。 基本用法 我们创建src/component…...

go语言指针变量定义及说明
go语言指针主要需要记住两个特殊符号, 一个是 & 用来获取变量对应的内存地址 另一个是 * 用来获取指针对应的变量值 下面是个最简单的go语言指针说明 package mainimport "fmt"//指针为内存地址func main() {var a string "指针对应的变量&…...

基于“Galera+MariaDB”搭建多主数据库集群的实例
1、什么是多主数据库集群 多主数据库集群是一种数据库集群架构,每个节点都可以接收写入操作和读取操作,并且通过心跳机制同步数据,保证数据一致性和高可用性。因多主数据库集群每个节点都可以承担读写操作,因此它可以充分利用各个…...
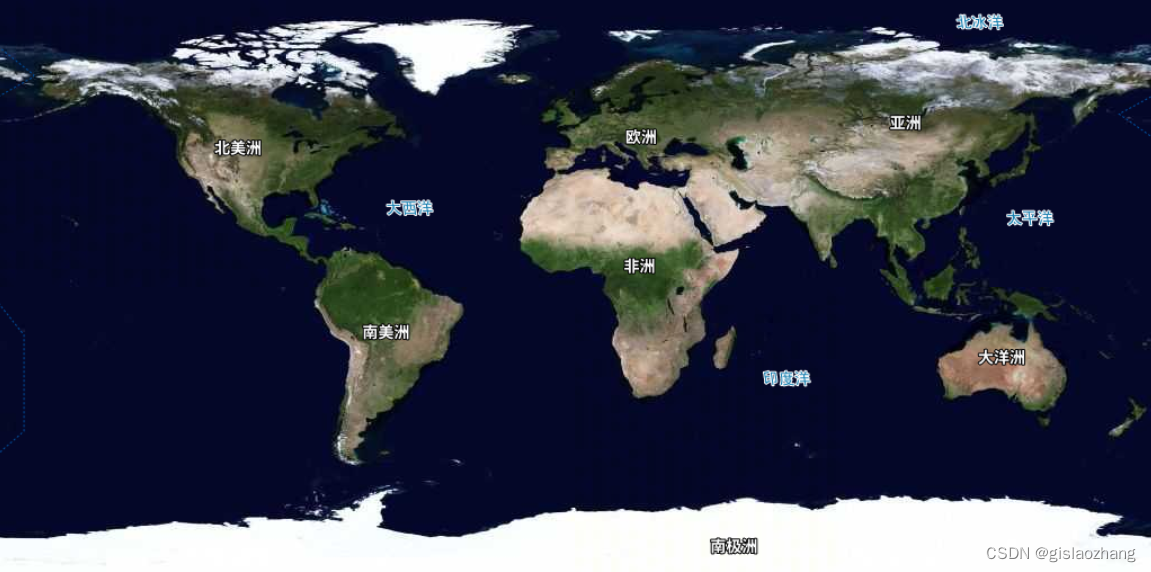
arcgis javascript api4.x加载天地图cgs2000坐标系
需求:arcgis javascript api4.x加载天地图cgs2000坐标系 效果: 示例代码: <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"wid…...

算法学习——回溯算法
回溯算法 理论基础回溯法的效率回溯法解决的问题回溯法模板 组合思路回溯法三部曲 代码 组合(优化)组合总和III思路代码 电话号码的字母组合思路回溯法来解决n个for循环的问题回溯三部曲代码 组合总和思路代码 组合总和II思路代码 理论基础 什么是回溯法…...
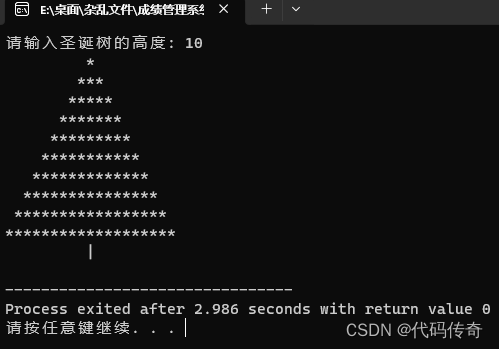
C语言—小小圣诞树
这个代码会询问用户输入圣诞树的高度,然后根据输入的高度在控制台上显示相应高度的圣诞树。 #include <stdio.h>int main() {int height, spaces, stars;printf("请输入圣诞树的高度: ");scanf("%d", &height);spaces height - 1;st…...

Android消息公告上下滚动切换轮播实现
自定义控件 通过继承TextSwitcher实现 直接上代码 public class NoticesSwitcher extends TextSwitcher implements ViewSwitcher.ViewFactory {private Context mContext;private List<Notice> mData;private final long DEFAULT_TIME_SWITCH_INTERVAL 1000;//1spri…...
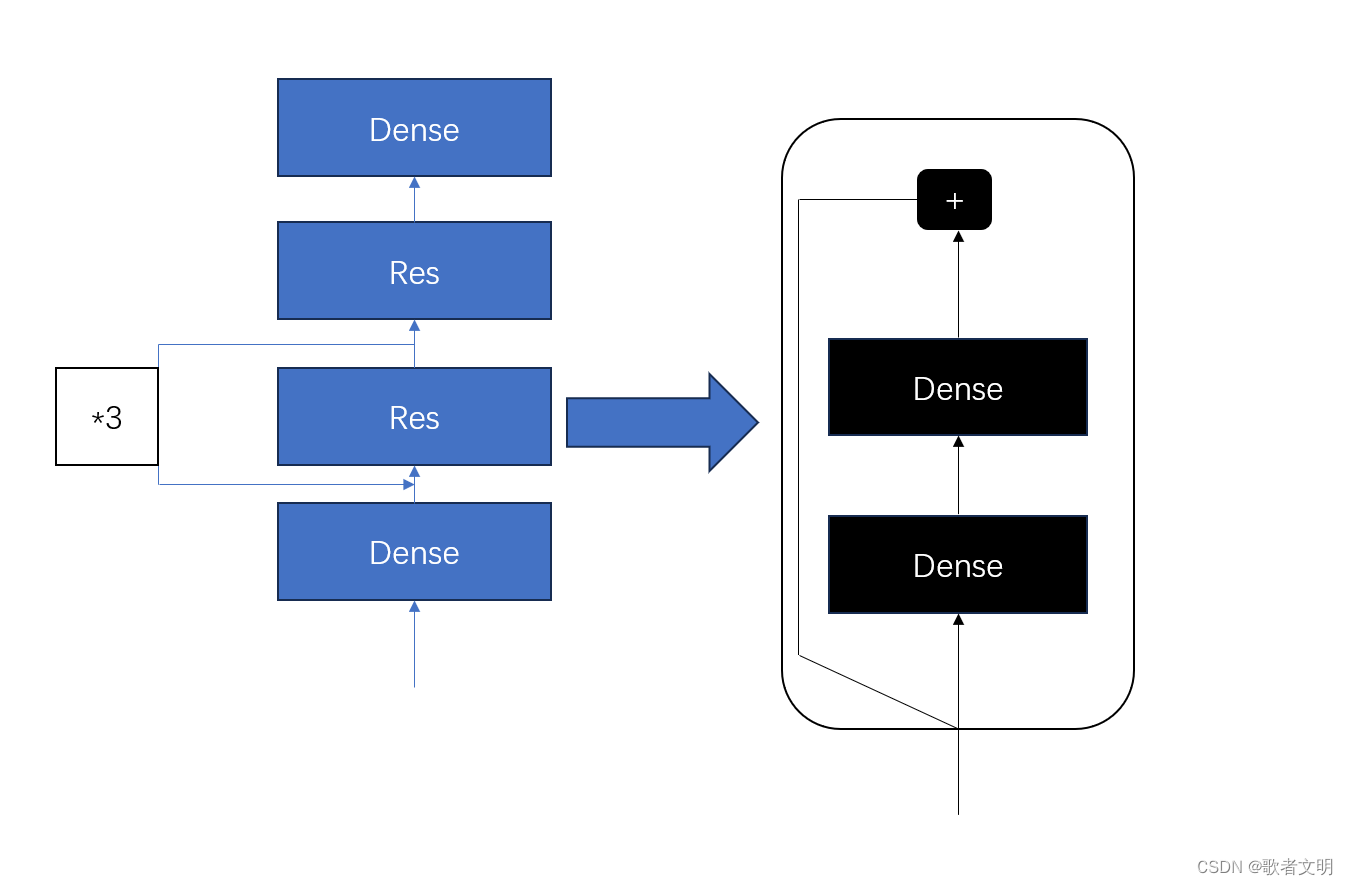
tensorflow入门 自定义模型
前面说了自定义的层,接下来自定义模型,我们以下图为例子 这个模型没啥意义,单纯是为了写代码实现这个模型 首先呢,我们看有几个部分,dense不需要我们实现了,我们就实现Res,为了实现那个*3,我们…...
虚拟机启动 I/O error in “xfs_read_agi+0x95“
1.在选择系统界面按e 进入维护模式 2.找到ro把ro改成 rw init/sysroot/bin/sh 然后按Ctrlx 3.找到坏掉的分区,以nvme0n1p3为例进行修复 xfs_repair -d /dev/nvme0n1p3 4.init 6 重新启动 以下情况 先umount 再修复 则修复成功...

【MYSQL】-库的操作
💖作者:小树苗渴望变成参天大树🎈 🎉作者宣言:认真写好每一篇博客💤 🎊作者gitee:gitee✨ 💞作者专栏:C语言,数据结构初阶,Linux,C 动态规划算法🎄 如 果 你 …...

网络协议小记
一、TCP/IP协议 作为一个小萌新,当然我无法将tcp/ip协议的大部分江山和盘托出,但是其中很多面试可能问到的知识,我觉得有必要总结一下! 首先,在学习tcp/ip协议之前,我们必须搞明白什么是tcp/ip协议。 1、…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
