Stochastic Approximation 随机近似方法的详解之(三)Dvoretzky’s convergence theorem
定理内容
Theorem 6.2 (Dvoretzky’s Theorem). Consider a stochastic process
wk+1=(1−αk)wk+βkηkw_{k+1}=\left(1-\alpha_k\right) w_k+\beta_k \eta_kwk+1=(1−αk)wk+βkηk,
其中{αk}k=1∞,{βk}k=1∞,{ηk}k=1∞\{\alpha_k\}^\infty_{k=1},\{\beta_k\}^\infty_{k=1},\{\eta_k\}^\infty_{k=1}{αk}k=1∞,{βk}k=1∞,{ηk}k=1∞都是随机序列。这里αk≥0,βk≥0{\alpha_k} \ge 0,{\beta_k} \ge 0αk≥0,βk≥0 对于所有的kkk都是成立的。那么 wkw_{k}wk would converge to zero with probability 1 if the following conditions are satisfied:
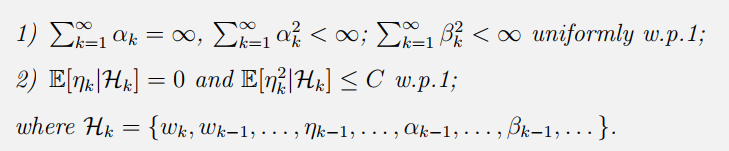
要点阐释
- RM算法里面的αk{\alpha_k}αk是确定性的。然而Dvoretzky’s Theorem中 αk,βk{\alpha_k},{\beta_k}αk,βk 可以是由Hk\mathcal H_kHk决定的随机变量。因此Dvoretzky’s Theorem 更加通用和强大。
- 对于uniformly w.p.1 的解释:

- 不再要求观测误差项ηk\eta_kηk的系数βk\beta_kβk的收敛速度了,收敛的快也没有关系。

证明在这里不展开,需要用到quasimartingales的知识

应用
证明Robbins-Monro theorem:
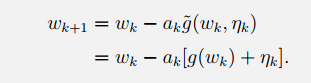
我们在等式两边同时减去目标根:
wk+1−w∗=wk−w∗−ak[g(wk)−g(w∗)+ηk]w_{k+1}-w^*=w_k-w^*-a_k\left[g\left(w_k\right)-g\left(w^*\right)+\eta_k\right]wk+1−w∗=wk−w∗−ak[g(wk)−g(w∗)+ηk]
然后就有:(注意,下面用到了中值定理)
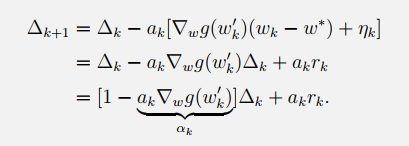
注意这里的αk\alpha_kαk不再是确定的了,而是由wk和wk′w_k和w_k'wk和wk′共同决定的随机序列。对照Dvoretzky’s convergence theorem成立的条件,发现都满足:

到这里也就证明了RM算法求解方程根的收敛性。
定理的扩展:
原定理只能解决单变量的问题,不够使啊。必须扩展一下,让它可以处理多变量。扩展后的Dvoretzky’s convergence theorem 可以用来分析一些随机迭代算法的收敛性:比如Q-learning和TD算法。
扩展后的定理的内容:

在这样的定义下,原先数值上的大小比较就变成了不同向量之间的max norm的比较。注意哈,Hk\mathcal H_kHk是历史数据序列。
顺便解释一下max norm:

定理扩展的一些说明
- 扩展后的定理比原定理更加通用。首先,由于最大范数(the maximum norm)的引入,它可以处理多元变量的情况,对于具有很多个状态的强化学习问题,这一点很重要。第二,相比于原定理对E[ek(x)∣Hk]=0\mathbb{E}\left[e_k(x) \mid \mathcal{H}_k\right]=0E[ek(x)∣Hk]=0 and var[ek(x)∣Hk]≤C\operatorname{var}\left[e_k(x) \mid \mathcal{H}_k\right] \leq Cvar[ek(x)∣Hk]≤C的要求,this theorem only requires that the expectation and variance are bounded by the error ∆k。
- 虽然(6.9)只是针对单个状态,但它可以处理多个状态的原因是是因为条件3和4,它们是针对整个状态空间的。此外, 在应用该定理证明RL算法的收敛性时,我们需要表明(6.9)对每个状态都有效。
参考
https://github.com/MathFoundationRL/Book-Mathmatical-Foundation-of-Reinforcement-Learning
相关文章:

Stochastic Approximation 随机近似方法的详解之(三)Dvoretzky’s convergence theorem
定理内容 Theorem 6.2 (Dvoretzky’s Theorem). Consider a stochastic process wk1(1−αk)wkβkηkw_{k1}\left(1-\alpha_k\right) w_k\beta_k \eta_kwk1(1−αk)wkβkηk, 其中{αk}k1∞,{βk}k1∞,{ηk}k1∞\{\alpha_k\}^\infty_{k1},\{\beta_k\}^\infty_{k1},\…...

7个ES6解构技巧让代码更简洁
您是否厌倦了编写臃肿且难以阅读的代码?想要提升您的编码技能并使您的代码更具可读性和简洁性? 从解构对象和数组到使用默认值和展开运算符,我们将涵盖所有内容,现在,我们将准备好掌握干净简洁的编码艺术。 1.解构对…...

曾经被人们看成是异想天开的产业互联网,或许终将会实现
一波还未平息,一波又起。元宇宙的热度还未彻底散去,ChatGPT已经成为了名符其实的新风口。如果用一个概念来定义现在这样一个热点和风口频出的时代的话,我想,用产业互联网或许是再合适不过的了。对此,可能有人并不认同。…...

log4j控制台不打印日志的故障解决方案
前言 接管了别的项目组的一个代码,在IDAE调试程序的过程中,发现log4j日志居然没有打印在控制台上,日志相关代码也没有问题。 在网上搜索了一圈,总结了一下个人解决这个问题的流程。 流程 1. 判断用了什么配置文件 不知道是出…...
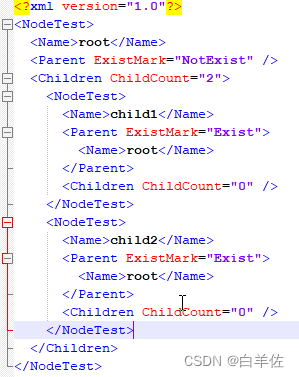
C# 序列化时“检测到循环引用”错误的彻底解决方案
目录 一,问题表现 二、没有技术含量的解决方案 三、本人彻底的解决方案 简要说明 贴代码 思路解析 思路 一,问题表现 示例代码如下: [Serializable] public class NodeTest {public NodeTest (){new List<NodeTest> ();}p…...

小红书“复刻”微信,微信“内造”小红书
配图来自Canva可画 随着互联网增长红利逐渐见顶,各大互联网平台对流量的争夺变得愈发激烈。而为了寻找新的业务可能性,各家都在不遗余力地拓宽自身边界。在此背景下,目前最为“吸睛”和“吸金”的社交、电商、种草、短视频等领域,…...
用arthas轻松排查线上问题
你是否在项目中会碰到以下一些问题: 在代码中打印各种日志来排查,比如方法的入参,出参,及在方法体中打印日志判断走哪行代码还有你觉得代码没问题,可是运行出现却是以前的bug,感觉代码没修改,或…...
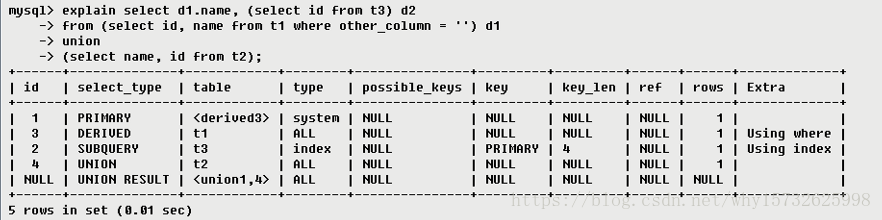
mysql一explain结果分析
1. EXPLAIN简介 使用EXPLAIN关键字可以模拟优化器执行SQL查询语句,从而知道MySQL是如何处理你的SQL语句的。分析你的查询语句或是表结构的性能瓶颈。 ➤ 通过EXPLAIN,我们可以分析出以下结果: 表的读取顺序数据读取操作的操作类型哪些索引可…...

原理底层计划--HashMap
HashMap 之前写了“Java集合TreeMap红黑树一生只爱一次”,说到底还是太年轻了,Map其实在排序中应用比较少,一般追求的是速度,通过HashMap来获取速度。hashmap 调用object hashcode方法用于返回对象的哈希码,主要使用在…...

win10 设备管理器中的黄色感叹号(华硕)
目录一、前言二、原因三、方案四、操作一、前言 打开设备管理器,我们可以看到自己设备的信息,但是在重装系统后,你总会在不经意间发现。咦,怎么多了几个感叹号??? 由于我已经解决该问题&#…...

新产品上市推广不是“铺货”上架
只有不断推出新产品的企业才能走得长远,但现实中往往有很多企业投入了大量人力、物力、财力研发的新产品却在推广的过程中屡屡受挫。那么,为什么适合市场的新产品会在市场营销推广的过程中夭折呢?小马识途营销顾问分析有如下几点:…...

MATLAB训练神经网络小结
MATLAB训练神经网络小结1、一个典型例子1.1 可视化神经网络1.2 指定某一层的激活函数1.3 训练神经网络时使用L1正则化1.4返回训练过程中的参数1.5 查看训练好的权重系数1.6 如何使用早停法来防止过拟合1、一个典型例子 例如输入特征为10维,想训练一个10x20x10x1的三…...
实战:一天开发一款内置游戏直播的国产版Discord应用【附源码】
游戏直播是Discord产品的核心功能之一,本教程教大家如何1天内开发一款内置游戏直播的国产版Discord应用,用户不仅可以通过IM聊天,也可以进行语聊,看游戏直播,甚至自己进行游戏直播,无任何实时音视频底层技术…...
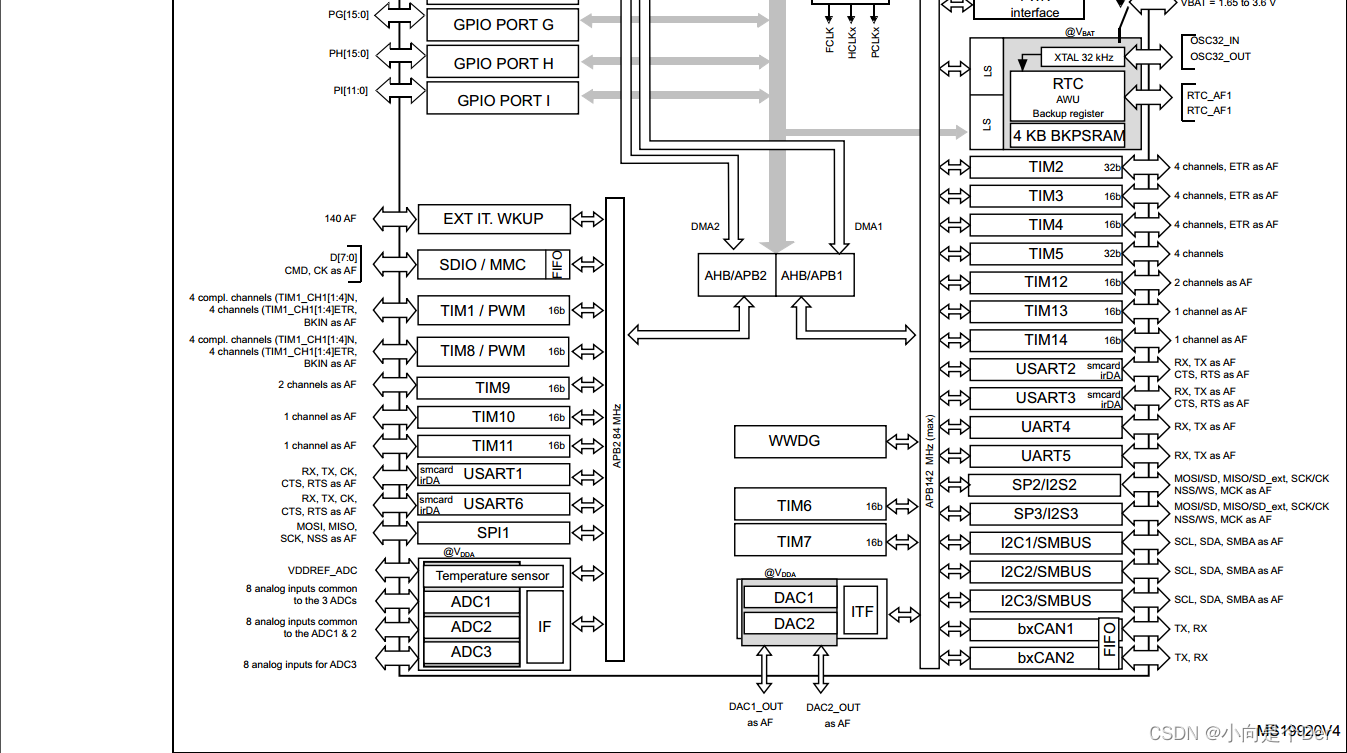
嵌入式学习笔记——基于Cortex-M的单片机介绍
基于Cortex-M的单片机介绍前言生产厂商及其产品线ARM单片机的产品线命名规则留个作业习单片机的资料准备STM32开发所需手册1.芯片的数据手册作业2前言 本文继续接着上一篇中关于Cortex-M的介绍,来记录一些关于ARM系单片机的知识。 生产厂商及其产品线 芯片厂商在…...
Python 虚拟环境的使用
PyCharm 创建的虚拟环境与使用 workon 命令创建的虚拟环境在本质上没有区别,它们都是 Python 的虚拟环境。 使用 PyCharm 创建工程时,使用可以使用曾经工程的虚拟环境,或者新建一个虚拟环境来安装 Python 的库,又或者使用 workon…...

招生咨询|浙江大学MPA项目2023年招生问答与通知
问:报考浙江大学MPA的基本流程是怎么样的? 答:第一阶段为网上报名与确认。MPA考生须参加全国管理类联考,网上报名时间一般为10月初开始、10月下旬截止,错过网上报名时间后不能补报。确认时间一般为11月上旬,…...

Qt std :: bad_alloc
文章目录摘要问题出现原因第一种 请求内存多余系统可提供内存第二种 地址空间过于分散,无法满足大块连续内存的请求第三种 堆管理数据结构损坏稍微总结下没想到还能更新参考关键字: std、 bad、 alloc、 OOM、 异常退出摘要 今天又是被BUG统治的一天&a…...

《设计模式》装饰者模式
《设计模式》装饰者模式 装饰者模式(Decorator Pattern)是一种结构型设计模式,它允许在不改变现有对象结构的情况下,动态地添加行为或责任到对象上。在装饰者模式中,有一个抽象组件(Component)…...
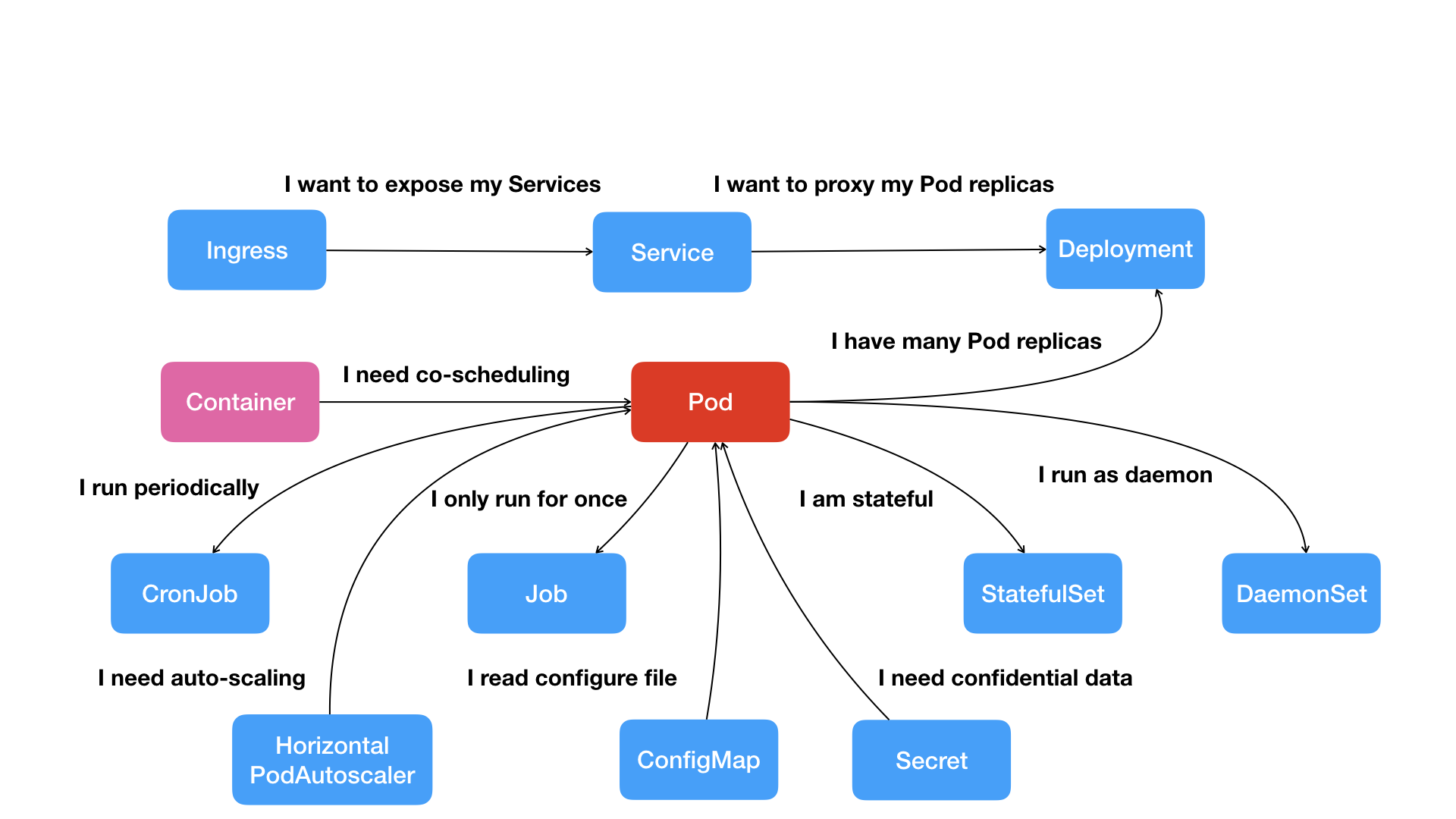
一文说清Kubernetes的本质
文章目录Kubernetes解决了什么问题?Kubernetes的全局架构Kubernetes的设计思想Kubernetes的核心功能Kubernetes如何启动一个容器化任务?Kubernetes解决了什么问题? 编排?调度?容器云?还是集群管理…...
信息发布小程序【源码好优多】
简介 信息发布小程序,实现数据与小程序数据同步共享,通过简单的配置就能搭建自己的小程序。,基于微信小程序开发的小程序。 这个框架比较简单就是用微信原生开发技术进行实现的,可以用于信息展示等相关信息。其中目前APP比较多&am…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...
