Java解决比特维位计数
Java解决比特维位计数
01 题目
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
示例 1:
输入:n = 2
输出:[0,1,1]
解释:
0 --> 0
1 --> 1
2 --> 10
示例 2:
输入:n = 5
输出:[0,1,1,2,1,2]
解释:
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
提示:
0 <= n <= 105
02 知识点
-
动态规划(DP)
-
二进制原理
03 我的题解
public class dongtai01 {public static void main(String[] args) {//测试和检查数据int[] nums=countBits(2);for (int i = 0; i < nums.length; i++) {System.out.println(nums[i]);}}public static int[] countBits(int n) {//根据题设得到返回数组int[] nums=new int[n+1];//循环判断每一个数的二进制有几个1for (int i = 0; i < nums.length; i++) {nums[i]=countBit(i);}return nums;}public static int countBit(int n) {//计数器int count=0;//当n=0时终止while (n!=0) {//根据二进制转化原理,二进制是十进制不断除以2的余数if (n%2==1) {//当余数为1时,计数器加一count++;}//下一次循环前除2n=n/2;}return count;}
}
相关文章:

Java解决比特维位计数
Java解决比特维位计数 01 题目 给你一个整数 n ,对于 0 < i < n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n 1 的数组 ans 作为答案。 示例 1: 输入:n 2 输出:[0,1,1] 解释&a…...

【深度学习目标检测】九、基于yolov5的路标识别(python,目标检测)
YOLOv5是目标检测领域一种非常优秀的模型,其具有以下几个优势: 1. 高精度:YOLOv5相比于其前身YOLOv4,在目标检测精度上有了显著的提升。YOLOv5使用了一系列的改进,如更深的网络结构、更多的特征层和更高分辨率的输入图…...
PyCharm添加自动函数文档注释
目录 1、背景2、开启PyCharm自动函数文档注释 1、背景 规范的函数文档注释有助于他人理解代码,便于团队协作、提高效率。但如果我们自己手写函数文档注释将非常耗时耗力。PyCharm安装后默认没有开启自动化函数文档注释,需要我们开启 2、开启PyCharm自动…...
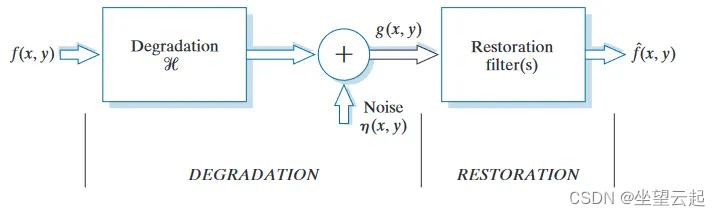
数字图像处理 基于Numpy、PyTorch在频率空间中建模运动模糊
一、简述 运动模糊在图像中很常见,它会降低图像的价值,因为它会破坏图像中包含的数据。在计算机视觉中,通常通过使用许多不同的模糊增强来训练神经网络以适应这种模糊。建模模糊或图像退化的概念来自图像恢复,这是逆转退化影响的过程,以便人类或算法可以辨别原始捕获的数据…...
海康威视对讲广播系统 RCE漏洞复现(CVE-2023-6895)
0x01 产品简介 Hikvision Intercom Broadcasting System是中国海康威视(Hikvision)公司的一个对讲广播系统。 0x02 漏洞概述 Hikvision Intercom Broadcasting System 3.0.3_20201113_RELEASE(HIK)版本存在操作系统命令注入漏洞,该漏洞源于文件/php/ping.php的参数jsonda…...

【优化】Springboot 修改 tomcat连接池
【优化】Springboot 修改 tomcat连接池 factory.setTomcatProtocolHandlerCustomizers(tomcatProtocolHandlerCustomizers); 可以更换为 虚拟线程连接池 package org.config.init;import org.apache.catalina.Context; import org.apache.catalina.core.AprLifecycleListener…...

百度侯震宇:AI原生与大模型将从三个层面重构云计算
12月20日,2023百度云智大会智算大会在北京举办,大会以「大模型重构云计算,Cloud for AI」为主题,深度聚焦大模型引发的云计算变革。 百度智能云表示,为满足大模型落地需求,正在基于「云智一体」战略重构…...
【SpringBoot快速入门】(2)SpringBoot的配置文件与配置方式详细讲解
之前我们已经学习的Spring、SpringMVC、Mabatis、Maven,详细讲解了Spring、SpringMVC、Mabatis整合SSM的方案和案例,上一节我们学习了SpringBoot的开发步骤、工程构建方法以及工程的快速启动,从这一节开始,我们开始学习SpringBoot…...
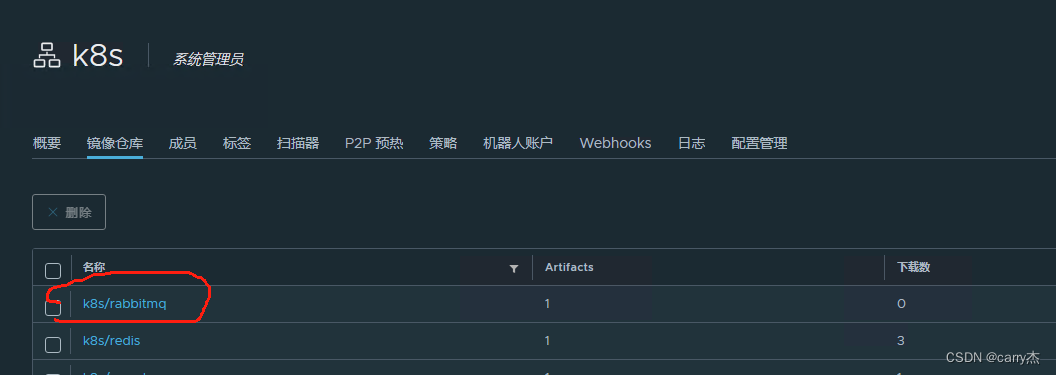
麒麟V10 ARM 离线生成RabbitMQ docker镜像并上传Harbor私有仓库
第一步在外网主机执行: docker pull arm64v8/rabbitmq:3.8.9-management 将下载的镜像打包给离线主机集群使用 在指定目录下执行打包命令: 执行: docker save -o rabbitmq_arm3.8.9.tar arm64v8/rabbitmq:3.8.9-management 如果懒得打包…...
AI创作系统ChatGPT商业运营网站系统源码,支持AI绘画,GPT语音对话+DALL-E3文生图
一、前言 SparkAi创作系统是基于ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI创作Ch…...

剑指offer题解合集——Week1day5
剑指offerWeek1 周五:重建二叉树 题目链接:重建二叉树 输入一棵二叉树前序遍历和中序遍历的结果,请重建该二叉树。注意:二叉树中每个节点的值都互不相同; 输入的前序遍历和中序遍历一定合法; 数据范围 树中节点数量…...
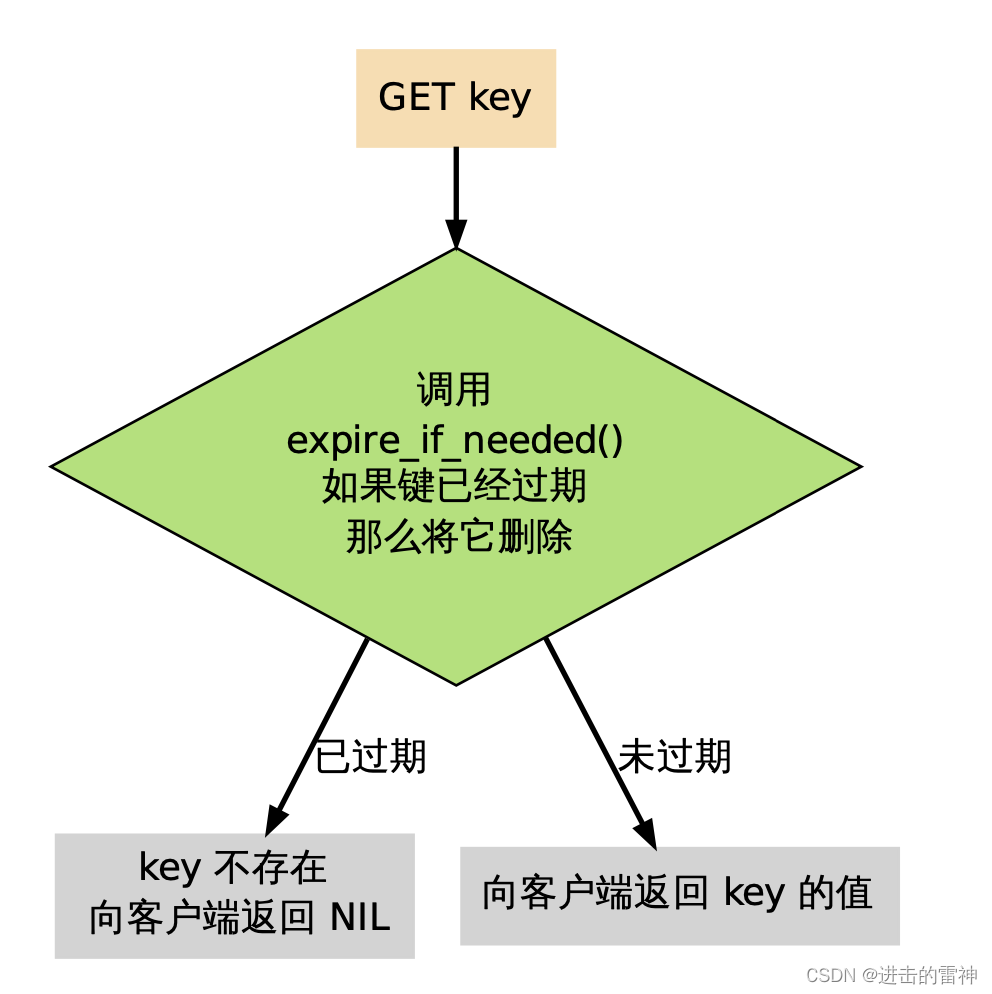
Redis设计与实现之数据库
目录 一、数据库 1、数据库的结构 2、 数据库的切换 3、 数据库键空间 4、键空间的操作 添加新键 删除键 更新键 取值 其他操作 5、 键的过期时间 6、过期时间的保存 7、设置生存时间 8、过期键的判定 9、 过期键的清除 定时删除 惰性删除 定期删除 10、过期…...
如何在Eclipse中安装WindowBuilder插件,详解过程
第一步:找到自己安装eclipse的版本,在Help-关于eclipse里面,即Version 第二步:去下面这个网站找到对应的 link(Update Site),这一步很重要,不然版本下载错了之后还得删除WindowBuil…...
node.js mongoose schemaTypes
目录 官方文档 简介 SchemaType 示例 配置SchemaType规则 通用规则 特定schemaType规则 String Number Date Map monggose会根据shcemaType将文档值转换成指定的类型 官方文档 Mongoose v8.0.3: SchemaTypes 简介 SchemaTypes是在使用Mongoose时,用于…...
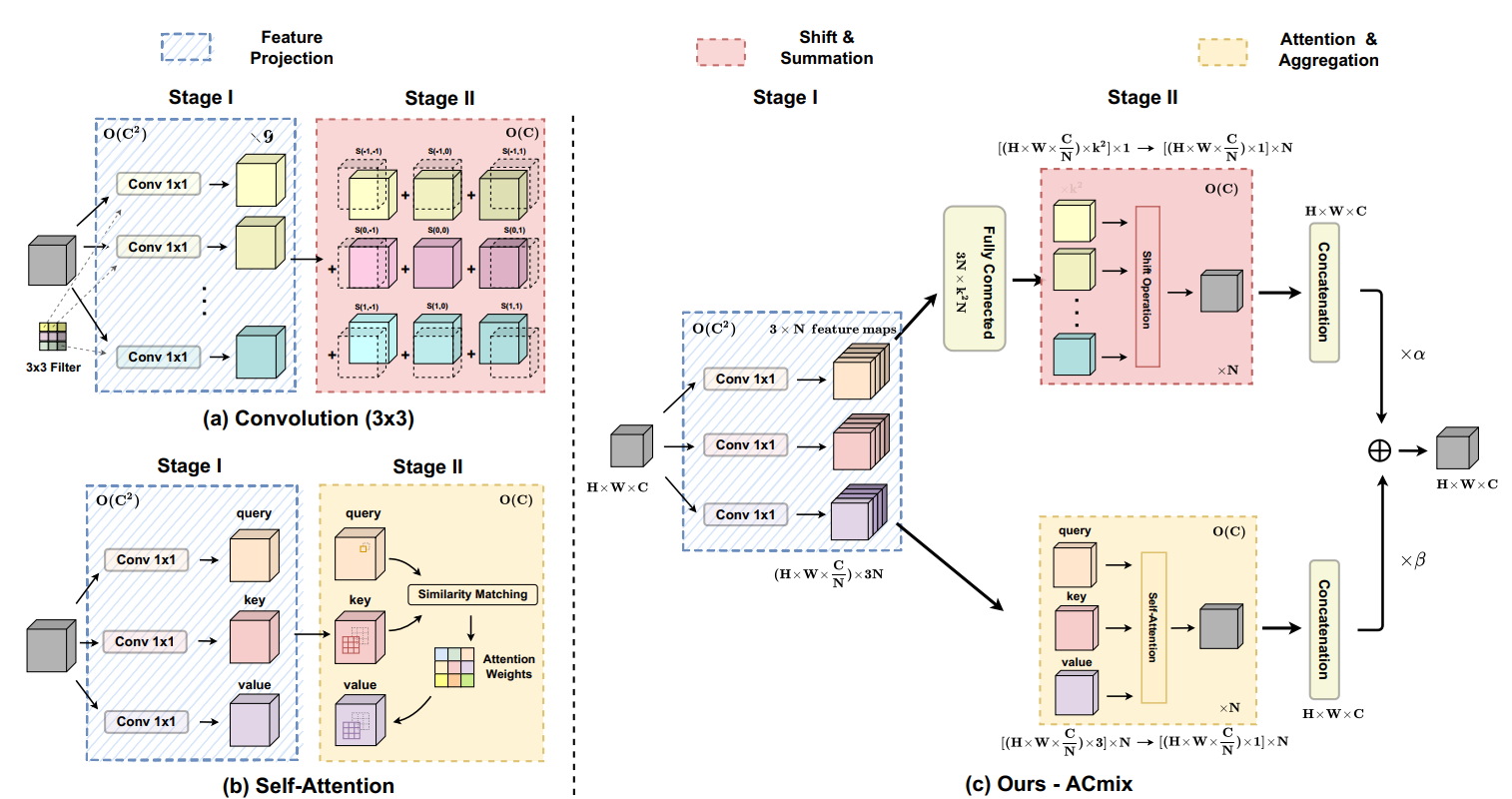
论文解读:On the Integration of Self-Attention and Convolution
自注意力机制与卷积结合:On the Integration of Self-Attention and Convolution(CVPR2022) 引言 1:卷积可以接受比较大的图片的,但自注意力机制如果图片特别大的话,运算规模会特别大,即上图中右边(卷积)会算得比较快…...

【Spring】15 ApplicationContextAware 接口
文章目录 1. 简介2. 作用3. 使用3.1 创建并实现接口3.2 配置 Bean 信息3.3 创建启动类3.4 启动 4. 应用场景总结 Spring 框架提供了许多回调接口,用于在 Bean 的生命周期中执行特定的操作。ApplicationContextAware 接口是其中之一,它允许 Bean 获取对 A…...

Android 版本控制工具--Git
要在Android中使用Git,需要进行以下步骤: 安装Git:首先在你的开发环境中安装Git。在Windows中,你可以从官方网站(https://git-scm.com/downloads)上下载Git的可执行文件并进行安装。在Mac上,你可…...

Wireshark高级网络安全分析
第一章:Wireshark基础及捕获技巧 1.1 Wireshark基础知识回顾 1.2 高级捕获技巧:过滤器和捕获选项 1.3 Wireshark与其他抓包工具的比较 第二章:网络协议分析 2.1 网络协议分析:TCP、UDP、ICMP等 2.2 高级协议分析:HTTP…...
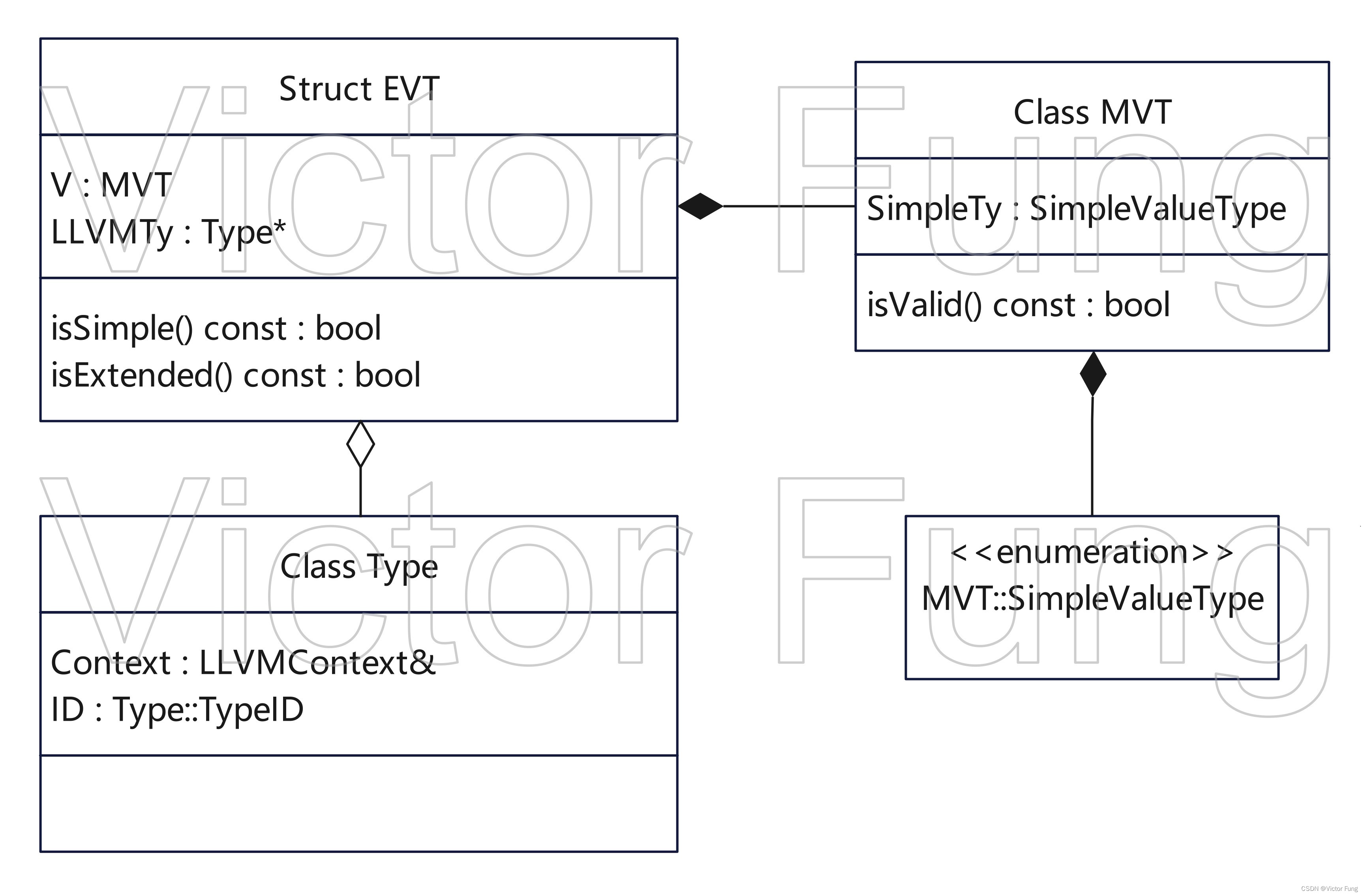
llvm后端之DAG设计
llvm后端之DAG设计 引言1 核心类设计2 类型系统2.1 MVT::SimpleValueType2.2 MVT2.3 EVT 3 节点类型 引言 llvm后端将中端的IR转为有向无环图,即DAG。如下图: 图中黑色箭头为数据依赖;蓝色线和红色线为控制依赖。蓝色表示指令序列化时两个节…...
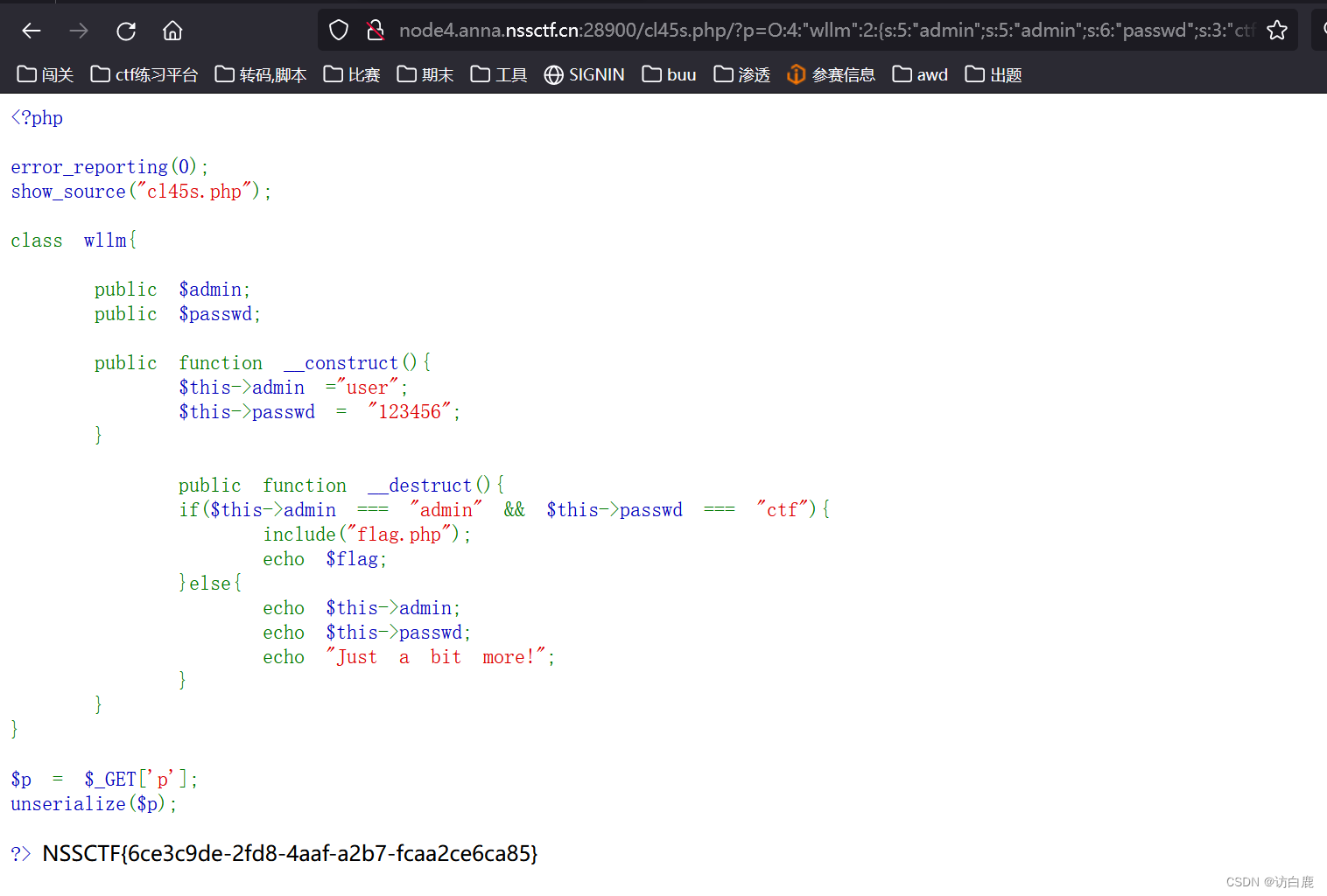
反序列化 [SWPUCTF 2021 新生赛]ez_unserialize
打开题目 查看源代码 得到提示,那我们用御剑扫描一下看看 我们知道有个robots.txt,访问一下得到 那我们便访问一下 cl45s.php看看 得到网站源代码 <?phperror_reporting(0); show_source("cl45s.php");class wllm{public $admin;public …...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
