递归算法:二叉树前序、中序、后序遍历解析与递归思想深度剖析

文章目录
- 一、二叉树的遍历
- 1.1 链式结构二叉树的创建
- 1.1 二叉树结构图
- 二、 前序遍历
- 代码演示:
- 2.1 前序遍历递归展开图
- 三、中序遍历
- 代码演示:
- 四、后序遍历
- 代码演示:
- 五、二叉树的层序遍历
- 5.1 层序遍历的思想
- 📝文章结语:
一、二叉树的遍历
学习二叉树链式结构,最简单的方式就是遍历。所谓 二叉树遍历(Traversal) 是按照某种特定的规则,依次对二叉树中的结点进行相应的操作,并且每个结点只操作一次。
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 前序遍历
( Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。 - 中序遍历
( Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。 - 后序遍历
( Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后
访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
1.1 链式结构二叉树的创建
这里只是模拟创建一下链式二叉树真正的结构并不是这样创建的:
📚 代码演示:
#include<stdio.h>
#include<stdlib.h>typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;//创建节点
BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc file");exit(-1);}node->data = x;node->left = NULL;node->right = NULL;return node;
}int main()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;PreOrder(node1);return 0;
}1.1 二叉树结构图

二、 前序遍历
前序遍历( Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
- 也就是先访问堆顶然后再访问左子树 (但是要保证每个子树都是这样遍历的)
- 而这个情况用递归在合适不过了,简直就是非常的简单。大家看下这段代码看看理解嘛?
代码演示:
//前序遍历
void PreOrder(BTNode* root)
{if (root == NULL)return;printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);
}
是不是非常震惊,只需要几行代买就解决前序遍历的问题,这就是递归思想
- 大问题化简成递归小问题
🍹递归的技巧
大问题转化为子问题
以及递归的结束条件
2.1 前序遍历递归展开图
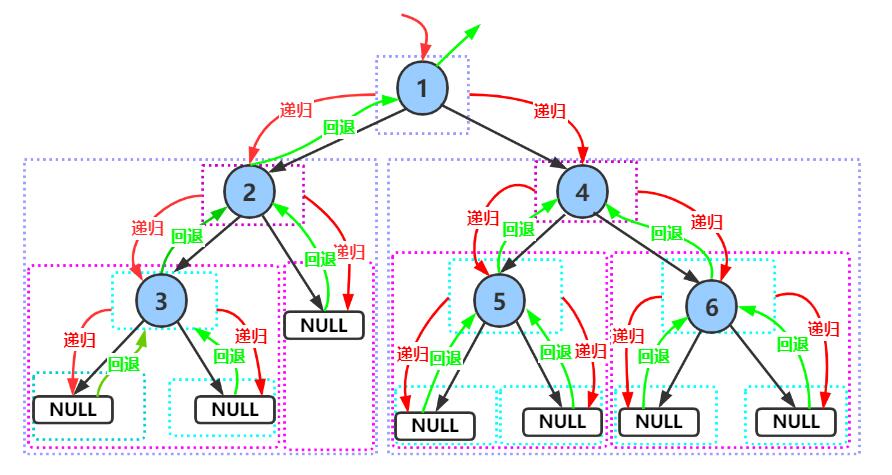
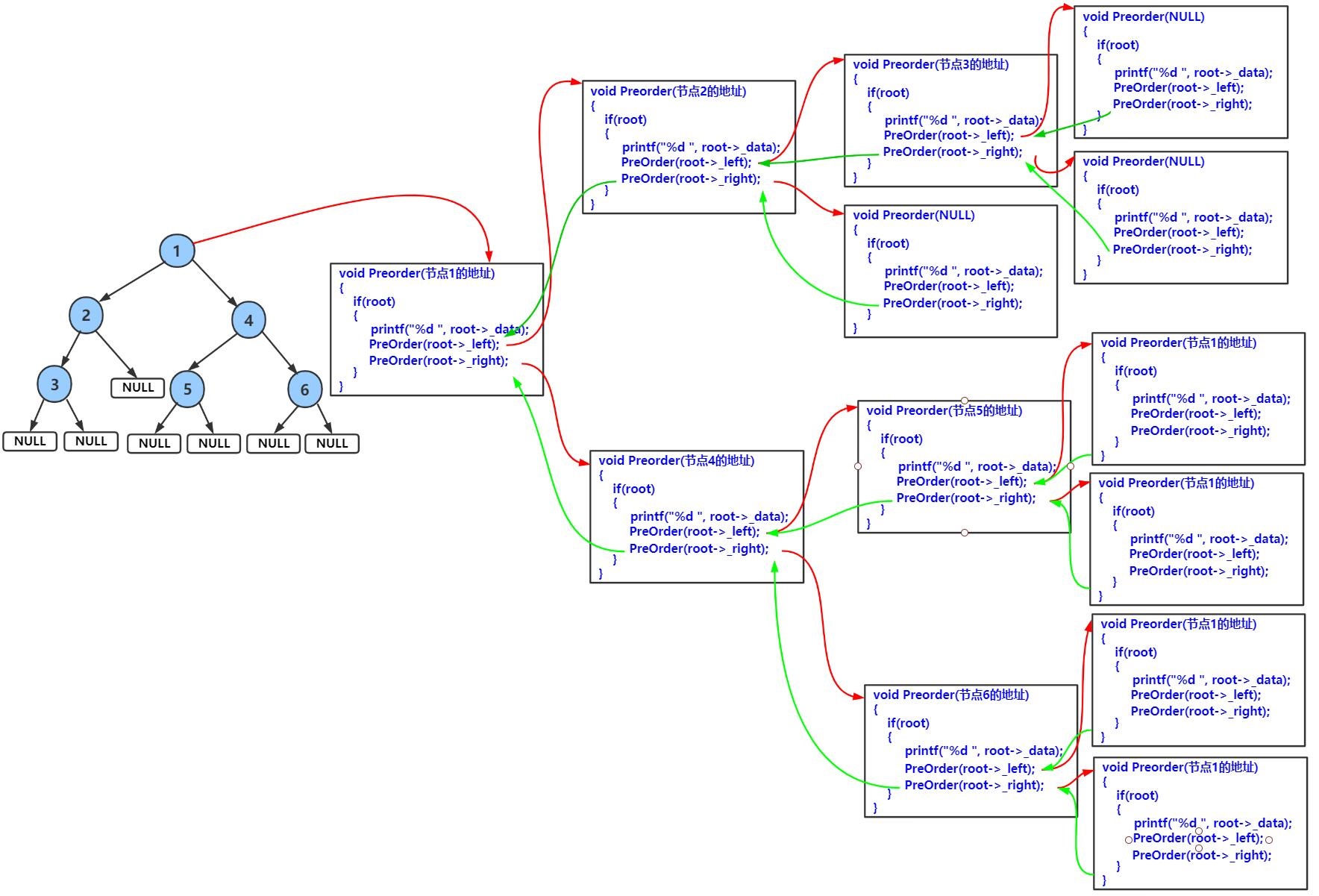
三、中序遍历
有了前序遍历的经验我们接下来中序遍历简直就是 直接秒杀
- 直接照猫画虎就好了
代码演示:
//中序遍历
void InOrder(BTNode* root)
{if (root == NULL)return;InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}
四、后序遍历
代码演示:
//后序遍历
void PostOrder(BTNode* root)
{if (root == NULL)return;PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}
五、二叉树的层序遍历
层序遍历就是从所在二叉树的根结点出发,首先访问第一层的树根结点,然后从左到右访问第2层上的结点,接着是第三层的结点.
- 以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。

5.1 层序遍历的思想
层序遍历大家看到一层一层遍历不知道对,我们前面学的数据结构 队列 是否有想法也是和层序一样:
- 从跟进去然后是左右子树,子树又是左右子树
- 每次把根 打印出来就把他的子树带进去 然后删除跟
- 这样是不是就是前一层带后一层的子树了
📚 代码演示:
// 层序遍历
void LevelOrder(BTNode* root)
{Que q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);printf("%d ", front->data);if(front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);QueuePop(&q);}
}
📝文章结语:
☁️ 把本章的内容全部掌握,铁汁们就可以熟练应用switch语句啦!
看到这里了还不给博主扣个:
⛳️ 点赞🍹收藏 ⭐️ 关注!
💛 💙 💜 ❤️ 💚💓 💗 💕 💞 💘 💖
拜托拜托这个真的很重要!
你们的点赞就是博主更新最大的动力!
有问题可以评论或者私信呢秒回哦。

相关文章:

递归算法:二叉树前序、中序、后序遍历解析与递归思想深度剖析
🎬 鸽芷咕:个人主页 🔥 个人专栏: 《linux深造日志》 《高效算法》 ⛺️生活的理想,就是为了理想的生活! 文章目录 一、二叉树的遍历1.1 链式结构二叉树的创建1.1 二叉树结构图 二、 前序遍历代码演示:2.1 前序遍历递…...
WebGL开发数字孪生项目
WebGL(Web Graphics Library)是一种用于在Web浏览器中渲染交互式3D图形的JavaScript API。虽然WebGL本身并不是一个数字孪生开发框架,但它提供了强大的图形渲染功能,可以用于开发与数字孪生相关的项目。以下是一些可以使用WebGL开…...
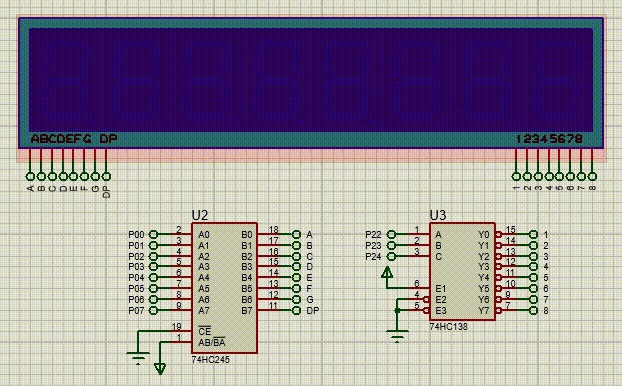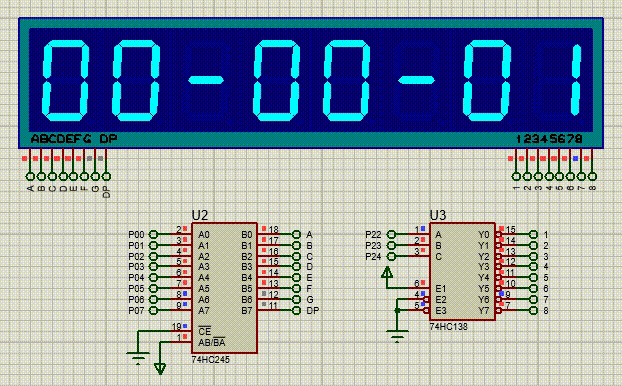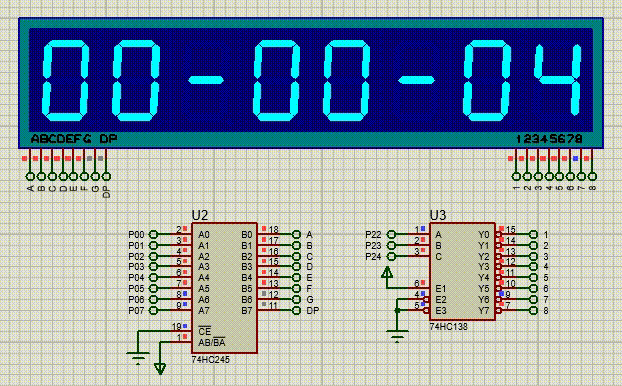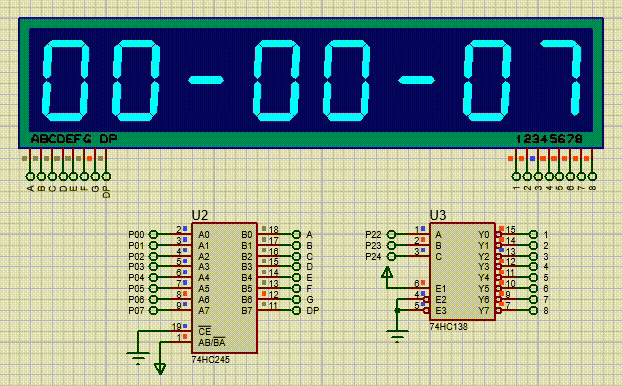
【51单片机系列】C51中的中断系统扩展实验
本文是关于51单片机中断系统的扩展实验。 文章目录 一、 扩展实验一:使用外部中断0控制蜂鸣器,外部中断1控制直流电机二、扩展实验二:修改定时器初值,设定3秒钟的定时时间让LED模块闪烁三、扩展实验三:使用定时器1和数…...
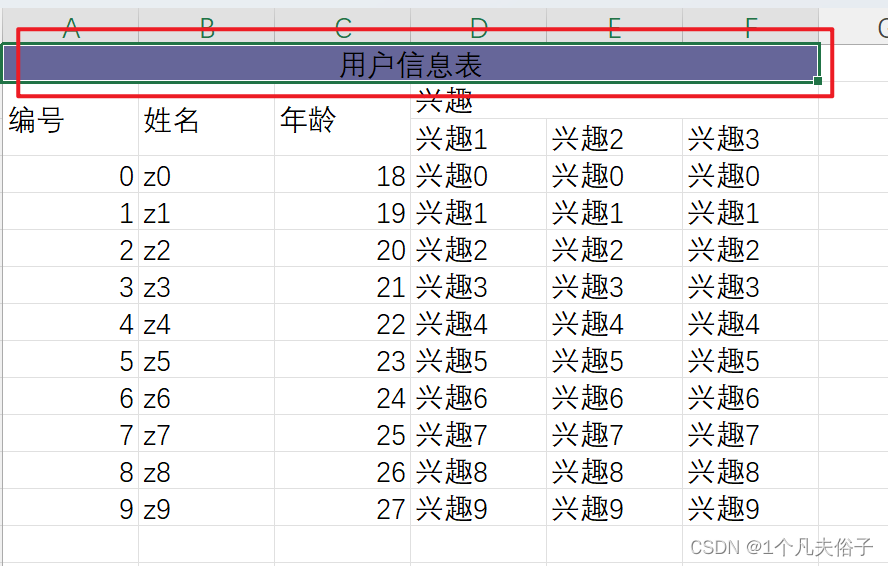
Poi实现复杂Excel导出,理解POI操作Excel思路!!!
前言 对于简单excel报表导出,有很多简单的工具如easypoi,而且现在网上已经有很多工具类整合easypoi使用起来非常方便。但是简单的弊端往往无法适配一些负责场景,而我们实际生产中面临的都是客户自定以的一个负责报表导出,这是利用…...

关于 jsconfig.json 文件在导入文件路径提示方面
前文:以前我弄不清 jsconfig.json 文件的作用是什么,只觉得 tsconfig.json 文件是用来 ts 编译的配置项,js 又不用编译为什么会需要 jsconfig.json 文件。搬了这么久的砖,也算是有所心得,今日记下以备不时之需。 jsco…...
验证码:防范官网恶意爬虫攻击,保障用户隐私安全
网站需要采取措施防止非法注册和登录,验证码是有效的防护措施之一。攻击者通常会使用自动化工具批量注册网站账号,以进行垃圾邮件发送、刷量等恶意活动。验证码可以有效阻止这些自动化工具,有效防止恶意程序或人员批量注册和登录网站。恶意程…...
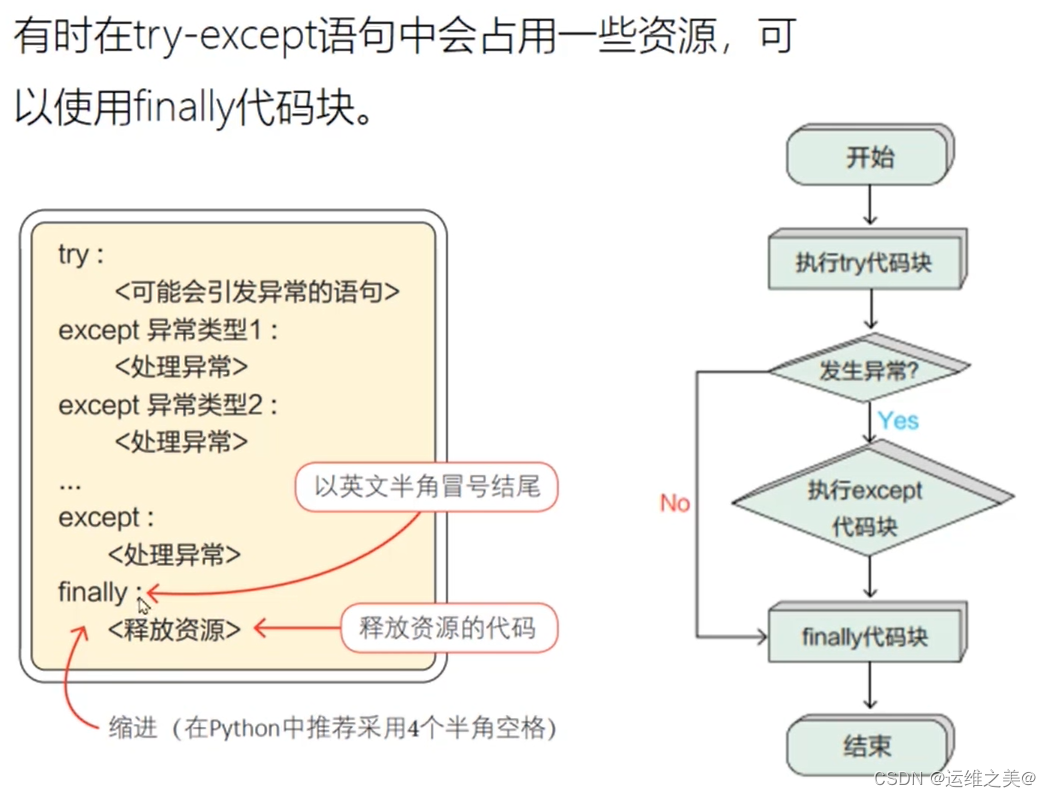
python学习笔记--异常捕获
异常场景 numinput("input you number:") n9000 try:resultn/int(num)print({} 除以num 结果为{}.format(n,result)) except ZeroDivisionError as err:print("0不可以作为除数,出现报错{}".format(err)) except ValueError as err:print(&quo…...
ChatGPT如何计算token数?
GPT 不是适用于某一门语言的大型语言模型,它适用于几乎所有流行的自然语言。所以 GPT 的 token 需要 兼容 几乎人类的所有自然语言,那意味着 GPT 有一个非常全的 token 词汇表,它能表达出所有人类的自然语言。如何实现这个目的呢?…...

页面菜单,通过get请求一个url后,跳转另外一个页面,+丢失问题
业务场景描述: 在A系统,菜单点击跳B系统这个操作。 A系统菜单是get请求到B系统的一个缓冲页面,然后这个缓冲页面获取到url中的accessToken后,在这个页面中通过post请求后端接口。 问题描述: 当accessToken中包含了…...

高并发场景下的延时双删
基本介绍 "延时双删"是一种在并发编程中使用的技术,用于处理缓存和数据库之间的数据一致性问题。在高并发的场景下,这种方法特别有用。下面是对延时双删的详细介绍: 基本概念: 缓存与数据库的不一致:在并发…...

log4js-node在nodejs项目中的使用示例
在Node.js项目中使用log4js-node模块可以帮助你记录日志。以下是一个简单的示例,演示了如何在Node.js项目中使用log4js-node模块: 首先,你需要安装log4js-node模块。在终端中执行以下命令: npm install log4js 接下来ÿ…...
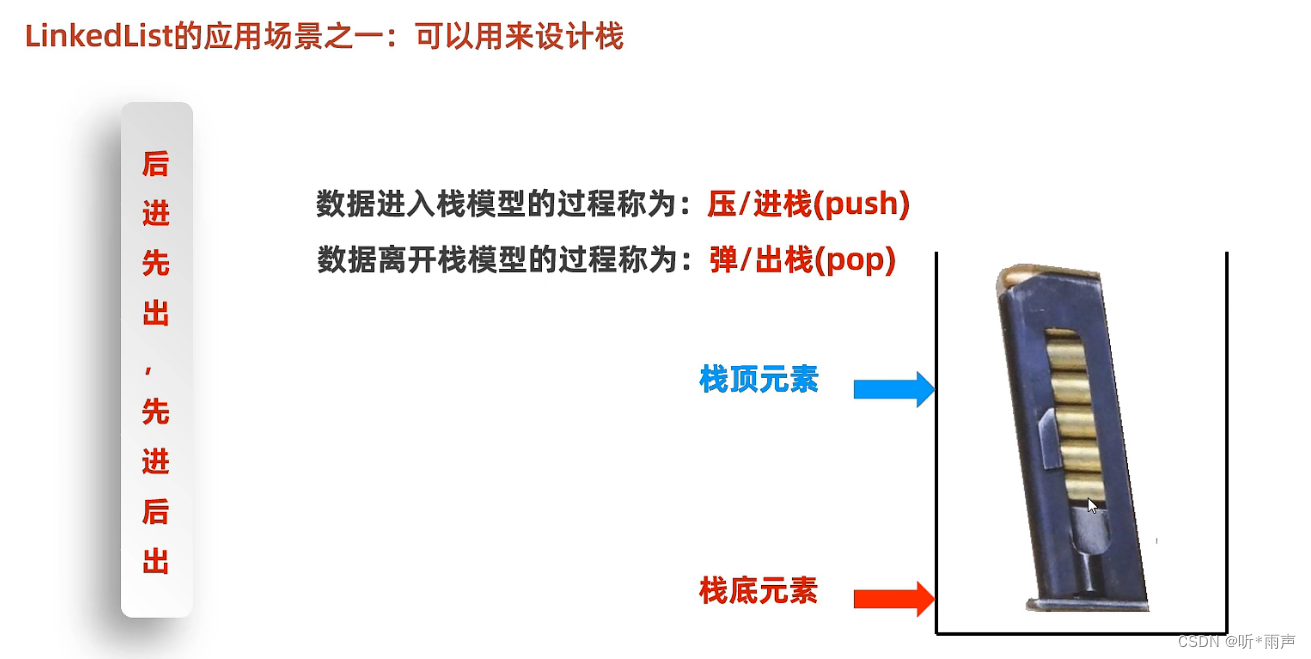
Java_集合进阶(Collection和List系列)
一、集合概述和分类 1.1 集合的分类 已经学习过了ArrayList集合,但是除了ArrayList集合,Java还提供了很多种其他的集合,如下图所示: 我想你的第一感觉是这些集合好多呀!但是,我们学习时会对这些集合进行…...
)
QT GUI代码大全(MainWindow, QFile, QPainter, QGraphicsItem/Scene/View)
文章目录 窗口设置QMainWindow类 按钮和菜单QMenuBar类QMenu类QAction类 文件交互QFileDialog类QFileInfo类QFile类QTextStream 绘图QPixmap类QPainter类QBrush类QPen类QPainterPath类 游戏场景QGraphicsItem类QGraphicsScene类QGraphicsView类 窗口设置 QMainWindow类 QMainW…...
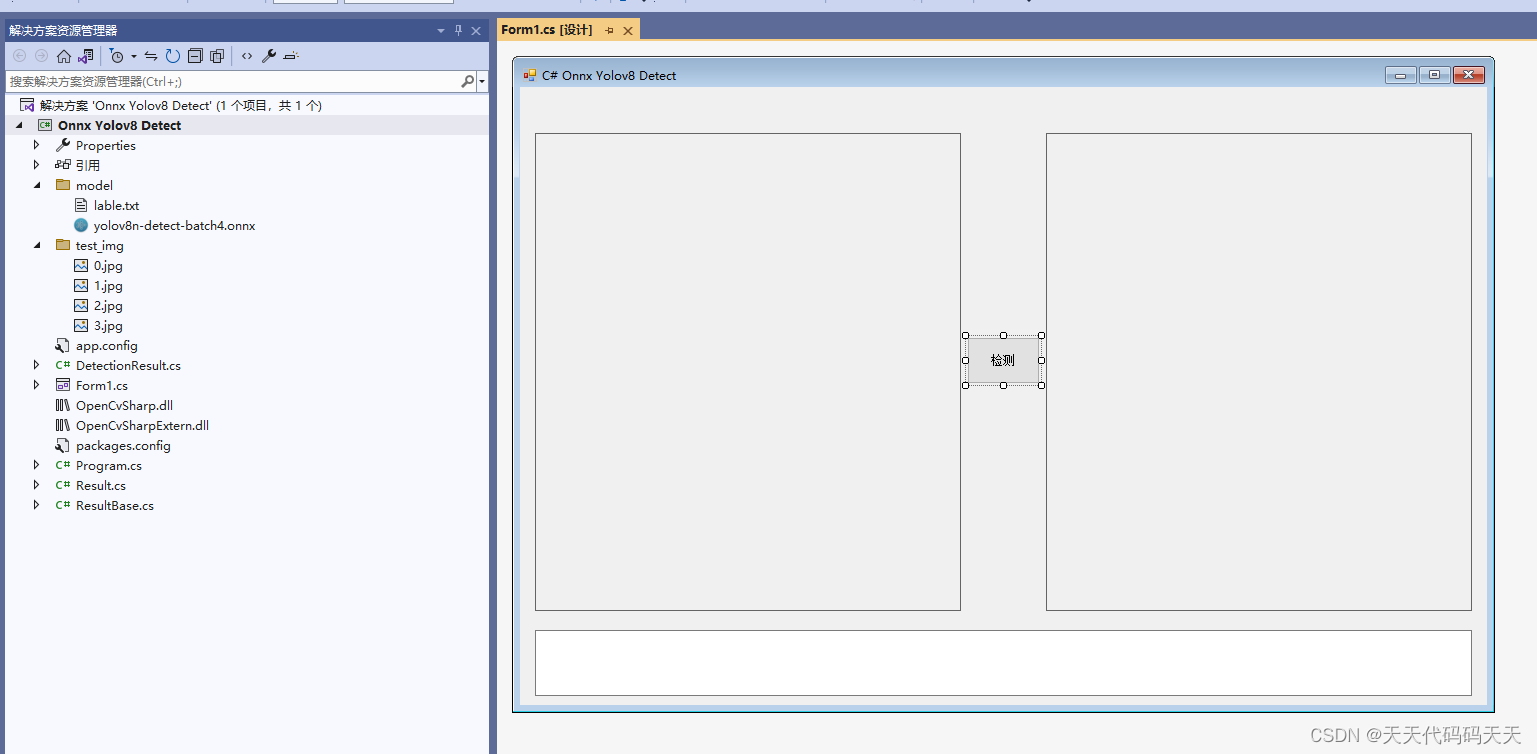
C# Onnx Yolov8 Detect 物体检测 多张图片同时推理
目录 效果 模型信息 项目 代码 下载 C# Onnx Yolov8 Detect 物体检测 多张图片同时推理 效果 模型信息 Model Properties ------------------------- date:2023-12-18T11:47:29.332397 description:Ultralytics YOLOv8n-detect model trained on …...
学习使用js保留两位小数同时去掉小数末尾多余的00
学习使用js保留两位小数同时去掉小数末尾多余的00 前言去除00方法 前言 let number 50000000;let new_number number / 10000;console.log(formatter-new_number, new_number);return new_number.toFixed(2) 万;会发现整数使用toFixed(2),之后会有多余的.00 去…...
linux驱动的学习 驱动开发初识
1 设备的概念 在学习驱动和其开发之前,首先要知道所谓驱动,其对象就是设备。 1.1 主设备号&次设备号: 在Linux中,各种设备都以文件的形式存在/dev目录下,称为设备文件。最上层的应用程序可以打开,关…...

Node.js中npm中ws的WebSocket协议的实现
在Node.js中,ws是一个非常有用的模块,它提供了WebSocket协议的实现。WebSocket协议是一种在Web浏览器和服务器之间进行双向通信的协议,它可以使得Web应用程序更加交互式和实时。在本文中,我们将详细介绍npm中ws的内容。 ws是什么…...

PHP HTTPoxy CGI 应用程序漏洞 CVE-2016-5385
HTTPoxy CGI 应用程序漏洞 CVE-2016-5385 已亲自复现 漏洞名称漏洞描述影响版本 漏洞复现环境搭建漏洞利用 修复建议 漏洞名称 漏洞描述 在Oracle Communications BRM 10.x/12.x(云软件)中发现漏洞。它已经被宣布为关键。此漏洞影响组件用户数据库的未…...
qt-C++笔记之使用QLabel和QPushButton实现一个bool状态的指示灯
qt-C笔记之使用QLabel和QPushButton实现一个bool状态的指示灯 code review! 文章目录 qt-C笔记之使用QLabel和QPushButton实现一个bool状态的指示灯1.QPushButton实现2.QLabel实现2.QLabel实现-对错符号 1.QPushButton实现 运行 代码 #include <QtWidgets>class Ind…...
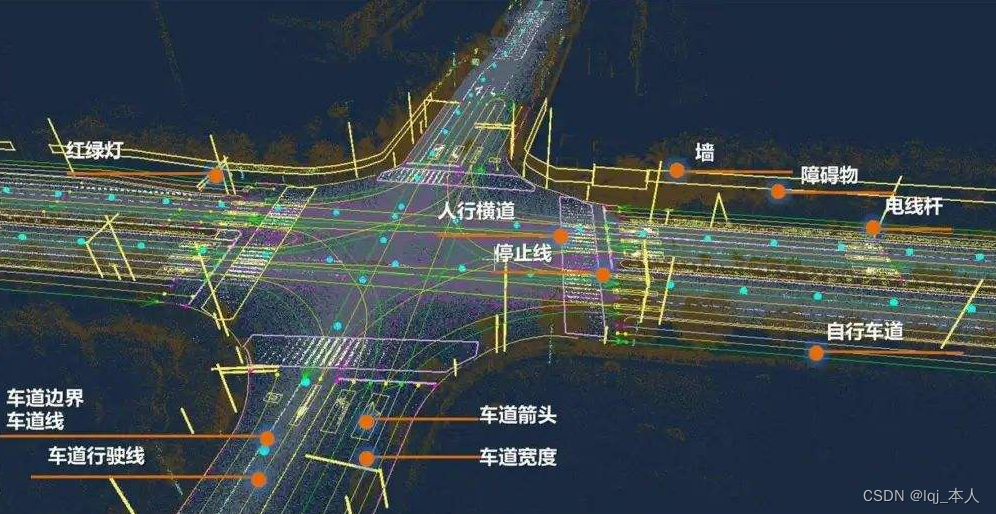
自动驾驶技术入门平台分享:百度Apollo开放平台9.0全方位升级
目录 平台全方位的升级 全新的架构 工具服务 应用软件(场景应用) 软件核心 硬件设备 更强的算法能力 9.0版本算法升级总结 更易用的工程框架 Apollo开放平台9.0版本的技术升级为开发者提供了许多显著的好处,特别是对于深度开发需求…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
