代码随想录 322. 零钱兑换
题目
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
解题思路
本题是完全背包问题,用dp[j]表示组合和为j的最少个数,可以确定递推公式为dp[j]=min(dp[j-coins[i]]+1, dp[j]). 初值dp[0]=0.最后返回dp[amount]。
代码实现
class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount+1,INT_MAX);dp[0] = 0;for (int i=0;i<coins.size();i++) {for (int j=coins[i];j<=amount;j++) {if (dp[j-coins[i]] != INT_MAX) {dp[j] = min(dp[j-coins[i]]+1, dp[j]);}}}if (dp[amount]==INT_MAX) {return -1;}return dp[amount];}
};相关文章:

代码随想录 322. 零钱兑换
题目 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。 你可以认为每种硬币的数量是无限的。…...

【图的应用二:最短路径】- 用 C 语言实现迪杰斯特拉算法和弗洛伊德算法
目录 一、最短路径 二、迪杰斯特拉算法 三、弗洛伊德算法 一、最短路径 假若要在计算机上建立一个交通咨询系统,则可以采用图的结构来表示实际的交通网络。如下图所示,图中顶点表示城市,边表示城市间的交通联系。 这个咨询系统可以回答旅…...
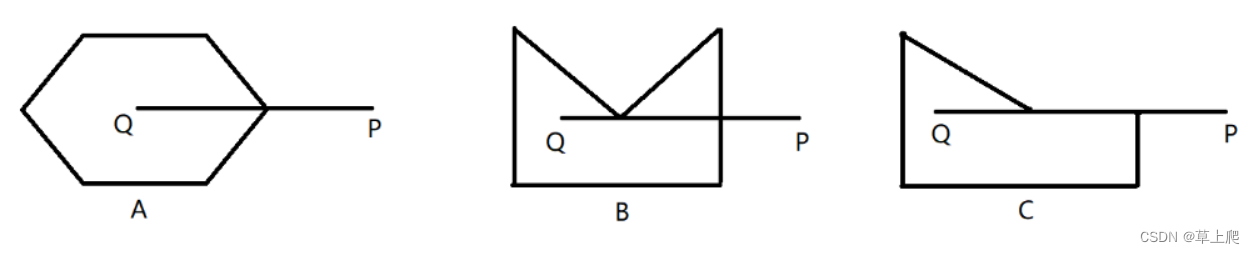
Qt之判断一个点是否在多边形内部(射线法)
算法思想: 以被测点Q为端点,向任意方向作射线(一般水平向右作射线),统计该射线与多边形的交点数。如果为奇数,Q在多边形内;如果为偶数,Q在多边形外。计数的时候会有一些特殊情况。这种方法适用于任意多边形,不需要考虑精度误差和多边形点给出的顺序,时间复杂度为O(n)…...
情况如何解决)
压力测试过程中内存溢出(堆溢出、栈溢出、持久代溢出)情况如何解决
在压力测试过程中,可能会遇到内存溢出的问题,其中常见的包括堆内存溢出、栈内存溢出和持久代溢出。解决这类问题需要首先理解各种内存溢出的原因和特点。 堆内存溢出:这种情况通常发生在稳定性压测一段时间后,系统报错࿰…...

【工业智能】音频信号相关场景
【工业智能】音频信号相关场景 DcaseDcase introduction:dcase2024有10个主题的任务: ASD硬件设备产品商 方法制造业应用场景 zenodo音频事件检测 与计算机视觉CV相对应,计算机听觉computer audition,简称CA。 Dcase 这里推荐一个…...
(PC+WAP)装修设计公司网站模板 家装公司网站源码下载
(PCWAP)装修设计公司网站模板 家装公司网站源码下载 PbootCMS内核开发的网站模板,该模板适用于装修设计、家装公司类等企业,当然其他行业也可以做,只需要把文字图片换成其他行业的即可; PCWAP,同一个后台,…...

使用opencv实现图像中几何图形检测
1 几何图形检测介绍 1.1 轮廓(contours) 什么是轮廓,简单说轮廓就是一些列点相连组成形状、它们拥有同样的颜色、轮廓发现在图像的对象分析、对象检测等方面是非常有用的工具,在OpenCV 中使用轮廓发现相关函数时候要求输入图像是二值图像,这…...

补题与周总结:leetcode第 376 场周赛
文章目录 复盘与一周总结2967. 使数组成为等数数组的最小代价(中位数贪心 回文数判断)2968. 执行操作使频率分数最大(中位数贪心 前缀和 滑窗) 复盘与一周总结 wa穿了第3题,赛时其实想到了思路:中位数贪心…...

js指纹库,可跟踪用户唯一性
fingerprintjs官网 资料: Browserleaks - Check your browser for privacy leaks...

Shell三剑客:awk(内部变量)
一、$0 :完整的输入记录 [rootlocalhost ~]# awk -F: {print $0} passwd.txt root:x:0:0:root:/root:/bin/bash bin:x:1:1:bin:/bin:/sbin/nologin daemon:x:2:2:daemon:/sbin:/sbin/nologin adm:x:3:4:adm:/var/adm:/sbin/nologin lp:x:4:7:lp:/var/spool/lpd:/s…...

JVM中的虚拟机栈的动态链接部分存放到底是什么
在Java虚拟机(JVM)中,每个线程在执行一个方法时都会创建一个栈帧(Stack Frame),栈帧中包含了方法的运行时数据。栈帧通常包括局部变量表、操作数栈、动态链接、方法返回地址等部分。 动态链接 动态链接&a…...
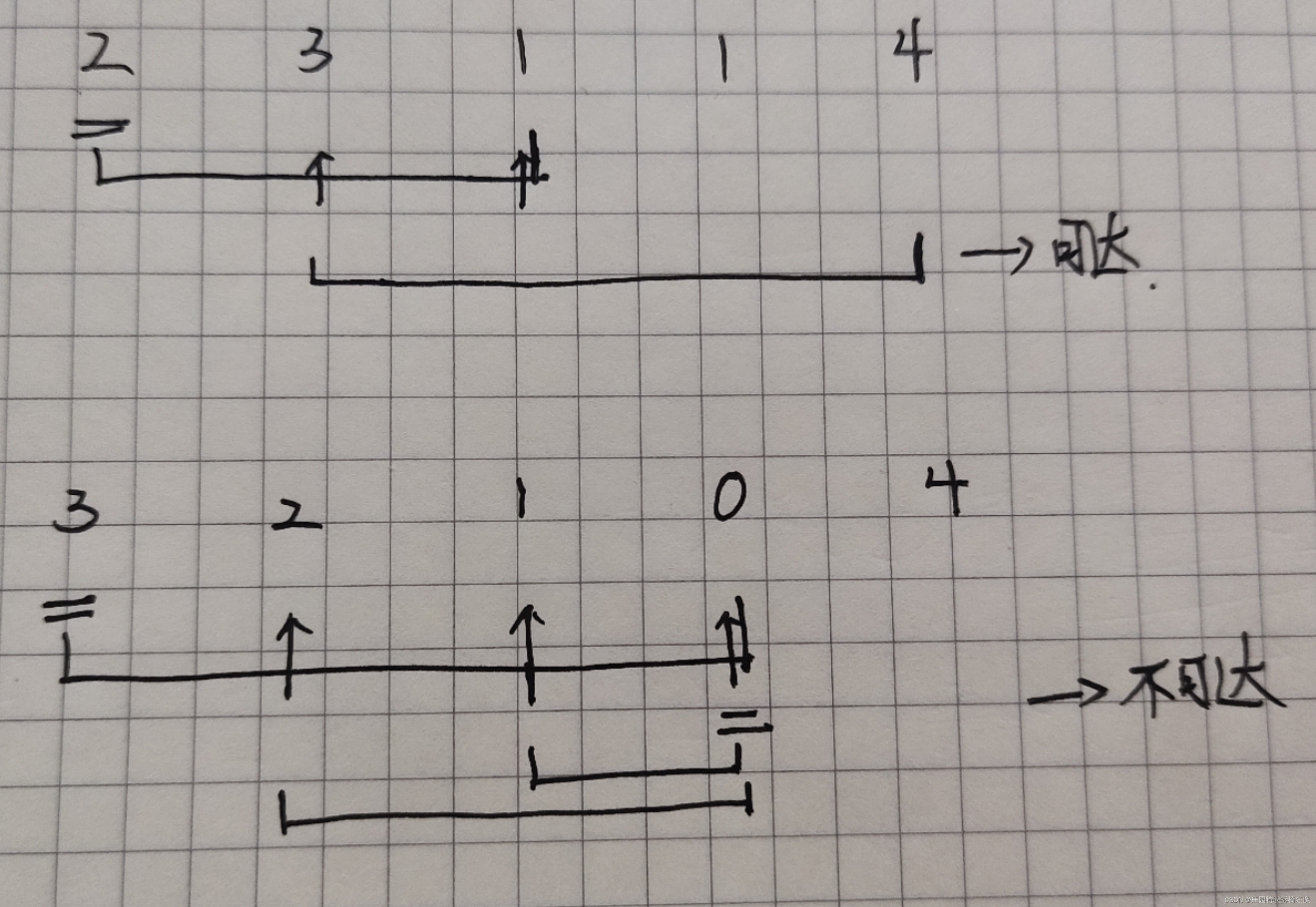
Leetcode 55 跳跃游戏
题意理解: 非负整数数组 nums, 最初位于数组的 第一个下标 。 数组中的每个元素代表你在该位置可以跳跃的最大长度。 需要跳到nums最后一个元素即为成功。 目标:是否能够跳到最后一个元素。 解题思路: 使用贪心算法来解题,需要理解…...

构建陪诊预约系统:技术实战指南
在医疗科技的飞速发展中,陪诊预约系统的应用为患者和陪诊人员提供了更为便捷和贴心的服务。本文将带领您通过技术实现,构建一个简单而实用的陪诊预约系统,以提升医疗服务的效率和用户体验。 技术栈选择 在开始之前,我们需要选择…...

windows和linux将文件删除至回收站【C++】【Go】语言实现
目录 C Windows平台 Linux平台 开平台,代码合并 Go 实现步骤 Go语言实现示例 go单独的windows版本实现 代码解释 C 在C中,将文件移动到回收站的实现在Linux和Windows平台上是不同的。首先,我会为你提供在Windows平台上实现的代码示例…...

10 Vue3中v-html指令的用法
概述 v-html主要是用来渲染富文本内容,比如评论信息,新闻信息,文章信息等。 v-html是一个特别不安全的指令,因为它会将文本以HTML的显示进行渲染,一旦文本里面包含一些恶意的js代码,可能会导致整个网页发…...
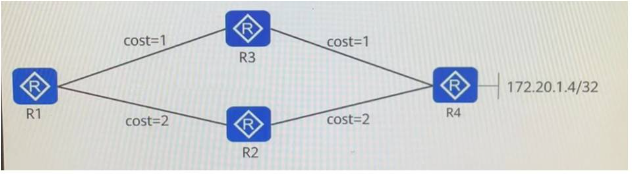
华为数通方向HCIP-DataCom H12-831题库(多选题:181-200)
第181题 如图所示,R1、R2、R3、R4都部署为SPF区域0,链路的cost值如图中标识。R1、R2R3、R4的Loopback0通告入OSPF。R1、R2、R3与R4使用Loopback0作为连接接口,建立BGP对等体关系,其中R4为RR设备,R1、R2、R3是R4的客户端。当R4的直连地址172.20,1,4/32通告入BGP后,以下关R…...
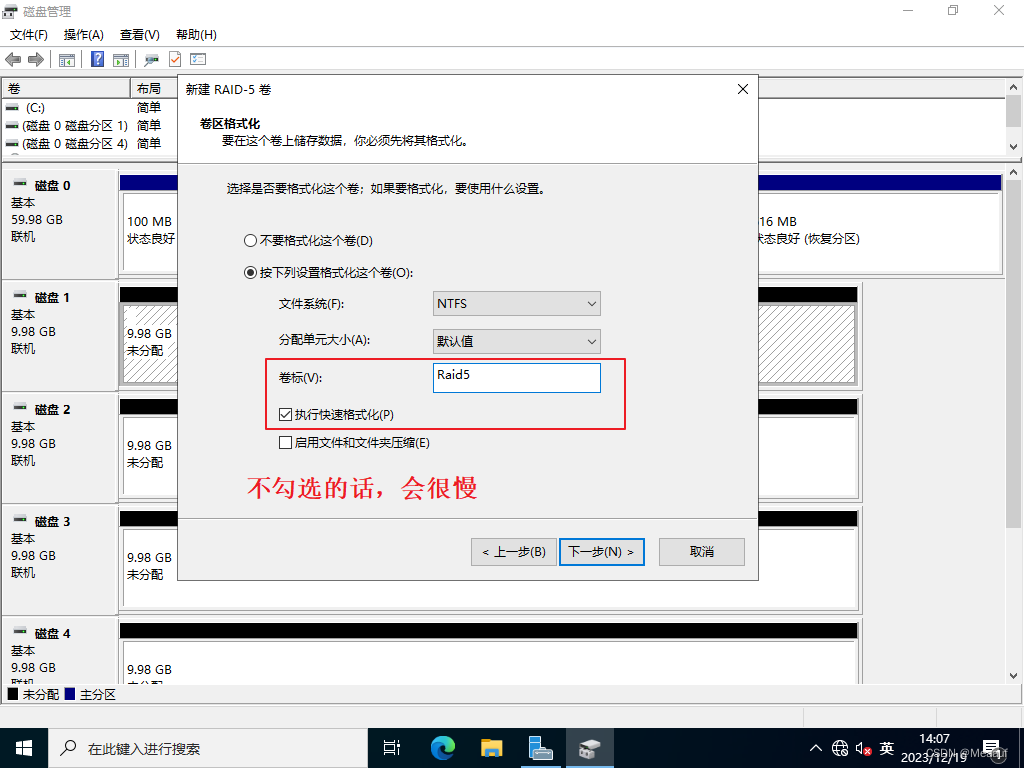
DC-磁盘管理
2023年全国网络系统管理赛项真题 模块B-Windows解析 题目 在DC2上安装及配置软RAID 5。在安装好的DC2虚拟机中添加三块10G虚拟磁盘。组成RAID 5,磁盘分区命名为卷标H盘:Raid5。手动测试破坏一块磁盘,做RAID磁盘修复,确认RAID 5配置完毕。配置步骤 关闭虚拟机,添加3块10G磁…...

使用Docker运行镜像文件与设置端口
1,创建镜像文件前准备 # 使用基础镜像FROM alpine:latest# 设置工作目录WORKDIR /app# 复制应用程序文件到镜像中COPY . .# 暴露容器的端口 不会自动将容器的端口映射到宿主机上 docker run -d -p <宿主机端口>:7080 <镜像名称>EXPOSE 7080# 定义容器启…...

Centos 8.5 Oracle12c安装
由于多次安装踩坑,所以本次写了一份12c安装的完整版。可以直接使用。 一、安装数据库基本信息 名称 值 主机名 database 操作系统 CentOS Linux release 8.5.2111 Oracle用户名/密码 oracle Oracle 版本 12c Enterprise Edition Release 12.2.0.1.0 oracle…...
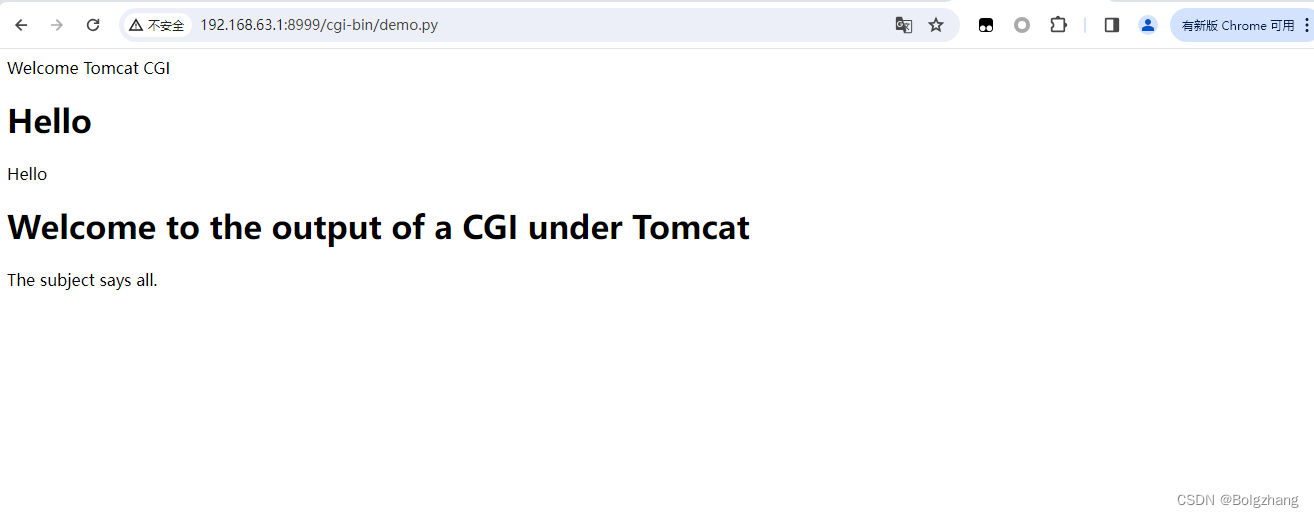
Apache Tomcat httpoxy 安全漏洞 CVE-2016-5388 已亲自复现
Apache Tomcat httpoxy 安全漏洞 CVE-2016-5388 已亲自复现 漏洞名称漏洞描述影响版本 漏洞复现环境搭建漏洞利用 修复建议总结 漏洞名称 漏洞描述 在Apache Tomcat中发现了一个被归类为关键的漏洞,该漏洞在8.5.4(Application Server Soft ware)以下。受影响的是组…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
