【面试题】在JS循环中使用await会怎么样?
前言
这个问题是这样产生的?某天,在学习异步的知识遇到这样一道题:使用Promise的方式,每隔一秒输出数组中一个值
const arr = [1, 2, 3]
arr.reduce((pre, cur) => {return pre.then(() => {returnnewPromise((resolve, reject) => {setTimeout(() => {resolve(console.log(cur))}, 1000);})})
}, Promise.resolve())
复制代码那这段代码还是挺好了解的,相当于
Promise.resolve().then(() => {returnnewPromise((resolve, reject) => {setTimeout(() => {resolve(console.log(1))}, 1000);})
}).then(() => {returnnewPromise((resolve, reject) => {setTimeout(() => {resolve(console.log(2))}, 1000);})
}).then(() => {returnnewPromise((resolve, reject) => {setTimeout(() => {resolve(console.log(3))}, 1000);})
})
复制代码看完之后,我就在想,如果我在循环中,每次输出值之后停止一秒,也可以解决,于是乎就有了以下代码
const arr = [1, 2, 3]
constsleep = (ms) => {returnnewPromise((resolve, reject) => {setTimeout(() => {resolve()}, ms)})
}
for (let i = 0; i < arr.length; i++) {console.log(arr[i]);awaitsleep(1000)
}
复制代码打印结果也是符合预期的,在这里我就产生了第一个疑问:await不是要搭配async使用的么?这里怎么能单独使用?(不信你把代码放到浏览器控制台试试)
接着我把for改成了forEach,发现根本达不到效果,第二个疑问产生:forEach中await为什么失效了呢?
arr.forEach(async item => {console.log(item);await sleep(1000)
})
复制代码带着这两个疑问,那就开始学习起来,寻找答案。
在for循环中的await
记得在学习async/await的时候有这样一句话,await只能和async搭配一起使用,其实这句话是没有错的。那为什么前面可以直接写await呢,因为我是直接写在浏览器控制台的,咱们在编辑器写代码的时候一定要套一个async使用的
<script> const arr = [1, 2, 3]constsleep = (ms) => {returnnewPromise((resolve, reject) => {setTimeout(() => {resolve()}, ms)})}constlogByOneSecond = async () => {for (let i = 0; i < arr.length; i++) {console.log(arr[i]);awaitsleep(1000)}} logByOneSecond()</script>
复制代码所以这就算闹了个笑话,哈哈,不过当我遇到不理解的时候,又多了一个思考方向。
好的,如上所述,await确实发挥了他的作用,让JS直到等到了promise返回的处理结果,再继续往下执行;那for...of,while是不是也可以呢
const logByForof = async () => {for (const item of arr) {console.log(item);await sleep(1000)}
}
logByForof()
复制代码constlogByWhile = async () => {let i = 0while (i !== arr.length) {awaitsleep(1000)console.log(arr[i]);i++}
}
logByWhile()
复制代码结果也是符合预期,可以在循环中使用await并实现效果
在forEach循环中的await
如一开始,在forEach中并没有的到预期的效果;首先得到一个结果:forEach中async 和await是无效的。
那我看到的解释有以下几种
JavaScript 中的 forEach不支持 promise 感知,也不支持 async 和await,所以不能在 forEach 使用 await 。
map/forEach内部使用了while结合callback方式来执行函数,await不会等待callback的执行
forEach 只支持同步代码
第二种说法,简化以后的伪代码,如下
while(index < arr.length){callback(item, index)
}
复制代码map/forEach是简单的执行下回调函数,并不会处理异步的情况。即:map/forEach 会同时创建出多个回调函数,多个回调函数被加上了各自的 async、await,如下
async ()=>{await sleep(1000);
}
async ()=>{ await sleep(1000);
}
async ()=>{ await sleep(1000);
}
复制代码各个函数之间是独立的,彼此的回调也是独立的;请求是异步的,彼此之间又没有关联,顺序也就自然无法保证
总结
回顾了 async/await 在循环语句里的使用方法,对于普通的 for-loop,所有的 await 都是串行调用的,可以放心使用,包括 while、for-in、for-of 等等;但是在有 callback 的 array 方法,如 forEach、map、filter、reduce 等等,有许多副作用,最好就别使用 await 了。
大厂面试题分享 面试题库
前端后端面试题库 (面试必备) 推荐:★★★★★
地址:前端面试题库
相关文章:

【面试题】在JS循环中使用await会怎么样?
前言这个问题是这样产生的?某天,在学习异步的知识遇到这样一道题:使用Promise的方式,每隔一秒输出数组中一个值const arr [1, 2, 3] arr.reduce((pre, cur) > {return pre.then(() > {returnnewPromise((resolve, rejec…...

Qt QMessageBox详解
文章目录一.QMessageBox介绍枚举属性函数二.QMessageBox的用法1.导入QMessage库2.弹窗提示3.提供选项的弹窗提示4.作为提示,报警,报错提示窗口一.QMessageBox介绍 文本消息显示框(message box)向用户发出情况警报信息并进一步解释警报或向用户提问&…...

Flutter之beamer路由入门指南
beamer路由入门指南 前言使用方法1、路由配置方式1路由配置方式2路由跳转测试现象前言 Beamer是一个很好用的路由组件,本文以beamer1.5.0版本进行说明,前面博主也介绍了其他路由组件 Flutter实战之go_router路由组件入门指南 、 Flutter之Fluro路由组件入门指南 Flutter之Ge…...

「基础篇」机器学习概览
文章目录1. 什么是机器学习2. 引入机器学习3. 应用场景4. 机器学习分类4.1. 有无人类监督4.2. 是否增量学习4.3. 泛化方式5. 主要挑战6. 测试与验证1. 什么是机器学习 机器学习(Machine Learning,ML)是一个研究领域,让计算机无需…...
揭秘可视化图探索工具 NebulaGraph Explore 是如何实现图计算的
前言 在可视化图探索工具 NebulaGraph Explorer 3.1.0 版本中加入了图计算工作流功能,针对 NebulaGraph 提供了图计算的能力,同时可以利用工作流的 nGQL 运行能力支持简单的数据读取,过滤及写入等数据处理功能。 本文将简单分享下 NebulaGr…...
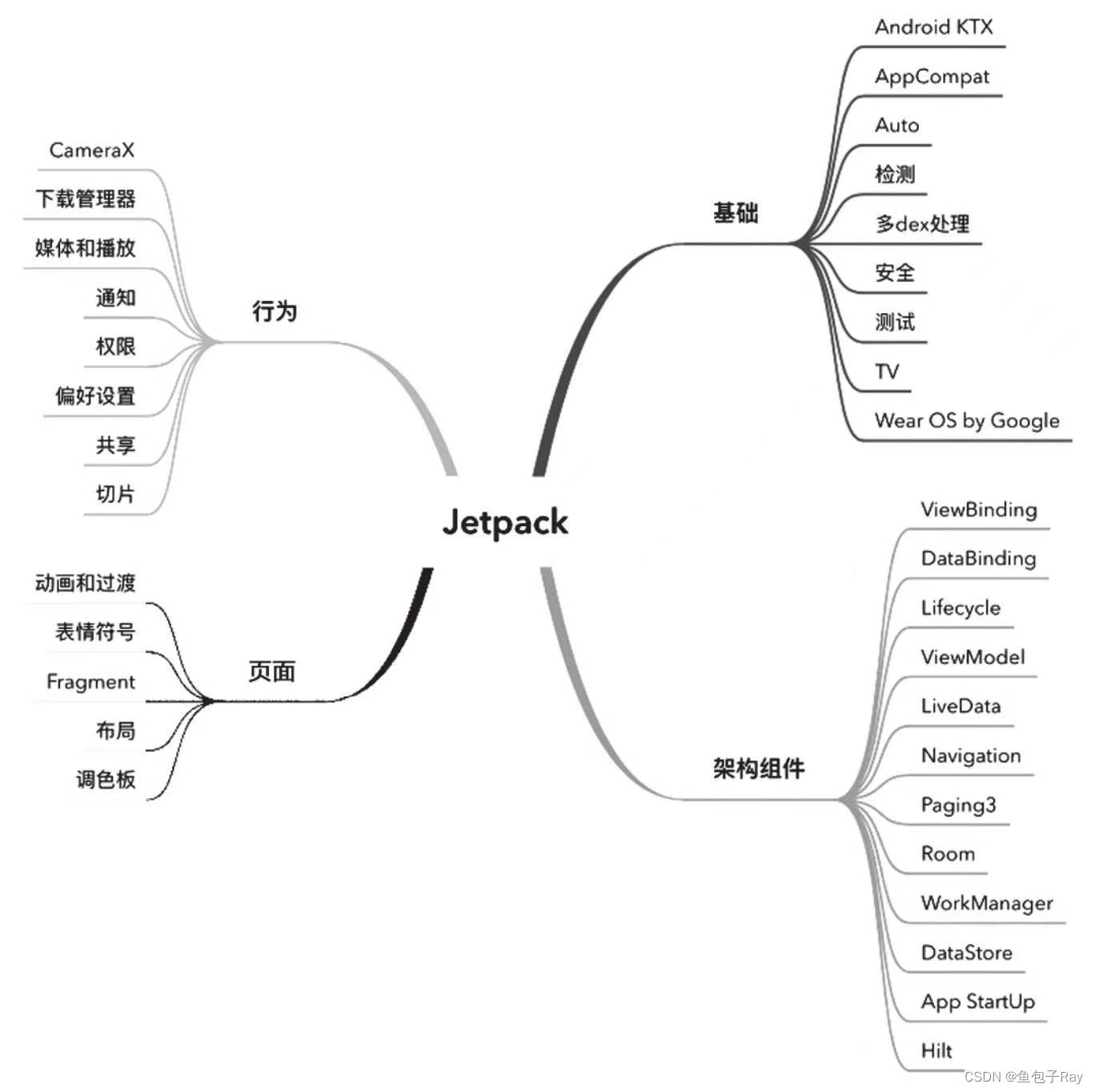
移动架构43_什么是Jetpack
Android移动架构汇总 文章目录一 Android 开发框架演变1 MVC2 MVP3 MVVM二 什么是JetPack三 如何构建支持Jetpack项目一 Android 开发框架演变 1 MVC Model-View-Controller,模型-视图-控制器,Model负责数据管理,View负责UI显…...

TiDB的分布式事务原理探究
事务开启 获取全局授时作为startTS构建一个tikvTxn对象(包括snapshot)。 事务写 txn.Set方法本质上将kv值写入了一个内存缓存(即kv/memdb_buffer.go中的memDbBuffer)中。该内存kv数据库利用的是golevel提供的功能。 事务回滚 直接将tikvTxn的valid字段…...

【C语言】函数指针和指针函数
文章目录[TOC](文章目录)前言概述函数指针定义:使用:回调函数指针函数前言 今天学一下函数指针 提示:以下是本篇文章正文内容,下面案例可供参考 概述 函数指针:是一个指向函数的指针,在内存空间中存放的…...

Nodejs中npx简介和作用
一、npx简介npm从5.25.2版开始,增加了 npx 命令。方便了我在项目中使用全局包。二、安装Node安装后自带npm模块,可以直接使用npx命令。如果不能使用用,就要手动安装一下。npm install -g npx三、使用npx想要解决的主要问题,就是调…...
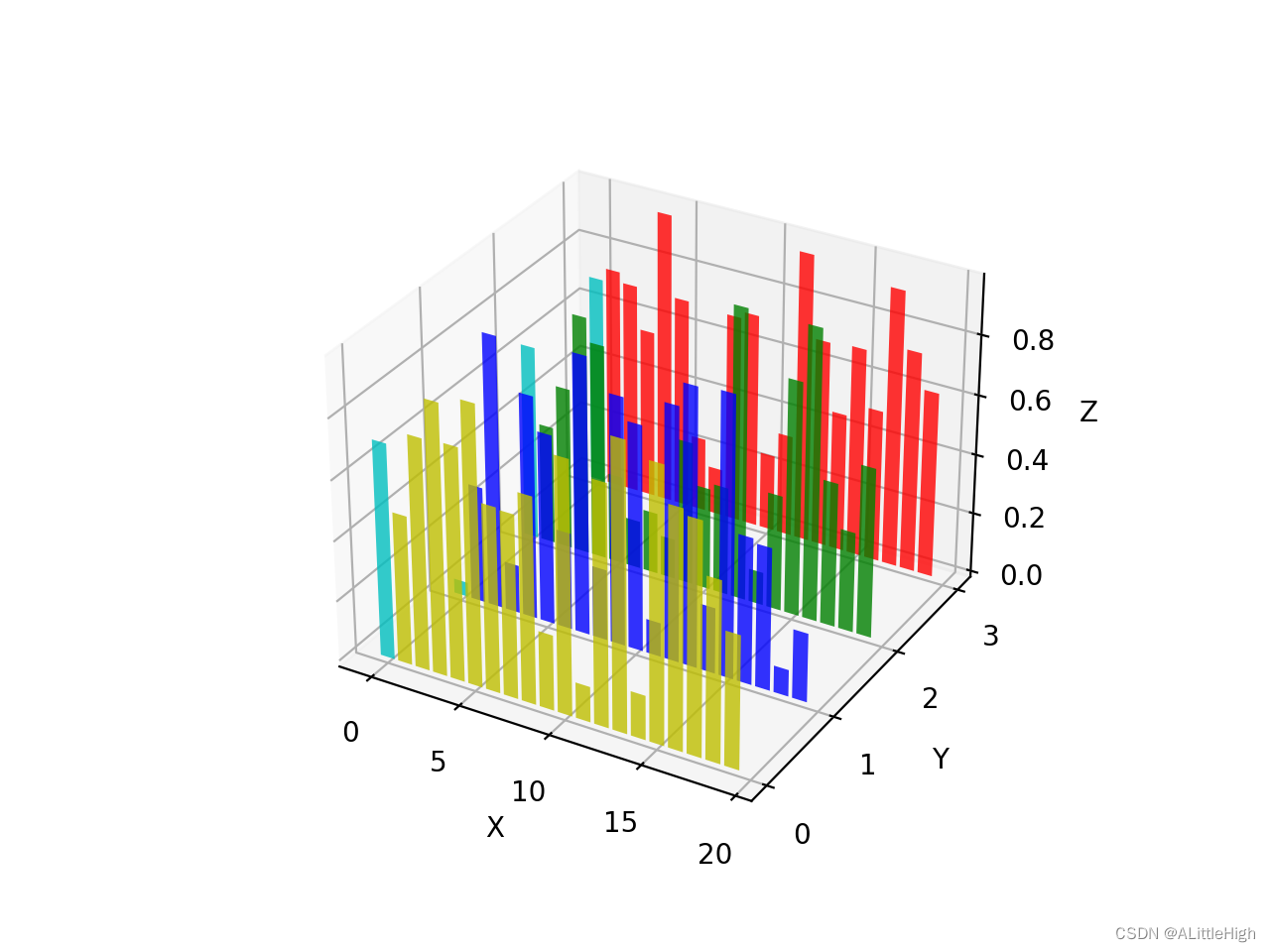
Matplotlib精品学习笔记001——绘制3D图形详解+实例讲解
3D图片更生动,或许在时间序列数据的展示上更胜一筹 想法: 学习3D绘图的想法来自科研绘图中。我从事的专业是古植物学,也就是和植物化石打交道。化石有三大信息:1.物种信息,也就是它的分类学价值;2.时间信息…...

学习ifconfig实战技巧,成为网络管理高手
文章目录前言一. ifconfig 命令介绍二. 语法格式及常用选项三. 参考案例3.1 显示网络设备信息3.2 启动和关闭指定的网卡3.3 对指定的网卡设备执行修改IP地址操作3.4 启动和关闭ARP协议3.5 使用ifconfig添加网卡总结前言 大家好,又见面了,我是沐风晓月&a…...
、322. 零钱兑换、279.完全平方数)
day38|70. 爬楼梯(进阶)、322. 零钱兑换、279.完全平方数
70. 爬楼梯(进阶) 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 示例 1: 输入:n 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 1 阶 2. 2…...
SpringBoot全局异常处理
一、目的 当客户端/前端向服务端发送一个请求后,这个请求并不是每次都能完全正确的处理,比如出现一些资源不存在、参数错误或者内部错误等信息的时候,就需要将异常反馈给客户端或者前端。那么这就需要程序有完整的异常处理机制。 在 Java 中所…...

SpringBoot异常处理
目录 一、 错误处理 1. 默认规则 2. 定制错误处理逻辑 二、自定义异常处理 1. 实现 ErrorController 2. RestControllerAdvice/ControllerAdvice ExceptionHandler 实现自定义异常 3. 新建 UserController.class 测试 3 种不同异常的处理 4. 最终效果如下 补充 1. 参…...
《C++ Primer Plus》(第6版)第8章编程练习
《C Primer Plus》(第6版)第8章编程练习《C Primer Plus》(第6版)第8章编程练习1. 打印字符串2. CandyBar3. 将string对象的内容转换为大写4. 设置并打印字符串5. max5()6. maxn()7. SumArray()《C Primer Plus》(第6版…...

RAD Studio 11.3 Alexandria Crack
RAD Studio 11.3 Alexandria Crack 瞄准最新平台版本-此版本增加了对Android 13和Apple macOS Ventura的官方支持。它还支持Ubuntu 22 LTS和Microsoft Windows Server 2022。 使用生物特征认证-New为FireMonkey移动应用程序提供了新的移动生物特征认证组件。 部署嵌入式InterBa…...

Stm32 iic 协议使用
/* 第1个参数为I2C操作句柄 第2个参数为从机设备地址 第3个参数为从机寄存器地址 第4个参数为从机寄存器地址长度 第5个参数为发送的数据的起始地址 第6个参数为传输数据的大小 第7个参数为操作超时时间 */ HAL_I2C_Mem_Write(&hi2c2,salve_add,0,0,PA_BUFF,sizeof(PA_BUFF…...
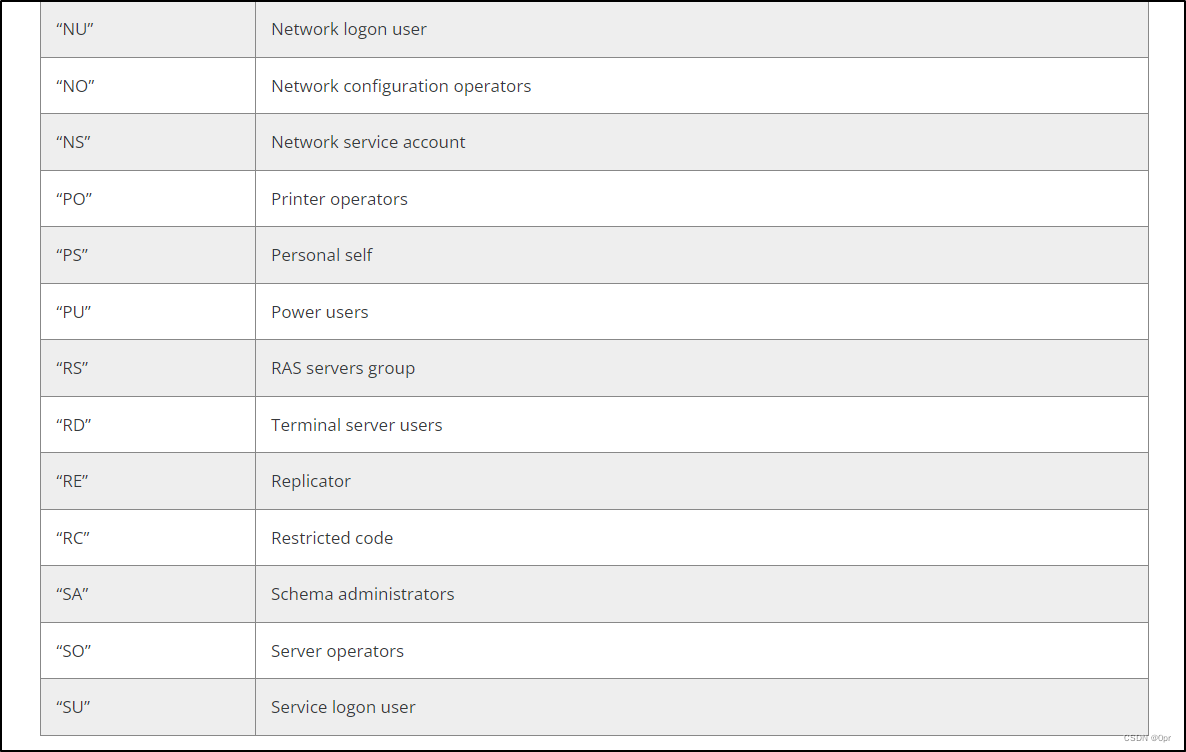
Malware Dev 02 - Windows SDDL 后门利用之 SCManager
写在最前 如果你是信息安全爱好者,如果你想考一些证书来提升自己的能力,那么欢迎大家来我的 Discord 频道 Northern Bay。邀请链接在这里: https://discord.gg/9XvvuFq9Wb我拥有 OSCP,OSEP,OSWE,OSED&…...

每日一题29——山峰数组的顶部
符合下列属性的数组 arr 称为 山峰数组(山脉数组) : arr.length > 3 存在 i(0 < i < arr.length - 1)使得: arr[0] < arr[1] < ... arr[i-1] < arr[i] arr[i] > arr[i1] > ... &g…...

Linux- 系统随你玩之--好用到炸裂的系统级监控、诊断工具
文章目录1、前言2、lsof介绍2.1、问题来了: 所有用户都可以采用该命令吗?3、 服务器安装lsof3.1、安装3.2、检查安装是否正常。4、lsof 命令4.1、常用功能选项4.2、输出内容4.2.1 、FD和 TYPE列5、 lsof 命令实操常见用法6 、常用组合命令7、 结语1、前言…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
