【C语言】函数指针和指针函数
文章目录
- @[TOC](文章目录)
- 前言
- 概述
- 函数指针
- 定义:
- 使用:
- 回调函数
- 指针函数
文章目录
- @[TOC](文章目录)
- 前言
- 概述
- 函数指针
- 定义:
- 使用:
- 回调函数
- 指针函数
前言
今天学一下函数指针
提示:以下是本篇文章正文内容,下面案例可供参考
概述
函数指针:是一个指向函数的指针,在内存空间中存放的是函数的地址。

parr是一个指向数组的指针,它存放的是数组的地址
数组指针–存放数组地址的指针
&数组名–得到数组地址
==函数指针–存放函数地址的指针
&函数名–得到函数地址
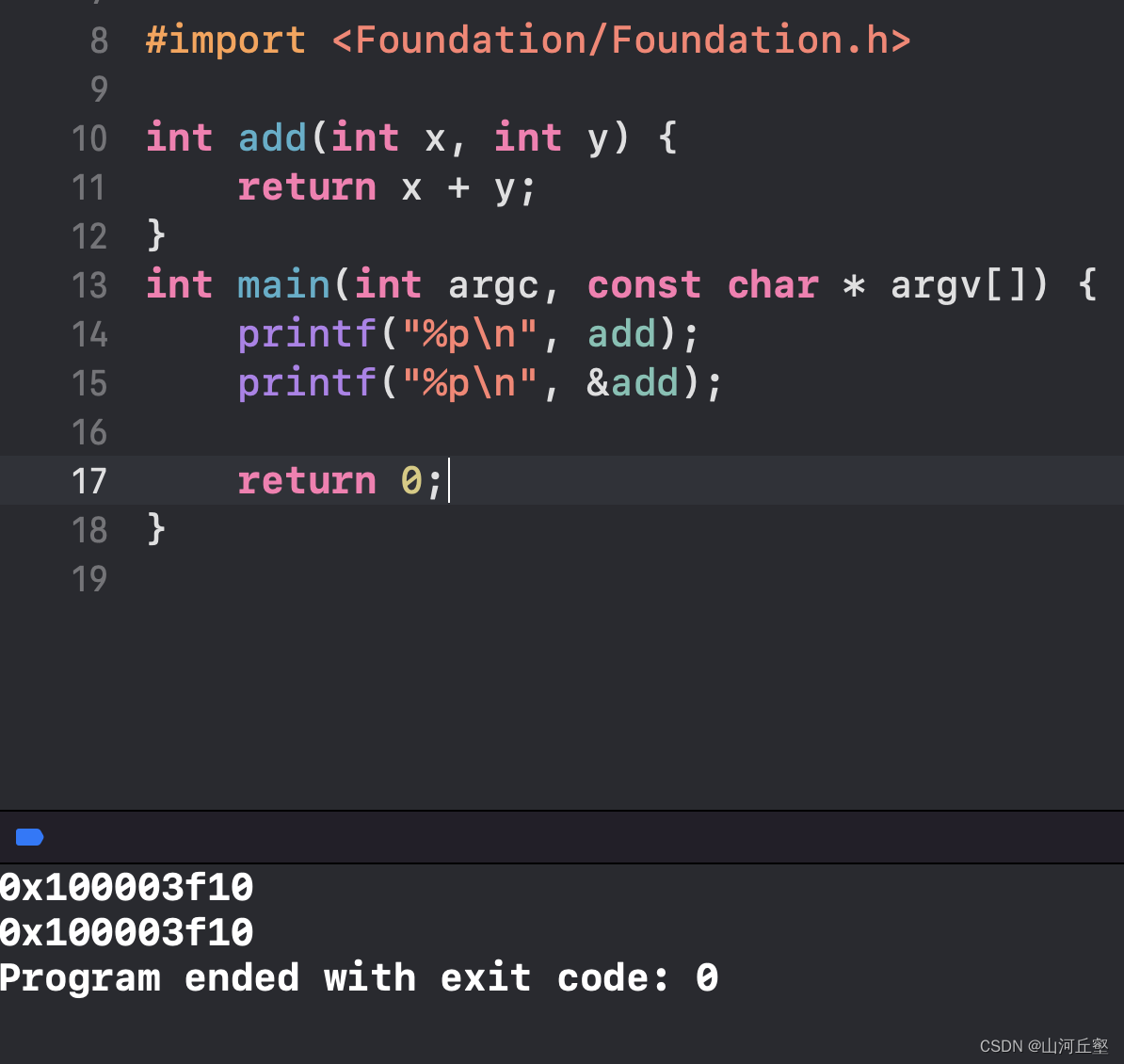
函数指针
定义:
函数指针的本质是一个指针,该指针的地址指向了一个函数,所以它是指向函数的指针。
声明形式:
ret (*p)(args,....)
函数指针:函数的返回值类型(*指针名)(函数的参数列表类型)
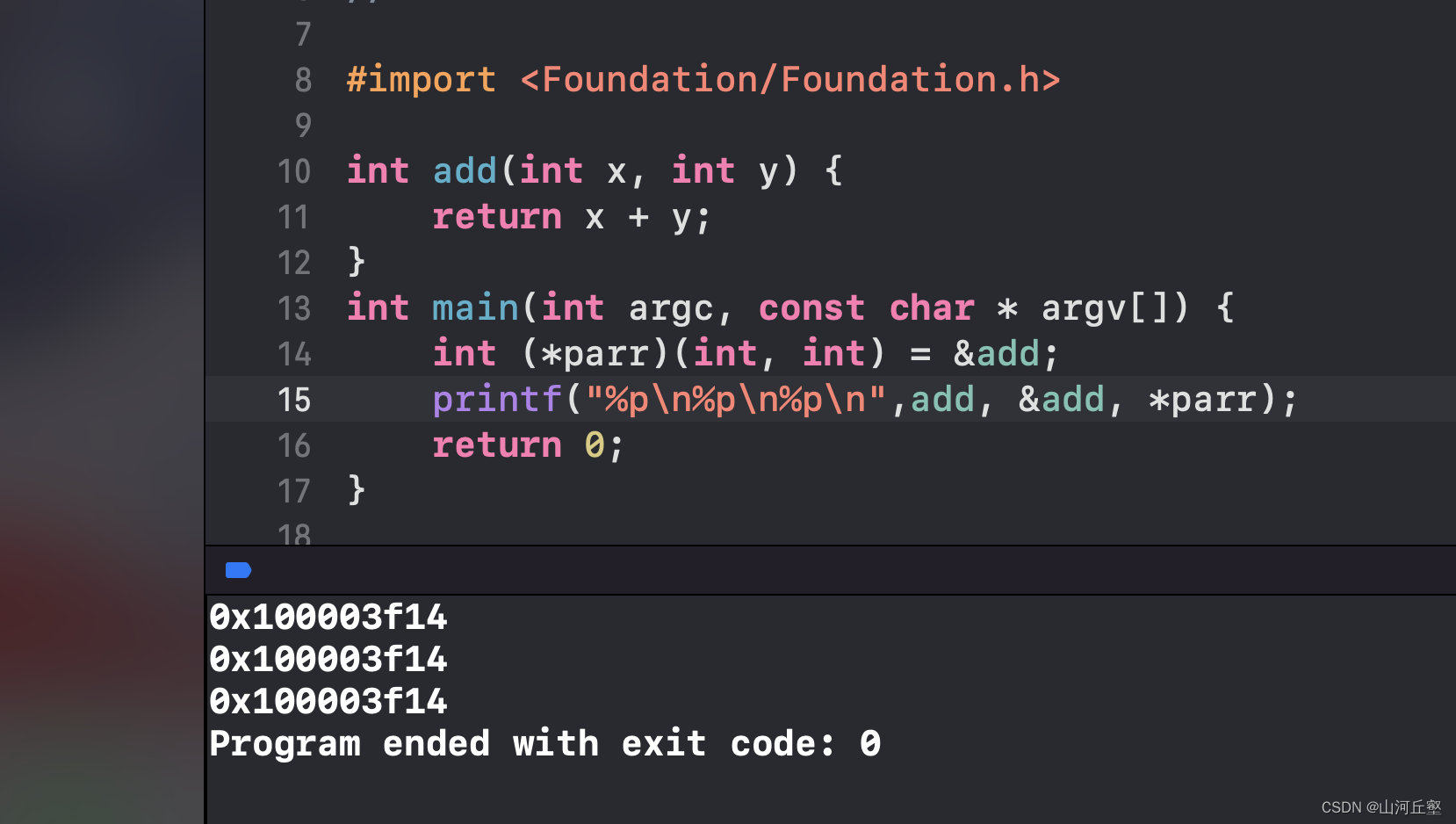
使用:
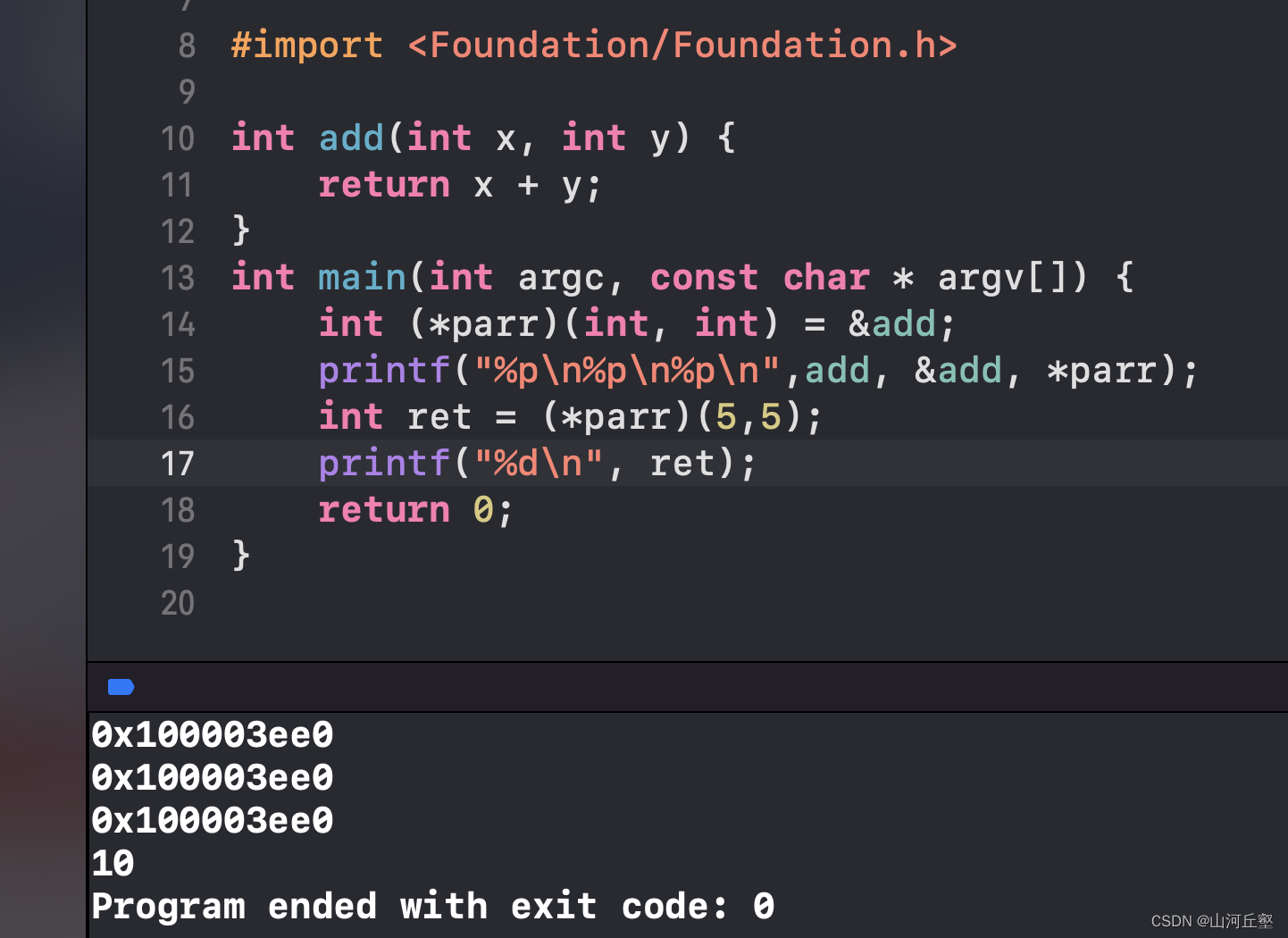
- int ret = (*parr)(5,5);
- 函数名=&函数名
- “ int (*parr)(int, int) = &add; ” = “int (*parr)(int, int) = add;”
- “ int ret = (*parr)(5,5);” = “int ret = parr(5,5); ” = "int ret = add(5,5)”
- 对于int ret = (*parr)(5,5)来说,*是没有意义的。有没有结果都一样
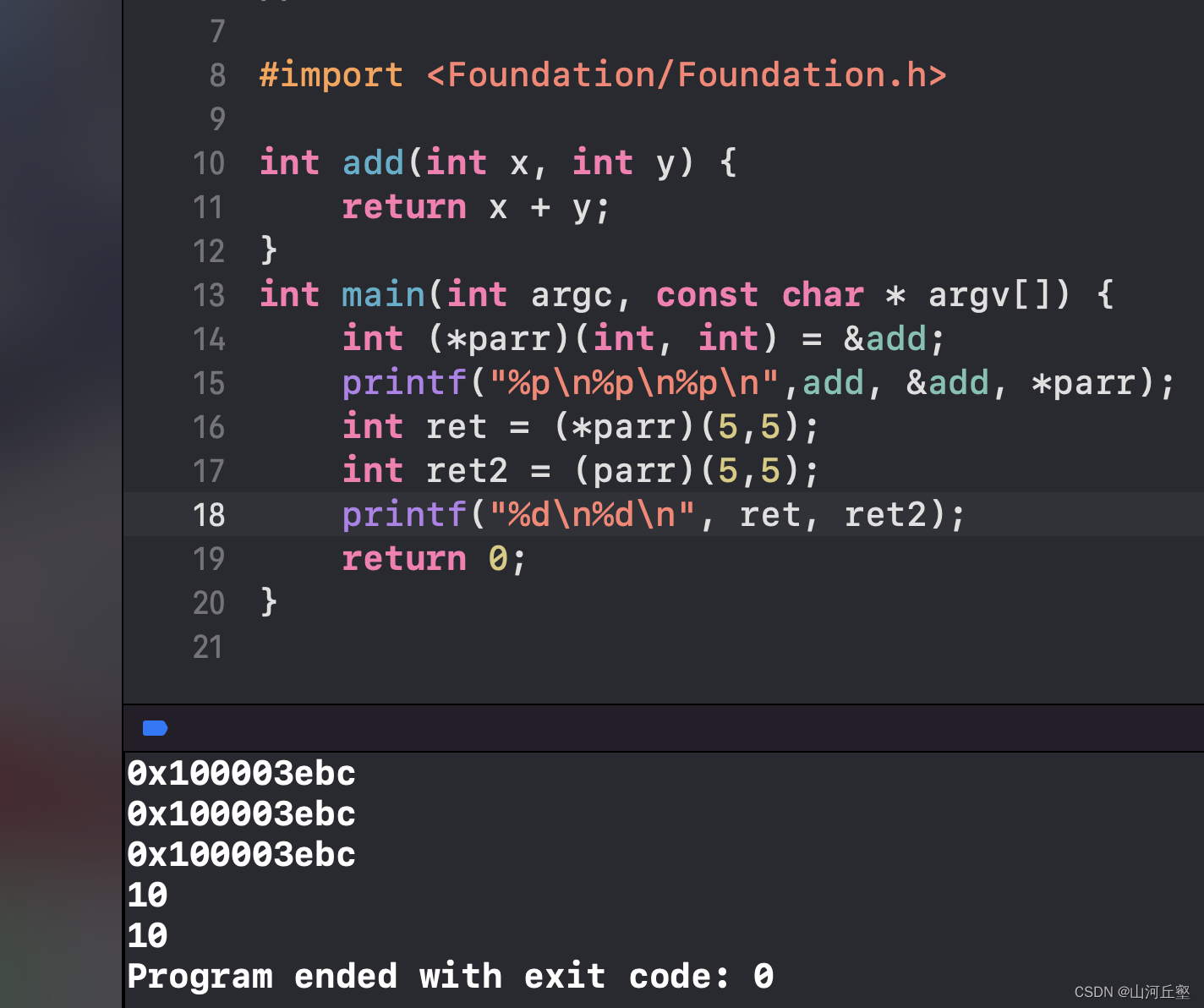
回调函数
回调函数就是一个通过指针函数调用的函数,将其函数指针作为参数传给另一个函数。回调函数是在特定的事件发生时由另外一方调用的。
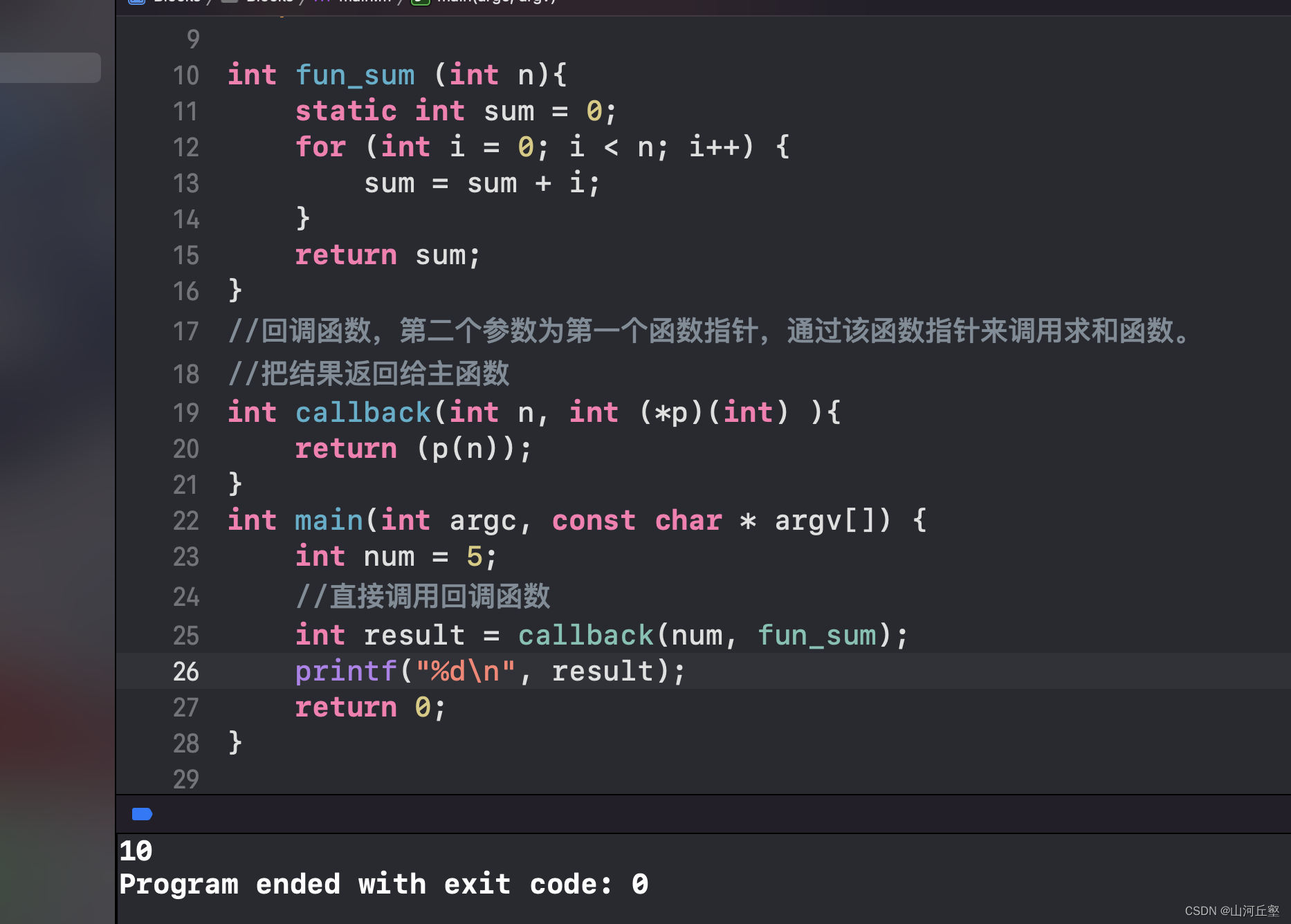
指针函数
指针函数的本质是一个函数,他的返回值是一个指针。
声明形式:
ret *fun(args,....)
在使用指针函数的时候,需要避免返回局部变量指针的情况

一般的变量是存储在栈区的,当函数结束,栈区的变量就会被释放,如果我们在函数内部定义一个变量,在使用一个指针去指向这个变量,当函数调用结束时,这个变量可能就会被释放,九三返回了该地址的指针,也不一定能得到正确的值。
如果我们使用static修饰变量,(上面的static sum)那么该变量就变为了静态变量,静态变量是存放在数据段的,他的生命周期存在于整个程序运行期间。只要程序没有结束,该变量就一直存在。
还有一种解决方法是使用全局变量。因为全局变量也是存放于数据段的。
相关文章:

【C语言】函数指针和指针函数
文章目录[TOC](文章目录)前言概述函数指针定义:使用:回调函数指针函数前言 今天学一下函数指针 提示:以下是本篇文章正文内容,下面案例可供参考 概述 函数指针:是一个指向函数的指针,在内存空间中存放的…...

Nodejs中npx简介和作用
一、npx简介npm从5.25.2版开始,增加了 npx 命令。方便了我在项目中使用全局包。二、安装Node安装后自带npm模块,可以直接使用npx命令。如果不能使用用,就要手动安装一下。npm install -g npx三、使用npx想要解决的主要问题,就是调…...
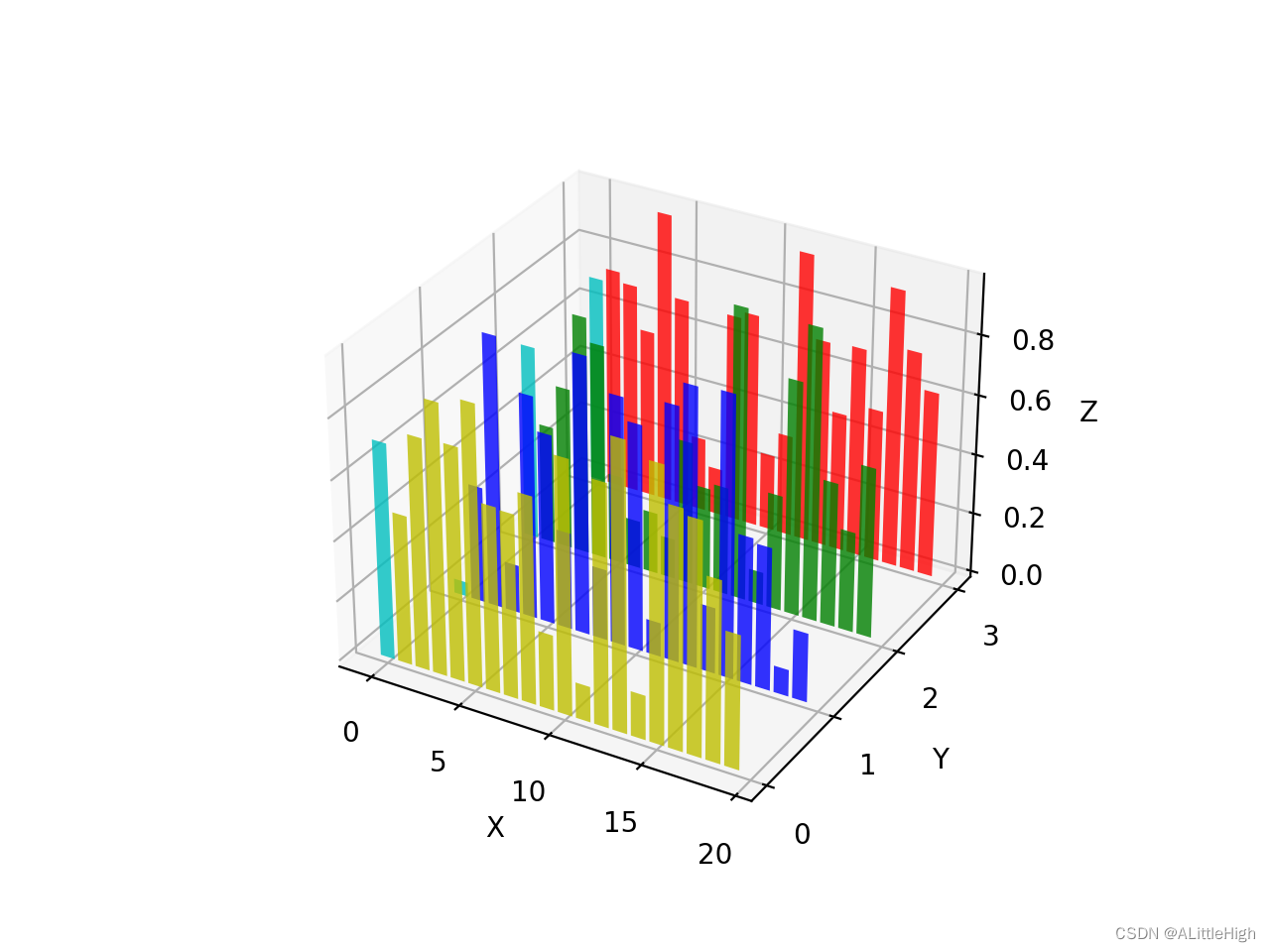
Matplotlib精品学习笔记001——绘制3D图形详解+实例讲解
3D图片更生动,或许在时间序列数据的展示上更胜一筹 想法: 学习3D绘图的想法来自科研绘图中。我从事的专业是古植物学,也就是和植物化石打交道。化石有三大信息:1.物种信息,也就是它的分类学价值;2.时间信息…...

学习ifconfig实战技巧,成为网络管理高手
文章目录前言一. ifconfig 命令介绍二. 语法格式及常用选项三. 参考案例3.1 显示网络设备信息3.2 启动和关闭指定的网卡3.3 对指定的网卡设备执行修改IP地址操作3.4 启动和关闭ARP协议3.5 使用ifconfig添加网卡总结前言 大家好,又见面了,我是沐风晓月&a…...
、322. 零钱兑换、279.完全平方数)
day38|70. 爬楼梯(进阶)、322. 零钱兑换、279.完全平方数
70. 爬楼梯(进阶) 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 示例 1: 输入:n 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 1 阶 2. 2…...
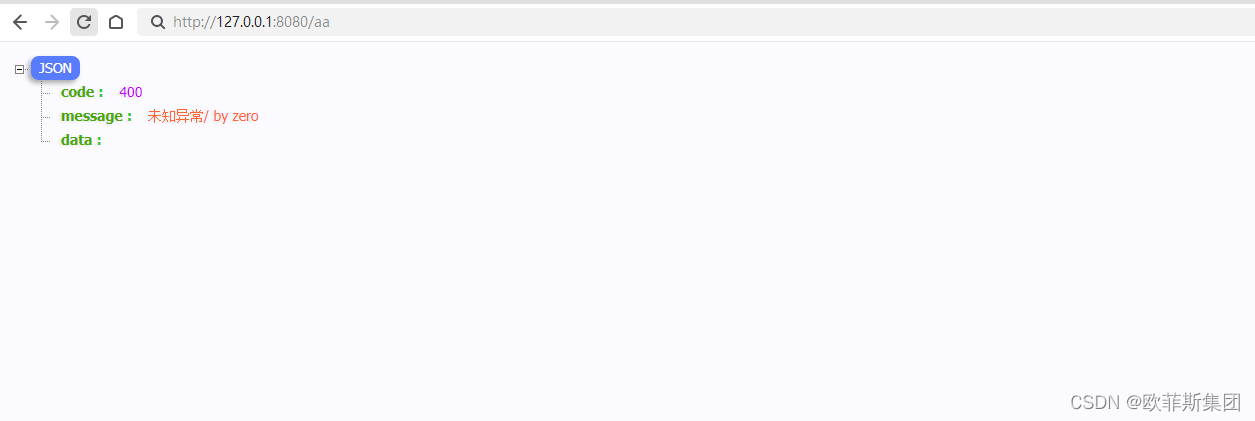
SpringBoot全局异常处理
一、目的 当客户端/前端向服务端发送一个请求后,这个请求并不是每次都能完全正确的处理,比如出现一些资源不存在、参数错误或者内部错误等信息的时候,就需要将异常反馈给客户端或者前端。那么这就需要程序有完整的异常处理机制。 在 Java 中所…...

SpringBoot异常处理
目录 一、 错误处理 1. 默认规则 2. 定制错误处理逻辑 二、自定义异常处理 1. 实现 ErrorController 2. RestControllerAdvice/ControllerAdvice ExceptionHandler 实现自定义异常 3. 新建 UserController.class 测试 3 种不同异常的处理 4. 最终效果如下 补充 1. 参…...
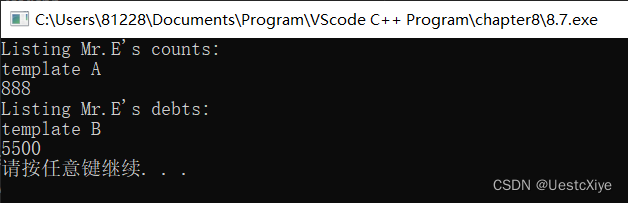
《C++ Primer Plus》(第6版)第8章编程练习
《C Primer Plus》(第6版)第8章编程练习《C Primer Plus》(第6版)第8章编程练习1. 打印字符串2. CandyBar3. 将string对象的内容转换为大写4. 设置并打印字符串5. max5()6. maxn()7. SumArray()《C Primer Plus》(第6版…...

RAD Studio 11.3 Alexandria Crack
RAD Studio 11.3 Alexandria Crack 瞄准最新平台版本-此版本增加了对Android 13和Apple macOS Ventura的官方支持。它还支持Ubuntu 22 LTS和Microsoft Windows Server 2022。 使用生物特征认证-New为FireMonkey移动应用程序提供了新的移动生物特征认证组件。 部署嵌入式InterBa…...

Stm32 iic 协议使用
/* 第1个参数为I2C操作句柄 第2个参数为从机设备地址 第3个参数为从机寄存器地址 第4个参数为从机寄存器地址长度 第5个参数为发送的数据的起始地址 第6个参数为传输数据的大小 第7个参数为操作超时时间 */ HAL_I2C_Mem_Write(&hi2c2,salve_add,0,0,PA_BUFF,sizeof(PA_BUFF…...
Malware Dev 02 - Windows SDDL 后门利用之 SCManager
写在最前 如果你是信息安全爱好者,如果你想考一些证书来提升自己的能力,那么欢迎大家来我的 Discord 频道 Northern Bay。邀请链接在这里: https://discord.gg/9XvvuFq9Wb我拥有 OSCP,OSEP,OSWE,OSED&…...

每日一题29——山峰数组的顶部
符合下列属性的数组 arr 称为 山峰数组(山脉数组) : arr.length > 3 存在 i(0 < i < arr.length - 1)使得: arr[0] < arr[1] < ... arr[i-1] < arr[i] arr[i] > arr[i1] > ... &g…...

Linux- 系统随你玩之--好用到炸裂的系统级监控、诊断工具
文章目录1、前言2、lsof介绍2.1、问题来了: 所有用户都可以采用该命令吗?3、 服务器安装lsof3.1、安装3.2、检查安装是否正常。4、lsof 命令4.1、常用功能选项4.2、输出内容4.2.1 、FD和 TYPE列5、 lsof 命令实操常见用法6 、常用组合命令7、 结语1、前言…...
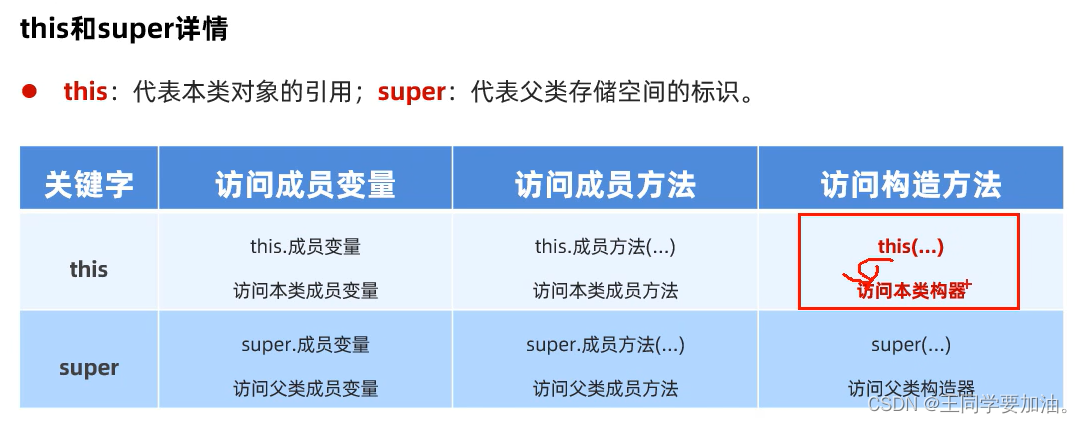
第十三节 继承
什么是继承? java中提供一个关键字extends,用这个关键字,我们可以让一个类和另一个类建立父子关系。 public class Student extends People{} student为子类(派生类),people为父类(基类或者超类…...

【优化】性能优化Springboot 项目配置内置Tomcat使用Http11AprProtocol(AIO)
Springboot 项目配置内置tomcat使用Http11AprProtocol(AIO) Windows版本 1.下载Springboot对应版本tomcat包 下载地址 Apache Tomcat - Apache Tomcat 9 Software Downloads 找到bin目录下 tcnative-1.dll 文件 2 放到jdk的bin目录下 Linux版本 在Springboot中内嵌的Tomcat默…...
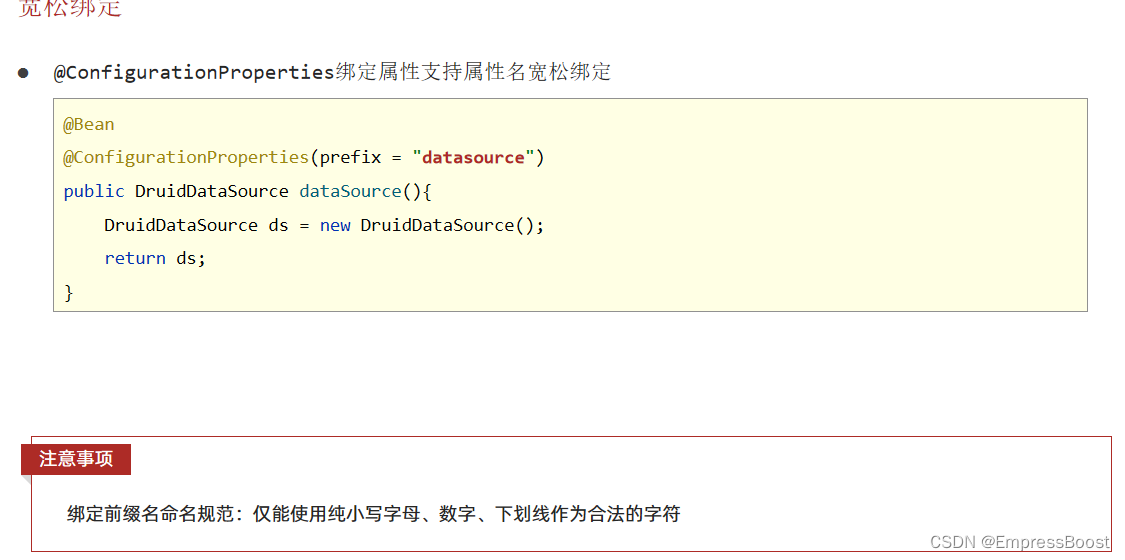
SpringBoot之@ConfigurationProperties、@EnableConfigurationProperties
ConfigurationProperties 这个注解不仅可以为yml某个类注入还可以为第三方bean绑定属性 为yml某个类注入 只要将对应的yml类对象声明实体pojo并交给spring容器管理,再在类上使用ConfigurationProperties绑定对应的类名即可 涉及到两个知识点,这个类对…...
数组一次性删除多条数据
需求描述 最后提交时删除表格中的空行 实现方法 单行删除 - 并不是一次性删除 表格每行的最后设置删除按钮,点击时将当前行的索引传递给方法,splice 删除当前行。 <el-table :data"tableData" class"myTable" border>..…...

相机删除照片如何恢复?一键解决它
相机删除照片如何恢复?喜欢用相机拍照的人,总会在空闲时多拍几张,这使我们相机中会储存大量的、各种各样的照片。等到回家后,在进行删除,并选出比较好的照片。但也很容易就误删了一些好看的照片。碰到这种意外事&#…...

vue3搭建教程(基于webpack+create-vue+ element-plus)
前言使用vue脚手架搭建vuetswebpack项目搭建步骤:下载node 版本可以 12 或者14或者 16.0,此次使用的>16.0版本,vue-cli通过npm i -g vue/cli 升级到了 vue cli v5.0.8建目录,如(vue3Study)用IDE工具打开…...

代码随想录算法训练营第四十二天 | leetcode 1049. 最后一块石头的重量 II,494. 目标和,474.一和零
代码随想录算法训练营第四十二天 | leetcode 1049. 最后一块石头的重量 II,494. 目标和,474.一和零1049. 最后一块石头的重量 II494. 目标和474.一和零1049. 最后一块石头的重量 II 题目: 有一堆石头,每块石头的重量都是正整数。…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...
