统计学 类别比变量的判断
文章目录
- 类别比变量的判断
- 一个类别变量的拟合优度检验
- 两个类别变量的独立性检验
- 两个类别变量的相关度检验
- 总结
类别比变量的判断
一个类别变量的拟合优度检验
只研究一个类别变量的时候,可以用 χ2\chi^2χ2 检验来判断各类别频数与某一期望频数是否一致。
- 观察频数:观察到的各类别实际的频数
- 期望频数:期望中各类别的频数
注意:这里频数不是比例
拟合优度检验:也称一致性检验,用于检验观察频数和期望频数是否一致,使用的统计量为 Pearson χ2\chi^2χ2 :
χ2=∑(fo−fe)2fe\chi^2=\sum\frac{(f_{o}-f_{e})^{2}}{f_{e}} χ2=∑fe(fo−fe)2
其中 χ2\chi^2χ2 服从自由度为 k−1k-1k−1 的 χ2\chi^2χ2 分布,kkk 为类别数目。
提出假设:
- H0H_{0}H0 :观察频数与期望频数无显著差异(无明显偏好)
- H1H_{1}H1 :观察频数与期望频数有显著差异(有明显偏好)
两类问题 : - 期望频数相等:每个类别的期望频数是相等的,比如我们要检验消费者对某些类别的产品是否有明显偏好
- 期望频数不等:每个类别的期望频数不等,比如我们要检验某个地区对某项政策的评价是否和全国人民对该政策的平均评价一致
计算完 χ2\chi^2χ2 后,也是用 PPP 值检验(取右尾概率)
两个类别变量的独立性检验
列联表与 χ2\chi^2χ2 独立性检验
列联表:两个或多个类别变量,每个类别变量包含许多类别,则将不同类别变量交叉分类的频数写成分布表,称为列联表
提出假设:(以下都是两个类别变量的情况)
- H0H_{0}H0 :两个变量独立(无关)
- H1H_{1}H1 :两个变量不独立(相关)
两个变量 χ2\chi^2χ2 独立性检验的统计量为:(自由度为 (r−1)(c−1)(r-1)(c-1)(r−1)(c−1))
χ2=∑∑(fo−fe)2fe\chi^2=\sum\sum\frac{(f_{o}-f_{e})^{2}}{f_{e}} χ2=∑∑fe(fo−fe)2
观察频数就是我们统计出来的值;单元格 ijijij 期望频数的计算方法为:
fe=RTin×CTjn×nf_{e}=\frac{RT_{i}}{n}\times\frac{CT_{j}}{n}\times n fe=nRTi×nCTj×n
其中:
- RTiRT_{i}RTi 为第 iii 行的频数之和,RTin\frac{RT_{i}}{n}nRTi 即为第 iii 行的类别所观察到的比例
- CTjCT_{j}CTj 为第 jjj 行的频数之和,CTjn\frac{CT_{j}}{n}nCTj 即为第 jjj 列的类别所观察到的比例
应用 χ2\chi^2χ2 检验应该注意的问题
应用 χ2\chi^2χ2 检验时,要求样本量足够大,特别是每个单元格的期望频数不能太小。否则期望频数在分母,太小的话会导致 χ2\chi^2χ2 变大,PPP 值变小,从而拒绝原假设。因此,应用 χ2\chi^2χ2 检验时对单元格的期望频数有以下要求:
- 如果仅有两个单元格,单元格的最小期望频数不应小于 5;
- 单元格两个以上时,期望频数小于 5 的单元格不能超过 20%;如果出现这种情况,可以通过合并类别的方式处理。
两个类别变量的相关度检验
如果前边独立性检验拒绝了 H0H_{0}H0 ,也就是说这两个变量不独立,此时可以进一步测度它们的关联程度,常使用 φ\varphiφ 系数、Cramer’s VVV 系数和列联系数作为检验统计量。
φ\varphiφ 系数
φ\varphiφ 系数主要用于 2×22\times22×2 列联表的相关性测量:
φ=χ2n\varphi=\sqrt{ \frac{\chi^2}{n} } φ=nχ2
对于 2×22\times22×2 列联表,φ\varphiφ 取值为 0∼10\sim 10∼1 ,越接近 1 表示两个变量的相关性越强;
当列联表变大时,φ\varphiφ 的值会随着变大,此时不好解释 φ\varphiφ 的含义。
Cramer’s VVV 系数
Cramer’s VVV 系数由 Cramer 提出,计算公式为:
V=χ2n×min((r−1),(c−1))V=\sqrt{ \frac{\chi^{2}}{n\times \min{((r-1),\,(c-1))}} } V=n×min((r−1),(c−1))χ2
其中 rrr 和 ccc 分别为行数和列数;当行数或列数为 222 时,Cramer’s VVV 系数就等于 φ\varphiφ 系数。
Cramer’s VVV 系数的取值总是在 0∼10\sim 10∼1 :
- 当两个变量独立时,V=0V=0V=0 ;
- 当两个变量完全相关时,V=1V=1V=1 ;
列联系数
列联系数主要用于大于 2×22\times22×2 的列联表,用 CCC 表示,计算公式为:
C=χ2χ2+nC=\sqrt{ \frac{\chi^{2}}{\chi^{2}+n} } C=χ2+nχ2
当两个变量独立时,C=0C=0C=0 ;但两个变量完全相关时,CCC 也不等于 111 ,因此对列联系数的解释就不够方便。
总结
相关文章:

统计学 类别比变量的判断
文章目录类别比变量的判断一个类别变量的拟合优度检验两个类别变量的独立性检验列联表与 χ2\chi^2χ2 独立性检验应用 χ2\chi^2χ2 检验应该注意的问题两个类别变量的相关度检验φ\varphiφ 系数Cramers VVV 系数列联系数总结类别比变量的判断 一个类别变量的拟合优度检验 …...

2.基于Label studio的训练数据标注指南:(智能文档)文档抽取任务、PDF、表格、图片抽取标注等
文档抽取任务Label Studio使用指南 1.基于Label studio的训练数据标注指南:信息抽取(实体关系抽取)、文本分类等 2.基于Label studio的训练数据标注指南:(智能文档)文档抽取任务、PDF、表格、图片抽取标注等…...

如何在openKylin操作系统上搭建Qt开发环境
一、获取linux系统下的Qt安装包 Qt官网下载地址:https://download.qt.io 国内镜像下载地址:https://mirrors.cloud.tencent.com/qt/ 。建议用镜像下载速度快。集成安装包在 official_releases/qt 目录下,新地址:https://downloa…...

T_SQL和SQL的区别
一. SQL Server和T-SQL的区别(⭐T-SQL 包含了 SQL)SQL Server是结构化查询语言,是目前关系型数据库管理系统中使用最广泛的查询语言T-SQL是标准SQL语言的扩展,是SQL Server的核心,在SQL的的基础上添加了变量,运算符,函数和流程控制等,Microso…...

用Python自己写一个分词器,python实现分词功能,隐马尔科夫模型预测问题之维特比算法(Viterbi Algorithm)的Python实现
☕️ 本文系列文章汇总: (1)HMM开篇:基本概念和几个要素 (2)HMM计算问题:前后向算法 代码实现 (3)HMM学习问题:Baum-Welch算法 代码实现(…...
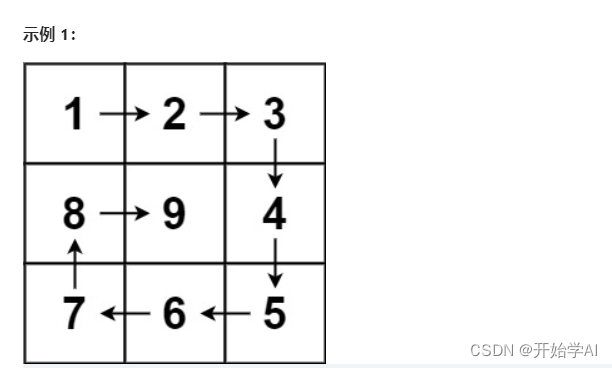
刷题笔记2 | 977.有序数组的平方 ,209.长度最小的子数组 ,59.螺旋矩阵II ,总结
977.有序数组的平方 给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。 输入:nums [-4,-1,0,3,10] 输出:[0,1,9,16,100] 解释:平方后,数组变为 […...
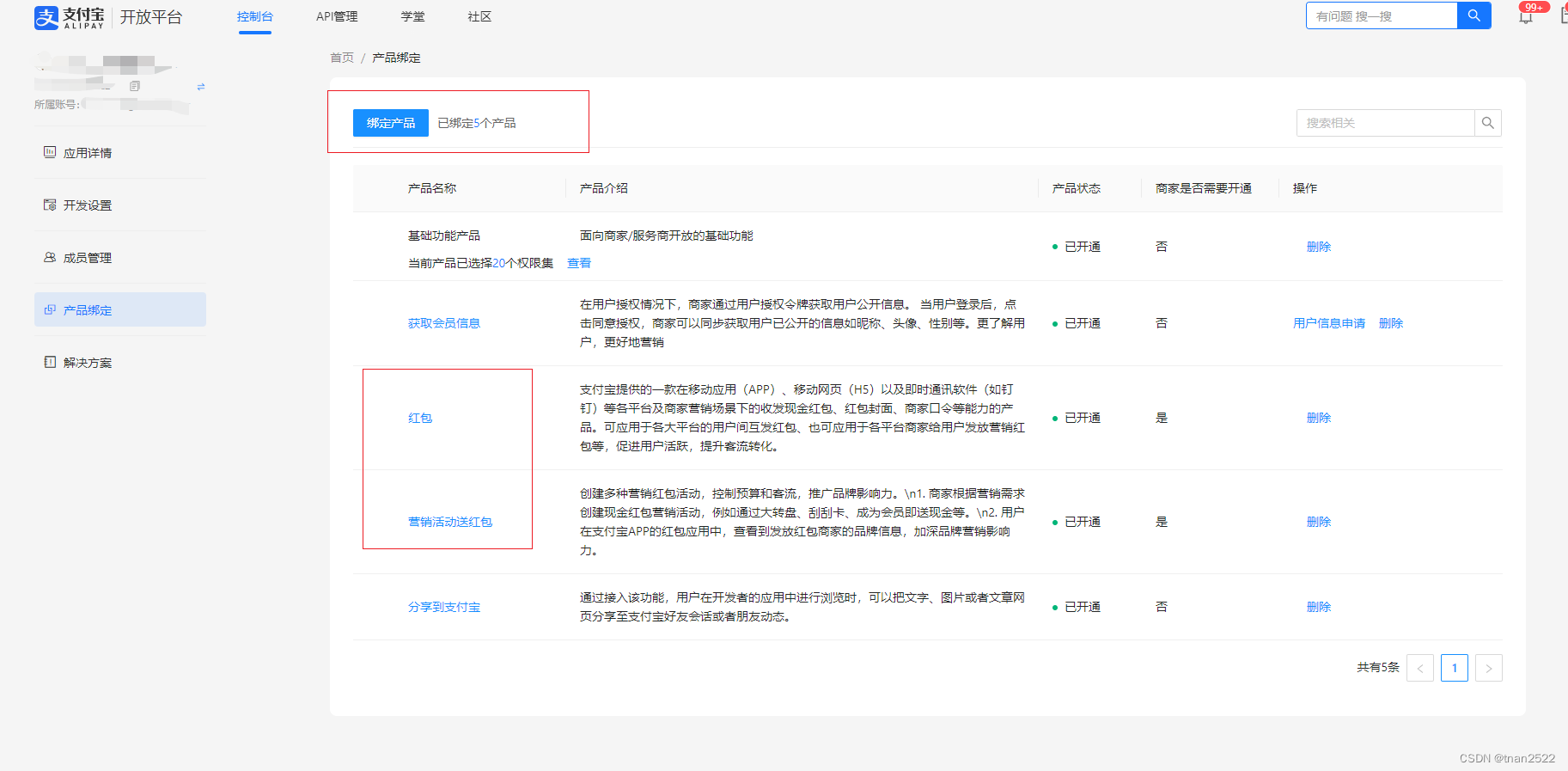
python 支付宝营销活动现金红包开发接入流程-含接口调用加签
1 创建网页/移动应用 2 配置接口加签方式 涉及到金额的需要上传证书,在上传页面有教程, 在支付宝开放平台秘钥工具中生成CSR证书,会自动保存应用公钥和私钥到电脑上,调用支付宝接口需要应用私钥进行加签 上传完CSR证书后会有三个…...

Python操作Windows
用python进行windows端UI自动化的库有很多,比如pywinauto等,本文介绍一个使用autoit3来实现的 pyautoit 库pyautoit 是一个用python写的基于AutoItX3.dll的接口库,用来进行windows窗口的一系列操作,也支持鼠标键盘的操作。安装pip…...
)
Aptos SDK交互笔记(一)
背景 之前我们已经了解TS的一些语法,接下来可以实战训练下,这系列的文章就会介绍如何通过Aptos官网提供的TypeScript SDK与Aptos进行交互,这篇文章主要讲的就是如何使用提供API在aptos区块链上转帐。 官网示例 官网提供了交互的例子&#…...
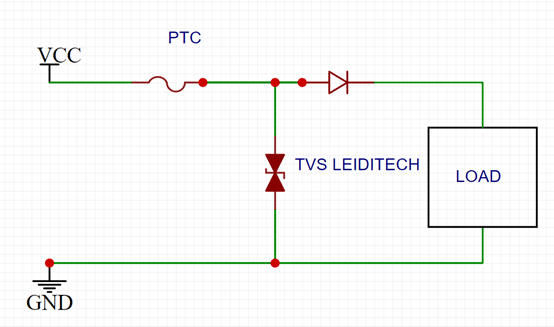
汽车 12V 和 24V 电池输入保护推荐
简介汽车电池电源线路在运行系统时容易出现瞬变。所需的典型保护包括过压、过载、反极性和跨接启动。在汽车 的生命周期中,交流发电机可能会被更换为非OEM 部件。售后市场上的交流发电机可能具有不同的负载突降(LOAD DUMP)保护或没有负载突降…...

龙蜥LoongArch架构研发全揭秘,龙芯开辟龙腾计划技术合作新范式
编者按:在开源新基建加快建设的背景下,越来越多的企业选择加入龙蜥社区,当前社区生态合作伙伴已突破 300 家。于是,龙蜥社区能为加入的企业提供哪些支持成为越多伙伴们更加关注的话题。本文将以龙蜥社区和龙芯中科联合研发龙蜥 Lo…...

剑指 Offer 16. 数值的整数次方
摘要 剑指 Offer 16. 数值的整数次方 本题的方法被称为快速幂算法,有递归和迭代两个版本。这篇题解会从递归版本的开始讲起,再逐步引出迭代的版本。当指数n为负数时,我们可以计算 x^(-n)再取倒数得到结果,因此我们只需要考虑n为…...
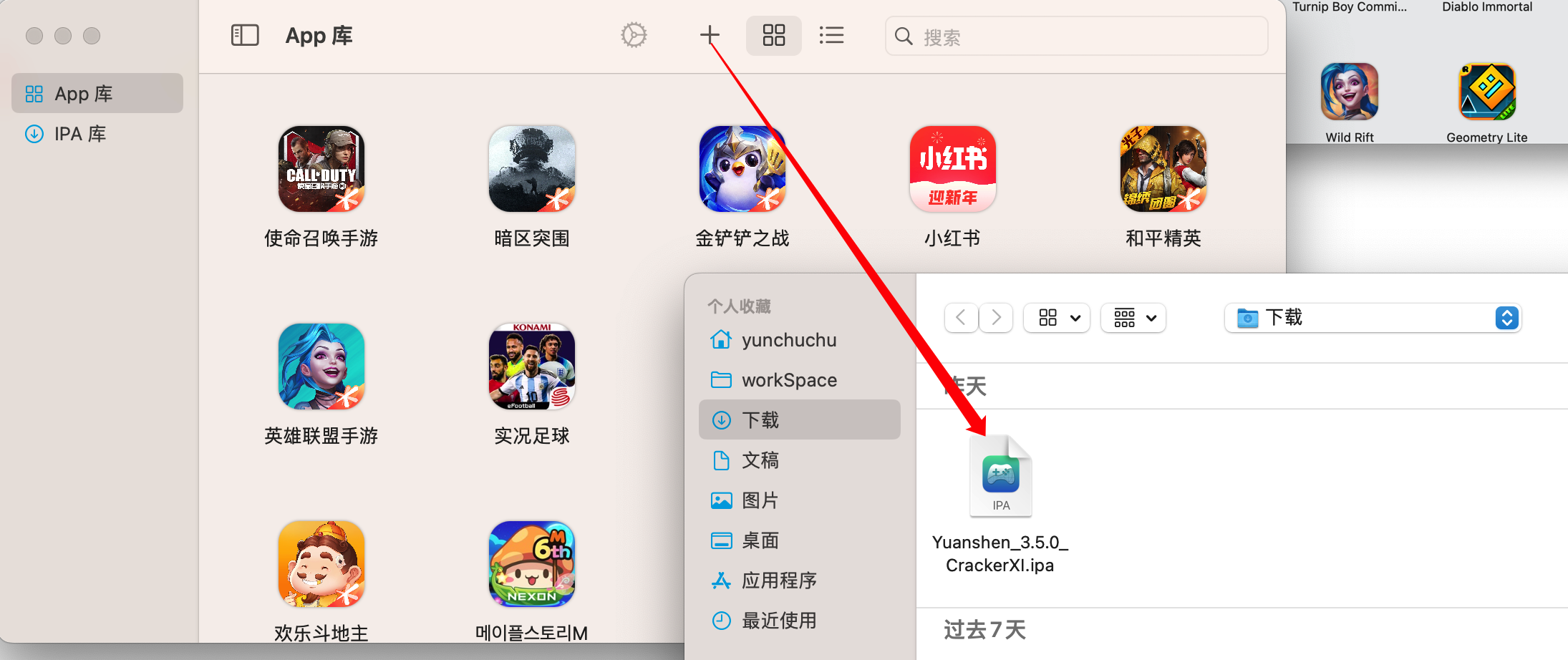
在苹果电脑 mac 上安装原神(playCover)
该方法只能在 M1、M2 mac 上安装原神 目录前言一、首先下载安装 playCover1. playCover 下载2. playCover 安装安装出现问题解决方法二、下载安装原神1.安装包下载2.安装原神三、登录、键盘映射及版本更新等问题登录键盘映射版本更新前言 最近买了新的mac,作者本人…...

数据结构考研习题精选
1 A假设比较t次,由于换或不换,则必然有2^t种可能。又设有n个关键字,n!排列组合,则必然有2^t&…...
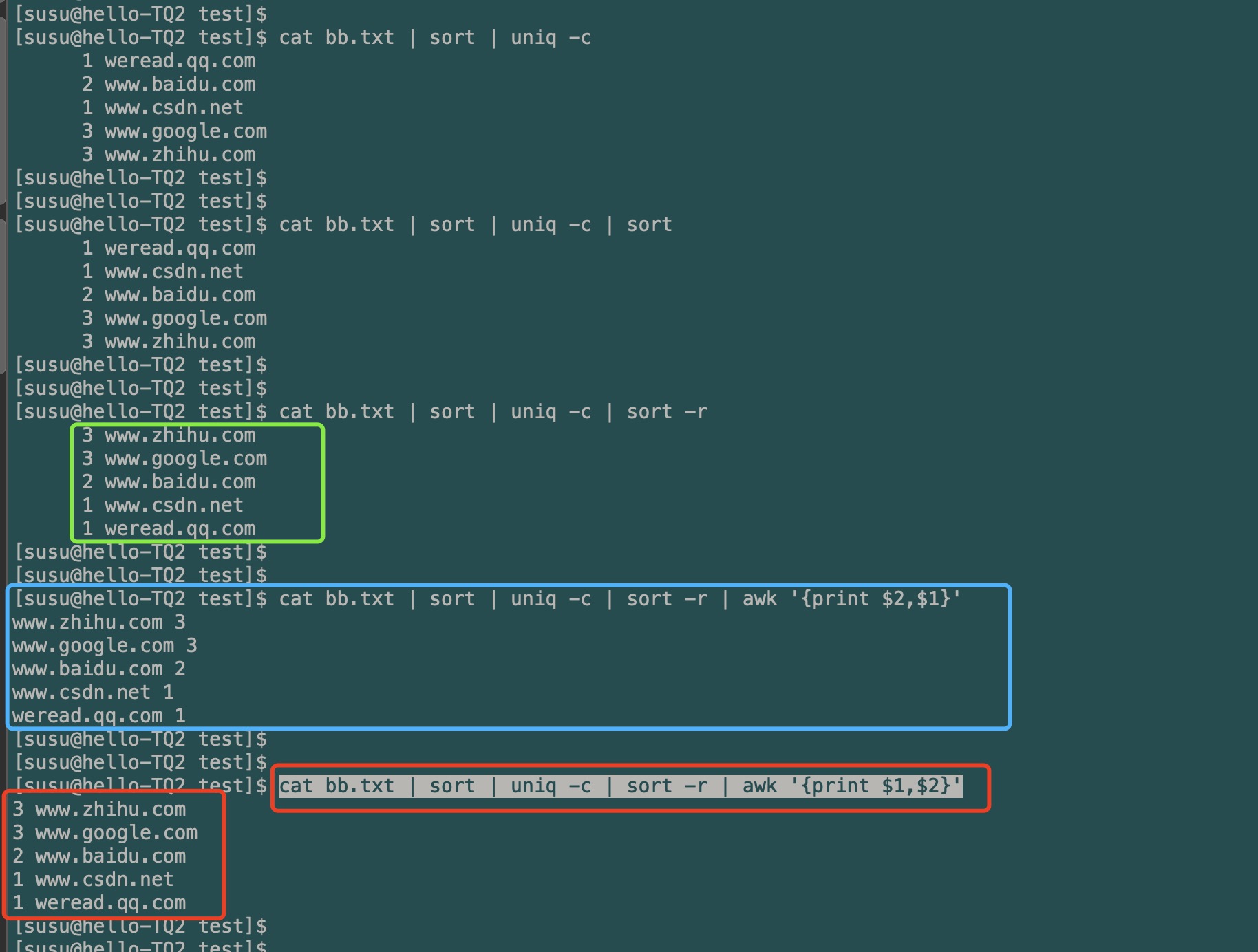
linux常用命令介绍 04 篇——uniq命令使用介绍(Linux重复数据的统计处理)
linux常用命令介绍 04 篇——uniq命令使用介绍(Linux重复数据的统计处理)1. uniq 使用语法2. sort 简单效果3. uniq 使用例子3.1 不加任何选项3.1.1 不用 sort 效果3.1.2 uniq 结合 sort 一起使用3.2 使用选项例子3.2.1 去重打印(或打印不重复…...
网站打不开数据库错误等常见问题解决方法
1、“主机开设成功!”上传数据后显示此内容,是因为西部数码默认放置的index.htm内容,需要核实wwwroot目录里面是否有自己的程序文件,可以删除index.htm。 2、恭喜,lanmp安装成功!这个页面是wdcp的默认页面&…...

爬虫实战进阶版【1】——某眼专业版实时票房接口破解
某眼专业版-实时票房接口破解 某眼票房接口:https://piaofang.maoyan.com/dashboard-ajax 前言 当我们想根据某眼的接口获取票房信息的时候,发现它的接口处的参数是加密的,如下图: 红色框框的参数都是动态变化的,且signKey明显是加密的一个参数。对于这种加密的参数,我们需要…...

大话数据结构-普里姆算法(Prim)和克鲁斯卡尔算法(Kruskal)
5 最小生成树 构造连通网的最小代价生成树称为最小生成树,即Minimum Cost Spanning Tree,最小生成树通常是基于无向网/有向网构造的。 找连通网的最小生成树,经典的有两种算法,普里姆算法和克鲁斯卡尔算法。 5.1 普里姆ÿ…...
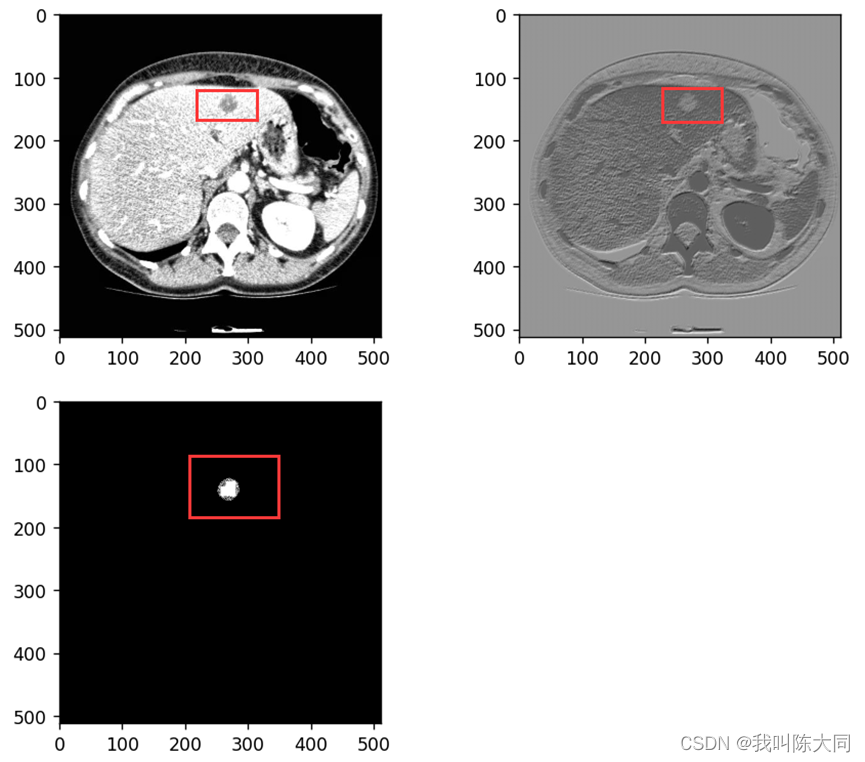
UNet-肝脏肿瘤图像语义分割
目录 一. 语义分割 二. 数据集 三. 数据增强 图像数据处理步骤 CT图像增强方法 :windowing方法 直方图均衡化 获取掩膜图像深度 在肿瘤CT图中提取肿瘤 保存肿瘤数据 四. 数据加载 数据批处理 编辑编辑 数据集加载 五. UNet神经网络模型搭建 单张图片…...

三周爆赚千万 电竞选手在无聊猿游戏赢麻了
如何用3个星期赚到1千万?普通人做梦都不敢想的事,电竞职业选手Mongraal却用几把游戏轻易完成,赚钱地点是蓝筹NFT项目Bored Ape Yacht Club(BAYC无聊猿)出品的新游戏Dookey Dash。 这款游戏类似《神庙逃亡》࿰…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...
