Opencv中的滤波器
一副图像通过滤波器得到另一张图像,其中滤波器又称为卷积核,滤波的过程称之为卷积。

这就是一个卷积的过程,通过一个卷积核得到另一张图片,明显发现新的到的图片边缘部分更加清晰了(锐化)。
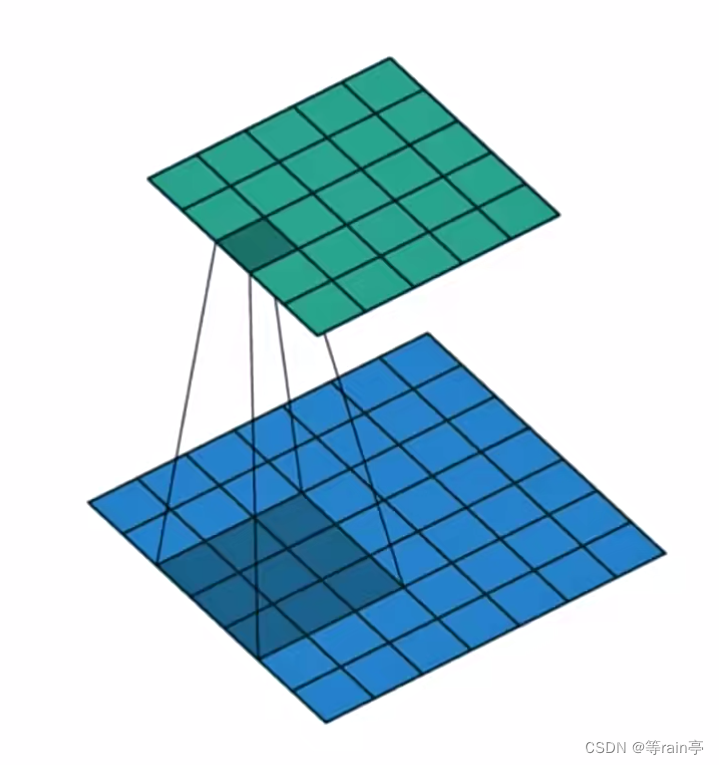
上图就是一个卷积的过程,下面的是原始图像,上面的是卷积核。卷积核以一定步长对于原始图像进行卷积处理,得到新的图像。
卷积核的大小:上图中的卷积核是5x5大小的卷积核。
锚点:就是卷积核最中心的位置
边界扩充:进行卷积后的图像一般比原始图像要小一点,为了和原始图像大小相同,就需要进行边界扩充。
步长:就是卷积核对原始图像进行扫描时,每一次移动几个像素。
卷积核的大小
(1)卷积核一般为奇数,如3x3,5x5,7x7;
一方面是为了增加padding的原因,就是进行扩充操作。
另一方面是保证锚点在中间(大家可以自己画一下3x3和4x4的矩阵进行思考有什么区别)防止位置发生偏移。
(2)卷积核大小的影响:卷积核越大,看到的信息(感受野)就越多,提取的特征就越好,同时计算量就越大。(目前很多深度学习领域中,使用两个或多个小的卷积核代替大的卷积核)
(3)边界扩充:当卷积核大于1且不进行边界扩充时,输出的尺寸一定会变小,所以需要进行边界扩充维持原来的大小。
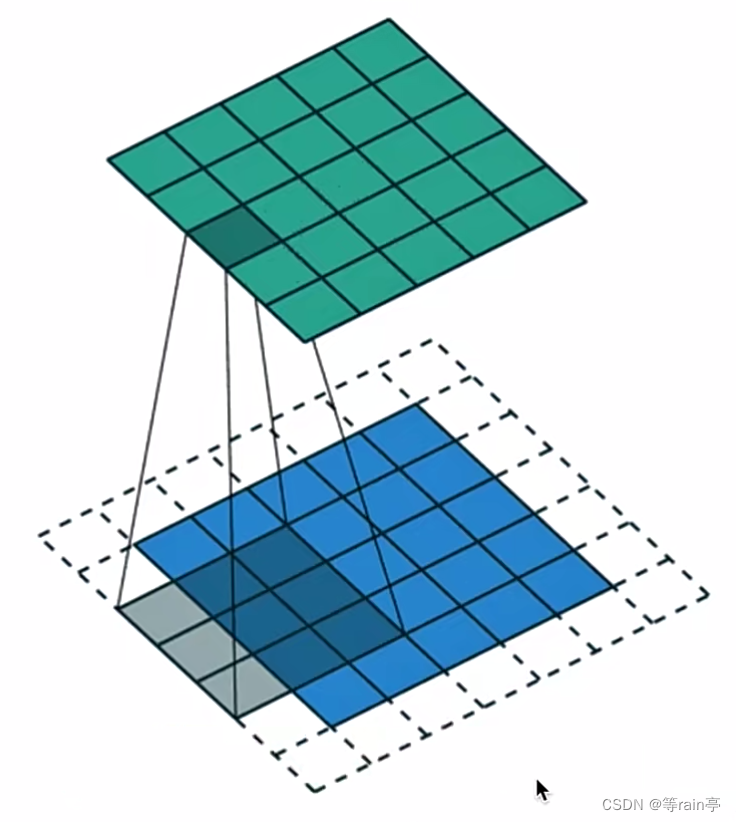
上图中下面的是原图,上面的是进行卷积后的图片,卷积核大小就是如图中的3x3,虚线部分就是进行边界扩充后的,所以很直观感受到,在进行边界扩充后才会变成原始的图像大小。

利用上述公式就可以得出不同的参数了,这对我们使用多大的卷积核,希望得到多大尺寸的图片都很有帮助。
(4)步长大小:
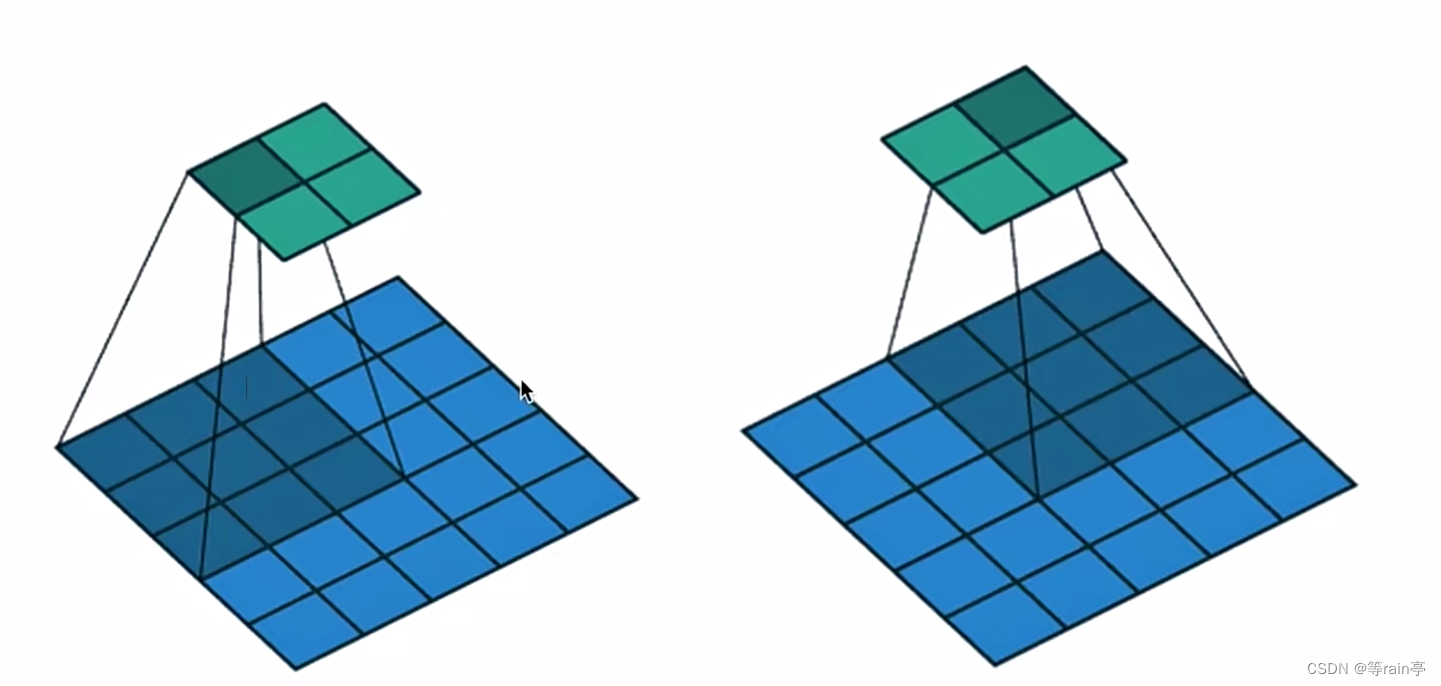
上图中的步长就是2。
低通滤波与高通滤波
低通滤波与高通滤波相关知识
低通滤波就是低于某个阈值是可以通过的
高通滤波就是高于某个阈值是可以通过的
低通滤波可以去除噪音或平滑图像(美颜中磨皮,去痘)
高通滤波可以帮助插值图像的边缘(抠图时需要边缘)
图像卷积
filter2D(src,ddepth,kernel,anchor,delta,borderType)
src:操作的原始图像
ddepth:位深,通常设置为-1
kernel:卷积核 (重要)
anchor:锚点(核的中心点)默认为-1,根据核直接去得到锚点
delta:原始图进行卷积后得到的图加上delta,默认为0
borderType:边界类型,加黑边等等 一般取默认值
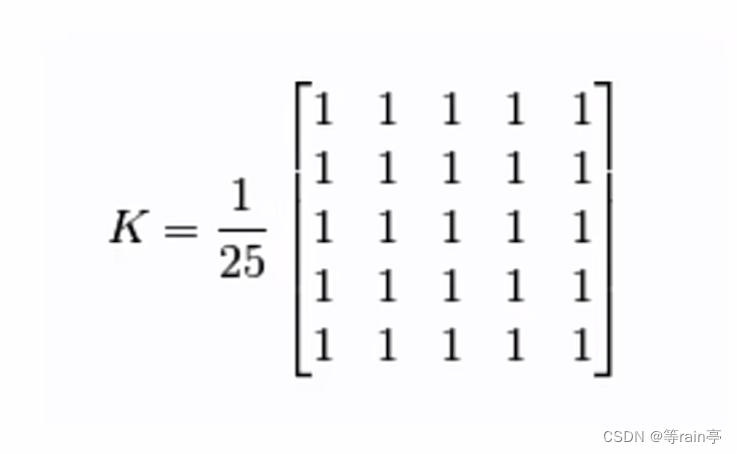
如图卷积核是上图,就意味着在原图中选5x5的像素每个值都乘1进行相加,得到的结果乘(1/25)就取得平均值,更加平滑。
图像卷积实战代码
import cv2
import numpy as npimg = cv2.imread('../MM/preview.jpg')# 自己设计的kernel的方法
kernel = np.ones((5, 5), np.float32) / 25
dst = cv2.filter2D(img, -1, kernel)cv2.imshow('dst', dst)
cv2.imshow('img', img)cv2.waitKey(0)

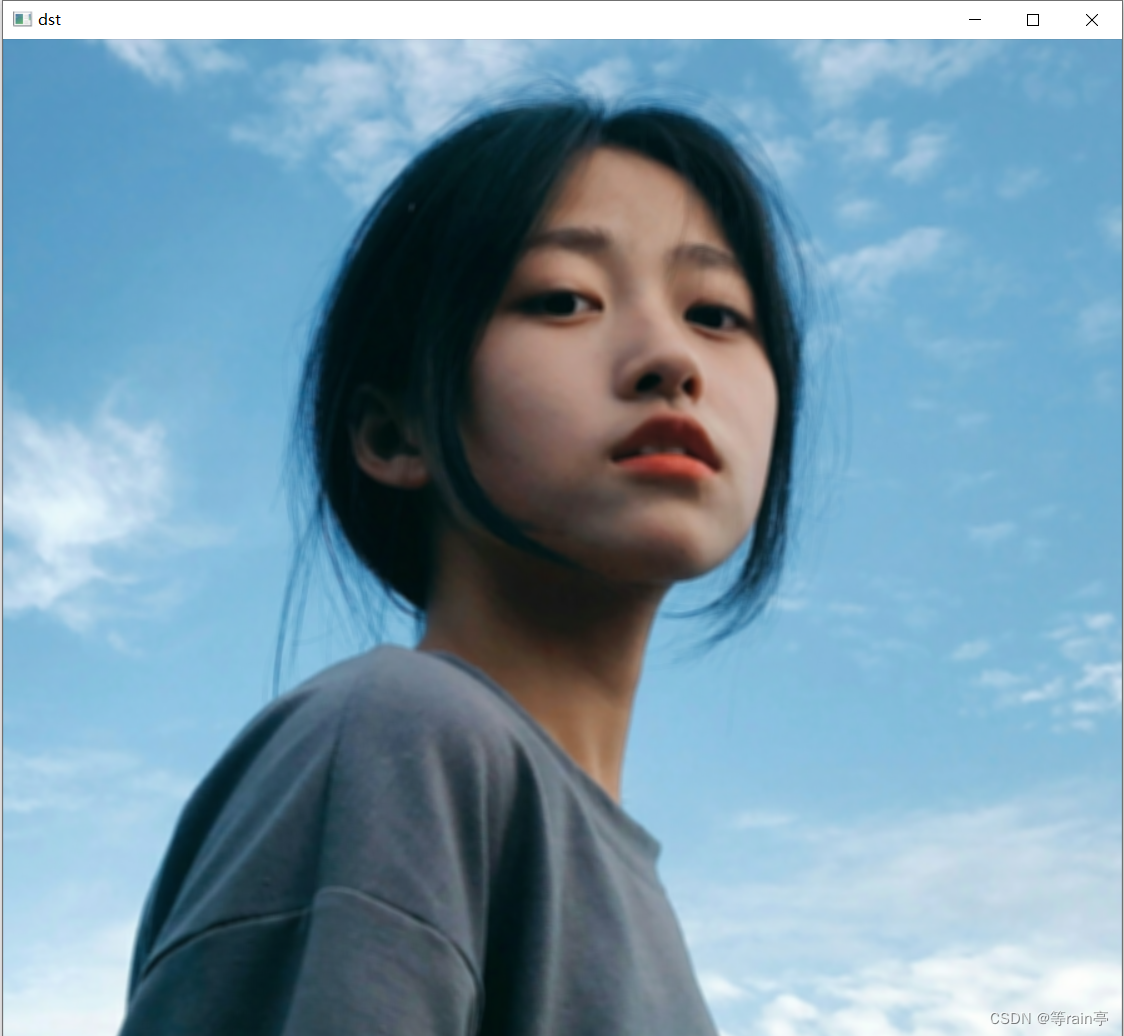
左边是原图,右边是处理后的图片。
看代码:我们设置的是5x5的全为1的矩阵,最后除25.得到结果更加平滑,但是清晰度明显下降了。(因此我们自己创的kernel往往不太合适,需要一些现存的效果较好的滤波器)
方盒滤波和均值滤波
方盒滤波:boxFilter(src,ddepth,ksize,anchor,normalize,borderType)
均值滤波:blur(src,ksize,anchor,borderType)
src:处理的图像
ddepth:位深,通常设置为-1
ksize:kernel size 卷积核大小
anchor:锚点(核的中心点)默认为-1,根据核直接去得到锚点
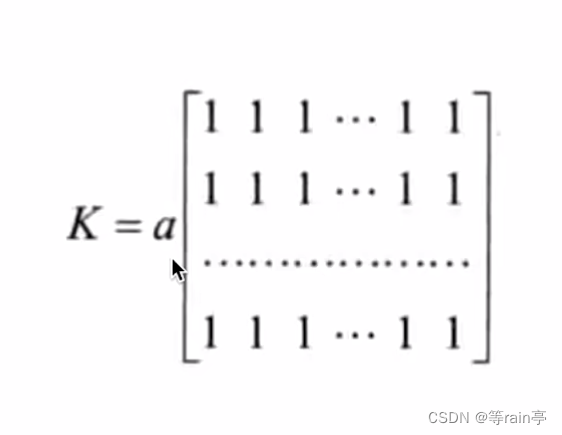
normalize:当normalize为True时,a=1/(W*H) 此时会退化成均值滤波
当normalize为False时,a=1 下图就是方盒滤波的卷积核
borderType:边界类型,加黑边等等 一般取默认值 。
方盒滤波和均值滤波实战代码
均值滤波:
# 均值滤波
dst = cv2.blur(img, (5, 5)) # 这个是均值滤波 用blur 其结果和自己设计kernel的结果相同结果和我们在第二部分自己设置kernel的结果相同,因为此时矩阵进行相乘后也是除25。
方盒滤波:
# 这种是方盒滤波,其初始中normalize为true变成均值滤波,如果想变成方盒滤波需要把normalize设置false
dst = cv2.boxFilter(img, -1, (5, 5), False)
dst1 = cv2.boxFilter(img, -1, (5, 5), True)
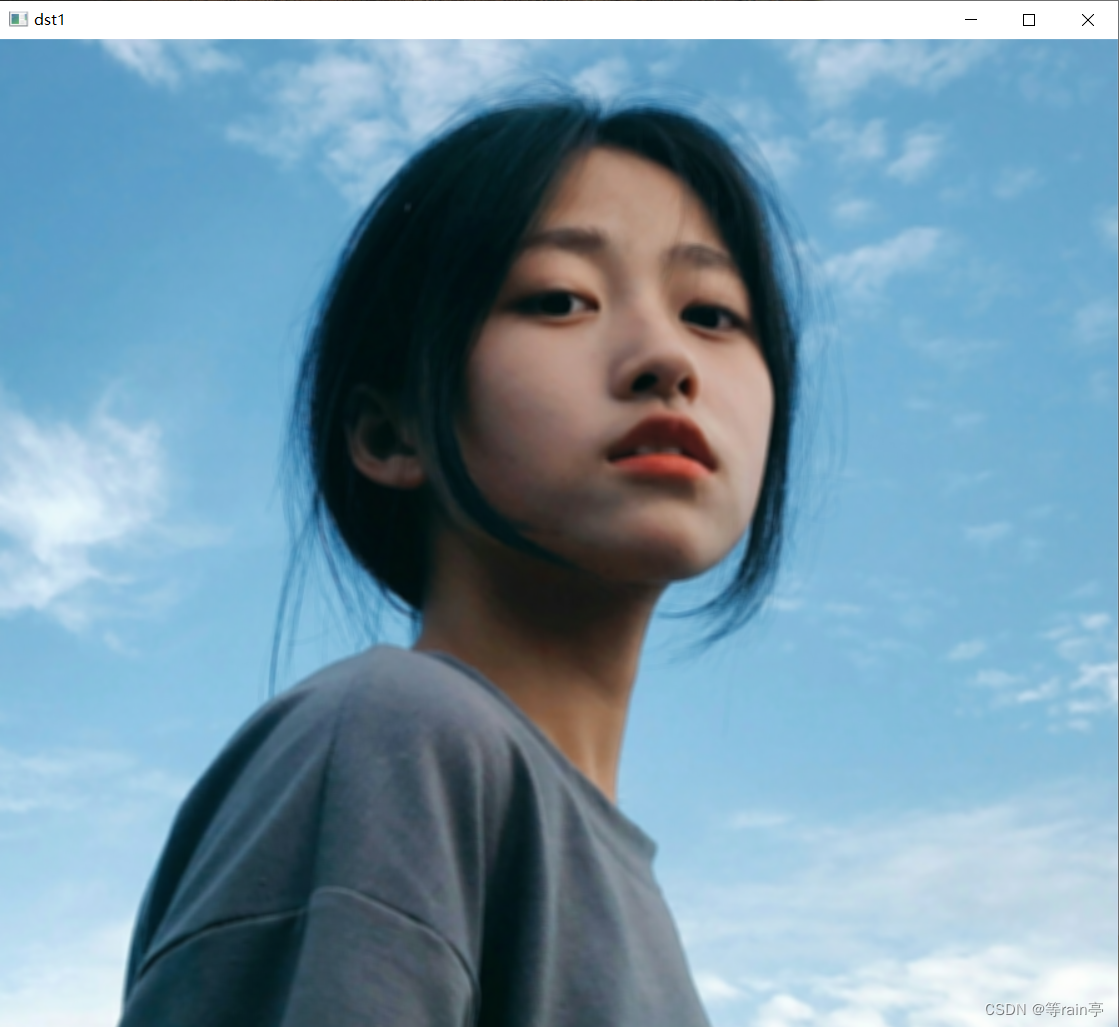
左边的是通过方盒滤波得到的结果,右边是均值滤波得到的结果。
高斯滤波
高斯滤波相关知识
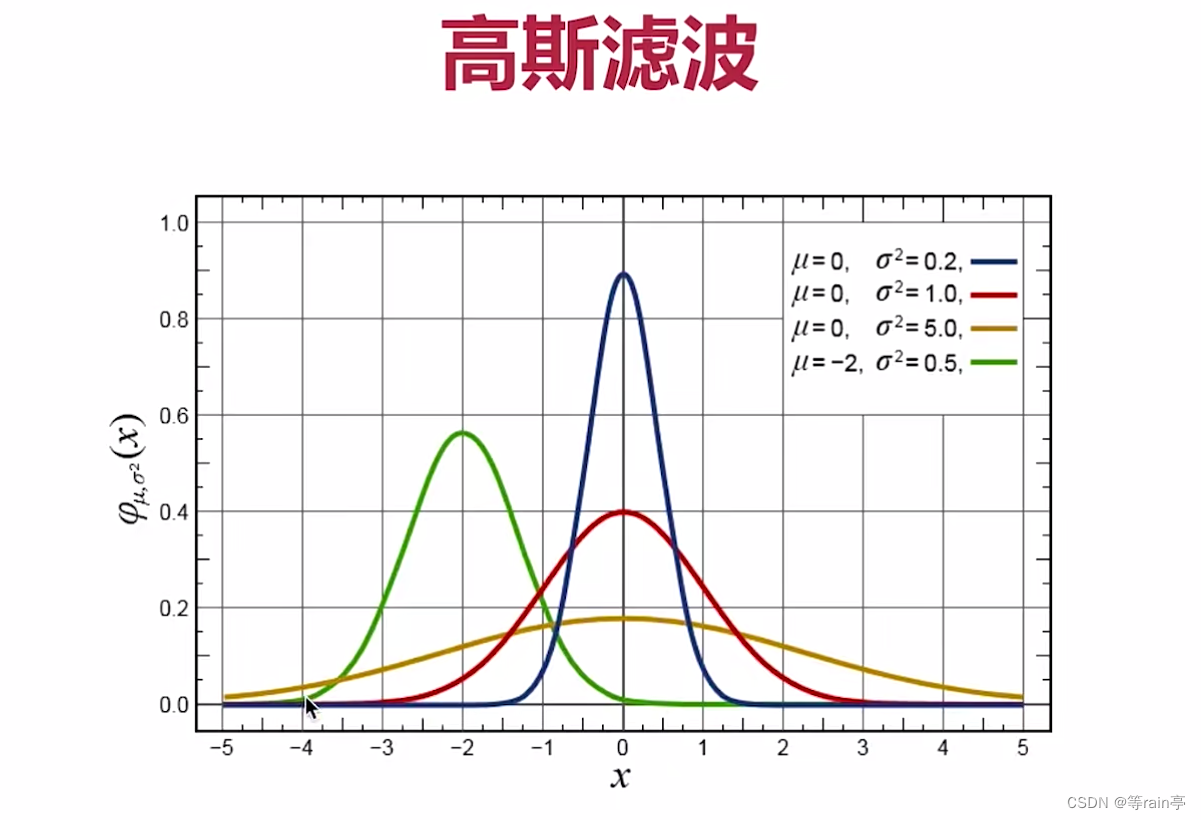
上图就是高斯滤波,发现一条曲线越靠近中间值越大(权重越大)
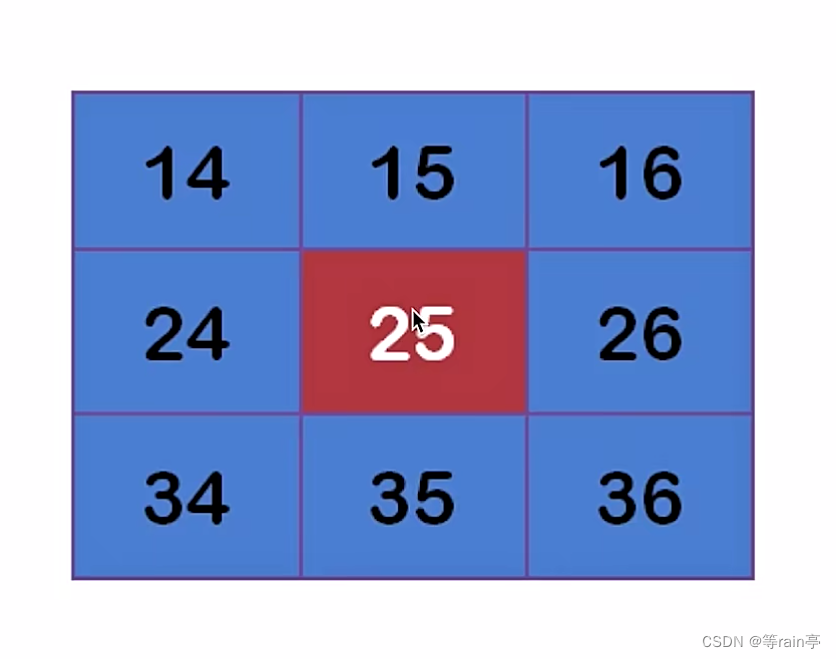
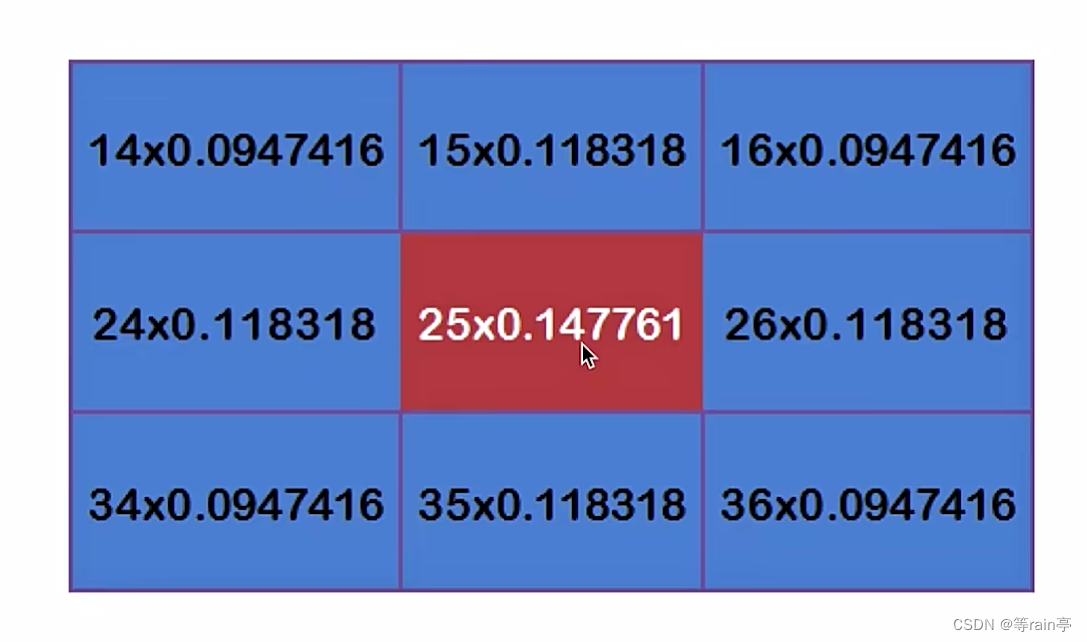
左边这张图代表的是矩阵中每个位置的大小,最中心的大小不一定是最大的(虽然第一张图25相较于周围较大), 但是最中心点的权重一定是最大的,并且越靠近中心权重越大(如第二张图,每一个数值乘一个权重的数值)
高斯滤波API:GaussianBlur(img,kernel,sigmaX,sigmaY,……)
img:需要对哪个图像进行处理
kernel:卷积核(大小) kernelsize
sigmaX,sigmaY:到中心点的延展宽度
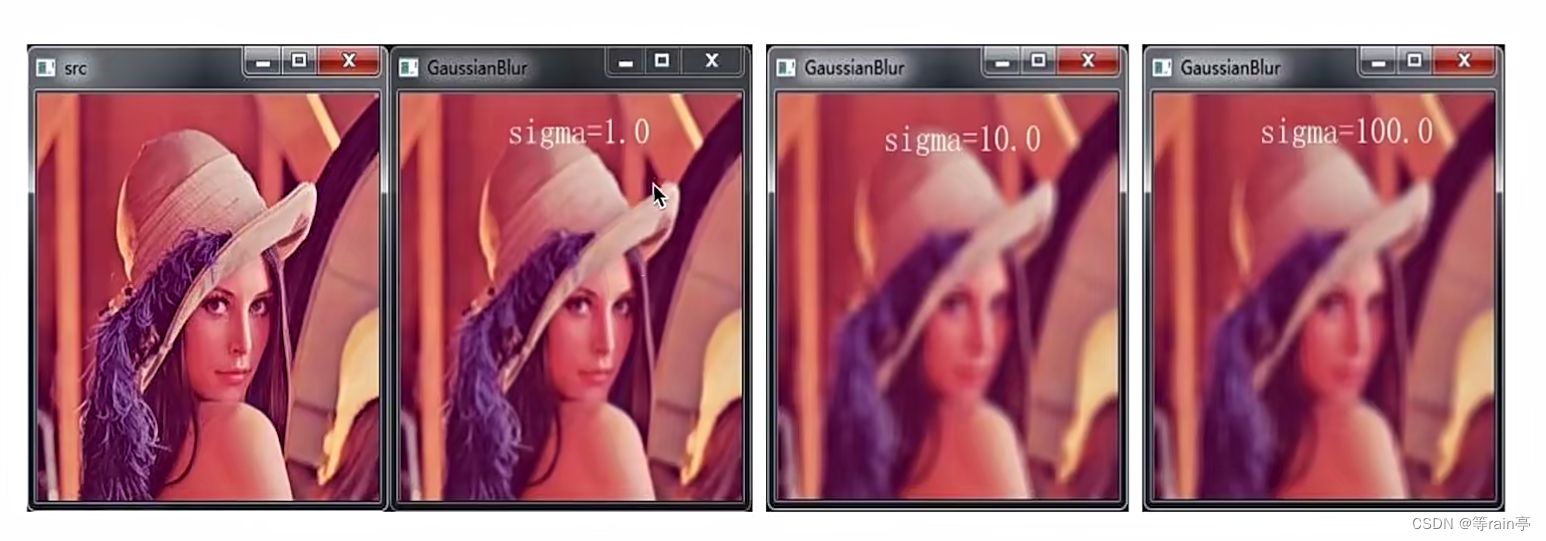
可以看出不同的sigma值的结果,如果没有sigma时,就看kernelsize,如下图。

高斯滤波实战代码
# 高斯滤波(解决高斯滤波,测量值会在均值附近产生大量的值,而离均值较远的值则会较少出现。)
# 设计中的锚点附近的权值较大
dst = cv2.GaussianBlur(img1, (5, 5), sigmaX=1)

左边是原图,发现每个环里面有很多的噪声点,经过高斯滤波后发现很多的噪声点都被去掉了,但是边缘部分也被处理掉了。(大家也可以自己去尝试改变sigma的值,看看会出现什么样的结果)
高斯滤波主要就是解决高斯噪点。
中值滤波
中值滤波相关知识
假如现在有一个数组[1556789],中值滤波就是取其中的中间值作为卷积后的结果值。
所以,当使用卷积核去卷积时,每一次都会对卷积后的结果进行排序,最后选择中间值。
中值滤波主要针对胡椒噪声(整张图像都有噪声)有很好的效果。
中值滤波API:medianBlur(img,ksize)
img:就是对哪张图片进行操作
ksize:kernelsize 卷积核的大小
中值滤波实战代码
# 中值滤波(解决胡椒噪音)
dst = cv2.medianBlur(img2, 7) 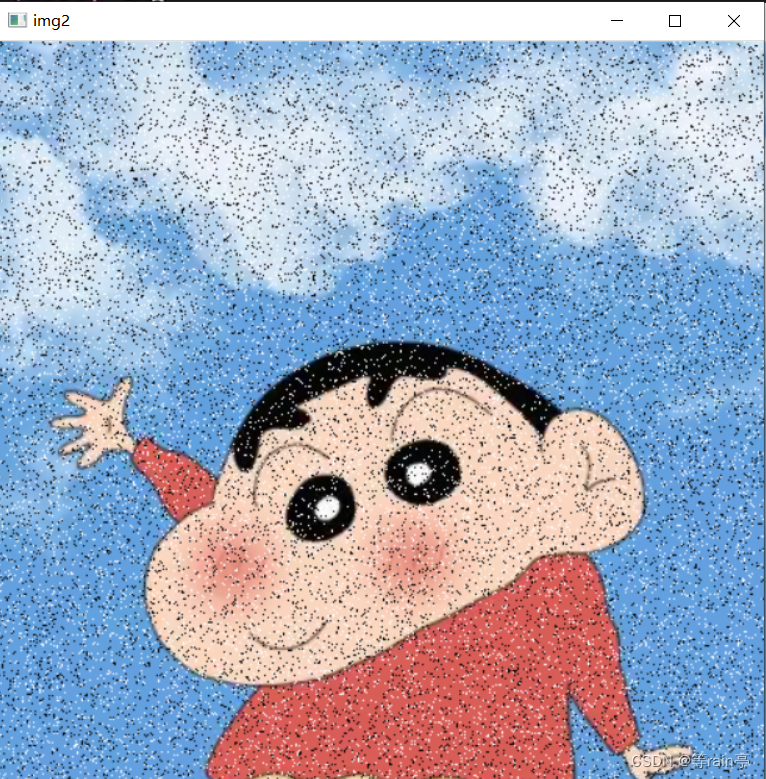
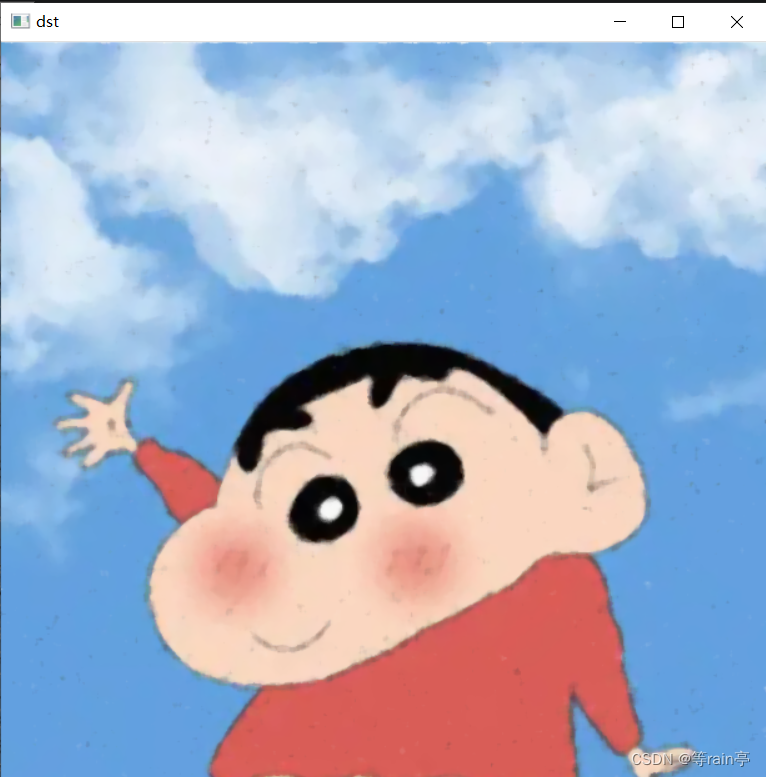
左边是具有胡椒噪声的原图,右边是处理后的图片。 但是边缘也是被弱化了。
双边滤波
双边滤波相关知识
可以保留边缘,同时对边缘内的区域进行平滑处理。(大家思考,当时我们使用高斯滤波去除区域内的高斯噪声,但是边缘被弱化了。那是否我们可以使用双边滤波解决边缘弱化的问题?)
双边滤波应用于美颜。

对于输入图像来看,边沿就是色差特别大的区域,双边滤波并没有对其进行处理,而是将边沿两边进行平滑处理。
双边滤波API:bilateralFilter(img,d,sigmaColor,sigmaSpace,……)
img:就是对哪张图片进行操作
d:直径(可以认为就是核的大小)
sigmaColor:对边沿的控制,在一定范围就不处理边沿
sigmaSpace:对边沿两边的控制,在一定范围内进行平滑处理
双边滤波实战代码
# 双边滤波(可以保留边缘,同时对边缘内的区域进行平滑处理)(主要作用是进行美颜)
dst = cv2.bilateralFilter(rita, 7, 20, 50)
# dst1=cv2.bilateralFilter(rita,20,20,50) #相比d=7,d=10磨皮效果更好

左边是原图,右边是进行双边滤波处理后的图片。大家也可以尝试去修改d等参数获得一个更好的美颜效果。
—————————————以下都是高通滤波——————————————————————
高通滤波
检测边缘
常见的高通滤波:
Sobel(索贝尔)(首先使用了高斯滤波去噪,后又一阶导,得到边沿)
Scharr(沙尔)当Sober的卷积核大小设置为-1就变成了Scharr
Sobel(索贝尔)和Scharr(沙尔)都只能对一个方向进行处理,所以得到结果后需要把x,y得到的结果加到一起
Laplacian(拉普拉斯)可以直接求出x,y方向的边缘。对于噪音比较敏感,因为内部没有降噪的处理。
大家可能这样看x,y方向的边缘不太理解,等后面实战会有所展示。
Sobel算子
Sobel算子相关知识点
先向x方向上求导,然后在y方向求导。最终结果相加。
Sobel算子API:Sobel(src,ddepth,dx,dy,ksize=3,scale=1,delta=0,borderType=BORDER_DEFAULT)
src:对哪张图进行操作
ddepth:输出图像的位深
dx=1 就检测出y边缘 dy=1就检测出x边缘
ksize:kernelsize 卷积核大小 。卷积核大小设置为-1就变成了Scharr
scale:用于缩放
delta:对结果进行加delta
borderType:边缘类型
Sobel实战代码
import cv2
import numpy as npimg = cv2.imread('../MM/chess.png')# 索贝尔算子
# y方向的边缘
y = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=5) # 3x3的卷积核就变成了scharr# x方向的边缘
x = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=5) # 默认ksize为3dst = x + y # python自身带的
dst1 = cv2.add(x, y)cv2.imshow('img', img)
cv2.imshow('y', y)
cv2.imshow('x', x)
cv2.imshow('dst', dst)cv2.waitKey(0)


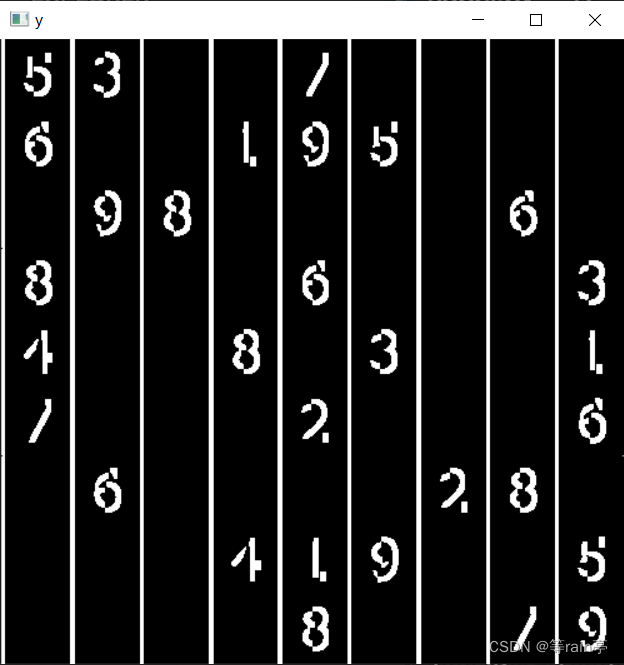

第一张图是原图,第二张代码中使dy=1,得到x方向上的边沿。第三张代码中使dx=1,得到y方向上的边沿。最后代码中的dst和dst1得到的效果都是一样的,将x,y方向上的边沿加在一起。
Sobel不可以将dx,dy都设置成1。大家可以自己设置一些看看会出现什么样的结果。
Scharr算子
Scharr算子相关知识点
与Sobel类似,但是使用的kernel值不同。Scharr只支持3x3的卷积核。
Scharr只能求x方向或y方向的边缘。
Scharr的API :Scharr(src,ddepth,dx,dy,scale=1,delta=0,borderType=BORDER_DEFAULT)
src:对哪张图进行操作
ddepth:输出图像的位深
dx=1 就检测出y边缘 dy=1就检测出x边缘
scale:用于缩放
delta:对结果进行加delta
borderType:边缘类型
Scharr算子实战代码



得到的图像和Sobel的图像相同。 但是Scharr还识别出来一些细小的点。(Soble用的较多)
拉普拉斯算子
拉普拉斯算子相关知识
可以同时求两个方向的边缘,不用和Sobel或Scharr一样单独求x,y。
拉普拉斯算子对于噪声比较敏感,所以一般需要进行去噪后再使用拉普拉斯。
拉普拉斯API:Laplacian(src,ddepth,ksize=1,scale=1,borderType=BORDER_DEFAULT)
src:对哪张图进行操作
ddepth:输出图像的位深
ksize=kernelsize卷积核大小
scale:用于缩放
borderType:边缘类型
拉普拉斯实战代码
ldst = cv2.Laplacian(img, cv2.CV_64F, ksize=5)


左图是原图,右图是进过拉普拉斯处理后的图片。由于原图中噪音比较少,所以直接使用了拉普拉斯。
边缘检测Canny(重要)
Canny的相关知识
对于Sobel,Scharr需要分别对x,y进行操作,拉普拉斯需要进行降噪处理。
而Canny相较于这三种就比较完美,效果好,并且简单。
canny使用的是5x5的高斯滤波消除噪声(比拉普拉斯好),计算图像梯度方向(0,45,90,135)(比Soble,Scharr全面),取局部最大值,阈值计算。
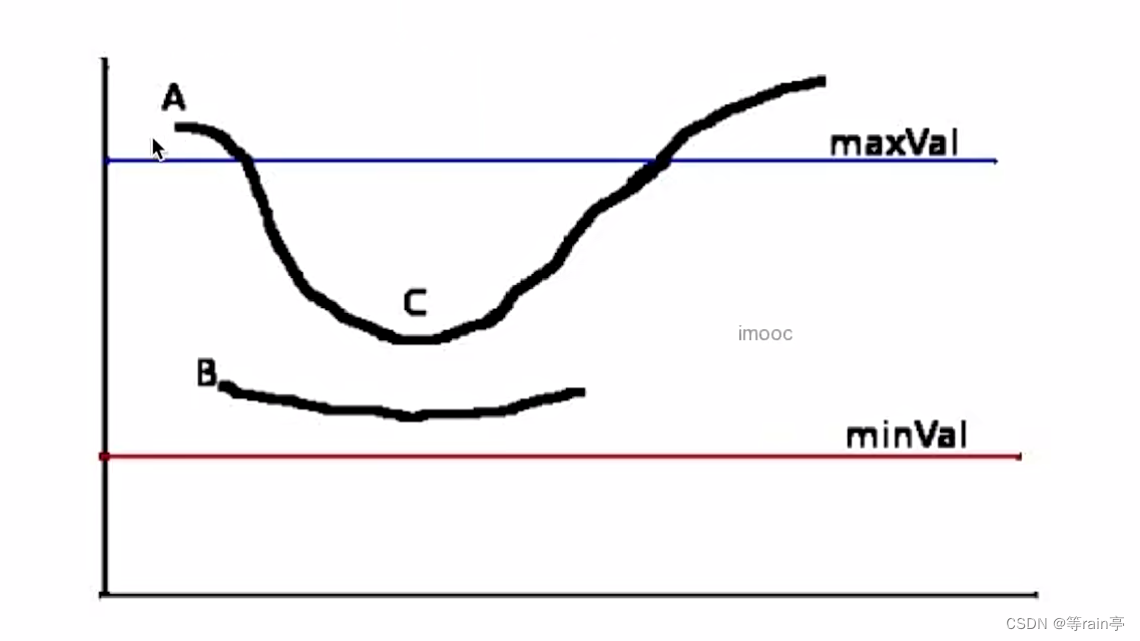
阈值计算原理,超过maxval的一定是边缘,小于minval的一定不是边缘。再maxval和minval之间的可能是可能不是,如果像c点一样于超过maxval确定是边缘的线是连续的,那c点就是边缘,否则像b一样就不是边缘。
Canny的API:Canny(img,minval,maxval,……)
img:对哪张图片进行操作
minval,maxval:要进行手动设置阈值
Canny实战代码
import cv2
import numpy as npimg = cv2.imread('../MM/preview.jpg')dst = cv2.Canny(img, 180, 200)cv2.imshow('img', img)
cv2.imshow('dst', dst)cv2.waitKey(0)
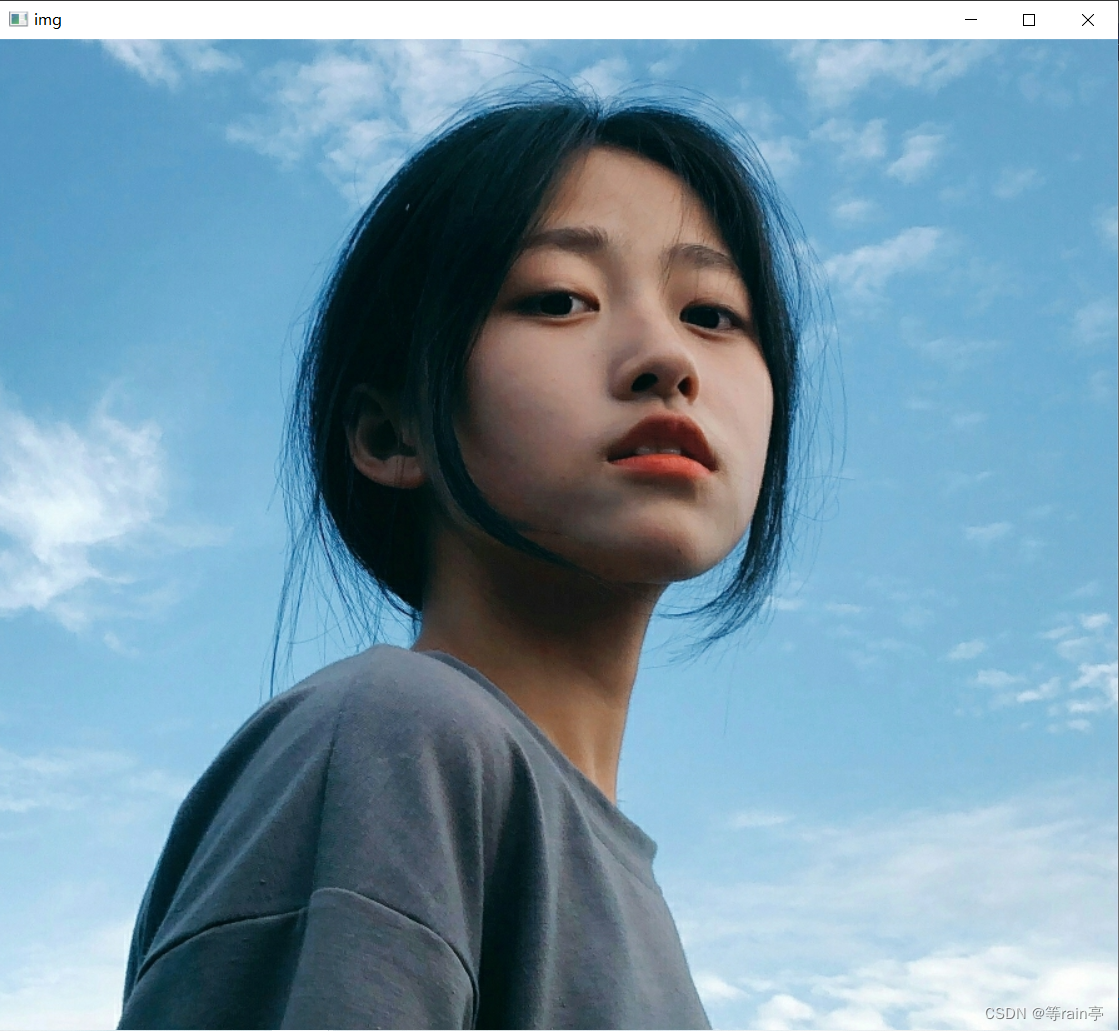
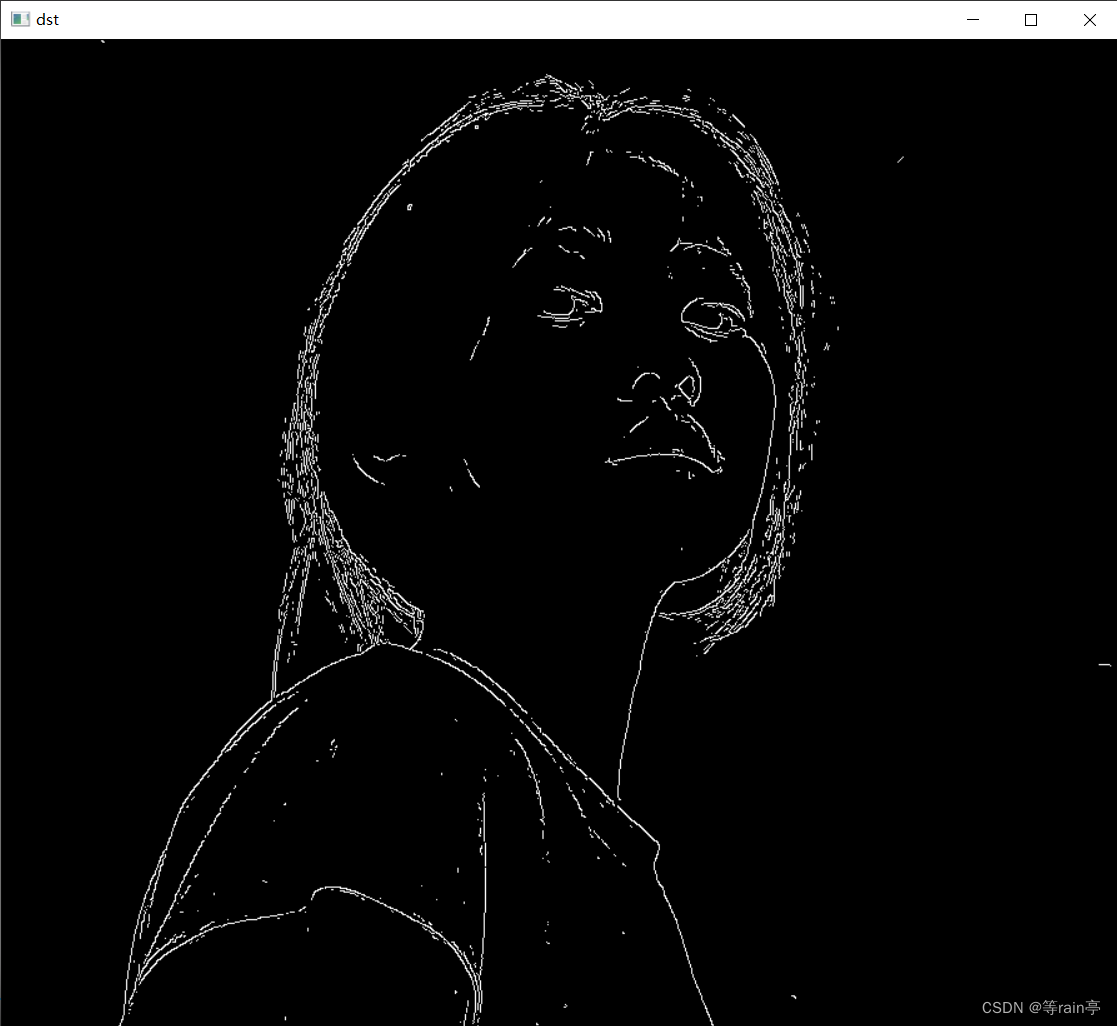
大家可以根据自己的图片改变相关的maxval和minval来体会不同的感觉。
相关文章:

Opencv中的滤波器
一副图像通过滤波器得到另一张图像,其中滤波器又称为卷积核,滤波的过程称之为卷积。 这就是一个卷积的过程,通过一个卷积核得到另一张图片,明显发现新的到的图片边缘部分更加清晰了(锐化)。 上图就是一个卷…...

<JavaEE> 基于 TCP 的 Socket 通信模型
目录 一、认识相关API 1)ServerSocket 2)Socket 二、TCP字节流套接字通信模型概述 三、回显客户端-服务器 1)服务器代码 2)客户端代码 一、认识相关API 1)ServerSocket ServerSocket 常用构造方法ServerSocke…...
[THUPC 2024 初赛] 二进制 (树状数组单点删除+单点查询)(双堆模拟set)
题解 题目本身不难想 首先注意到所有查询的序列长度都是小于logn级别的 我们可以枚举序列长度len,然后用类似滑动窗口的方法,一次性预处理出每种字串的所有出现位置,也就是开N个set去维护所有的位置。预处理会进行O(logn)轮,每…...
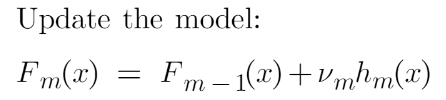
机器学习算法(11)——集成技术(Boosting——梯度提升)
一、说明 在在这篇文章中,我们学习了另一种称为梯度增强的集成技术。这是我在机器学习算法集成技术文章系列中与bagging一起介绍的一种增强技术。我还讨论了随机森林和 AdaBoost 算法。但在这里我们讨论的是梯度提升,在我们深入研究梯度提升之前…...

使用GBASE南大通用负载均衡连接池
若要使用负载均衡连接池功能,需要在连接串中配置相关的关键字。有关更详细的关键字信息在 GBASE南大通用 连接参数表‛中介绍。假设存在如下场景: 现有集群中存在 4 个节点: 192.168.9.173, 192.168.9.174, 192.168.9.175, 192.168.9.17…...
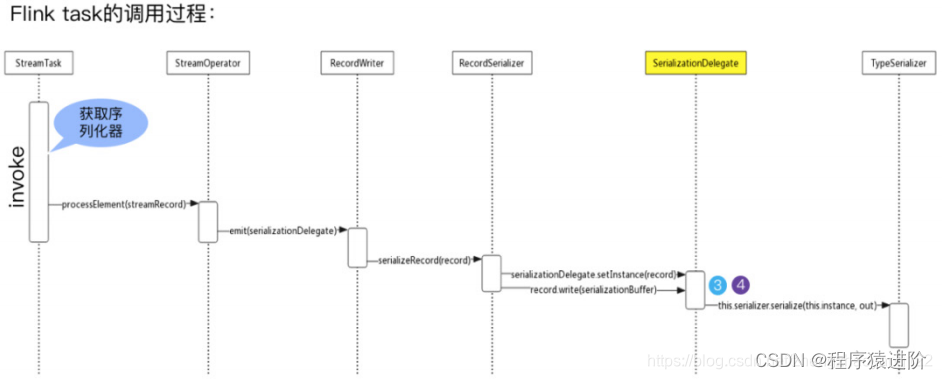
Flink 数据序列化
为 Flink 量身定制的序列化框架 大家都知道现在大数据生态非常火,大多数技术组件都是运行在JVM上的,Flink也是运行在JVM上,基于JVM的数据分析引擎都需要将大量的数据存储在内存中,这就不得不面临JVM的一些问题,比如Ja…...
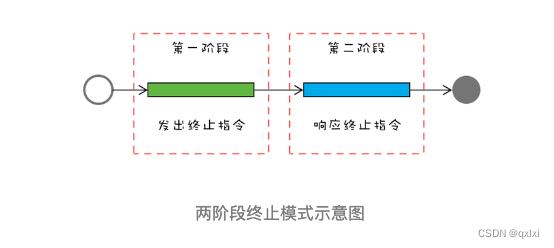
【并发设计模式】聊聊两阶段终止模式如何优雅终止线程
在软件设计中,抽象出了23种设计模式,用以解决对象的创建、组合、使用三种场景。在并发编程中,针对线程的操作,也抽象出对应的并发设计模式。 两阶段终止模式- 优雅停止线程避免共享的设计模式- 只读、Copy-on-write、Thread-Spec…...
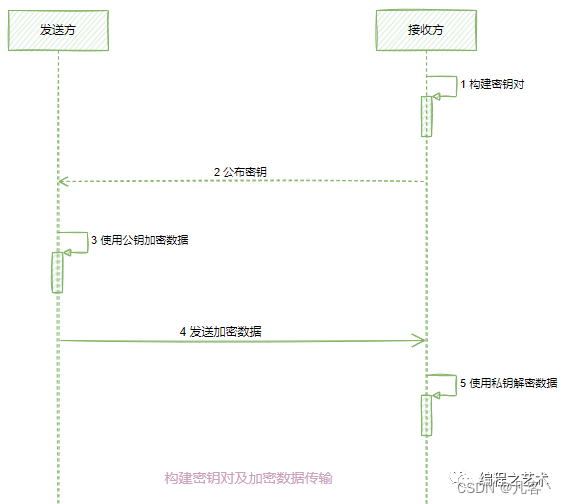
Java实现非对称加密【详解】
Java实现非对称加密 1. 简介2. 非对称加密算法--DH(密钥交换)3. 非对称加密算法--RSA非对称加密算法--EIGamal5. 总结6 案例6.1 案例16.2 案例2 1. 简介 公开密钥密码学(英语:Public-key cryptography)也称非对称式密…...

simulinkveristandlabview联合仿真——模型导入搭建人机界面
目录 1.软件版本 2.搭建simulink仿真模型 编译错误 3.导入veristand并建立工程 4.veristand导入labview labview显示veristand工程数据 labview设置veristand工程数据 运行labview工程 1.软件版本 matlab2020a,veristand2020 R4,labview2020 SP…...
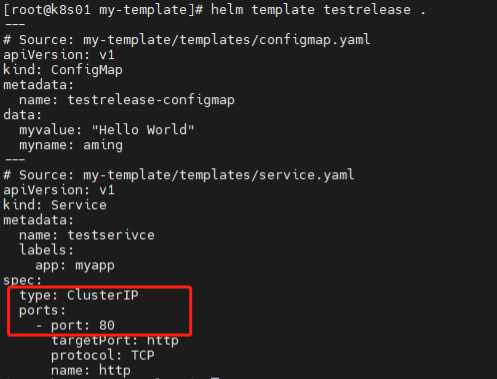
k8s中Helm工具实践
k8s中Helm工具实践 1)安装redis-cluster 先搭建一个NFS的SC(只需要SC,不需要pvc),具体步骤此文档不再提供,请参考前面相关章节。 下载redis-cluster的chart包 helm pull bitnami/redis-cluster --untar…...
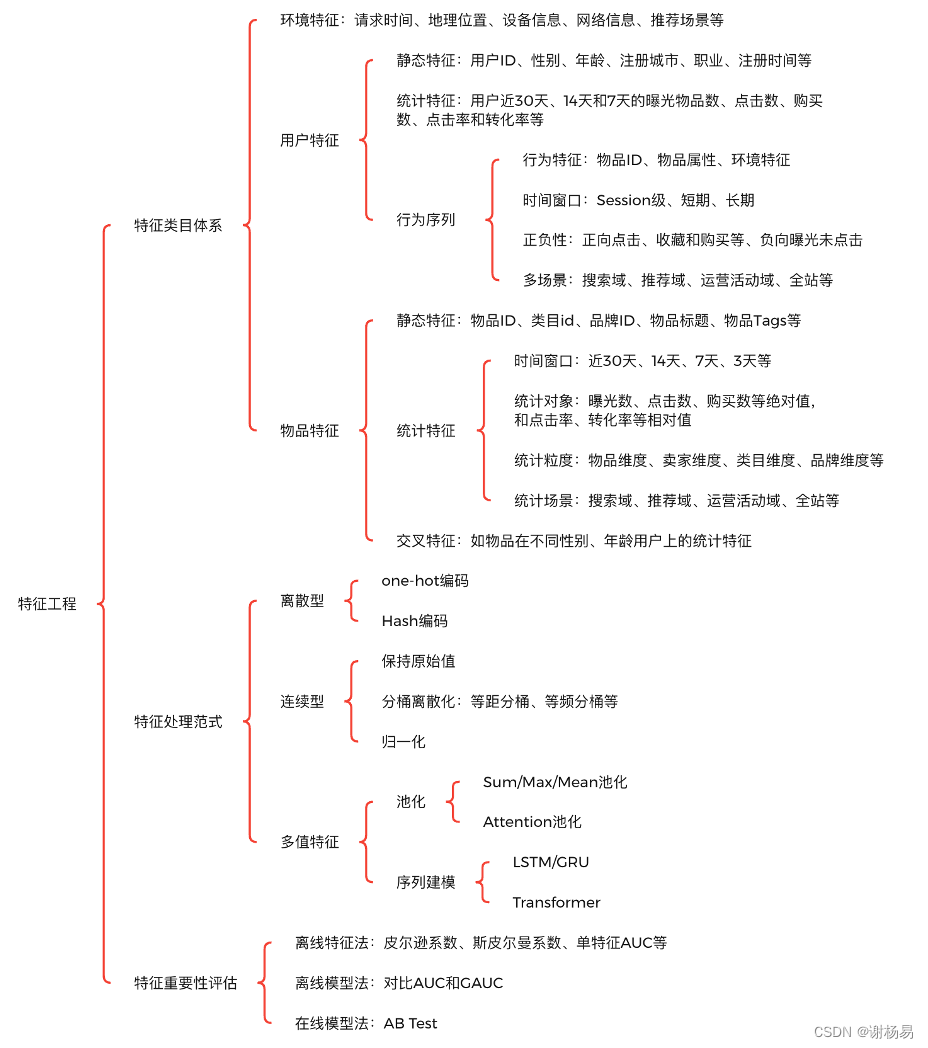
推荐算法架构7:特征工程(吊打面试官,史上最全!)
系列文章,请多关注 推荐算法架构1:召回 推荐算法架构2:粗排 推荐算法架构3:精排 推荐算法架构4:重排 推荐算法架构5:全链路专项优化 推荐算法架构6:数据样本 推荐算法架构7:特…...
Web前端 ---- 【Vue】vue路由守卫(全局前置路由守卫、全局后置路由守卫、局部路由path守卫、局部路由component守卫)
目录 前言 全局前置路由守卫 全局后置路由守卫 局部路由守卫之path守卫 局部路由守卫之component守卫 前言 本文介绍Vue2最后的知识点,关于vue的路由守卫。也就是鉴权,不是所有的组件任何人都可以访问到的,需要权限,而根据权限…...

uniapp点击tabbar之前做判断
在UniApp中,可以通过监听 tabBar 的 click 事件来在点击 tabBar 前做判断。具体步骤如下: 在 pages.json 文件中配置 tabBar,例如: {"pages":[{"path":"pages/home/home","name":"h…...
DLLNotFoundException:xxx tolua... 错误打印
DLLNotFoundException:xxx tolua... 错误打印 一、DLLNotFoundException介绍二、Plugins文件夹文件目录结构如下: 三、Plugins中的Android文件夹四、Plugins中的IOS文件夹这里不说了没测试过不过原理应该也是选择对应的平台即可五、Plugins中的x86和X86_64文件夹 一…...
Python量化投资——金融数据最佳实践: 使用qteasy+tushare搭建本地金融数据仓库并定期批量更新【附源码】
用qteasytushare实现金融数据本地化存储及访问 目的什么是qteasy什么是tushare为什么要本地化使用qteasy创建本地数据仓库qteasy支持的几种本地化仓库类型配置本地数据仓库配置tushare 的API token 配置本地数据源 —— 用MySQL数据库作为本地数据源下载金融历史数据 数据的定期…...
)
【投稿】北海 - Rust与面向对象(二)
模板方法 Rust提供了trait,类似于面向对象的接口,不同的是,将传统面向对象的虚函数表从对象中分离出来,trait仍然是一个函数表,只不过是独立的,它的参数self指针可以指向任何实现了该trait的结构。 从对象中…...
HarmonyOS构建第一个ArkTS应用(FA模型)
构建第一个ArkTS应用(FA模型) 创建ArkTS工程 若首次打开DevEco Studio,请点击Create Project创建工程。如果已经打开了一个工程,请在菜单栏选择File > New > Create Project来创建一个新工程。 选择Application应用开发&a…...
阿里云 ARMS 应用监控重磅支持 Java 21
作者:牧思 & 山猎 前言 今年的 9 月 19 日,作为最新的 LTS (Long Term Support) Java 版本,Java 21 正式 GA,带来了不少重量级的更新,详情请参考 The Arrival of Java 21 [ 1] 。虽然目前 Java 11 和 Java 17 都…...

C++ 类的析构函数和构造函数
构造函数 类的构造函数是类的一种特殊的成员函数,它会在每次创建类的新对象时执行。主要用来在创建对象时初始化对象即为对象成员变量赋初始值。 构造函数的名称与类的名称是完全相同的,并且不会返回任何类型,也不会返回 void。构造函数可用…...

STM32——CAN协议
文章目录 一.CAN协议的基本特点1.1 特点1.2 电平标准1.3 基本的五个帧1.4 数据帧 二.数据帧解析2.1 帧起始和仲裁段2.2 控制段2.3 数据段和CRC段2.4 ACK段和帧结束 三.总线仲裁四.位时序五.STM32CAN控制器原理与配置5.1 STM32CAN控制器介绍5.2 CAN的模式5.3 CAN框图 六 手册寄存…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
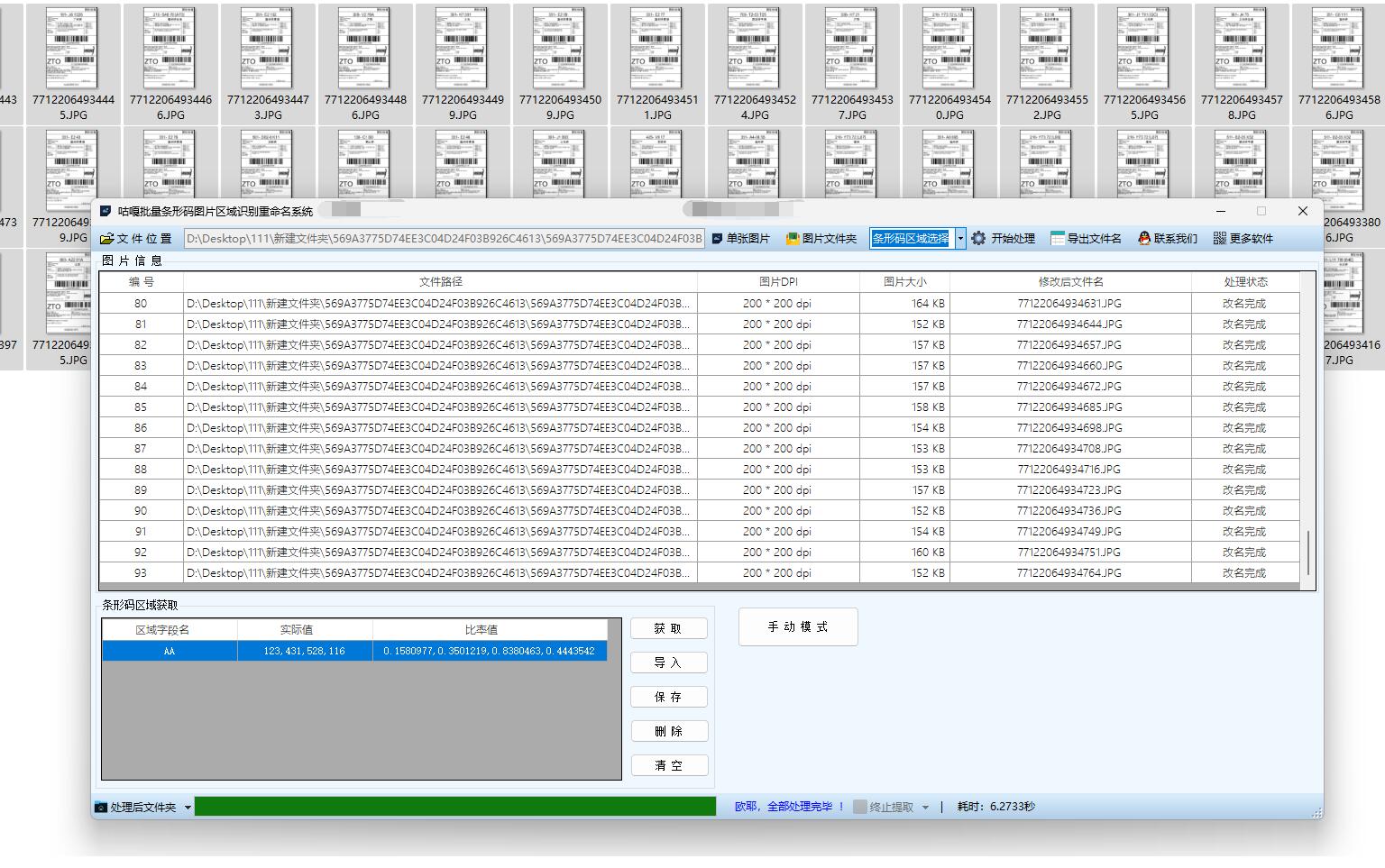
【工具教程】多个条形码识别用条码内容对图片重命名,批量PDF条形码识别后用条码内容批量改名,使用教程及注意事项
一、条形码识别改名使用教程 打开软件并选择处理模式:打开软件后,根据要处理的文件类型,选择 “图片识别模式” 或 “PDF 识别模式”。如果是处理包含条形码的 PDF 文件,就选择 “PDF 识别模式”;若是处理图片文件&…...
react更新页面数据,操作页面,双向数据绑定
// 路由不是组件的直接跳转use client,useEffect,useRouter,需3个结合, use client表示客户端 use client; import { Button,Card, Space,Tag,Table,message,Input } from antd; import { useEffect,useState } from react; impor…...

统计按位或能得到最大值的子集数目
我们先来看题目描述: 给你一个整数数组 nums ,请你找出 nums 子集 按位或 可能得到的 最大值 ,并返回按位或能得到最大值的 不同非空子集的数目 。 如果数组 a 可以由数组 b 删除一些元素(或不删除)得到,…...
