Pinely Round 3 (Div. 1 + Div. 2)(A~D)(有意思的题)
A - Distinct Buttons
题意:
思路:模拟从(0,0)到每个位置需要哪些操作,如果总共需要4种操作就输出NO。
// Problem: A. Distinct Buttons
// Contest: Codeforces - Pinely Round 3 (Div. 1 + Div. 2)
// URL: https://codeforces.com/contest/1909/problem/0
// Memory Limit: 256 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve()
{cin >> n;int flag[4] = {0 , 0 , 0 , 0};for(int i = 0 ; i < n ; i ++){int x , y;cin >> x >> y;if(x < 0){flag[0] = 1;}else if(x > 0){flag[1] = 1;}if(y < 0){flag[2] = 1;}else if(y > 0){flag[3] = 1;}} int cnt = 0;for(int i = 0 ; i < 4 ; i ++){cnt += flag[i];}if(cnt <= 3){cout <<"Yes\n";}else{cout <<"NO\n";}
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;cin>>t;while(t--){solve();}return 0;
}B - Make Almost Equal With Mod

思路:比较有意思的题目,可以发现k取2的倍数即可。证明如下:将所有数变为二进制表示,那么某个数模2的结果即二进制最后一位,模4的结果即二进制倒数第二位...如此类推。
由于题目必然存在解,也就是说数组不可能全相等。既然不可能全相等,那一定存在整个数组某一位存在1和0。因此k取2的倍数必然能够满足题意。
// Problem: B. Make Almost Equal With Mod
// Contest: Codeforces - Pinely Round 3 (Div. 1 + Div. 2)
// URL: https://codeforces.com/contest/1909/problem/B
// Memory Limit: 256 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
#define int long long
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 1e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve()
{cin >> n;int cnt1 = 0 , cnt0 = 0;for(int i = 0 ; i < n ; i++){cin >> a[i];}for(int j = 2 ; j <= llinf ; j *= 2){set<int>st;for(int i = 0 ;i < n ; i ++){st.insert(a[i] % j);}if(st.size() == 2){cout << j << endl;return;;}}}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;cin>>t;while(t--){solve();}return 0;
}
C - Heavy Intervals
题意:
思路:首先想到对l,r,c数组进行排序。可以发现,无论如何排序,所有区间长度之和是不会改变的。因此要让权值之和最小,需要让小的区间尽可能小。即对于任意而言,
为最靠近它的元素。而从小到大的处理
可以保证不会影响到后面的数。
// Problem: C. Heavy Intervals
// Contest: Codeforces - Pinely Round 3 (Div. 1 + Div. 2)
// URL: https://codeforces.com/contest/1909/problem/C
// Memory Limit: 256 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
#define int long long
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve()
{cin >> n;int l[n] , r[n] , c[n];for(int i = 0 ; i < n ; i ++)cin >> l[i];for(int i = 0 ; i < n ; i ++)cin >> r[i];for(int i = 0 ; i < n ; i ++)cin >> c[i];sort(c , c + n);sort(l , l + n);sort(r , r + n);int pre[n];stack<int>st;int ll = 0;int ans = 0;for(int i = 0 ; i < n ;i ++){while(ll < n && r[i] > l[ll]){st.push(l[ll]);ll++;}int x = st.top();st.pop();pre[i] = r[i] - x;} sort(pre , pre + n);for(int i = 0 ; i < n ; i ++){ans += pre[i] * c[n - i - 1];}cout << ans << endl;
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;cin>>t;while(t--){solve();}return 0;
}
D - Split Plus K
题意:
思路:假设最终所有数为,对于
而言,需要操作
次以后能变成ans,需要满足
。
转换一下后得到
即成立的条件为:
为了方便解释,假设所有数都大于。想要操作数最小,即
需要最大。可以发现,最终的
的最大值为
。求出gcd之后再带回原式子求出操作数
即可。相反所有数都小于
也是一样的操作。需要注意存在数等于
时,需要所有数都等于
,否则输出-1。
// Problem: D. Split Plus K
// Contest: Codeforces - Pinely Round 3 (Div. 1 + Div. 2)
// URL: https://codeforces.com/contest/1909/problem/D
// Memory Limit: 256 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
#define int long long
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve()
{// x + tk = (t + 1) * ans
// x - ans = t(ans - k)
// ans - k < 0 ??
// (x - ans / ans - k ) = t // ans 越大越好cin >> n >> m;for(int i = 0 ; i < n ; i++)cin >> a[i];sort(a.begin() , a.begin() + n);for(int i = 0 ; i < n ; i ++){if(a[0] < m && a[i] >= m){cout << -1 << endl;return;}}for(int i = 0 ; i < n ; i ++){a[i] -= m;}int ans = 0;for(int i = 0 ; i < n ; i ++){ans = gcd(ans , abs(a[i]));}int out = 0;if(a[0] == 0 && a[n - 1] != 0 || a[0] != 0 && a[n - 1] == 0){cout << -1 << endl;return;}else if(ans == 0){cout << 0 << endl;return;}for(int i = 0 ; i < n ; i ++){if(a[i] >= 0){out += (a[i] - ans) / ans ;}else{out += (a[i] + ans) / -ans;}}cout << out << endl;
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;cin>>t;while(t--){solve();}return 0;
}
相关文章:
Pinely Round 3 (Div. 1 + Div. 2)(A~D)(有意思的题)
A - Distinct Buttons 题意: 思路:模拟从(0,0)到每个位置需要哪些操作,如果总共需要4种操作就输出NO。 // Problem: A. Distinct Buttons // Contest: Codeforces - Pinely Round 3 (Div. 1 Div. 2) // URL: https…...

在Linux下探索MinIO存储服务如何远程上传文件
🌈个人主页:聆风吟 🔥系列专栏:网络奇遇记、Cpolar杂谈 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. 创建Buckets和Access Keys二. Linux 安装Cpolar三. 创建连接MinIO服务公网地…...

持续集成交付CICD:Linux 部署 Jira 9.12.1
目录 一、实验 1.环境 2.K8S master节点部署Jira 3.Jira 初始化设置 4.Jira 使用 一、实验 1.环境 (1)主机 表1 主机 主机架构版本IP备注master1K8S master节点1.20.6192.168.204.180 jenkins slave (从节点) jira9.12.1…...

Linux命令-查看内存、GC情况及jmap 用法
查看进程占用内存、CPU使用情况 1、查看进程 #jps 查看所有java进程 #top 查看cpu占用高进程 输入m :根据内存排序 topMem: 16333644k total, 9472968k used, 6860676k free, 165616k buffers Swap: 0k total, 0k used, 0k free, 6…...

nginx安装letsencrypt证书
1.安装推荐安装letsencrypt证书的客户端工具 官方推荐通过cerbot客户端安装letsencrypt 官方推荐使用snap客户端安装cerbot客户端 apt install snapd snap install --classic certbot 建立certbot软链接:ln -s /snap/bin/certbot /usr/bin/certbot 2.开始安装letse…...
docker笔记1-安装与基础命令
docker的用途: 可以把应用程序代码及运行依赖环境打包成镜像,作为交付介质,在各种环境部署。可以将镜像(image)启动成容器(container),并提供多容器的生命周期进行管理(…...
VSCode软件与SCL编程
原创 NingChao NCLib 博途工控人平时在哪里技术交流博途工控人社群 VSCode简称VSC,是Visual studio code的缩写,是由微软开发的跨平台的轻量级编辑器,支持几乎所有主流的开发语言的语法高亮、代码智能补全、插件扩展、代码对比等,…...
Opencv中的滤波器
一副图像通过滤波器得到另一张图像,其中滤波器又称为卷积核,滤波的过程称之为卷积。 这就是一个卷积的过程,通过一个卷积核得到另一张图片,明显发现新的到的图片边缘部分更加清晰了(锐化)。 上图就是一个卷…...

<JavaEE> 基于 TCP 的 Socket 通信模型
目录 一、认识相关API 1)ServerSocket 2)Socket 二、TCP字节流套接字通信模型概述 三、回显客户端-服务器 1)服务器代码 2)客户端代码 一、认识相关API 1)ServerSocket ServerSocket 常用构造方法ServerSocke…...
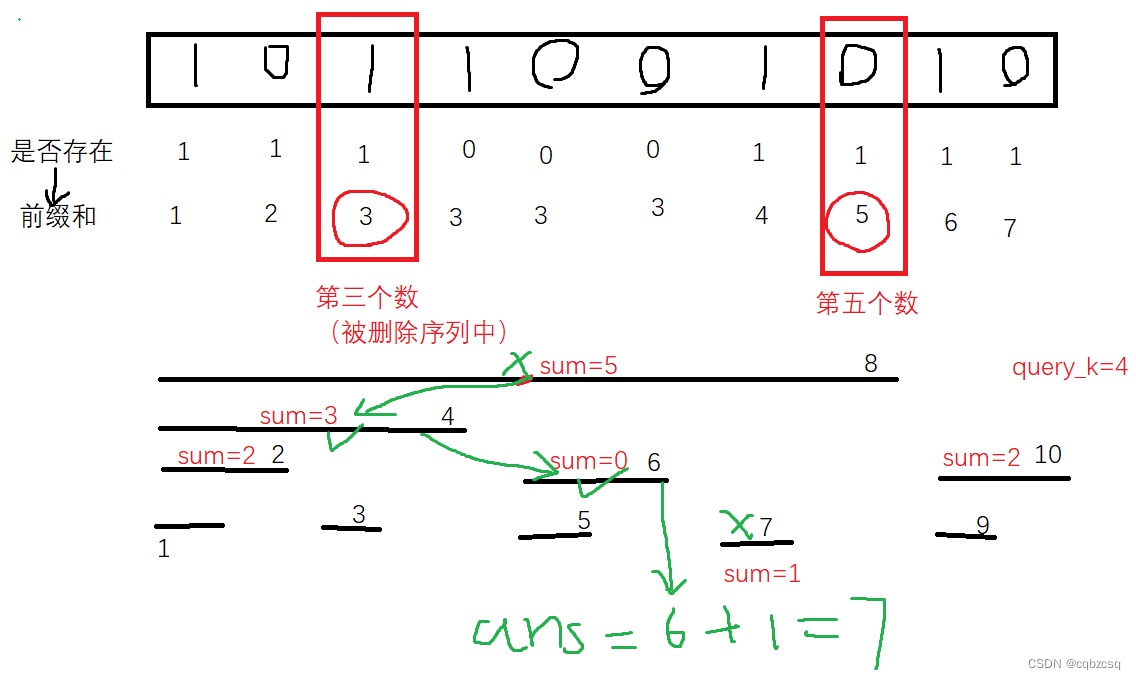
[THUPC 2024 初赛] 二进制 (树状数组单点删除+单点查询)(双堆模拟set)
题解 题目本身不难想 首先注意到所有查询的序列长度都是小于logn级别的 我们可以枚举序列长度len,然后用类似滑动窗口的方法,一次性预处理出每种字串的所有出现位置,也就是开N个set去维护所有的位置。预处理会进行O(logn)轮,每…...
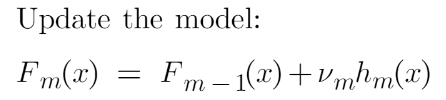
机器学习算法(11)——集成技术(Boosting——梯度提升)
一、说明 在在这篇文章中,我们学习了另一种称为梯度增强的集成技术。这是我在机器学习算法集成技术文章系列中与bagging一起介绍的一种增强技术。我还讨论了随机森林和 AdaBoost 算法。但在这里我们讨论的是梯度提升,在我们深入研究梯度提升之前…...

使用GBASE南大通用负载均衡连接池
若要使用负载均衡连接池功能,需要在连接串中配置相关的关键字。有关更详细的关键字信息在 GBASE南大通用 连接参数表‛中介绍。假设存在如下场景: 现有集群中存在 4 个节点: 192.168.9.173, 192.168.9.174, 192.168.9.175, 192.168.9.17…...
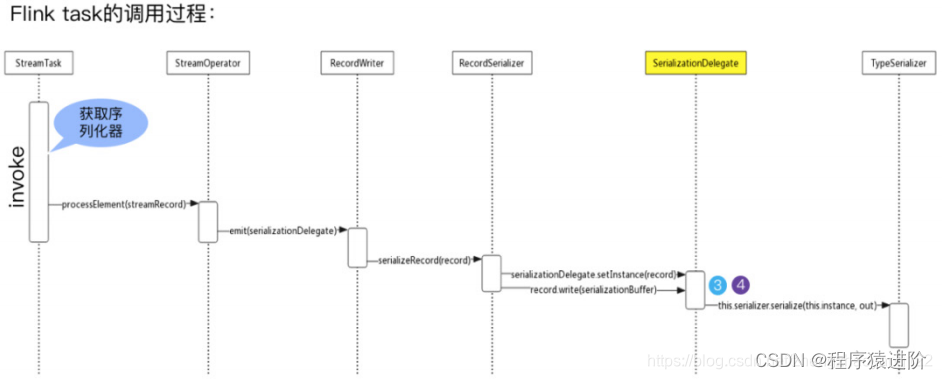
Flink 数据序列化
为 Flink 量身定制的序列化框架 大家都知道现在大数据生态非常火,大多数技术组件都是运行在JVM上的,Flink也是运行在JVM上,基于JVM的数据分析引擎都需要将大量的数据存储在内存中,这就不得不面临JVM的一些问题,比如Ja…...
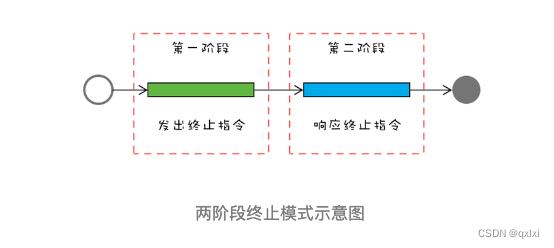
【并发设计模式】聊聊两阶段终止模式如何优雅终止线程
在软件设计中,抽象出了23种设计模式,用以解决对象的创建、组合、使用三种场景。在并发编程中,针对线程的操作,也抽象出对应的并发设计模式。 两阶段终止模式- 优雅停止线程避免共享的设计模式- 只读、Copy-on-write、Thread-Spec…...
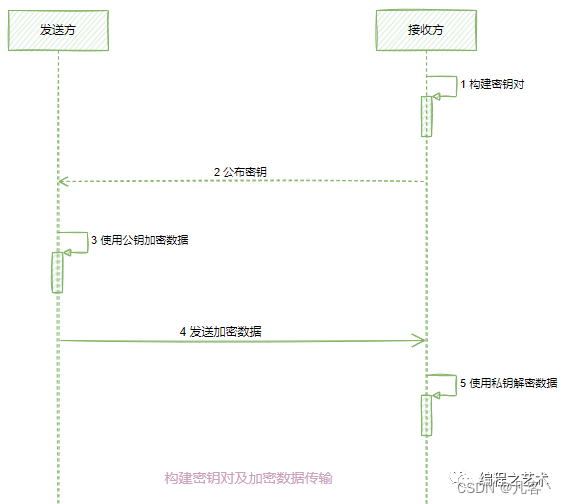
Java实现非对称加密【详解】
Java实现非对称加密 1. 简介2. 非对称加密算法--DH(密钥交换)3. 非对称加密算法--RSA非对称加密算法--EIGamal5. 总结6 案例6.1 案例16.2 案例2 1. 简介 公开密钥密码学(英语:Public-key cryptography)也称非对称式密…...

simulinkveristandlabview联合仿真——模型导入搭建人机界面
目录 1.软件版本 2.搭建simulink仿真模型 编译错误 3.导入veristand并建立工程 4.veristand导入labview labview显示veristand工程数据 labview设置veristand工程数据 运行labview工程 1.软件版本 matlab2020a,veristand2020 R4,labview2020 SP…...
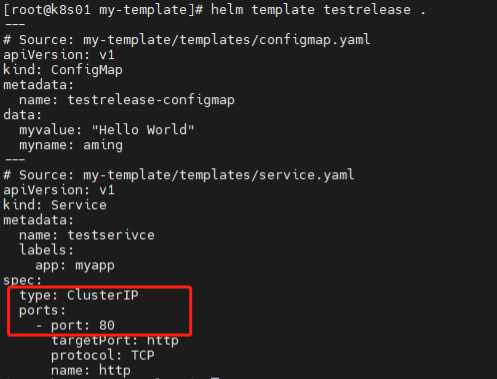
k8s中Helm工具实践
k8s中Helm工具实践 1)安装redis-cluster 先搭建一个NFS的SC(只需要SC,不需要pvc),具体步骤此文档不再提供,请参考前面相关章节。 下载redis-cluster的chart包 helm pull bitnami/redis-cluster --untar…...
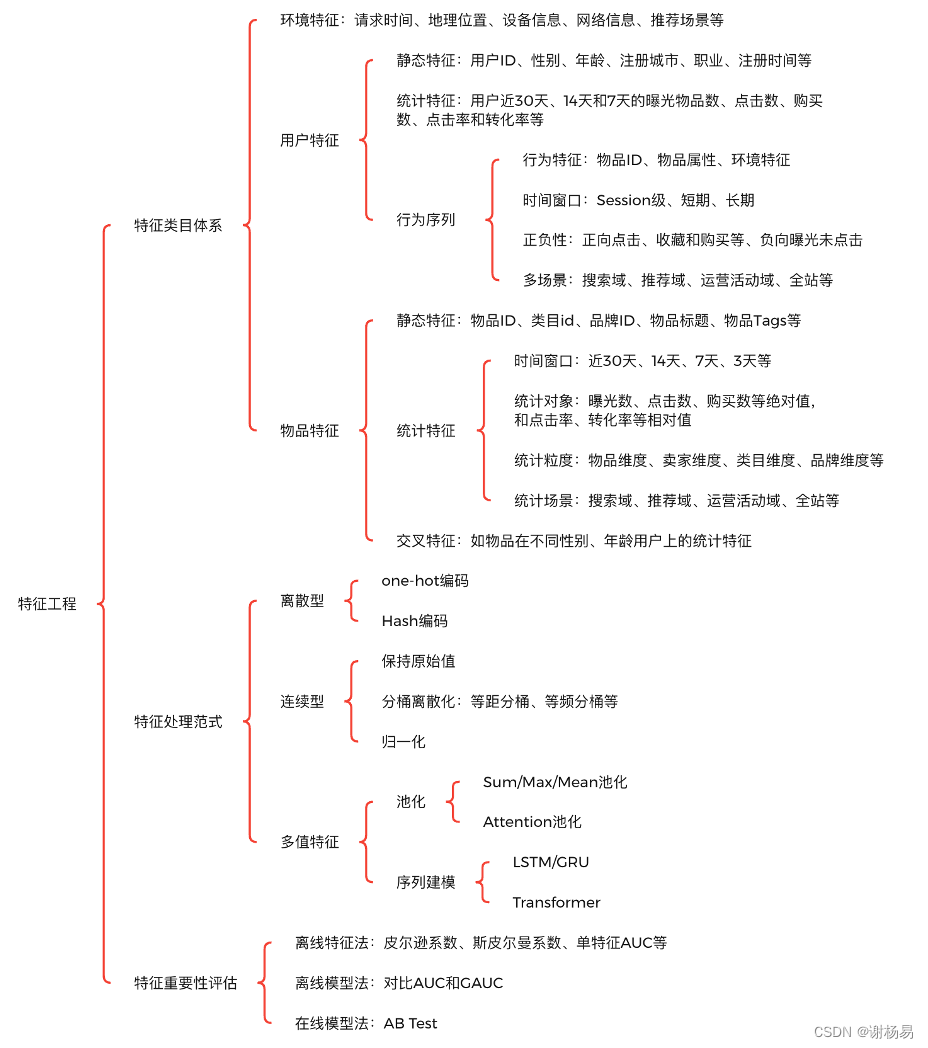
推荐算法架构7:特征工程(吊打面试官,史上最全!)
系列文章,请多关注 推荐算法架构1:召回 推荐算法架构2:粗排 推荐算法架构3:精排 推荐算法架构4:重排 推荐算法架构5:全链路专项优化 推荐算法架构6:数据样本 推荐算法架构7:特…...
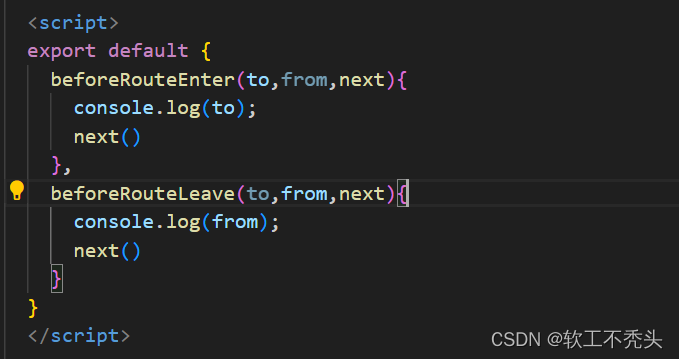
Web前端 ---- 【Vue】vue路由守卫(全局前置路由守卫、全局后置路由守卫、局部路由path守卫、局部路由component守卫)
目录 前言 全局前置路由守卫 全局后置路由守卫 局部路由守卫之path守卫 局部路由守卫之component守卫 前言 本文介绍Vue2最后的知识点,关于vue的路由守卫。也就是鉴权,不是所有的组件任何人都可以访问到的,需要权限,而根据权限…...

uniapp点击tabbar之前做判断
在UniApp中,可以通过监听 tabBar 的 click 事件来在点击 tabBar 前做判断。具体步骤如下: 在 pages.json 文件中配置 tabBar,例如: {"pages":[{"path":"pages/home/home","name":"h…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
