【计算机视觉中的多视图几何系列】深入浅出理解针孔相机模型
温故而知新,可以为师矣!
一、参考资料
《计算机视觉中的多视图几何-第五章》-Richard Hartley, Andrew Zisserman.
二、针孔模型相关介绍
1. 重要概念

1.1 投影中心/摄像机中心/光心
投影中心称为摄像机中心,也称为光心。投影中心位于一个欧式坐标系的原点。
1.2 图像平面/聚焦平面
平面 Z = f Z=f Z=f 被称为图像平面或聚焦平面。
1.3 主轴/主射线
摄像机中心到图像平面的垂线称为摄像机的主轴或主射线。
1.4 主点
主轴与图像平面的交点称为主点。
1.5 主平面(摄像机)
过摄像机中心平行于图像平面的平面称为摄像机的主平面。
2. 摄像机投影
从3维世界降到2维图像是一个投影过程,在此过程中我们失去了一维。建模这个过程的常用方式是利用中心投影,由空间中的一个点引出一条从3D世界点到空间中的一个固定点(投影中心)的射线,这条射线将与空间中被选为图像平面的具体平面相交。射线与图像平面的交点表示该点的图像。

在针孔摄像机模型下,3维空间坐标为 X = ( X , Y , Z ) T X=(X, Y, Z)^T X=(X,Y,Z)T 的点 X X X 被投影到图像平面上的一点,该点是连接点 X X X 与投影中心的直线与图像平面的交点。根据相似三角形,可以很快地算出点 ( X , Y , Z ) T (X, Y , Z)^T (X,Y,Z)T 被映射到图像平面上点 ( f X / Z , f Y / Z , f ) T (fX/Z, fY/Z, f)^T (fX/Z,fY/Z,f)T 。略去最后一个图像坐标之后,从世界坐标到图像坐标的中心投影是:
( X , Y , Z ) T ↦ ( f X / Z , f Y / Z ) T ( 1 ) (X,Y,Z)^{T}\mapsto(fX/Z,fY/Z)^{T}\quad(1) (X,Y,Z)T↦(fX/Z,fY/Z)T(1)
这是从3维欧式空间 IR 3 \text{IR}^3 IR3 到 2维欧式空间 IR 2 \text{IR}^2 IR2 的一个映射。
3. 投影矩阵
齐次坐标的概念:齐次坐标就是用N+1维去描述一个N维的坐标。
如果用齐次矢量表示世界和图像点,那么中心投影可以简单地表示成齐次坐标之间的线性映射。具体地说, 公式 ( 1 ) 公式(1) 公式(1) 可以写成如下矩阵乘积形式:
[ X Y Z 1 ] ↦ [ f x f y z ] = [ f 0 f 0 1 0 ] [ X Y Z 1 ] ( 2 ) \left.\left[\begin{array}{c}\mathbf{X}\\\mathbf{Y}\\\mathbf{Z}\\\mathbf{1}\end{array}\right.\right]\mapsto\left[\begin{array}{c}f\mathbf{x}\\f\mathbf{y}\\\mathbf{z}\end{array}\right]=\left[\begin{array}{cc}f&&&0\\&f&&0\\&&1&0\end{array}\right]\left[\begin{array}{c}\mathbf{X}\\\mathbf{Y}\\\mathbf{Z}\\\mathbf{1}\end{array}\right]\quad(2) XYZ1 ↦ fxfyz = ff1000 XYZ1 (2)
其中 [ f 0 f 0 1 0 ] \left[\begin{array}{cc}f&&&0\\&f&&0\\&&1&0\end{array}\right] ff1000 表示 3 ∗ 4 3*4 3∗4 齐次摄像机投影矩阵,记作 P P P。 P P P 可以写成 d i a g ( f , f , 1 ) [ I ∣ 0 ] diag(f,f,1)[I|0] diag(f,f,1)[I∣0],其中 d i a g ( f , f , 1 ) diag(f,f,1) diag(f,f,1)是对角矩阵,而 [ I ∣ 0 ] [I|0] [I∣0]表示矩阵分块成一个 3 ∗ 3 3*3 3∗3 恒等矩阵加上一个零列矢量。那么,中心投影的针孔模型的摄像机投影矩阵可以表示为:
P = d i a g ( f , f , 1 ) [ I ∣ 0 ] P=diag(f,f,1)[I|0] P=diag(f,f,1)[I∣0]
恒等矩阵的概念:恒等矩阵,又称为单位矩阵,是一个方阵,其对角线上的元素为1,其余元素均为0,记作 I I I或者 E E E。恒等矩阵的大小由其维度决定,例如3阶恒等矩阵是一个3x3的矩阵。
恒等矩阵在线性代数中具有很多重要的性质。例如,对于任意矩阵A,恒等矩阵1与A的乘积等于A本身。这是因为恒等矩阵的每个元素与A的对应元素相乘,并将其相加,得到的结果就是A本身。这个性质在矩阵的转置、逆运算等方面都有着重要的应用。
恒等矩阵在深度学习中也具有重要的作用。在神经网络中,恒等矩阵常被用作初始化权重矩阵。初始化权重矩阵时,将其设置为恒等矩阵可以使得神经网络的初始状态更稳定。这是因为恒等矩阵具有一定的对称性和平衡性,可以避免梯度消失或梯度爆炸等问题,有助于提高模型的训练效果。
恒等矩阵还可以用于矩阵的相似性度量。在图像处理和模式识别中,我们经常需要比较两个矩阵的相似性。通过计算两个矩阵之间的差异,可以得到它们的相似性度量。而恒等矩阵作为一个特殊的矩阵,与其他矩阵相比具有明显的差异,可以用于度量矩阵之间的相似性。
我们现在引入如下记号:世界点 X X X 用4维齐次矢量 ( X , Y , Z , 1 ) (X,Y,Z,1) (X,Y,Z,1)表示;图像点 x x x 被表示成3维齐次矢量的形式。则 公式 ( 2 ) 公式(2) 公式(2) 可以紧凑地写为:
x = P X x=PX x=PX
4. 主点偏置
公式 ( 1 ) 公式(1) 公式(1) 假定图像平面的坐标原点在主点上。实际情况可能不是这样,如下图所示:

摄像机坐标系 ( x c a m , y c a m ) T (x_{cam},y_{cam})^T (xcam,ycam)T的坐标原点为摄像机中心,该原点在图像平面的投影是主点p。图像坐标系 ( x , y ) T (x,y)^T (x,y)T 的坐标原点为图像的左下角。
因此一般情形的映射为:
( X , Y , Z ) T ↦ ( f X / Z + p x , f Y / Z + p y ) T (X,Y,Z)^{T}\mapsto(fX/Z+p_x,fY/Z+p_y)^{T} \\ (X,Y,Z)T↦(fX/Z+px,fY/Z+py)T
其中 ( p x , p y ) T (p_x,p_y)^T (px,py)T 是主点的坐标。该方程用齐次坐标可以表示为:
[ X Y Z 1 ] ↦ [ f x + Z p x f y + Z p y z ] = [ f p x 0 f p x 0 1 0 ] [ X Y Z 1 ] ( 3 ) \left.\left[\begin{array}{c}\mathbf{X}\\\mathbf{Y}\\\mathbf{Z}\\\mathbf{1}\end{array}\right.\right]\mapsto\left[\begin{array}{c}f\mathbf{x+Zp_x}\\f\mathbf{y+Zp_y}\\\mathbf{z}\end{array}\right]=\left[\begin{array}{cc}f&&p_x&0\\&f&p_x&0\\&&1&0\end{array}\right]\left[\begin{array}{c}\mathbf{X}\\\mathbf{Y}\\\mathbf{Z}\\\mathbf{1}\end{array}\right]\quad(3) XYZ1 ↦ fx+Zpxfy+Zpyz = ffpxpx1000 XYZ1 (3)
若记
K = [ f p x f p x 1 ] ( 4 ) K=\left[\begin{array}{cc}f&&p_x\\&f&p_x\\&&1\end{array}\right]\quad(4) K= ffpxpx1 (4)
则 公式 ( 3 ) 公式(3) 公式(3) 有一个简洁的形式:
x = K [ I ∣ 0 ] X c a m ( 5 ) x=K[I|0]X_{cam}\quad(5) x=K[I∣0]Xcam(5)
矩阵 K K K 称为摄像机标定矩阵,在 公式 ( 5 ) 公式(5) 公式(5) 中我们记 ( X , Y , Z , 1 ) T (X,Y,Z,1)^T (X,Y,Z,1)T 为 X c a m X_{cam} Xcam 是为了强调摄像机被设定在一个欧式坐标系的原点且主轴沿着 z z z 轴的指向,而点 X c a m X_{cam} Xcam 按此坐标系表示。这样的坐标系可以称为摄像机坐标系。
摄像机坐标系的原点为摄像机中心, z z z轴方向指向主轴。
5. 摄像机旋转与位移
一般,3维空间点采用不同的欧式坐标系表示,称为世界坐标系。摄像机坐标系与世界坐标系通过旋转和平移相联系。

如果 X ~ \widetilde{X} X 是一个3维非齐次矢量,表示世界坐标系中一点的坐标,而 X ~ c a m \widetilde{X}_{cam} X cam 是以摄像机坐标系来表示的同一点,那么我们可以记 X ~ c a m = R ( X ~ − C ~ ) \widetilde{X}_{cam}=R\left(\widetilde{X}-\widetilde{C}\right) X cam=R(X −C ) ,其中 C ~ \widetilde{C} C 表示摄像机中心在世界坐标系中的坐标, R R R 是一个 3 ∗ 3 3*3 3∗3 的旋转矩阵,表示摄像机坐标系的方位。这个方程在齐次坐标系下可以写成:
X c a m = [ R − R C ~ 0 T 1 ] [ X Y Z 1 ] = [ R − R C ~ 0 T 1 ] X ( 6 ) X_{cam}=\begin{bmatrix}R&-R\widetilde{C}\\0^{T}&1\end{bmatrix}\begin{bmatrix}X\\Y\\Z\\1\end{bmatrix}=\begin{bmatrix}R&-R\widetilde{C}\\0^{T}&1\end{bmatrix}\mathbf{X}\quad(6) Xcam=[R0T−RC 1] XYZ1 =[R0T−RC 1]X(6)
把它与 公式 ( 5 ) 公式(5) 公式(5) 结合起来形成公式:
x = K R [ I ∣ − C ~ ] X ( 7 ) x=KR\left[I|-\widetilde{C}\right]X\quad(7) x=KR[I∣−C ]X(7)
其中 X X X 用世界坐标系表示。这是由一个针孔模型给出的一般映射。
6. 摄像机内部参数与外部参数
由 公式 ( 7 ) 公式(7) 公式(7) 可以看出,一般的针孔摄像机 P = K R [ I ∣ − C ~ ] P=KR\left[I|-\widetilde{C}\right] P=KR[I∣−C ] 有9个自由度:3个来自 K (元素 f , p x , p y ) K(元素 f,p_x, p_y) K(元素f,px,py),3个来自 R R R,3个来自 C ~ \widetilde{C} C 。包含在 K K K 中的参数称为摄像机内部参数或摄像机的内部校准。包含在 R R R 和 C ~ \widetilde{C} C 中的参数与摄像机在世界坐标系中的方位和位置有关,并称为外部参数或外部校准。
为方便起见,通常摄像机中心不明显标出,而把世界坐标系到图像坐标系的变换表示成 X ~ c a m = R X ~ + t \widetilde{X}_{cam}=R\widetilde{X}+t X cam=RX +t。在次情形时摄像机矩阵简化成:
P = k [ R ∣ t ] ( 8 ) P=k[R|t]\quad(8) P=k[R∣t](8)
其中根据 公式 ( 7 ) 公式(7) 公式(7) , t = − R C ~ t=-R\widetilde{C} t=−RC 。
7. CCD摄像机
对于基本针孔模型,假定图像坐标在两个轴向上有等尺度的欧式坐标。但CCD摄像机的像素可能不是正方形。如果图像坐标以像素来测量,那么需要在每个方向上引入非等量尺度因子。具体地说,如果在 x x x 和 y y y 方向上图像坐标单位距离的像素数分别是 m x m_x mx 和 m y m_y my,那么由世界坐标到像素坐标的变换由 公式 ( 4 ) 公式(4) 公式(4) 左乘一个附加的因子 d i a g ( m x , m y , 1 ) diag(m_x,m_y,1) diag(mx,my,1) 而得到。因此一个CCD摄像机标定矩阵的一般形式是:
K = [ a x x 0 a y y 0 1 ] ( 9 ) K=\left[\begin{array}{cc}a_x&&x_0\\&a_y&y_0\\&&1\end{array}\right]\quad(9) K= axayx0y01 (9)
其中 a x = f m x a_x=fm_x ax=fmx 和 a y = f m y a_y=fm_y ay=fmy 分别把摄像机的焦距换算成 x x x 和 y y y 方向的像素量纲。同理, x ~ 0 = ( x 0 , y 0 ) T \widetilde{x}_0=(x_0,y_0)^T x 0=(x0,y0)T 是用像素量纲表示的主点,它的坐标是 x 0 = m x p x x_0=m_xp_x x0=mxpx 和 y 0 = m y p y y_0=m_yp_y y0=mypy。因此,一个CCD摄像机有10个自由度。
相关文章:

【计算机视觉中的多视图几何系列】深入浅出理解针孔相机模型
温故而知新,可以为师矣! 一、参考资料 《计算机视觉中的多视图几何-第五章》-Richard Hartley, Andrew Zisserman. 二、针孔模型相关介绍 1. 重要概念 1.1 投影中心/摄像机中心/光心 投影中心称为摄像机中心,也称为光心。投影中心位于一…...
——函数)
轻量级Python IDE使用(三)——函数
1、函数 1.1、函数的概述 在程序设计中,函数的使用可以提升代码的复用率和可维护性。 系统内建函数pow()进行幂运算: a pow(2,4)自定义函数func() def func(a,b):return a ** b afunc(2,4) print(a)自定义函数func(),功能是输出a的b次幂 1.2、函数的定义 py…...
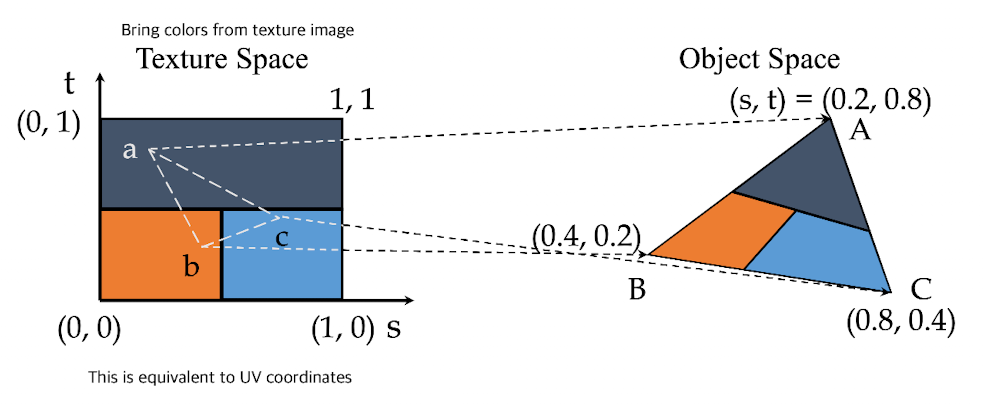
计算机图形学理论(3):着色器编程
本系列根据国外一个图形小哥的讲解为本,整合互联网的一些资料,结合自己的一些理解。 CPU vs GPU CPU支持: 快速缓存分支适应性高性能 GPU支持: 多个 ALU快速板载内存并行任务的高吞吐量(在每个片段、顶点上执行着色…...
ubuntu20.04安装timeshift最新方法
总结: 现在可以使用如下代码安装 sudo apt-get update sudo apt-get install timeshift原因: 在尝试Timeshift系统备份与还原中的方法时, sudo apt-add-repository -y ppa:teejee2008/ppa运行失败。 更改为以下代码: sudo a…...
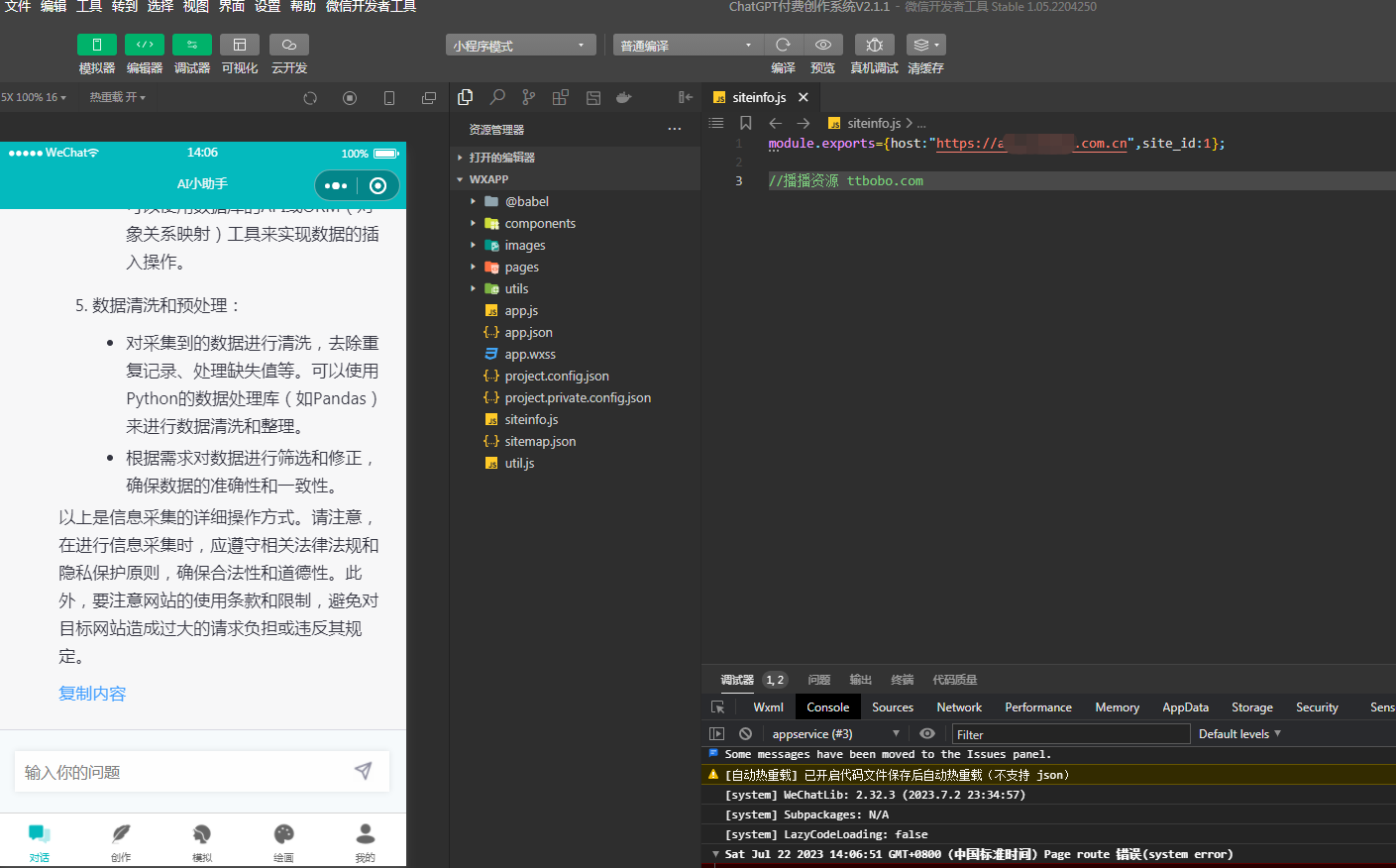
小狐狸ChatGPT付费创作系统小程序端开发工具提示打开显示无法打开页面解决办法
最新版2.6.7版下载:https://download.csdn.net/download/mo3408/88656497 很多会员在上传小程序前端时经常出现首页无法打开的情况,错误提示无法打开该页面,不支持打开,这种问题其实就是权限问题,页面是通过调用web-v…...
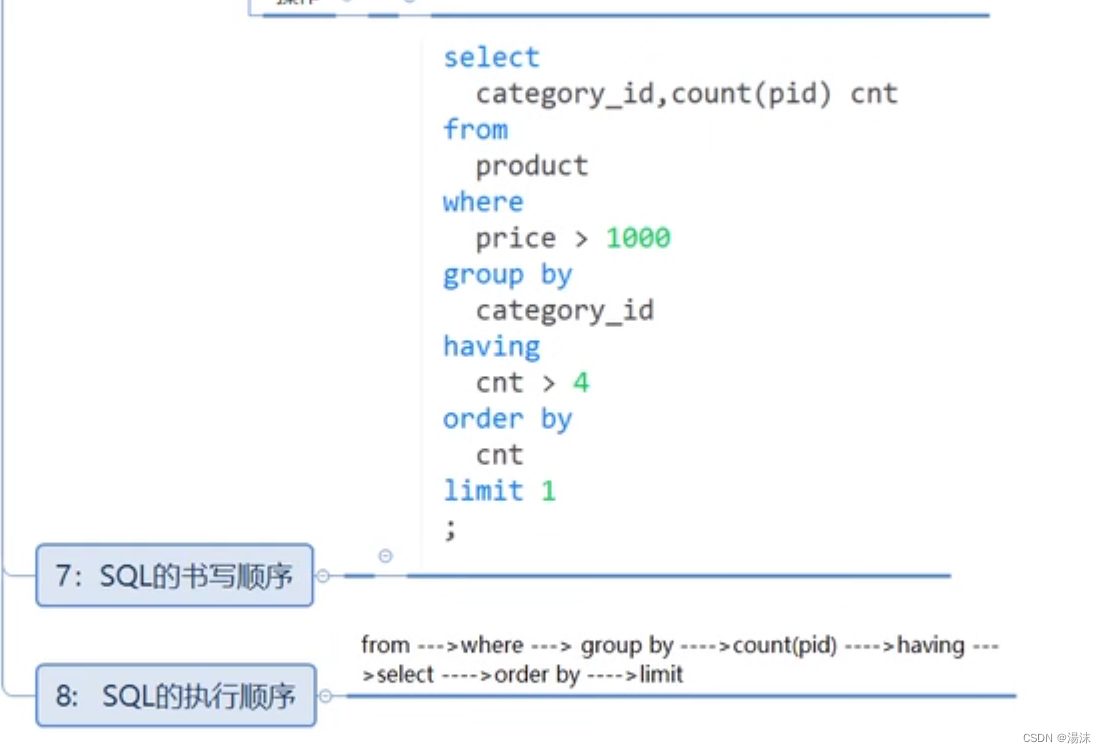
DQL-基本查询
概念: 1,数据库管理系统一个重要功能就是数据查询,数据查询不应只是简单返回数据库中存储的数据,还应该根据需要对数据进行筛选以及确定数据以什么样的格式显示 2,MySQL提供了功能强大、灵活的语句来实现这些操作 3…...
漏洞复现-红帆OA iorepsavexml.aspx文件上传漏洞(附漏洞检测脚本)
免责声明 文章中涉及的漏洞均已修复,敏感信息均已做打码处理,文章仅做经验分享用途,切勿当真,未授权的攻击属于非法行为!文章中敏感信息均已做多层打马处理。传播、利用本文章所提供的信息而造成的任何直接或者间接的…...

Leetcode 2976. Minimum Cost to Convert String I
Leetcode 2976. Minimum Cost to Convert String I 1. 解题思路2. 代码实现 题目链接:2976. Minimum Cost to Convert String I 1. 解题思路 这道题思路上其实是非常直接的,本质上就是给出有向图之后,求出有向图上任意两点之间的最短距离&…...

ZKP Mathematical Building Blocks (2)
MIT IAP 2023 Modern Zero Knowledge Cryptography课程笔记 Lecture 3: Mathematical Building Blocks (Yufei Zhao) Fiat Shamir heuristic Turn an interactive proof to a non-interactive proofP can simulate V whenever V picks a random valueP can simulate V’s ran…...
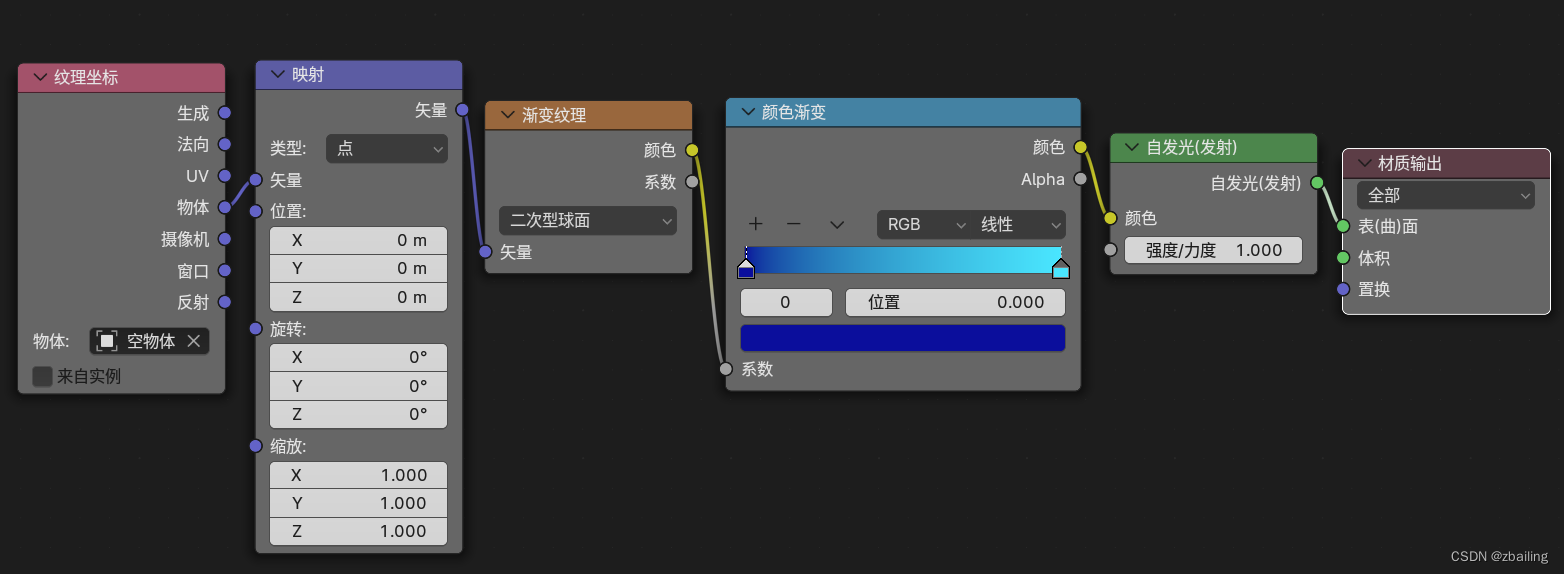
blender径向渐变材质-着色编辑器
要点: 1、用纹理坐标中的物体输出连接映射中的矢量输入 2、物体选择一个空坐标,将空坐标延z轴上移一段距离 3、空坐标的大小要缩放到和要添加材质的物体大小保持一致...

2023美团机器人研究院学术年会成功举办
2023年12月19日,深圳市美团机器人研究院学术年会在清华大学深圳国际研究生院成功落下帷幕。会议回顾了研究院成立一年来的进展和成果,并邀请了各界专家共同讨论机器人技术的未来发展趋势。此外,年会期间还举办了首届低空经济智能飞行管理挑战…...

swing快速入门(二十七)
注释很详细,直接上代码 上一篇 新增内容 1.为按钮指定图标 2. 列表框的并列 3.菜单项绑定快捷键 4.控件悬浮提示信息 5.菜单项设置小图标 6.五种布局风格右键选择切换 package swing21_30;import javax.swing.*; import java.awt.*; import java.awt.event.…...
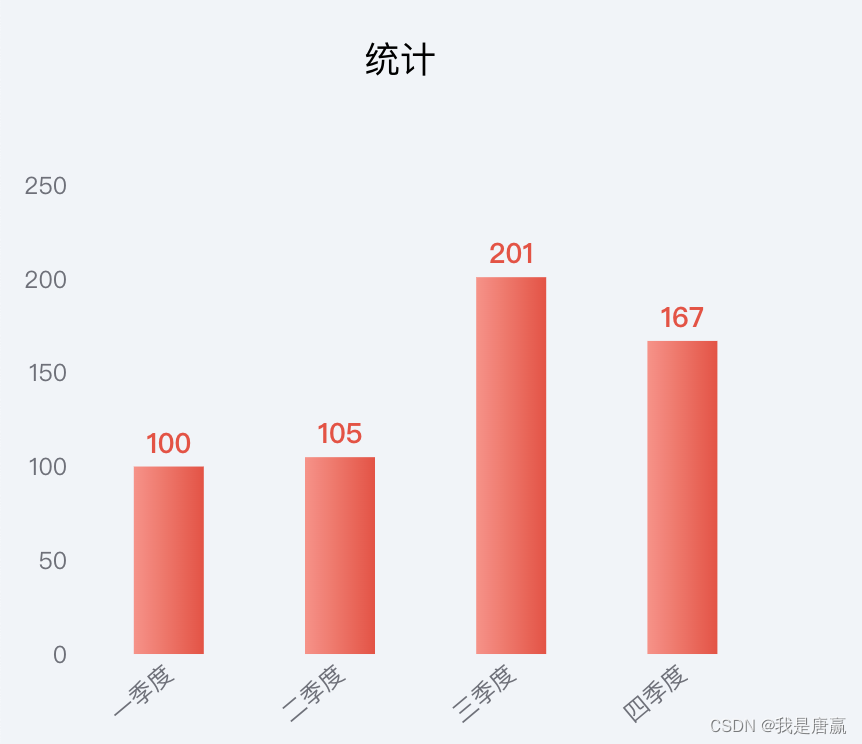
Vue 封装echarts柱状图(Bar)组件
目的:减少重复代码,便于维护 显示效果 组件代码 <template><div class"ldw-data-content-box"><div class"ldw-chilren-box"><div class"title" v-if"title">{{ title }}</div>…...
)
异常(Java)
1.异常的概念 在 Java 中,将程序执行过程中发生的不正常行为称为异常 。 1.算数异常 System.out.println(10 / 0); // 执行结果 Exception in thread "main" java.lang.ArithmeticException: / by zero 2.数组越界异常 int[] arr {1, 2, 3}; System.out.…...

vue的插槽解析
插槽 好处:组件的内容结构可定制 用slot插槽进行占位 语法: 子组件中通过slot进行占位 理解:父组件,在子组件标签嵌套的内容就会被渲染到slot地方 一、默认插槽 //子组件 <slot>slot插槽</slot> //方法一<slot name"…...
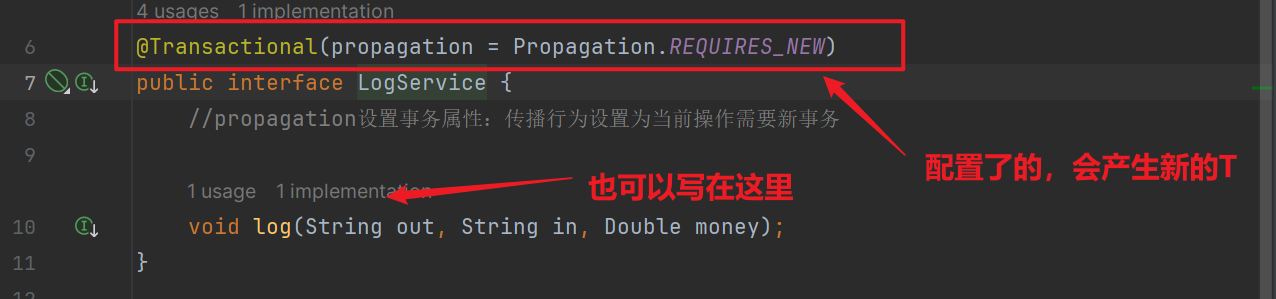
Spring(3)Spring从零到入门 - Spring整合技术及AOP事务管理
Spring(3)Spring从零到入门 - Spring整合技术及AOP事务管理 文章目录 Spring(3)Spring从零到入门 - Spring整合技术及AOP事务管理4 Spring整合技术示例4.1 Spring整合Mybatis4.1.1 Mybatis开发回顾4.1.2 整合Spring分析4.1.3 Spri…...

适配器模式学习
适配器模式(Adapter)将一个类的接口转换成客户希望的另外一个接口。Adapter 模式使得原本由于接口不兼容而不能一起工作的那些类可以一起工作。 适配器模式分为类适配器模式和对象适配器模式两种,前者类之间的耦合度比后者高,且要…...
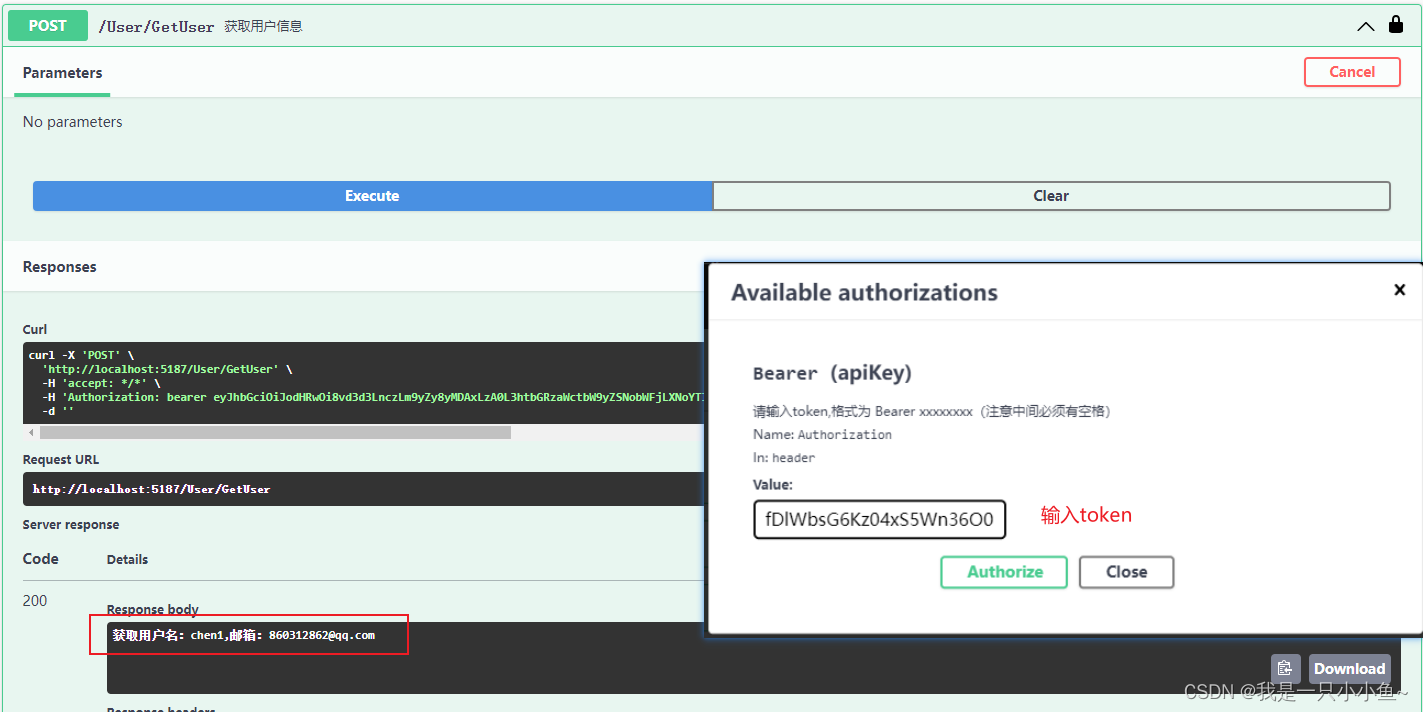
NET中使用Identity+CodeFirst+Jwt实现登录、鉴权
目录 前言 一、创建上下文类 1.自定义MyContext上下文类继承IdentityDbContext 2.在Program中添加AddDbContext服务 二、使用Migration数据迁移 1.在控制台中 依次使用add-migration 、updatebase 命令 2.如何修改表名 3.如何自定义字段 三、使用Identity实现登录、修改密码 …...

详解Keras3.0 API: Optimizers
Optimizers 优化器(Optimizer)是深度学习中用于更新模型参数的一种方法,它的目标是最小化损失函数。在训练神经网络时,我们通常使用梯度下降法来更新参数,而优化器就是实现这一过程的工具。优化器的主要作用是在每次迭…...

【数据结构】字符串匹配|BF算法|KMP算法|next数组的优化
字符串匹配算法是在实际工程中经常遇到的问题,也是各大公司笔试面试的常考题目,本文主要介绍BF算法(最好想到的算法,也最好实现)和KMP算法(最经典的) 一、BF算法 BF算法,即暴力(Bru…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...
